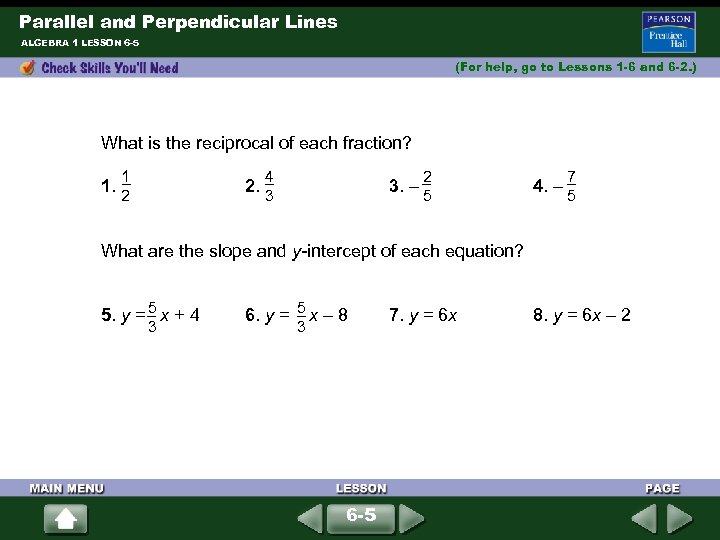
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 (For help, go to Lessons 1 -6 and 6 -2. ) What is the reciprocal of each fraction? 1. 1 2 2. 4 3 3. – 2 5 4. – 7 5 What are the slope and y-intercept of each equation? 5 5. y = x + 4 3 5 6. y = x – 8 3 6 -5 7. y = 6 x 8. y = 6 x – 2
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 Solutions 1 2 1. The reciprocal of is or 2. 4 3 2. The reciprocal of is . 2 5 3. The reciprocal of – is – . 7 5 4. The reciprocal of – is – . 5 5. y = x + 4 5 6. y = x – 8 2 1 5 3 2 4 5 3 3 5 slope: 3 5 y-intercept: 4 slope: 3 y-intercept: – 8 7. y = 6 x slope: 6 y-intercept: 0 8. y = 6 x – 2 slope: 6 y-intercept: – 2 6 -5 7
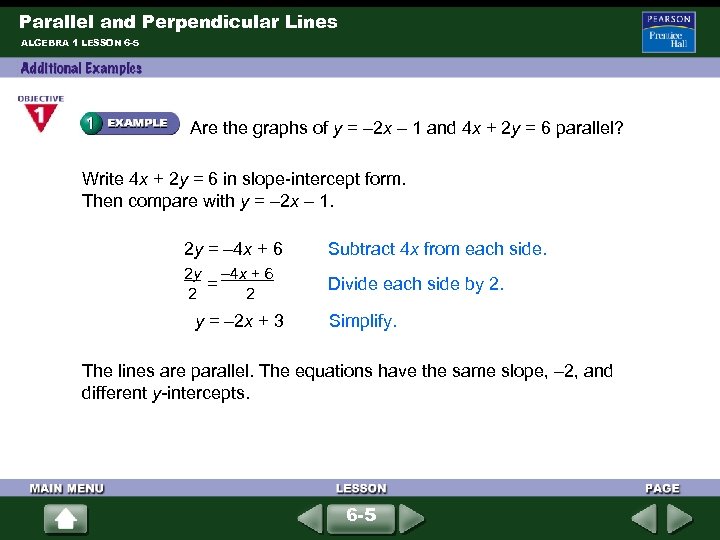
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 Are the graphs of y = – 2 x – 1 and 4 x + 2 y = 6 parallel? Write 4 x + 2 y = 6 in slope-intercept form. Then compare with y = – 2 x – 1. 2 y = – 4 x + 6 2 y – 4 x + 6 = Divide each side by 2. y = – 2 x + 3 Simplify. 2 2 Subtract 4 x from each side. The lines are parallel. The equations have the same slope, – 2, and different y-intercepts. 6 -5
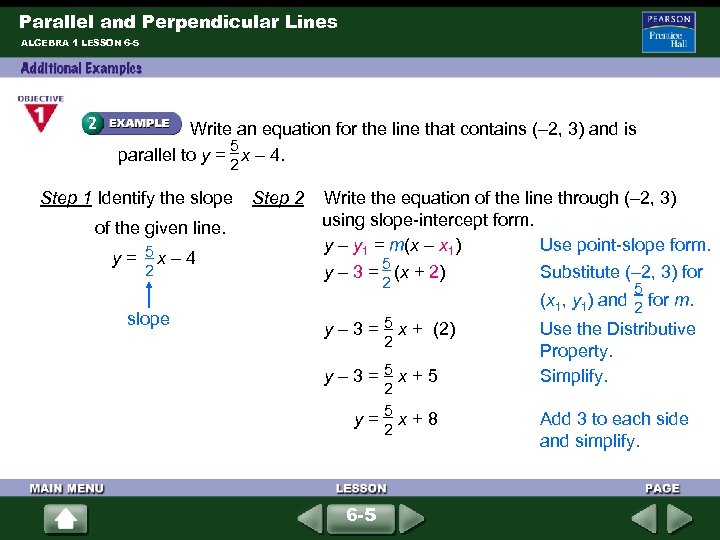
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 Write an equation for the line that contains (– 2, 3) and is 5 parallel to y = x – 4. 2 Step 2 Write the equation of the line through (– 2, 3) Step 1 Identify the slope of the given line. using slope-intercept form. y – y 1 = m(x – x 1) Use point-slope form. 5 y = x – 4 5 2 y – 3 = (x + 2) Substitute (– 2, 3) for 2 5 (x 1, y 1) and for m. 2 slope 5 y – 3 = x + (2) Use the Distributive 2 Property. 5 y – 3 = x + 5 Simplify. 2 5 y = x + 8 2 6 -5 Add 3 to each side and simplify.
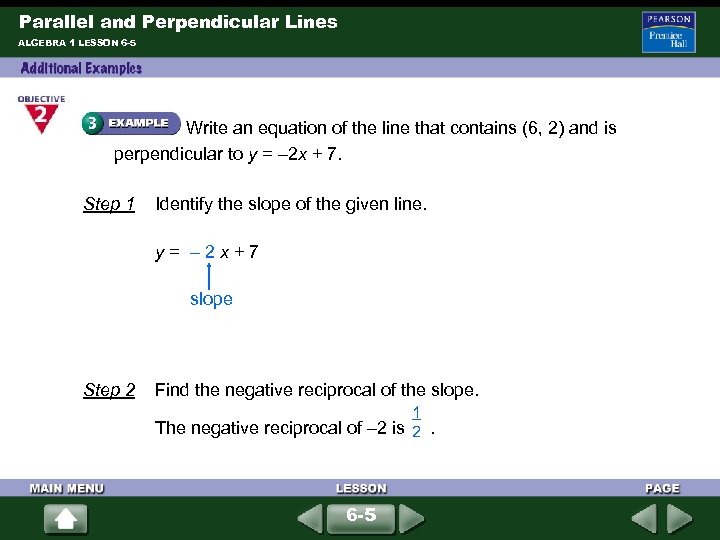
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 Write an equation of the line that contains (6, 2) and is perpendicular to y = – 2 x + 7. Step 1 Identify the slope of the given line. y = – 2 x + 7 slope Step 2 Find the negative reciprocal of the slope. 1 The negative reciprocal of – 2 is . 2 6 -5
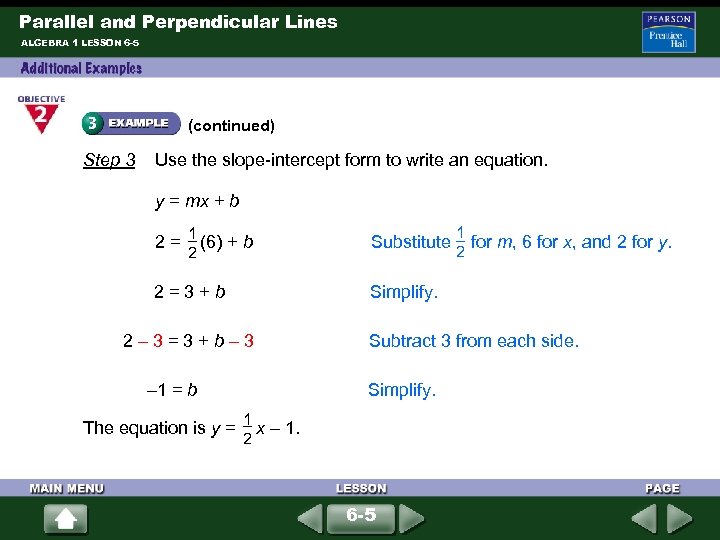
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 (continued) Step 3 Use the slope-intercept form to write an equation. y = mx + b 1 2 = (6) + b Substitute for m, 6 for x, and 2 for y. 2 2 = 3 + b Simplify. 2 – 3 = 3 + b – 3 – 1 = b Subtract 3 from each side. Simplify. 1 2 The equation is y = x – 1. 6 -5
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 The line in the graph represents the street in front of a new house. The point is the front door. The sidewalk from the front door will be perpendicular to the street. Write an equation representing the sidewalk. Step 1 Find the slope m of the street. y 2 – y 1 0 – 2 2 m = = = – 3 x 2 – x 1 3 – 0 3 6 -5 Points (0, 2) and (3, 0) are on the street.
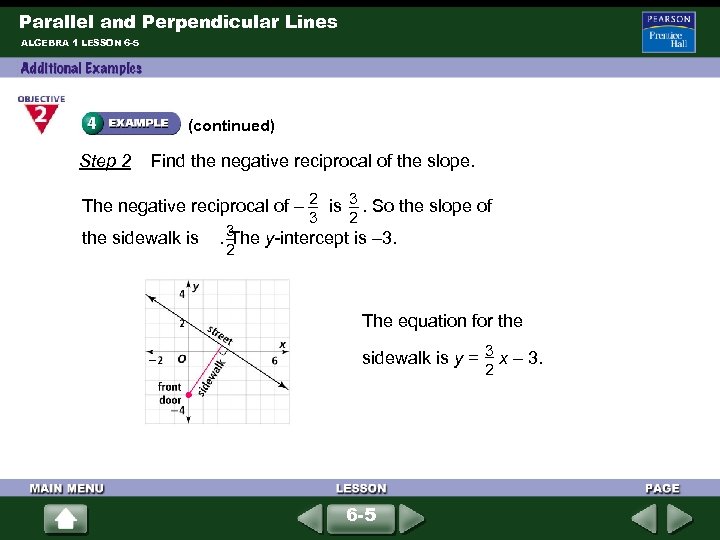
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 (continued) Step 2 Find the negative reciprocal of the slope. 2 3 The negative reciprocal of – is . So the slope of 3 2 3 the sidewalk is . The y-intercept is – 3. 2 The equation for the 3 sidewalk is y = x – 3. 2 6 -5
Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6 -5 1. Find the slope of a line parallel to 3 x – 2 y = 1. 3 2 2. Find the slope of a line perpendicular to 4 x + 5 y = 7. 5 4 Tell whether the lines for each pair of equations are parallel, perpendicular, or neither. 1 3 3. y = 3 x – 1, y = – x + 2 perpendicular 4. y = 2 x + 5, 2 x + y = – 4 neither 2 3 5. y = – x – 1, 2 x + 3 y = 6 parallel 6. Write an equation of the line that contains (2, 1) and is 1 2 perpendicular to y = – x + 3. 6 -5 y = 2 x – 3
Скачать презентацию Parallel and Perpendicular Lines ALGEBRA 1 LESSON 6
8bdc281fa599df3a87b45f9ca8e6a502.ppt