Pairwise sequence alignments Volker Flegel march 2003 Page

Pairwise sequence alignments Volker Flegel march 2003 Page 1

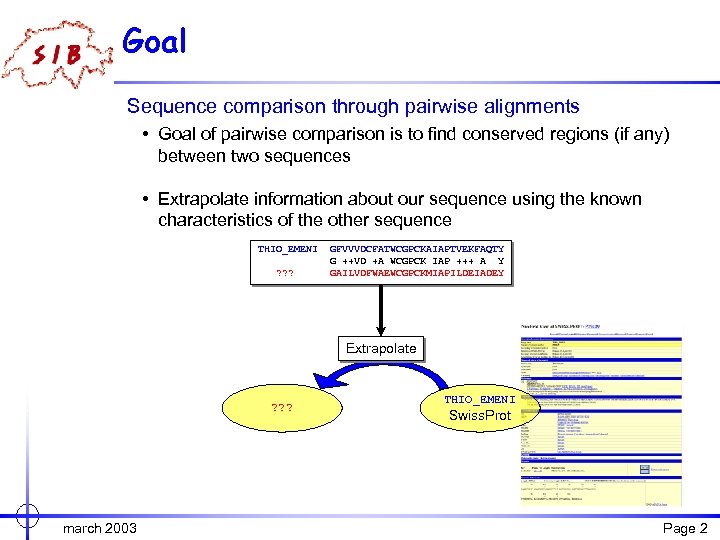Goal Sequence comparison through pairwise alignments • Goal of pairwise comparison is to find conserved regions (if any) between two sequences • Extrapolate information about our sequence using the known characteristics of the other sequence THIO_EMENI ? ? ? GFVVVDCFATWCGPCKAIAPTVEKFAQTY G ++VD +A WCGPCK IAP +++ A Y GAILVDFWAEWCGPCKMIAPILDEIADEY Extrapolate ? ? ? march 2003 THIO_EMENI Swiss. Prot Page 2

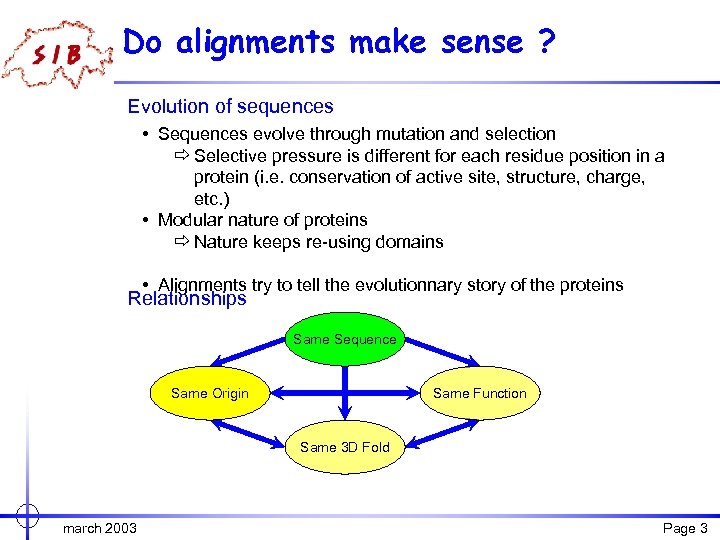Do alignments make sense ? Evolution of sequences • Sequences evolve through mutation and selection ð Selective pressure is different for each residue position in a protein (i. e. conservation of active site, structure, charge, etc. ) • Modular nature of proteins ð Nature keeps re-using domains • Alignments try to tell the evolutionnary story of the proteins Relationships Same Sequence Same Origin Same Function Same 3 D Fold march 2003 Page 3

Example: An alignment • Two similar regions of the Drosophila melanogaster Slit and Notch proteins 970 980 990 1000 1010 1020 SLIT_DROME FSCQCAPGYTGARCETNIDDCLGEIKCQNNATCIDGVESYKCECQPGFSGEFCDTKIQFC. . : : . : : : . : NOTC_DROME YKCECPRGFYDAHCLSDVDECASN-PCVNEGRCEDGINEFICHCPPGYTGKRCELDIDEC 740 750 760 770 780 790 march 2003 Page 4

Example: A diagonal plot • Comparing the tissue-type and urokinase type plasminogen activators Tissue-Type plasminogen Activator Urokinase-Type plasminogen Activator URL: www. isrec. isb-sib. ch/java/dotlet/Dotlet. html march 2003 Page 5

Relationships to other techniques Sequence analysis tools depending on pairwise comparison • Multiple alignments • Profile and HMM making (used to search for protein families and domains) • 3 D protein structure prediction • Phylogenetic analysis • Construction of certain substitution matrices • Similarity searches in a database march 2003 Page 6

Some definitions Identity Proportion of pairs of identical residues between two aligned sequences. Generally expressed as a percentage. This value strongly depends on how the two sequences are aligned. Similarity Proportion of pairs of similar residues between two aligned sequences. If two residues are similar is determined by a substitution matrix. This value also depends strongly on how the two sequences are aligned, as well as on the substitution matrix used. Homology Two sequences are homologous if and only if they have a common ancestor. There is no such thing as a level of homology ! (It's either yes or no) • Homologous sequences do not necessarily serve the same function. . . • not. march 2003. . . Nor are they always highly similar: structure may be conserved while sequence is Page 7

More definitions Consider a set S (say, globins) and a test t that tries to detect members of S (for example, through a pairwise comparison with another globin). True positive A protein is a true positive if it belongs to S and is detected by t. True negative A protein is a true negative if it does not belong to S and is not detected by t. False positive A protein is a false positive if it does not belong to S and is (incorrectly) detected by t. False negative A protein is a false negative if it belongs to S and is not detected by t (but should be). march 2003 Page 8

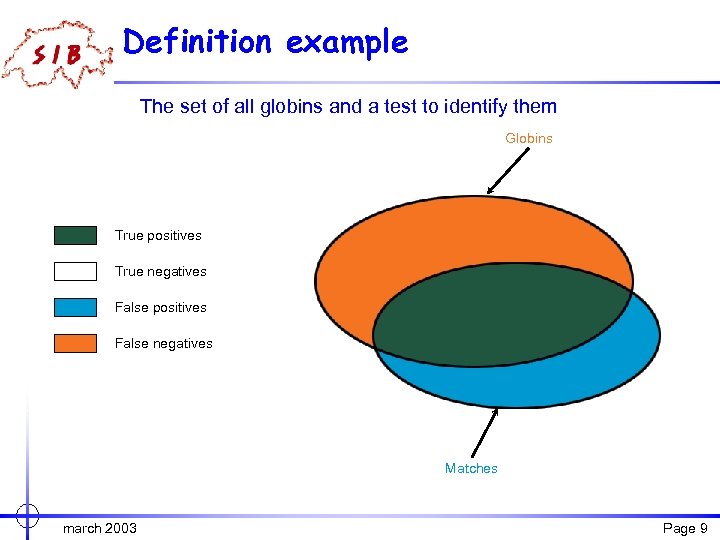Definition example The set of all globins and a test to identify them Globins True positives True negatives False positives False negatives Matches march 2003 Page 9

Even more definitions Sensitivity Ability of a method to detect positives, irrespective of how many false positives are reported. Selectivity Ability of a method to reject negatives, irrespective of how many false negatives are rejected. Greater sensitivity Less selectivity True positives True negatives False positives Less sensitivity Greater selectivity False negatives march 2003 Page 10

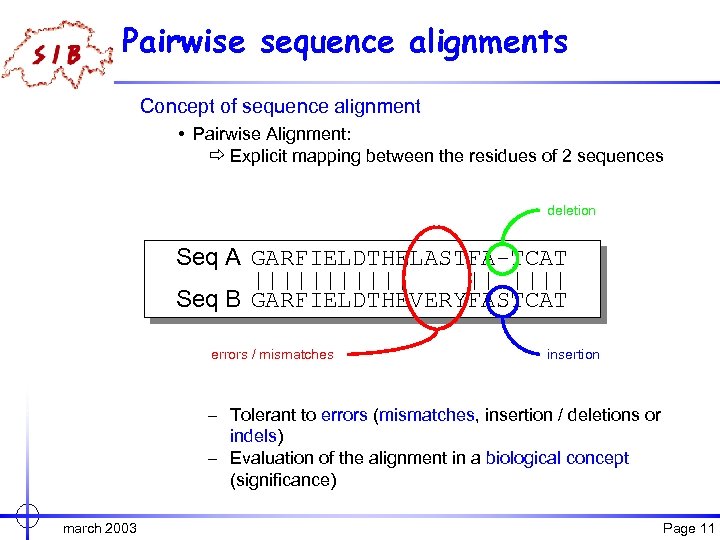Pairwise sequence alignments Concept of sequence alignment • Pairwise Alignment: ð Explicit mapping between the residues of 2 sequences deletion Seq A GARFIELDTHELASTFA-TCAT |||||| || |||| Seq B GARFIELDTHEVERYFASTCAT errors / mismatches insertion – Tolerant to errors (mismatches, insertion / deletions or indels) – Evaluation of the alignment in a biological concept (significance) march 2003 Page 11

Alignements Number of alignments • There are many ways to align two sequences • Consider the sequence fragments below: a simple alignment shows some conserved portions CGATGCAGACGTCA |||| CGATGCAAGACGTCA but also: CGATGCAGACGTCA |||| CGATGCAAGACGTCA • Number of possible alignments for 2 sequences of length 1000 residues: ð more than 10600 gapped alignments (Avogadro 1024, estimated number of atoms in the universe 1080) march 2003 Page 12

Alignement evaluation What is a good alignment ? • We need a way to evaluate the biological meaning of a given alignment • Intuitively we "know" that the following alignment: CGAGGCACAACGTCA ||| |||||| CGATGCAAGACGTCA is better than: ATTGGACAGCAATCAGG | || | | ACGATGCAAGACGTCAG • We can express this notion more rigorously, by using a scoring system. march 2003 Page 13

Scoring system Simple alignment scores • A simple way (but not the best) to score an alignment is to count 1 for each match and 0 for each mismatch. CGAGGCACAACGTCA ||| |||||| CGATGCAAGACGTCA ðScore: 12 ATTGGACAGCAATCAGG | || | | ACGATGCAAGACGTCAG ðScore: 5 march 2003 Page 14

Introducing biological information Importance of the scoring system ðdiscrimination of significant biological alignments • Based on physico-chemical properties of amino-acids ð Hydrophobicity, acid / base, sterical properties, . . . ð Scoring system scales are arbitrary • Based on biological sequence information ð Substitutions observed in structural or evolutionary alignments of well studied protein families ð Scoring systems have a probabilistic foundation Substitution matrices • In proteins some mismatches are more acceptable than others • Substitution matrices give a score for each substitution of one aminoacid by another march 2003 Page 15

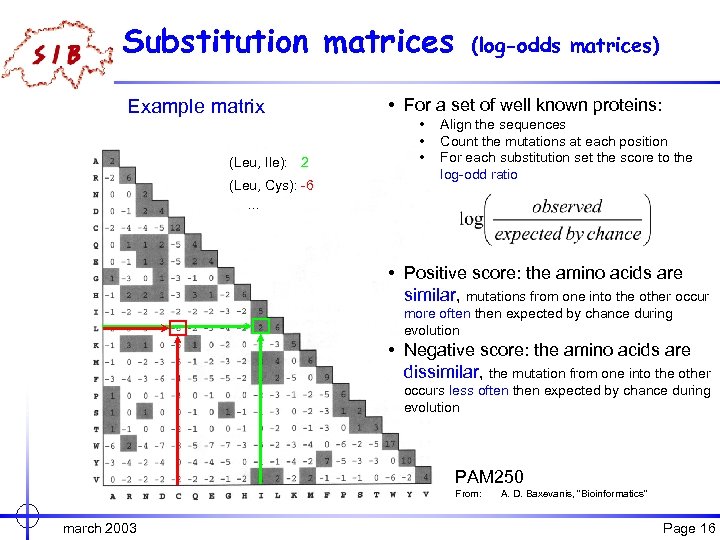Substitution matrices Example matrix (Leu, Ile): 2 (Leu, Cys): -6. . . (log-odds matrices) • For a set of well known proteins: • • • Align the sequences Count the mutations at each position For each substitution set the score to the log-odd ratio • Positive score: the amino acids are similar, mutations from one into the other occur more often then expected by chance during evolution • Negative score: the amino acids are dissimilar, the mutation from one into the other occurs less often then expected by chance during evolution PAM 250 From: march 2003 A. D. Baxevanis, "Bioinformatics" Page 16

Matrix choice Different kind of matrices • PAM series (M. Dayhoff, 1968, 1972, 1978) ð Based on 1572 protein sequences from 71 families ð Old standard matrix: PAM 250 • BLOSUM series ð Based on alignments in the BLOCKS database ð Standard matrix: BLOSUM 62 Limitations • Substitution matrices do not take into account long range interactions between residues. • They assume that identical residues are equal (a residue at the active site has other evolutionary constraints than the same residue outside of the active site) • They assume evolution rate to be constant. march 2003 Page 17

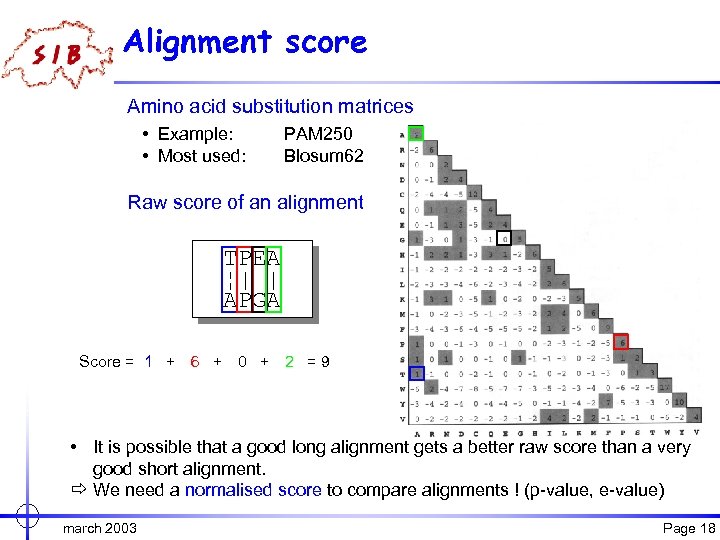Alignment score Amino acid substitution matrices • Example: • Most used: PAM 250 Blosum 62 Raw score of an alignment TPEA ¦| | APGA Score = 1 + 6 + 0 + 2 = 9 • It is possible that a good long alignment gets a better raw score than a very good short alignment. ð We need a normalised score to compare alignments ! (p-value, e-value) march 2003 Page 18

Gaps Insertions or deletions • Proteins often contain regions where residues have been inserted or deleted during evolution • There are constraints on where these insertions and deletions can happen (between structural or functional elements like: alpha helices, active site, etc. ) Gaps in alignments GCATGCAACTGCAT ||||| GCATGGGCAACTGCAT can be improved by inserting a gap GCATG--CAACTGCAT ||||||||| GCATGGGCAACTGCAT march 2003 Page 19

Gap opening and extension penalties Costs of gaps in alignments • We want to simulate as closely as possible the evolutionary mechanisms involved in gap occurence. Example • Two alignments with identical number of gaps but very different gap distribution. We may prefer one large gap to several small ones (e. g. poorly conserved loops between well-conserved helices) CGATGCAGCATCG ||||||| CGATGC------AGCATCG gap opening CGATGCAGCATCG || || || | CG-TG-AGCA-CA--AT-G gap extension Gap opening penalty • Counted each time a gap is opened in an alignment (some programs include the first extension into this penalty) Gap extension penalty • Counted for each extension of a gap in an alignment march 2003 Page 20

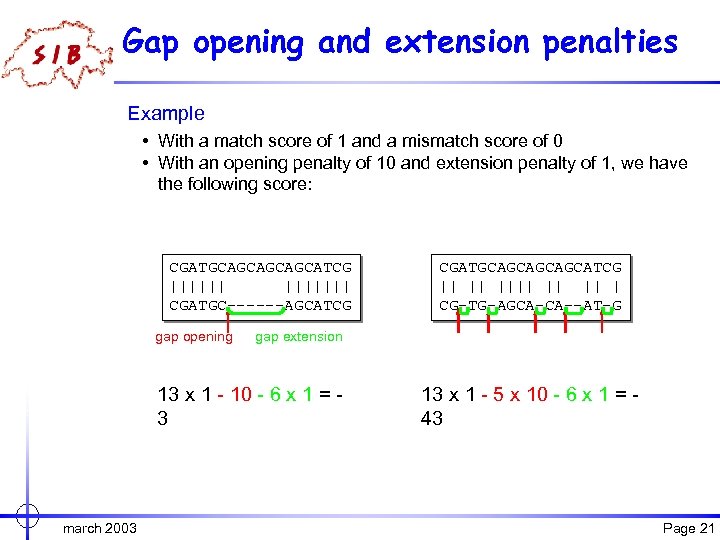Gap opening and extension penalties Example • With a match score of 1 and a mismatch score of 0 • With an opening penalty of 10 and extension penalty of 1, we have the following score: CGATGCAGCATCG ||||||| CGATGC------AGCATCG gap opening gap extension 13 x 1 - 10 - 6 x 1 = 3 march 2003 CGATGCAGCATCG || || || | CG-TG-AGCA-CA--AT-G 13 x 1 - 5 x 10 - 6 x 1 = 43 Page 21

Statistical evaluation of results Alignments are evaluated according to their score • Raw score ð It's the sum of the amino acid substitution scores and gap penalties (gap opening and gap extension) ð Depends on the scoring system (substitution matrix, etc. ) ð Different alignments should not be compared based only on the raw score • Normalised score ð Is independent of the scoring system ð Enables us to compare different alignments ð Units: expressed in bits march 2003 Page 22

Statistical evaluation of results Statistics derived from the scores • p-value ð Probability that an alignment with this score occurs by chance in a database of this size ð The closer the p-value is towards 0, the better the alignment • e-value ð Number of matches with this score one can expect to find by chance in a database of this size ð The closer the e-value is towards 0, the better the alignment march 2003 Page 23

Diagonal plots or Dotplot Concept of a Dotplot • Produces a graphical representation of similarity regions. • The horizontal and vertical dimensions correspond to the compared sequences. • A region of of similarity stands out as a diagonal. Tissue-Type plasminogen Activator Urokinase-Type plasminogen Activator march 2003 Page 24

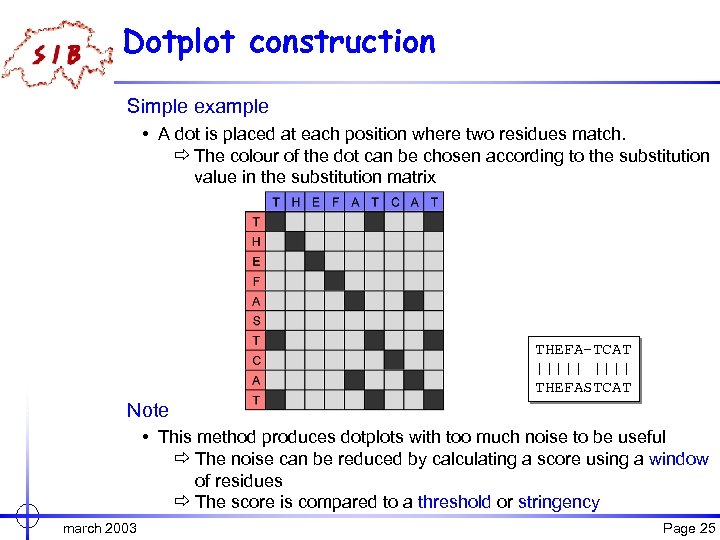Dotplot construction Simple example • A dot is placed at each position where two residues match. ð The colour of the dot can be chosen according to the substitution value in the substitution matrix THEFA-TCAT ||||| THEFASTCAT Note • This method produces dotplots with too much noise to be useful ð The noise can be reduced by calculating a score using a window of residues ð The score is compared to a threshold or stringency march 2003 Page 25

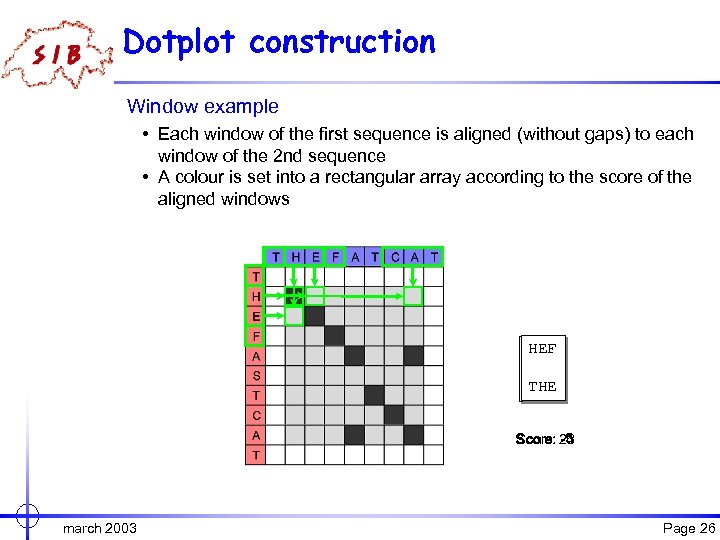Dotplot construction Window example • Each window of the first sequence is aligned (without gaps) to each window of the 2 nd sequence • A colour is set into a rectangular array according to the score of the aligned windows HEF THE CAT ||| THE HEF Score: 23 -5 -4 march 2003 Page 26

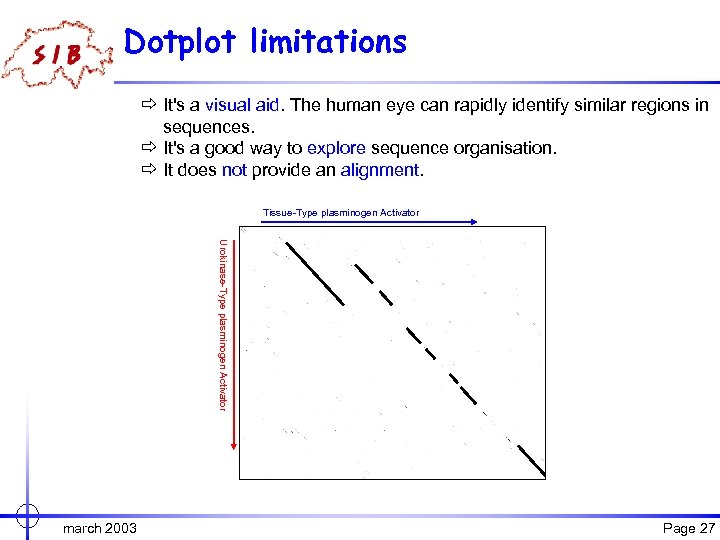Dotplot limitations ð It's a visual aid. The human eye can rapidly identify similar regions in sequences. ð It's a good way to explore sequence organisation. ð It does not provide an alignment. Tissue-Type plasminogen Activator Urokinase-Type plasminogen Activator march 2003 Page 27

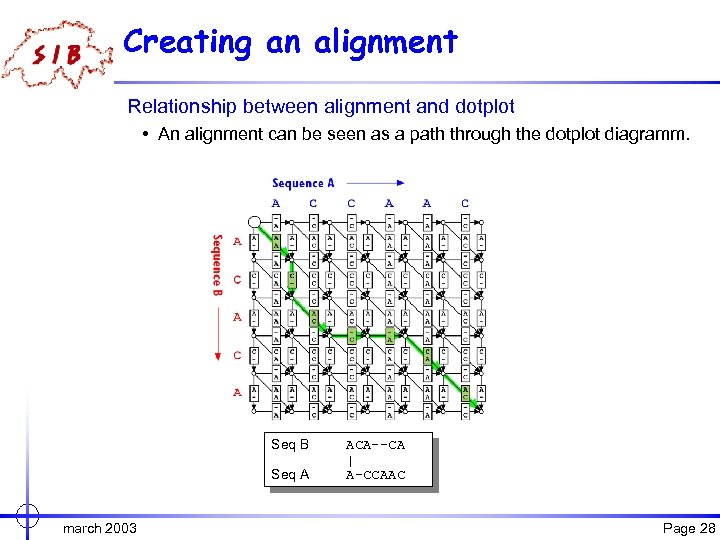Creating an alignment Relationship between alignment and dotplot • An alignment can be seen as a path through the dotplot diagramm. Seq B Seq A march 2003 ACA--CA A-CA-CA | || | A-CCAAC ACCAAC- Page 28

Finding an alignment Alignment algorithms • An alignment program tries to find the best alignment between two sequences given the scoring system. • This can be seen as trying to find a path through the dotplot diagram including all (or the most visible) diagonals. Alignement types • Global • Local Alignment between the complete sequence A and the complete sequence B Alignment between a sub-sequence of A an a subsequence of B Computer implementation (Algorithms) • Dynamic programing • Global Needleman-Wunsch • Local Smith-Waterman march 2003 Page 29

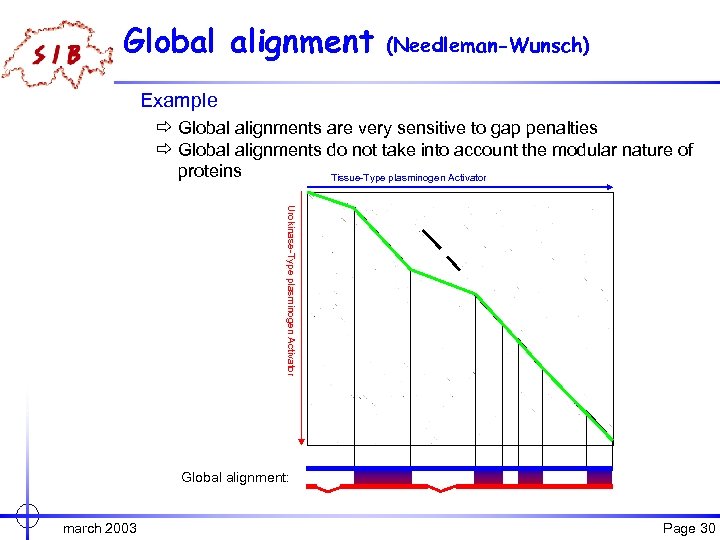Global alignment (Needleman-Wunsch) Example ð Global alignments are very sensitive to gap penalties ð Global alignments do not take into account the modular nature of proteins Tissue-Type plasminogen Activator Urokinase-Type plasminogen Activator Global alignment: march 2003 Page 30

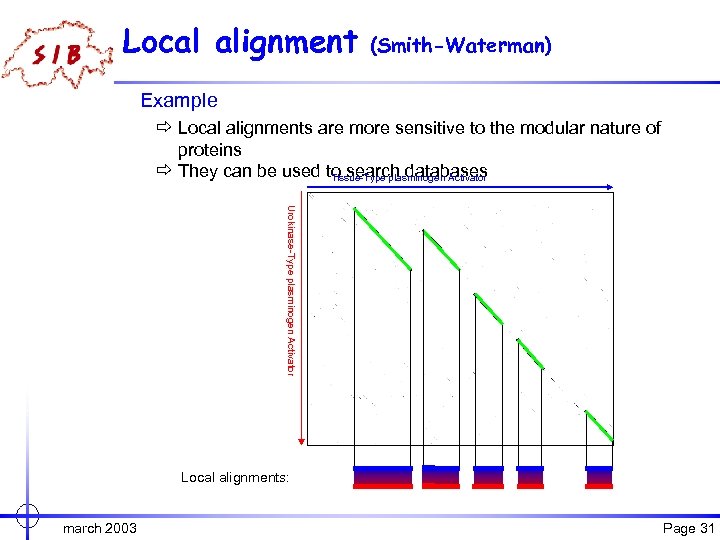Local alignment (Smith-Waterman) Example ð Local alignments are more sensitive to the modular nature of proteins ð They can be used to search databases Tissue-Type plasminogen Activator Urokinase-Type plasminogen Activator Local alignments: march 2003 Page 31

Optimal alignment extension How to extend optimaly an optimal alignment • An optimal alignment up to positions i and j can be extended in 3 ways. • Keeping the best of the 3 guarantees an extended optimal alignment. Seq A a a a. . . a a 1 Seq B Seq A 2 3 i-1 i b 1 b 2 b 3. . . bj-1 bj a 1 a 2 a 3. . . ai-1 ai ai+1 Seq B b 1 b 2 b 3. . . bj-1 bj bj+1 Seq A a 1 a 2 a 3. . . ai-1 ai Score = Scoreij + Substij ai+1 Seq B b 1 b 2 b 3. . . bj-1 bj - Seq A a 1 a 2 a 3. . . ai-1 ai Score = Scoreij - gap - Seq B march 2003 b 1 b 2 b 3. . . bj-1 bj bj+1 Score = Scoreij - gap • We have the optimal alignment extended from i and j by one residue. Page 32

Exact algorithms Simple example (Needleman-Wunsch) F(i-1, j- ð Match score: ð Mismatch score: ð Gap penalty: 2 -1 -2 F(i, j- 1) s(xi, yj) • Scoring system: 1) F(i- -d -d F(i, j) 1, j) F(i, j): score at position i, j s(xi, yj): match or mismatch score (or substitution matrix value) for residues xi and yj d: gap penalty (positive value) 0 -2 2+2 0 -2 Note GA-TTA || || GAATTC • We have to keep track of the origin of the score for each element in the matrix. ð This allows to build the alignment by traceback when the matrix has been completely filled out. • Computation time is proportional to the size of sequences (n x m). march 2003 Page 33

Algorithms for pairwise alignments Web resources • LALIGN - pairwise sequence alignment: www. ch. embnet. org/software/LALIGN_form. html • PRSS - alignment score evaluation: www. ch. embnet. org/software/PRSS_form. html Concluding remarks • Substitution matrices and gap penalties introduce biological information into the alignment algorithms. • It is not because two sequences can be aligned that they share a common biological history. The relevance of the alignment must be assessed with a statistical score. • There are many ways to align two sequences. Do not blindly trust your alignment to be the only truth. Especially gapped regions may be quite variable. • Sequences sharing less than 20% similarity are difficult to align: ð You enter the Twilight Zone (Doolittle, 1986) ð Alignments may appear plausible to the eye but are no longer statistically significant. ð Other methods are needed to explore these sequences (i. e: profiles) march 2003 Page 34