Packing directed cycles efficiently Zeev Nutov Raphael Yuster

Packing directed cycles efficiently Zeev Nutov Raphael Yuster 1

Definitions and notations • Given a digraph G, how many arcdisjoint cycles can be packed into G? This value is the cycle packing number νc(G) of G. • νc*(G) = max fractional cycle packing. • Clearly νc*(G) ≤ νc(G). • Computing νc(G) is NP-Hard. Computing νc*(G) is in P (using LP). • How far apart can they be? 2

Main result and its algorithmic consequences Theorem: νc*(G) - νc(G) = o(n 2). Furthermore, a set of νc(G) - o(n 2) arc -disjoint cycles can be found in randomized polynomial time. Corollary: νc(G) can be approximated to within an o(n 2) additive term in polynomial time. This implies a FPTAS for computing νc(G) for almost all digraphs, since νc(G) = θ(n 2) for almost all digraphs. 3

A more general result • Let F be any fixed (finite or infinite) family of oriented graphs. ν(F, G) = max F–packing value in G. ν*(F, G) = max fractional F–packing. Theorem: ν*(F, G) - ν(F, G) =o(n 2). • Our result for cycles follows by letting F be the family of all cycles and from the fact that all 2 -cycles appear in any max cycle packing. • The special case where F is a single undirected graph has been proved by Haxell and Rödl (Combinatorica 2001) 4

Tools used - 1 Directed version of Szemeredi’s regularity lemma: (Alon and Shapira, STOC 2003). – A bipartite digraph with vertex classes A , B is called γ-regular if |d(A, B) – d(X, Y)|<γ |d(B, A) – d(Y, X)|<γ for all X A, |X| > γ|A|, Y B, |Y| > γ|B|, where d(. , . ) is the arc density of the pair. – A γ-regular partition of V is an equitable partition such that all (but a γ-fraction) of the part pairs are γ-regular. – For every γ>0, there is an integer M(γ)>0 such that every digraph G of order n > M has a γ-regular partition of its vertex set into m parts, for some 1/γ < m < M. 5

Tools used - 2 A “random-like behavior lemma”: For reals δ , ζ and positive integer k there exist γ = γ(δ, ζ, k) and T=T(δ, ζ, k) such that: Any k-partite oriented graph H with parts V 1, …, Vk with |Vi|=t >T that satisfies: - each pair (Vi, Vi+1) is γ-regular; - d(Vi, Vi+1) > δ, has a spanning subgraph H' with at least -ζ)|E(H)| arcs such that for e E(Vi, Vi+1) (1 |c(e)/tk-2 - ∏d(j, j+1)| < ζ j≠i where c(e) = number of Ck in H' containing e. 6

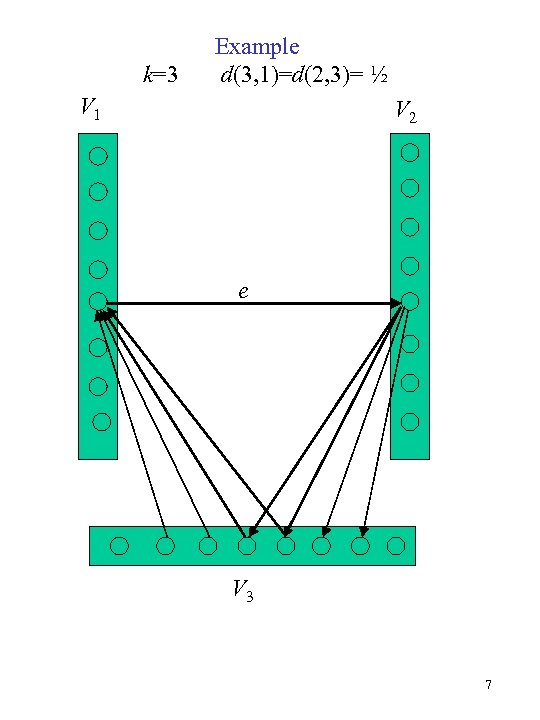k=3 Example d(3, 1)=d(2, 3)= ½ V 1 V 2 e V 3 7

Tools used – 3 Frankl-Rödl hypergraph matching theorem: For an integer r > 1 and a real β > 0 there exists a real μ > 0 so that if an r-uniform hypergraph on q vertices has the following properties for some d: (i) (1 - μ)d < deg(x) < (1+ μ)d for all x (ii) deg(x, y) < μd for all distinct x and y then there is a matching of size at least (q/r)(1 -β). 8

Tools used – 4 Theorem: A maximum fractional dicycle packing of G yielding νc*(G) can be computed in polynomial time. Remark: Computing νc*(G) is in P via solving the dual LP. But finding an appropriate weight function w on the cycle set of G is not straightforward (there is always an optimal fractional packing in which only O(n 2) cycles receive nonzero weight). 9

The proof • Let ε > 0. We shall prove: There exists N=N(ε) such that for all n > N, if G is an n-vertex oriented graph then ν*c(G) - νc(G) < εn 2. • A consistent “horrible” parameter selection: – k 0=20/ε (“long” cycles are ignored) – δ=β=ε/4. – μ=μ(β, k 0) of Frankl-Rödl. – ζ= 0. 5μδk. – γ=γ(δ, ζ , k 0) T=T(δ, ζ , k 0) as in the “random-like behavior lemma”. – M=M(γε/25 k 0) as in regularity lemma. – N = suff. large w. r. t. these parameters. 0 • Fix an n-vertex oriented graph G with n > N. Let ψ be a fractional dicycle packing with w(ψ)= ν*c(G) = αn 2 > εn 2. 10

The proof cont. • Apply directed regularity lemma to G and obtain a γ' -regular partition with m' parts, where γ' =γε/(25 k 0) and 1/γ' < m' < M(γ'). • Refine the partition by randomly partitioning each part into 25 k 0/ε parts. The refined partition is now γ-regular. What we gain: with positive probability the contribution of bad cycles (cycles with two vertices in the same vertex class) to w(ψ) is less than εn 2/20. We may therefore assume that there are no bad cycles. • Let V 1, …, Vm be the vertex classes of the refined partition, m = m' (25 k 0/ε). 11

The proof cont. • Let G* be the spanning subgraph of G consisting of the arcs connecting part pairs that are γ-regular and with density > δ. • Let ψ* be the restriction of ψ to G* (namely, “surviving” cycles). It is easy to show that ν*c(G*) ≥ w(ψ*) > w(ψ)- δn 2 = (α-δ)n 2. • Let G be the m-vertex super-digraph obtained from G* by contracting each part. Define a fractional packing ψ' of G by “gluing” parallel cycles and scaling by m 2 / n 2. • Observation: ψ' is proper and ν*c(G ) ≥ w(ψ') = w(ψ*) m 2/n 2 ≥ (α-δ)m 2. 12

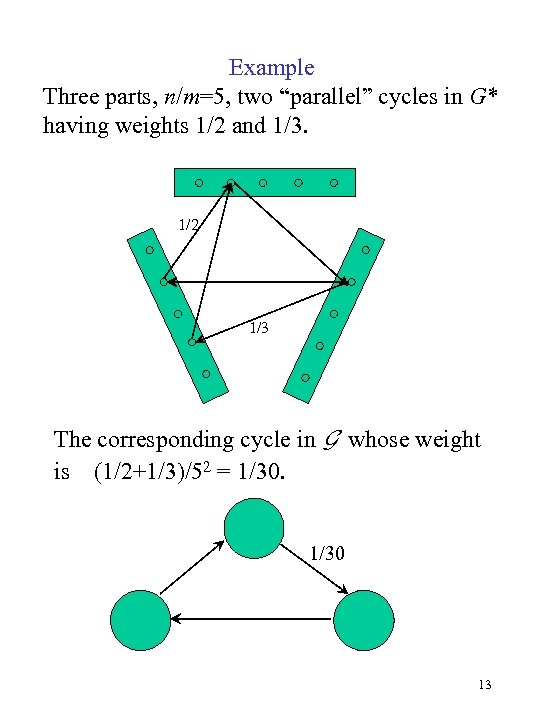Example Three parts, n/m=5, two “parallel” cycles in G* having weights 1/2 and 1/3. 1/2 1/3 The corresponding cycle in G whose weight is (1/2+1/3)/52 = 1/30 13

The proof cont. Use ψ' to define a random coloring of the arcs of G*. The “colors” are the cycles of G. Let e E(Vi, Vj) be an arc of G*. For each cycle C in G that contains the arc (i, j), e is colored “C” with probability ψ'(C)/d(i, j). – The choices made for distinct arcs of G* are independent. – The random coloring is probabilistically sound as ψ' is a proper fractional packing. Thus S{ψ'(C): (i, j) C} ≤ d(i, j) ≤ 1. – Some arcs might stay uncolored. 14

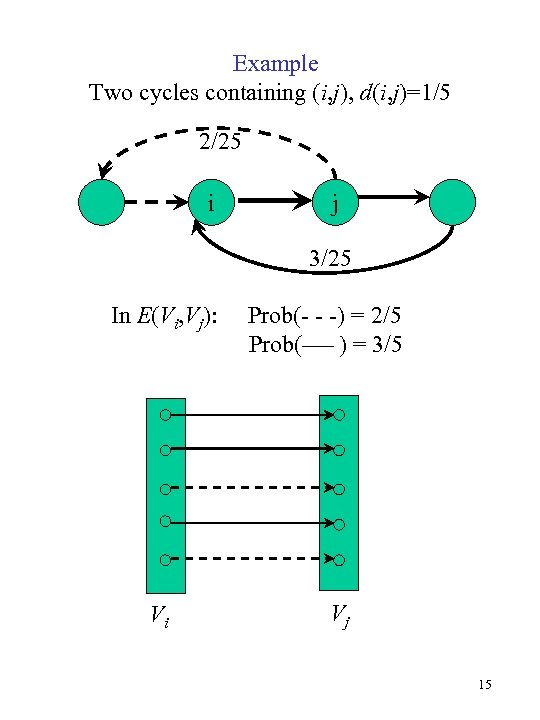Example Two cycles containing (i, j), d(i, j)=1/5 2/25 i j 3/25 In E(Vi, Vj): Vi Prob(- - -) = 2/5 Prob(___ ) = 3/5 Vj 15

The proof cont. • Let C ={1, …, k} in G with ψ'(C) > m 1 -k. Let GC = G*[V 1, …, Vk]. – GC satisfies the conditions of the randomlike behavior lemma. – Let G'C be the spanning subgraph of GC with properties guaranteed by the lemma. – Let JC denote the random spanning subgraph of GC consisting only of the arcs whose “color” is C. – For an arc e E(JC), let c. C(e) be the number of Ck copies in JC containing e. Lemma: Let e E(JC). With probability > 1 -m 3/n | c. C(e)/tk-2 - ψ'(C)k-1 | < μ ψ'(C)k-1. 16

The proof cont. • We also need a lower bound for the number of arcs of JC : With probability at least 1 -1/n, |E(JC)| > k(1 -2ζ) ψ'(C) n 2/m 2. • Since there at most O(mk 0) cycles in G we have that with probability at least 1 -O(mk 0/n) – O(mk 0+3/n) > 0 all cycles C in G with ψ'(C) > m 1 -k 0 satisfy the statements of the last two lemmas. We therefore fix such a coloring. 17

The proof cont. • Let C be a k-cycle in G with ψ'(C) > m 1 -k 0. We construct a k-uniform hypergraph HC: – The vertices of HC are the arcs of JC. – The edges of HC are the arc sets of the copies of Ck in JC. • Our hypergraph satisfies the FR theorem with d=tk-2 ψ'(C)k-1. • By FR: (q/k)(1 -β) arc disjoint Ck in JC. As q > k(1 -2ζ) ψ'(C) n 2 / m 2 we have (1 -β) (1 -2ζ) ψ'(C) n 2 /m 2 ≥ (1 -2β)ψ'(C)n 2 /m 2. • Recall that w(ψ') ≥ m 2(α-δ). Since the contribution of copies with ψ'(C) ≤ m 1 -k 0 to w(ψ') is < m, summing the last inequality over all cycles C with ψ'(C) > m 1 -k 0 we have at least (α-ε)n 2 arc disjoint cycles in G. 18