П О В Т О Р Е Н И Е. Линейная функция.
Линейной функцией называется функция вида у = kx + b где k и b – заданные числа у = kx + b Графиком линейной функции является прямая k- угловой коэффициент (k =tgα) b – ордината точки пересечения с осью y
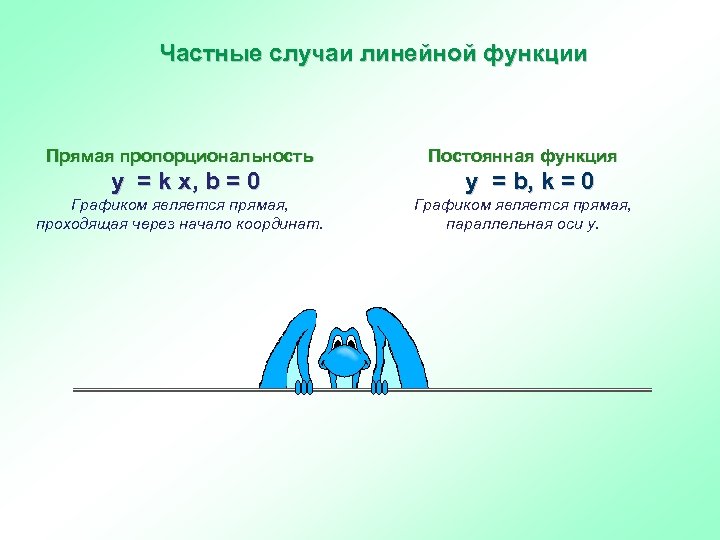Частные случаи линейной функции Прямая пропорциональность y = k x, b = 0 Графиком является прямая, проходящая через начало координат. Постоянная функция y = b, k = 0 Графиком является прямая, параллельная оси у.
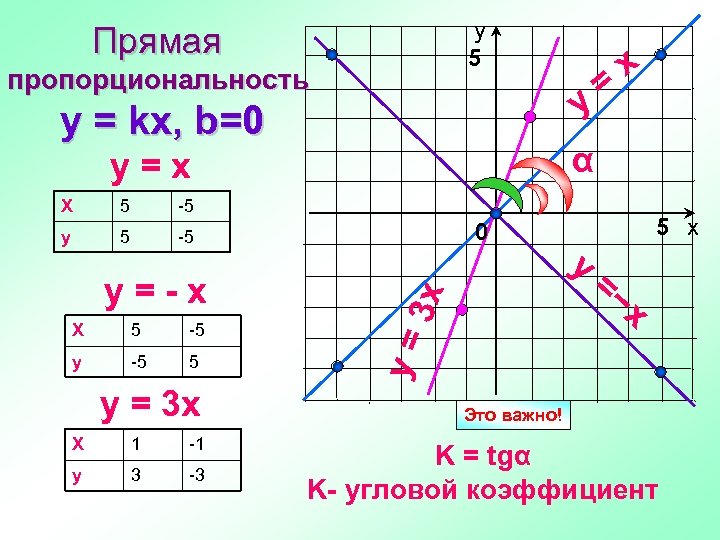у 5 Прямая пропорциональность y y = kx, b=0 α y=x -5 y 5 -5 y=-x X 5 -5 y -5 5 y = 3 x X 1 -1 y 3 -3 0 y 5 х =− x 3 x 5 y= X = x Это важно! K = tgα K- угловой коэффициент
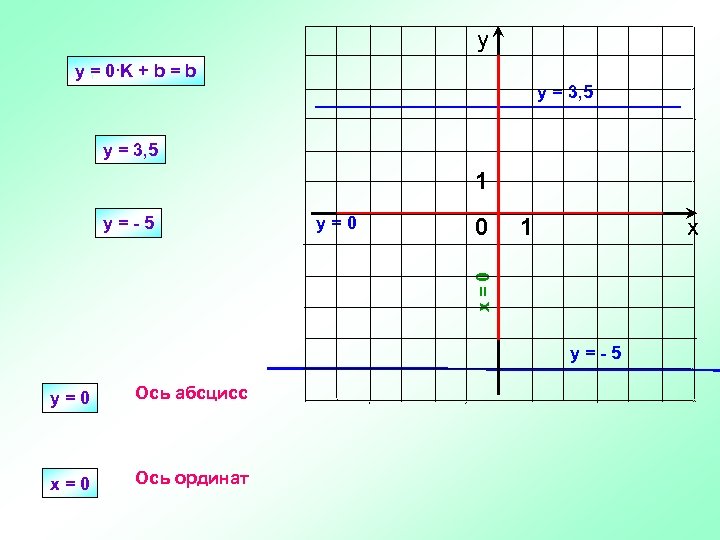у y = 0∙K + b = b y = 3, 5 1 y=0 0 1 х x=0 y=-5 у=0 Ось абсцисс х=0 Ось ординат
Взаимное расположение графиков линейной функции
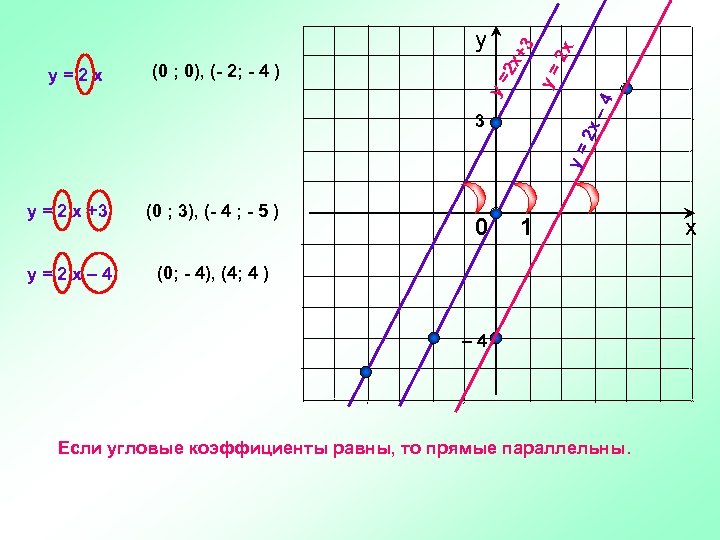2 x +3 – 4 y= (0 ; 0), (- 2; - 4 ) y= y=2 x 2 x у y= 2 x 3 y = 2 x +3 (0 ; 3), (- 4 ; - 5 ) y=2 x– 4 (0; - 4), (4; 4 ) 0 1 – 4 Если угловые коэффициенты равны, то прямые параллельны. х
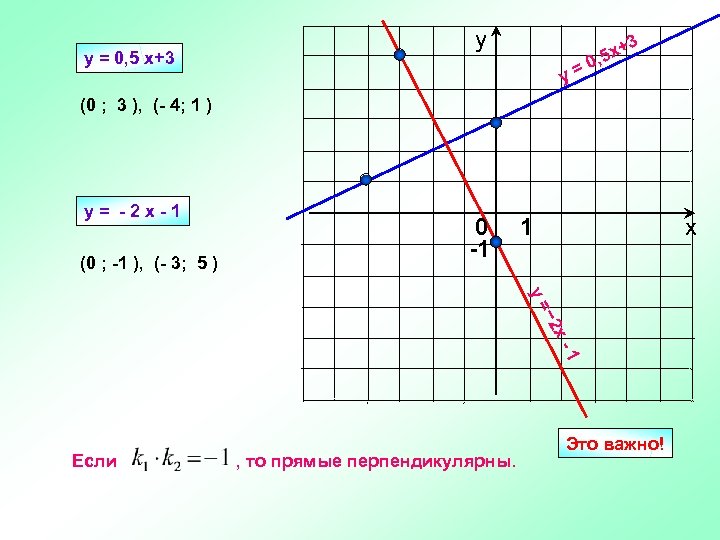y = 0, 5 x+3 у 3 y= + , 5 x 0 (0 ; 3 ), (- 4; 1 ) y= -2 х-1 (0 ; -1 ), (- 3; 5 ) 0 -1 1 х − 2 y= х1 Если , то прямые перпендикулярны. Это важно!
Свойства линейной функции у = kx + b при k ≠ 0, b ≠ 0 Ø Область определения функции – множество всех действительных чисел. D(f) = (-∞ ; + ∞) Ø Множество значений функции – множество всех действительных чисел. Е(f) = (-∞ ; + ∞) Ø Функция не является ни четной, ни нечетной Ø Нули функции: y = 0 при х = - b / k Ø Промежутки знакопостоянства. если k > 0, то y > 0 на (- b / k ; + ∞); если k < 0, то y > 0 на ( -∞; - b / k ); y < 0 на ( -∞; - b / k ) y < 0 на (- b / k ; + ∞) Ø Промежутки монотонности. если k > 0, то функция возрастает на (- ∞; + ∞); если k < 0, то функция убывает на (- ∞; + ∞)
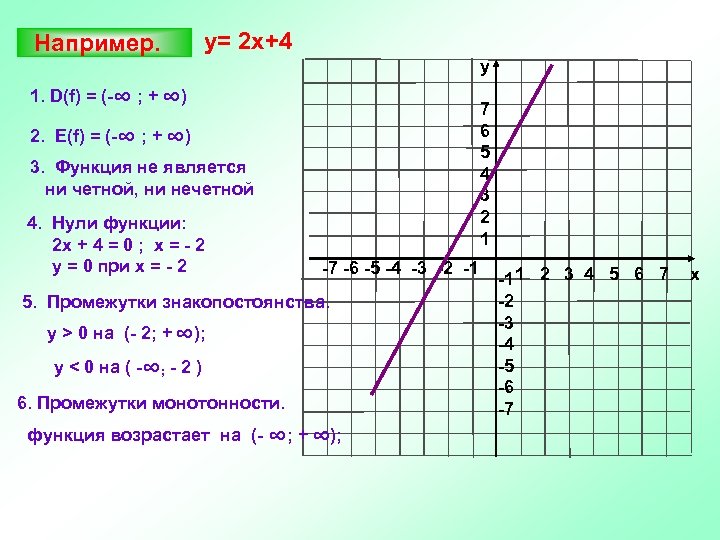Например. у= 2 х+4 y 1. D(f) = (-∞ ; + ∞) 7 6 5 4 3 2 1 2. Е(f) = (-∞ ; + ∞) 3. Функция не является ни четной, ни нечетной 4. Нули функции: 2 х + 4 = 0 ; х = - 2 у = 0 при х = - 2 -7 -6 -5 -4 -3 -2 -1 5. Промежутки знакопостоянства. y > 0 на (- 2; + ∞); y < 0 на ( -∞; - 2 ) 6. Промежутки монотонности. функция возрастает на (- ∞; + ∞); -1 1 2 3 4 5 6 7 -2 -3 -4 -5 -6 -7 x
Свойства линейной функции у = kx при k ≠ 0, b = 0 Ø Область определения функции – множество всех действительных чисел. D(f) = (-∞ ; + ∞) Ø Множество значений функции – множество всех действительных чисел. Е(f) = (-∞ ; + ∞) Ø Функция нечетная Ø Нули функции: y = 0 при х = 0 Ø Промежутки знакопостоянства. если k > 0, то y > 0 на (0 ; + ∞); если k < 0, то y > 0 на ( -∞; 0) ; y < 0 на ( -∞; 0 ) y < 0 на (0 ; + ∞) Ø Промежутки монотонности. если k > 0, то функция возрастает на (- ∞; + ∞); если k < 0, то функция убывает на (- ∞; + ∞)
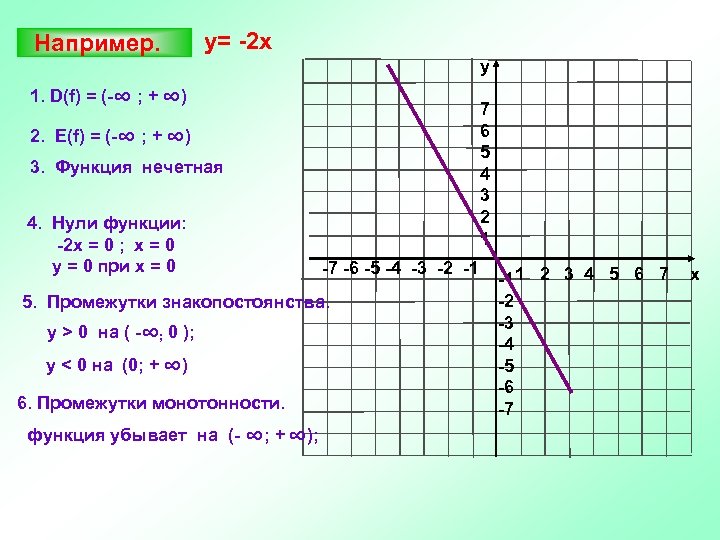Например. у= -2 х y 1. D(f) = (-∞ ; + ∞) 7 6 5 4 3 2 1 2. Е(f) = (-∞ ; + ∞) 3. Функция нечетная 4. Нули функции: -2 х = 0 ; х = 0 у = 0 при х = 0 -7 -6 -5 -4 -3 -2 -1 5. Промежутки знакопостоянства. y > 0 на ( -∞; 0 ); y < 0 на (0; + ∞) 6. Промежутки монотонности. функция убывает на (- ∞; + ∞); -1 1 2 3 4 5 6 7 -2 -3 -4 -5 -6 -7 x
Свойства линейной функции у = b при k = 0, b ≠ 0 Ø Область определения функции – множество всех действительных чисел. D(f) = (-∞ ; + ∞) Ø Множество значений функции состоит из одного числа b. Е(f) = {b} Ø Функция четная Ø Нули функции: нулей нет Ø Промежутки знакопостоянства. если b > 0, то y > 0 на ( -∞; + ∞) если b < 0, то y < 0 на ( -∞; + ∞) Ø Промежутки монотонности. Функция постоянна
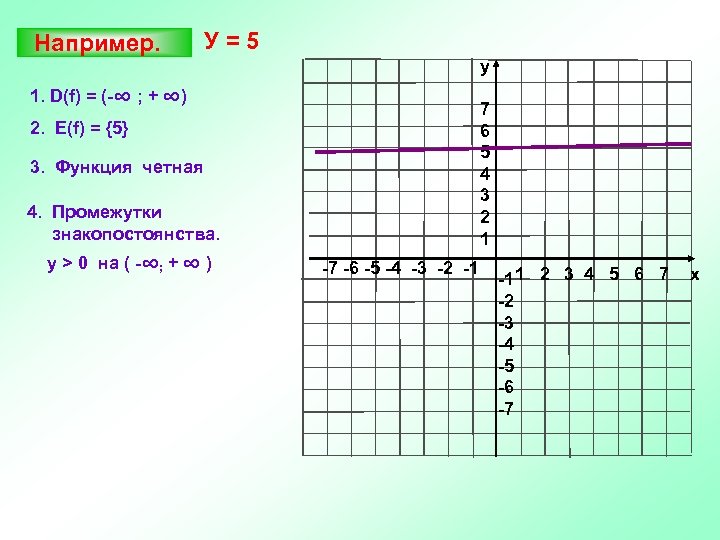Например. У=5 y 1. D(f) = (-∞ ; + ∞) 7 6 5 4 3 2 1 2. Е(f) = {5} 3. Функция четная 4. Промежутки знакопостоянства. y > 0 на ( -∞; + ∞ ) -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 -2 -3 -4 -5 -6 -7 x
Литература и интернет- ресурсы: • Сайт учителя математики Савченко Елены Михайловны http: //le-savchen. ucoz. ru/load/14 -1 -0 -188 • Генденштейн Л. Э. и др. Наглядный справочник по математике с примерами. Для абитуриентов, школьников, учителей. – М. : Илекса, 2005 • Гусев В. А. , Мордкович А. Г. Справочные материалы по математике для подготовки к экзаменам. - М. : ООО «Издательство АСТ» : ООО «Издательство Астрель» , 2004.