Скачать презентацию P Grannis LPNHE Univ Paris VI
c7d48a97fccb53a15d836de32a6daf5f.ppt
- Количество слайдов: 35
P. Grannis / LPNHE Univ. Paris VI & VII Dec 13, 2001 Physics at the e+e. Linear Collider The Linear Collider will be a demanding and expensive project – it had better address the big questions confronting particle physics : v. What is the origin of Electroweak symmetry breaking? What gives mass to all particles? What is the new physics at the Te. V scale? (believe there is something!) What protects the Higgs/W/Z masses (hierarchy problem) v Where do the quark and lepton flavors come from ? Why 3 generations of quarks and leptons? Why CP violation and why the baryon/antibaryon asymmetry in universe? Why fermion mass disparities & mixing patterns (all those arbitrary parameters)? v What are the unseen elements of the universe ? What is the dark matter & dark energy? Why is the cosmological constant so small ( 0) and the universe flat ?
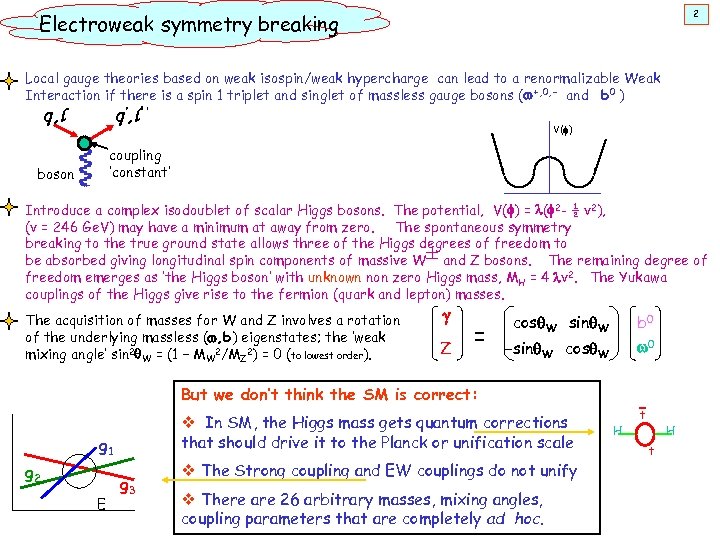2 Electroweak symmetry breaking Local gauge theories based on weak isospin/weak hypercharge can lead to a renormalizable Weak Interaction if there is a spin 1 triplet and singlet of massless gauge bosons (w+, 0, - and b 0 ) q, l q’, l’ ‘ V(f) coupling ‘constant’ boson Introduce a complex isodoublet of scalar Higgs bosons. The potential, V(f) = l(f 2 - ½ v 2), (v = 246 Ge. V) may have a minimum at away from zero. The spontaneous symmetry breaking to the true ground state allows three of the Higgs degrees of freedom to be absorbed giving longitudinal spin components of massive W and Z bosons. The remaining degree of freedom emerges as ‘the Higgs boson’ with unknown non zero Higgs mass, MH = 4 lv 2. The Yukawa couplings of the Higgs give rise to the fermion (quark and lepton) masses. The acquisition of masses for W and Z involves a rotation of the underlying massless (w, b) eigenstates; the ‘weak mixing angle’ sin 2 q. W = (1 – MW 2/MZ 2) = 0 (to lowest order). g Z = cosq. W sinq. W b 0 -sinq. W cosq. W w 0 But we don’t think the SM is correct: v In SM, the Higgs mass gets quantum corrections that should drive it to the Planck or unification scale g 1 g 2 E g 3 v The Strong coupling and EW couplings do not unify v There are 26 arbitrary masses, mixing angles, coupling parameters that are completely ad hoc. H t
Supersymmetry 3 Supersymmetry offers a popular way to solve the hierarchy problem; if there are neardegenerate pairs of fermions and bosons with otherwise identical properties and couplings, the loop divergences due to fermions and bosons cancel, curing the hierarchy problem. For example, the partner of the left-handed e- with spin ½ would be a selectron ~ e. L- with spin 0. Since we don’t observe such a state with m = 0. 511 Me. V, we know that supersymmetry must be broken. If there is supersymmetry, there is a new space-time of ‘fermionic’ dimensions. Supersymmetry occurs in string theories (at the Planck scale). To make supersymmetry work, need two complex Higgs doublets f 1 and f 2 to give mass separately to up- and down-type fermions. After EWSB giving W/Z masses, 5 Higgs states survive: h 0, H 0 (scalars), A 0 (pseudoscalar) and H (charged Higgs). The ratio
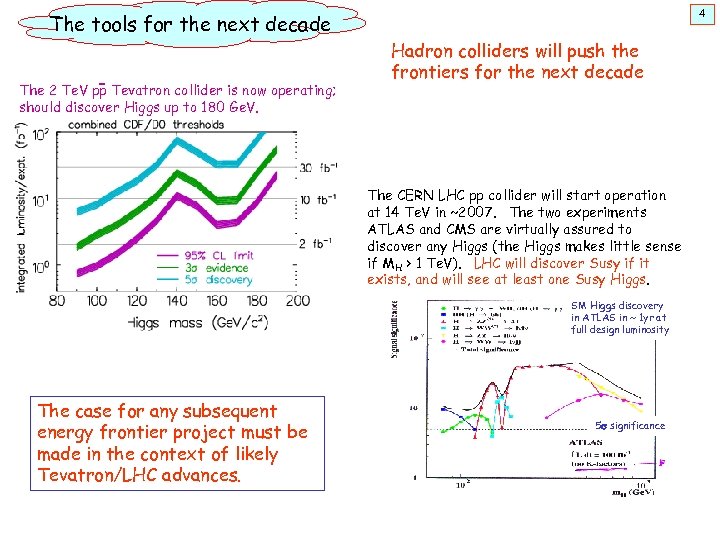4 The tools for the next decade The 2 Te. V pp Tevatron collider is now operating; should discover Higgs up to 180 Ge. V. Hadron colliders will push the frontiers for the next decade The CERN LHC pp collider will start operation at 14 Te. V in ~2007. The two experiments ATLAS and CMS are virtually assured to discover any Higgs (the Higgs makes little sense if MH > 1 Te. V). LHC will discover Susy if it exists, and will see at least one Susy Higgs. SM Higgs discovery in ATLAS in ~ 1 yr at full design luminosity The case for any subsequent energy frontier project must be made in the context of likely Tevatron/LHC advances. 5 s significance
5 Lepton colliders Although Tevatron/LHC should make the discoveries, they will not be able to measure the crucial properties of Higgs that tell us what it really is, and cannot make critical Susy measurements to pin down the model or explain Supersymmetry breaking. Lepton-lepton colliders offer complementary strengths to hadron colliders, and in the past, both have been necessary to fully understand particle properties. e+e- colliders produce final state fermion pairs (leptons or quarks) or boson pairs (ZH) via s-channel g or Z exchange (or WW fusion). e+ e- g, Z f f The strengths of the lepton colliders arise from the well defined initial parton energy and quantum numbers (JP = 1 -). The final states of interest are relatively free of backgrounds due to the absence of strong interactions for the leptons. The drawbacks are the fixed partonic CM energy, and the lower ECM than for hadron machines. Much work over the past 10 years on high intensity Linear e +e- Colliders. The electron beams (perhaps positrons) may be polarized, giving more incisive control of reactions. It is possible to Compton backscatter laser light from the e beam giving nearly monochromatic high energy g’s that can be used for eg or gg collisions – useful for special studies. Recently proposals have been made for muon colliders, using very high intensity proton beams creating p → mn; m capture; m cooling (reduction of phase space) and m acceleration. Much R&D remains, and muon colliders are probably 15 years away (but an adaptation may make a muon storage ring as an intense source of n somewhat sooner).
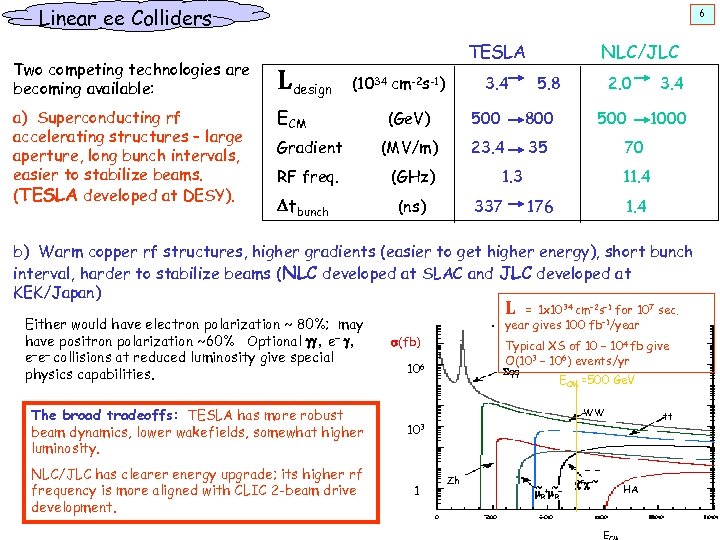Linear ee Colliders 6 Two competing technologies are becoming available: Ldesign a) Superconducting rf accelerating structures – large aperture, long bunch intervals, easier to stabilize beams. (TESLA developed at DESY). TESLA ECM (1034 cm-2 s-1) 3. 4 NLC/JLC 5. 8 (Ge. V) 500 800 Gradient (MV/m) 23. 4 35 RF freq. (GHz) Dtbunch (ns) 2. 0 500 1000 70 1. 3 337 3. 4 11. 4 176 1. 4 b) Warm copper rf structures, higher gradients (easier to get higher energy), short bunch interval, harder to stabilize beams (NLC developed at SLAC and JLC developed at KEK/Japan) Either would have electron polarization ~ 80%; may have positron polarization ~60% Optional gg, e-e- collisions at reduced luminosity give special physics capabilities. L = 1 x 1034 cm-2 s-1 for 107 sec. year gives 100 fb-1/year s(fb) Typical XS of 10 – 104 fb give O(103 – 106) events/yr 106 The broad tradeoffs: TESLA has more robust beam dynamics, lower wakefields, somewhat higher luminosity. 1 ECM =500 Ge. V 103 NLC/JLC has clearer energy upgrade; its higher rf frequency is more aligned with CLIC 2 -beam drive development. Sqq WW Zh ~ +m m ~ R ~ ~ c +c - tt HA R E
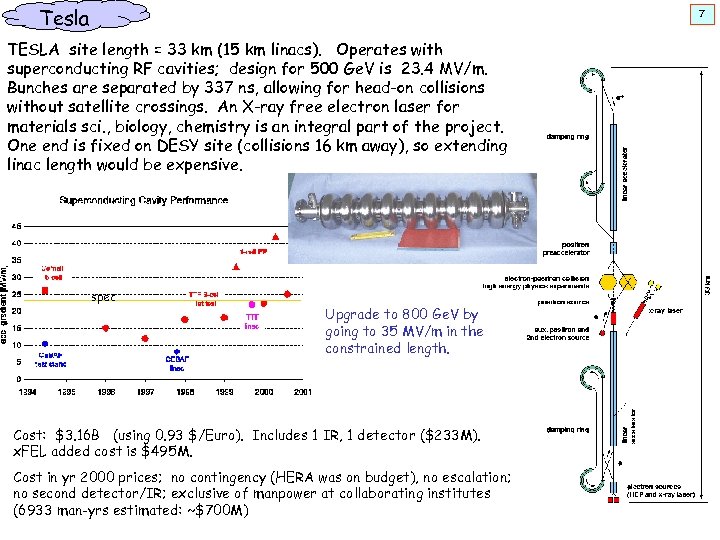Tesla 7 TESLA site length = 33 km (15 km linacs). Operates with superconducting RF cavities; design for 500 Ge. V is 23. 4 MV/m. Bunches are separated by 337 ns, allowing for head-on collisions without satellite crossings. An X-ray free electron laser for materials sci. , biology, chemistry is an integral part of the project. One end is fixed on DESY site (collisions 16 km away), so extending linac length would be expensive. spec Upgrade to 800 Ge. V by going to 35 MV/m in the constrained length. Cost: $3. 16 B (using 0. 93 $/Euro). Includes 1 IR, 1 detector ($233 M). x. FEL added cost is $495 M. Cost in yr 2000 prices; no contingency (HERA was on budget), no escalation; no second detector/IR; exclusive of manpower at collaborating institutes (6933 man-yrs estimated: ~$700 M)
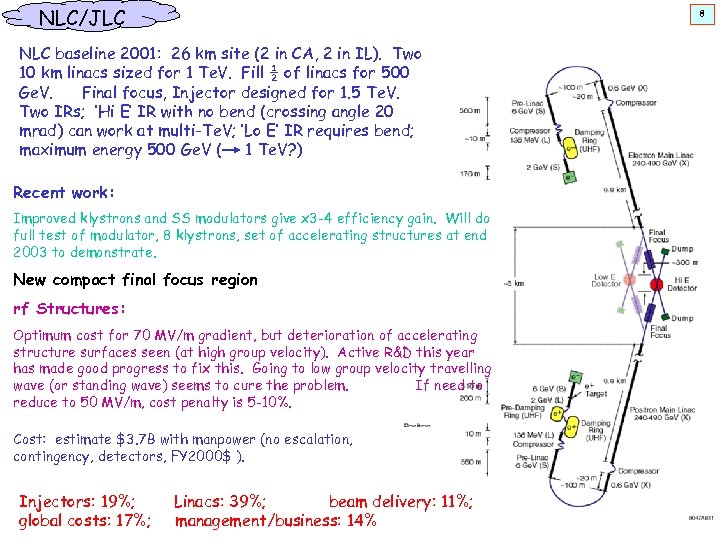NLC/JLC 8 NLC baseline 2001: 26 km site (2 in CA, 2 in IL). Two 10 km linacs sized for 1 Te. V. Fill ½ of linacs for 500 Ge. V. Final focus, Injector designed for 1. 5 Te. V. Two IRs; ‘Hi E’ IR with no bend (crossing angle 20 mrad) can work at multi-Te. V; ‘Lo E’ IR requires bend; maximum energy 500 Ge. V ( 1 Te. V? ) Recent work: Improved klystrons and SS modulators give x 3 -4 efficiency gain. Will do full test of modulator, 8 klystrons, set of accelerating structures at end 2003 to demonstrate. New compact final focus region rf Structures: Optimum cost for 70 MV/m gradient, but deterioration of accelerating structure surfaces seen (at high group velocity). Active R&D this year has made good progress to fix this. Going to low group velocity travelling wave (or standing wave) seems to cure the problem. If need to reduce to 50 MV/m, cost penalty is 5 -10%. Cost: estimate $3. 7 B with manpower (no escalation, contingency, detectors, FY 2000$ ). Injectors: 19%; global costs: 17%; Linacs: 39%; beam delivery: 11%; management/business: 14%
9 Main LC physics themes Precision measurements in the past decade (LEP, SLC, Tevatron, n scattering) indicate the need for something like the Higgs boson below a few 100 Ge. V. Study the `Higgs boson’ (or its surrogate) and understand what it really is. The SM Higgs mechanism is unstable and ugly. We expect some new physics beyond the SM to occur at the Te. V scale Find and explore this new physics sector. (Also a rich program of study of the top quark, QCD, precision EW measurements, etc. ) Recent comprehensive physics studies: TESLA TDR, DESY 2001 – 011, (Part III – Physics at an e+e- Linear Collider) LC Physics : Resource Book for Snowmass 2001, (hep-ex/0106055, 056, 057, 058) ACFA Physics Book: http: //acfahep. kek. jp
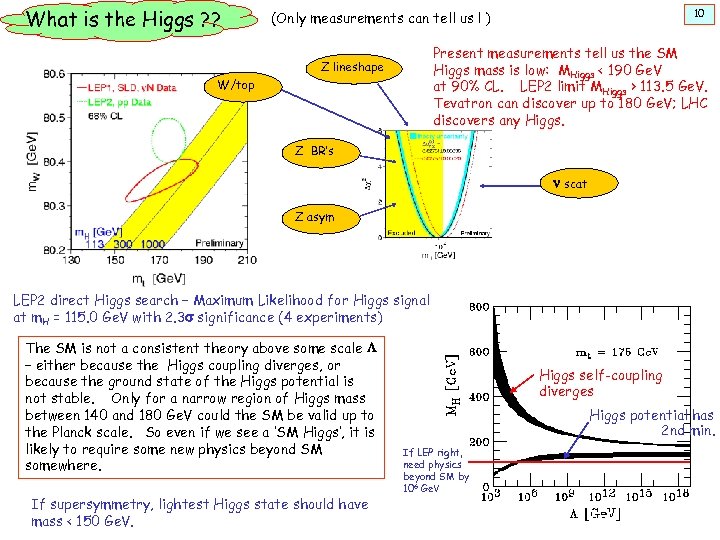What is the Higgs ? ? 10 (Only measurements can tell us ! ) Present measurements tell us the SM Higgs mass is low: MHiggs < 190 Ge. V at 90% CL. LEP 2 limit MHiggs > 113. 5 Ge. V. Tevatron can discover up to 180 Ge. V; LHC discovers any Higgs. Z lineshape W/top Z BR’s n scat Z asym LEP 2 direct Higgs search – Maximum Likelihood for Higgs signal at m. H = 115. 0 Ge. V with 2. 3 s significance (4 experiments) The SM is not a consistent theory above some scale L – either because the Higgs coupling diverges, or because the ground state of the Higgs potential is not stable. Only for a narrow region of Higgs mass between 140 and 180 Ge. V could the SM be valid up to the Planck scale. So even if we see a ‘SM Higgs’, it is likely to require some new physics beyond SM somewhere. If supersymmetry, lightest Higgs state should have mass < 150 Ge. V. Higgs self-coupling diverges Higgs potential has 2 nd min. If LEP right, need physics beyond SM by 106 Ge. V
Program for Higgs Study 11 Find a Higgs boson candidate, and measure its mass (& masses of added Higgs states in SM extensions) Tevatron or LHC should discover Higgs, and measure the mass well dominantly in invisible modes – but then the LC finds it). (unless Higgs decays Measure total width, GTOT, and couplings to all available fermion pairs and gauge bosons. Are the couplings proportional to mass? Do they conform to the simple SM? or to Susy models? Is there more than 1 Higgs? LHC will not do GTOT (or do rather poorly) and only ratios of some couplings to ~20%. Linear Collider can measure G and couplings to ~5%; these are crucial to establish the nature of the Higgs. Measure the quantum numbers of the Higgs states. For the SM, expect JPC = 0++ ; for Susy, both 0++ and 0 -+ (strong coupling: 0 -+ ). LHC will not do; Linear Collider will do easily Explore the Higgs potential. The self-couplings lead to multiple Higgs production. LHC will not do; LC can do trilinear coupling, with sufficient luminosity Tevatron/LHC should discover a Higgs candidate; LC should discover what it really is. We will likely need both !
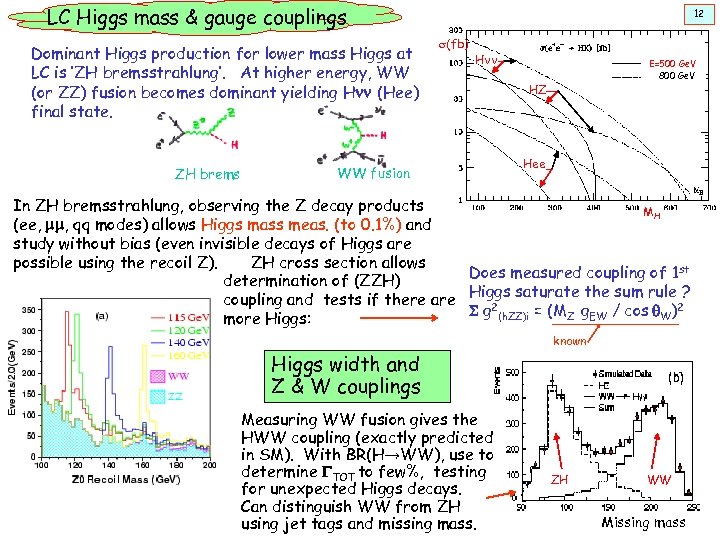LC Higgs mass & gauge couplings Dominant Higgs production for lower mass Higgs at LC is ‘ZH bremsstrahlung’. At higher energy, WW (or ZZ) fusion becomes dominant yielding Hnn (Hee) final state. ZH brems 12 s(fb) Hnn WW fusion E=500 Ge. V 800 Ge. V HZ Hee In ZH bremsstrahlung, observing the Z decay products MH (ee, mm, qq modes) allows Higgs mass meas. (to 0. 1%) and study without bias (even invisible decays of Higgs are possible using the recoil Z). ZH cross section allows Does measured coupling of 1 st determination of (ZZH) Higgs saturate the sum rule ? coupling and tests if there are S g 2(h. ZZ)i = (MZ g. EW / cos q. W)2 more Higgs: known Higgs width and Z & W couplings Z recoil mass Measuring WW fusion gives the HWW coupling (exactly predicted in SM). With BR(H→WW), use to determine GTOT to few%, testing for unexpected Higgs decays. Can distinguish WW from ZH using jet tags and missing mass. ZH Missing mass WW Missing mass
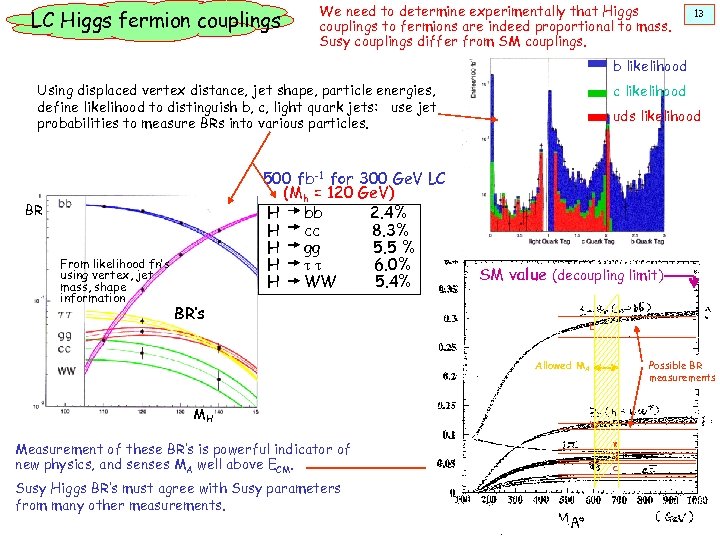LC Higgs fermion couplings We need to determine experimentally that Higgs couplings to fermions are indeed proportional to mass. Susy couplings differ from SM couplings. 13 b likelihood Using displaced vertex distance, jet shape, particle energies, define likelihood to distinguish b, c, light quark jets: use jet probabilities to measure BRs into various particles. 500 fb-1 for 300 Ge. V LC (Mh = 120 Ge. V) H bb 2. 4% H cc 8. 3% H gg 5. 5 % H tt 6. 0% H WW 5. 4% BR From likelihood fn’s using vertex, jet mass, shape information BR’s c likelihood uds likelihood SM value (decoupling limit) b Possible BR measurements Allowed MA MH Measurement of these BR’s is powerful indicator of new physics, and senses MA well above ECM. Susy Higgs BR’s must agree with Susy parameters from many other measurements. W t g c
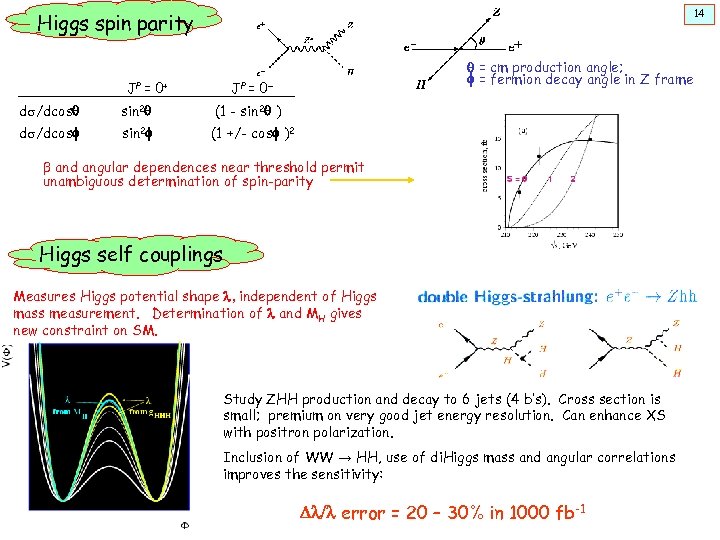14 Higgs spin parity JP = 0 + q = cm production angle; f = fermion decay angle in Z frame JP = 0 - ds/dcosq sin 2 q (1 - sin 2 q ) ds/dcosf sin 2 f (1 +/- cosf )2 b and angular dependences near threshold permit unambiguous determination of spin-parity Higgs self couplings Measures Higgs potential shape l, independent of Higgs mass measurement. Determination of l and MH gives new constraint on SM. Study ZHH production and decay to 6 jets (4 b’s). Cross section is small; premium on very good jet energy resolution. Can enhance XS with positron polarization. Inclusion of WW → HH, use of di. Higgs mass and angular correlations improves the sensitivity: Dl/l error = 20 – 30% in 1000 fb-1
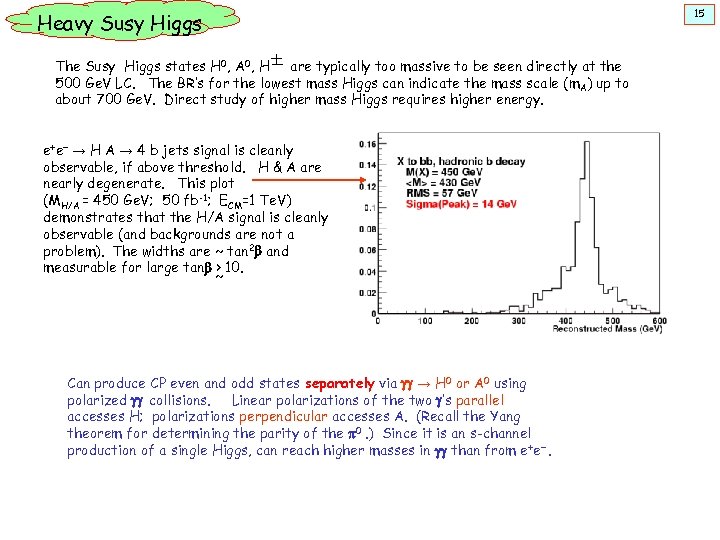Heavy Susy Higgs The Susy Higgs states H 0, A 0, H are typically too massive to be seen directly at the 500 Ge. V LC. The BR’s for the lowest mass Higgs can indicate the mass scale (m. A) up to about 700 Ge. V. Direct study of higher mass Higgs requires higher energy. e+e- → H A → 4 b jets signal is cleanly observable, if above threshold. H & A are nearly degenerate. This plot (MH/A = 450 Ge. V; 50 fb-1; ECM=1 Te. V) demonstrates that the H/A signal is cleanly observable (and backgrounds are not a problem). The widths are ~ tan 2 b and measurable for large tanb > 10. ~ Can produce CP even and odd states separately via gg → H 0 or A 0 using polarized gg collisions. Linear polarizations of the two g’s parallel accesses H; polarizations perpendicular accesses A. (Recall the Yang theorem for determining the parity of the p 0. ) Since it is an s-channel production of a single Higgs, can reach higher masses in gg than from e+e-. 15
Physics beyond the Standard Model There are serious defects of the SM: No gauge interaction unification occurs Higgs mass is unstable to loop corrections Can’t explain baryon asymmetry in universe … Many possible new theories are proposed to cure these ills and embed the SM in a larger framework: Supersymmetry Susy models come in many variants, with different scales of Susy breaking (supergravity, gauge mediation, anomaly mediation … ) Each has a different spectrum of particles, underlying parameters. A new gauge interaction like QCD with `mesons’ at larger masses. (Technicolor/topcolor) These ‘Strong Coupling’ models avoid introducing a fundamental scalar. `Technipions’ play the role of Higgs; there are new particles to be observed, and modifications to WW scattering. String-inspired models with some extra dimensions compactified at millimeter to femtometer scales. Something different? LC must be able to sort out which is at work. Can imagine cases where LHC sees new phenomena, but misunderstands the source. 16
Supersymmetry If Susy is to stabilize the Higgs & gauge boson masses (and give grand unification) it is ‘natural’ to believe that some Supersymmetric particles will appear at a 500 Ge. V LC. The main goal is to measure the underlying model parameters and from them deduce the character of the supersymmetry breaking and its energy scale. There are ~105 unknown parameters in general Susy model. All should be measured, and used to fix the models. This can be done through measurement of the masses, quantum numbers, branching ratios, asymmetries, CP phases -- and in particular the pattern of mixing of states with similar quantum numbers -- the 2 stops, sbottoms, staus, and the 2 chargino and 4 neutralino states (partners of the g/Z/W and supersymmetric Higgs states). Susy may well be the next frontier for flavor physics – study FCNC, CP violation for sparticles, generational patterns, etc. Susy can provide a dark matter candidate (the lightest neutralino). Susy can provide the CP phases that enables the baryon-antibaryon asymmetry The LHC will discover Susy if it exists. But disentangling the information on the full mass spectrum, particle quantum #s, couplings and the mixings will be difficult at LHC. The LC can make these crucial measurements, benefiting from: Polarization of electron (positron? ) beam Known partonic cm energy Known initial state (JP = 1 - ) (to the extent that the states are accessible) 17
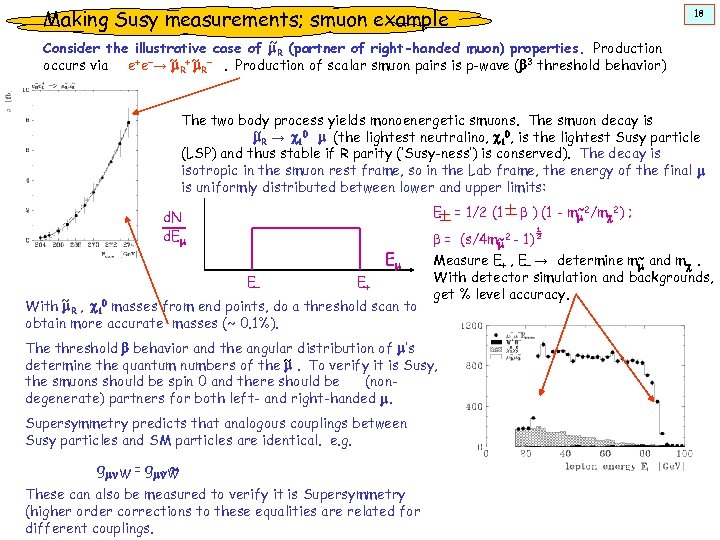Making Susy measurements; smuon example 18 Consider the illustrative case of ~R (partner of right-handed muon) properties. Production m +e-→ ~ + ~ -. Production of scalar smuon pairs is p-wave (b 3 threshold behavior) occurs via e m. R The two body process yields monoenergetic smuons. The smuon decay is ~ → c 0 m (the lightest neutralino, c 0, is the lightest Susy particle m. R 1 1 (LSP) and thus stable if R parity (‘Susy-ness’) is conserved). The decay is isotropic in the smuon rest frame, so in the Lab frame, the energy of the final m is uniformly distributed between lower and upper limits: E = 1/2 (1 d. N d. Em Em E- E+ With ~ R , c 10 masses from end points, do a threshold scan to m obtain more accurate masses (~ 0. 1%). b = (s/4 m~2 - 1) ½ m Measure E+ , E- → determine m~ and mc. m With detector simulation and backgrounds, get % level accuracy. The threshold b behavior and the angular distribution of m’s determine the quantum numbers of the ~. To verify it is Susy, m the smuons should be spin 0 and there should be (nondegenerate) partners for both left- and right-handed m. Supersymmetry predicts that analogous couplings between Susy particles and SM particles are identical. e. g. gmn. W = gmn. W ~~ These can also be measured to verify it is Supersymmetry (higher order corrections to these equalities are related for different couplings. b ) (1 - m~2/mc 2) ; m
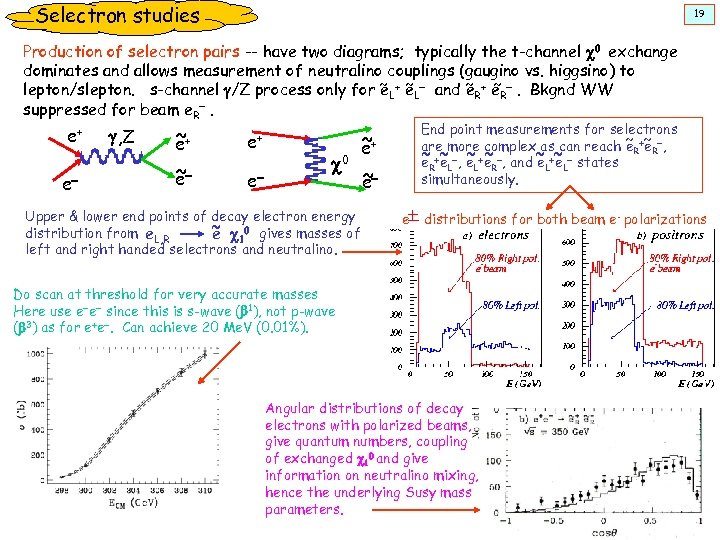Selectron studies 19 Production of selectron pairs -- have two diagrams; typically the t-channel c 0 exchange dominates and allows measurement of neutralino couplings (gaugino vs. higgsino) to lepton/slepton. s-channel g/Z process only for ~ L+ e. L- and ~ R+ e. R-. Bkgnd WW e ~ suppressed for beam e. R-. e+ e- g, Z ~ e+ e+ ~ e- e- c 0 Upper & lower end points of decay electron energy ~ c 0 gives masses of distribution from e. L, R e 1 left and right handed selectrons and neutralino. ~ e+ ~e End point measurements for selectrons are more complex as can reach ~R+~R-, e e ~ +~ -, e +e -, and ~ +~ - states ~ ~ e. R e. L L R e. L simultaneously. e distributions for both beam e- polarizations Do scan at threshold for very accurate masses Here use e-e- since this is s-wave (b 1), not p-wave (b 3) as for e+e-. Can achieve 20 Me. V (0. 01%). Angular distributions of decay electrons with polarized beams, give quantum numbers, coupling of exchanged c 10 and give information on neutralino mixing, hence the underlying Susy mass parameters.
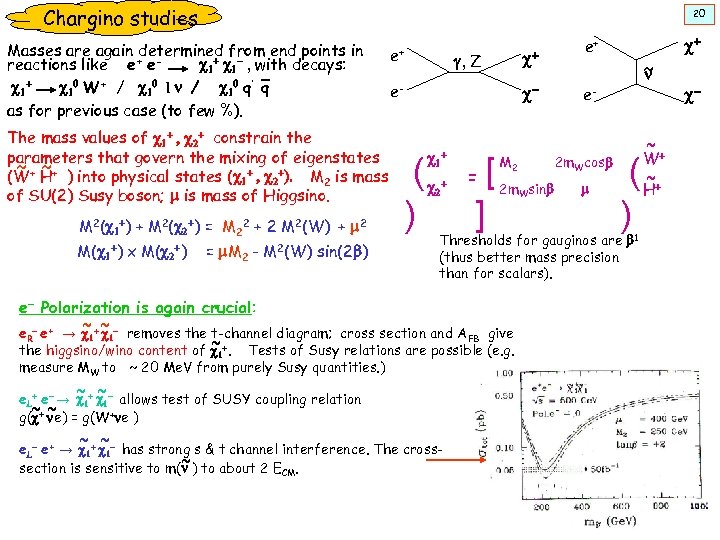Chargino studies 20 Masses are again determined from end points in reactions like e+ ec 1+ c 1 - , with decays: c 1+ c 10 W+ / c 10 l n / c 10 q’ q as for previous case (to few %). The mass values of c 1+ , c 2+ constrain the parameters that govern the mixing of eigenstates ~ ~ (W+ H+ ) into physical states (c 1+ , c 2+). M 2 is mass of SU(2) Susy boson; m is mass of Higgsino. M 2(c 1+) + M 2(c 2+) = M 22 + 2 M 2(W) + m 2 M(c 1+) x M(c 2+) = m. M 2 - M 2(W) sin(2 b) e+ c+ g, Z e- cc 1+ (c ) + 2 [ = ] M 2 2 m. Wsinb ~ n e- 2 m. Wcosb m ( ) Thresholds for gauginos are b 1 (thus better mass precision than for scalars). e- Polarization is again crucial: ~ ~ e. R- e+ → c 1+ c 1 - removes the t-channel diagram; cross section and A FB give ~ the higgsino/wino content of c +. Tests of Susy relations are possible (e. g. 1 measure MW to ~ 20 Me. V from purely Susy quantities. ) e. L+ e- → ~1+ c 1 - allows test of SUSY coupling relation c ~ ~ ~ g(c+ ne) = g(W+ne ) ~ ~ e+ e. L- e+ → c 1+ c 1 - has strong s & t channel interference. The cross~ section is sensitive to m(n ) to about 2 ECM. ~ W+ ~ H+ c+ c-
Neutralino studies 21 ~ ~ The mass matrix for the 4 J= ½ neutral gauginos (b, w 3, H 1, H 2) depends on the U(1), SU(2) gaugino masses M 1, M 2, the higgsino mass parameter m and tanb. The mass matrix can be diagonalized to give the physical ~i 0 states (i=1, 4). There are 14 possible CP violating phases in the c neutralino sector alone (46 overall in MSSM). Unitarity relations yield unitarity quadrangles which in principle can be determined experimentally, through a combination of neutralino production cross sections, and fermion-sfermion-neutralino vertix determinations. These, together with the chargino measurents, make it possible to extract the underlying Susy parameters even in the case of CP violation. We need to know |M 1|ei. F 1, M 2, |m|ei. Fm, tanb to fix the low energy Susy model. m(c 10) ~ ~ ~ c Measurement of c 1+ c 1 - and c 1+ ~ 2 - XS’s with polarized beams give us M 2, mei. Fm, tanb ~ ~ Measurement of c 10 and c 20 masses and ~ ~ s(c 10 c 20) then give |M 1| and its phase Fm CP violating observables like → ·(p+ x→-) in reaction e+e- → ~ 10~ 20 → ~ 10 l +l pe → p c c can directly signal CP violation. m(c 20)
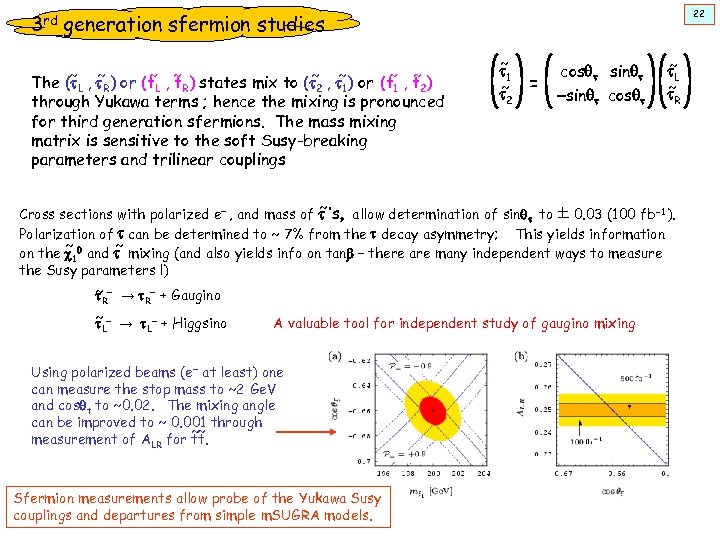22 3 rd generation sfermion studies ~ ~ ~ ~ The (t. L , t. R) or (t. L , t. R) states mix to (t 2 , t 1) or (t 1 , t 2) through Yukawa terms ; hence the mixing is pronounced for third generation sfermions. The mass mixing matrix is sensitive to the soft Susy-breaking parameters and trilinear couplings ~ t 1 ~ t 2 = cosqt sinqt -sinqt cosqt ~ t. L ~ t. R ~ Cross sections with polarized e- , and mass of t ’s, allow determination of sinqt to 0. 03 (100 fb-1). Polarization of t can be determined to ~ 7% from the t decay asymmetry; This yields information ~ ~ on the c 10 and t mixing (and also yields info on tanb – there are many independent ways to measure the Susy parameters !) ~ - → t - + Gaugino t R R ~ - → t - + Higgsino t. L L A valuable tool for independent study of gaugino mixing Using polarized beams (e- at least) one can measure the stop mass to ~2 Ge. V and cosqt to ~0. 02. The mixing angle can be improved to ~ 0. 001 through ~~ measurement of ALR for tt. Sfermion measurements allow probe of the Yukawa Susy couplings and departures from simple m. SUGRA models.
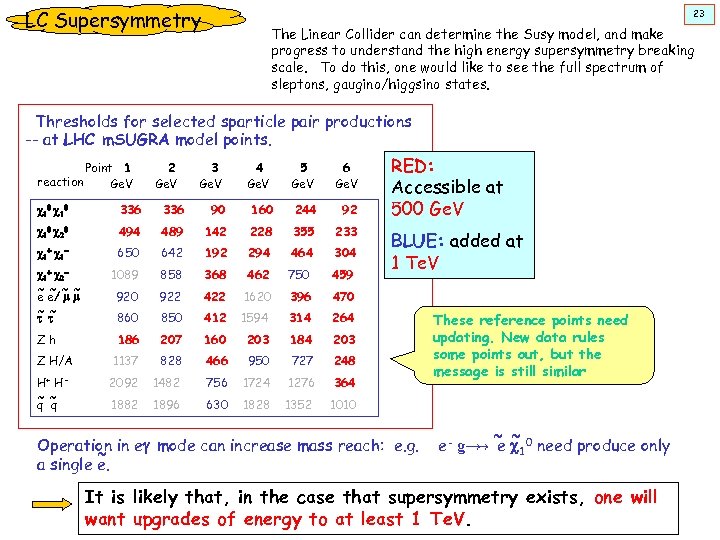LC Supersymmetry 23 The Linear Collider can determine the Susy model, and make progress to understand the high energy supersymmetry breaking scale. To do this, one would like to see the full spectrum of sleptons, gaugino/higgsino states. Thresholds for selected sparticle pair productions -- at LHC m. SUGRA model points. Point 1 reaction Ge. V 2 Ge. V 3 Ge. V 4 Ge. V 5 Ge. V 6 Ge. V c 10 336 90 160 244 92 c 10 c 20 494 489 142 228 355 233 c 1+ c 1 - 650 642 192 294 464 304 1089 858 368 462 750 459 920 922 422 1620 396 470 860 850 412 1594 314 264 186 207 160 203 184 203 Z H/A 1137 828 466 950 727 248 H+ H ~ ~ q q 2092 1482 756 1724 1276 364 1882 1896 630 1828 1352 RED: Accessible at 500 Ge. V 1010 c 1+ c 2~ ~ e e/ m m ~ ~ t t Zh BLUE: added at 1 Te. V Operation in eg mode can increase mass reach: e. g. ~ a single e. These reference points need updating. New data rules some points out, but the message is still similar ~ ~ e- g→ e c 10 need produce only → It is likely that, in the case that supersymmetry exists, one will want upgrades of energy to at least 1 Te. V.
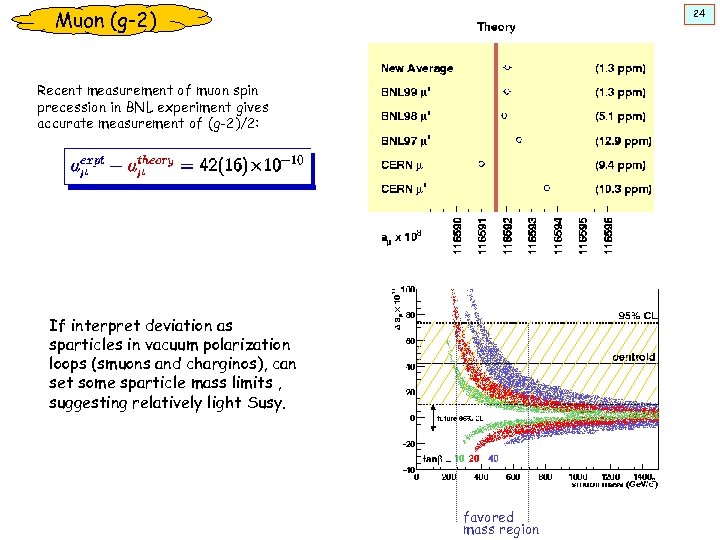Muon (g-2) 24 Recent measurement of muon spin precession in BNL experiment gives accurate measurement of (g-2)/2: If interpret deviation as sparticles in vacuum polarization loops (smuons and charginos), can set some sparticle mass limits , suggesting relatively light Susy. favored mass region
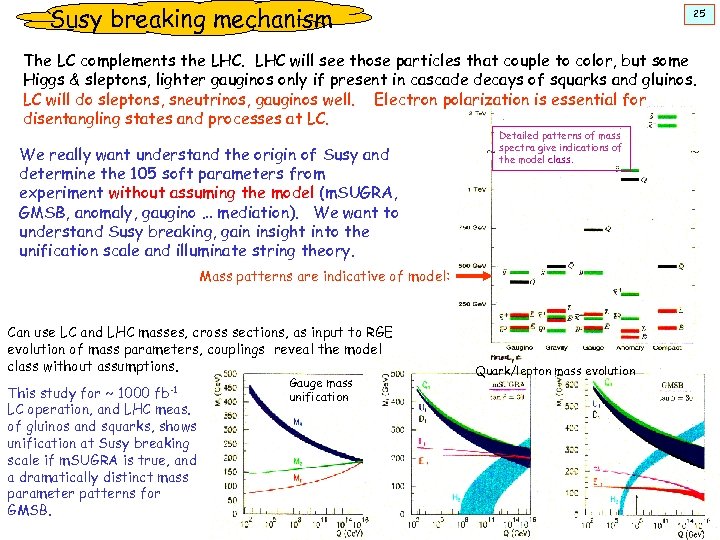Susy breaking mechanism 25 The LC complements the LHC will see those particles that couple to color, but some Higgs & sleptons, lighter gauginos only if present in cascade decays of squarks and gluinos. LC will do sleptons, sneutrinos, gauginos well. Electron polarization is essential for disentangling states and processes at LC. We really want understand the origin of Susy and determine the 105 soft parameters from experiment without assuming the model (m. SUGRA, GMSB, anomaly, gaugino … mediation). We want to understand Susy breaking, gain insight into the unification scale and illuminate string theory. Detailed patterns of mass spectra give indications of the model class. Mass patterns are indicative of model: Can use LC and LHC masses, cross sections, as input to RGE evolution of mass parameters, couplings reveal the model class without assumptions. This study for ~ 1000 fb-1 LC operation, and LHC meas. of gluinos and squarks, shows unification at Susy breaking scale if m. SUGRA is true, and a dramatically distinct mass parameter patterns for GMSB. Gauge mass unification Quark/lepton mass evolution
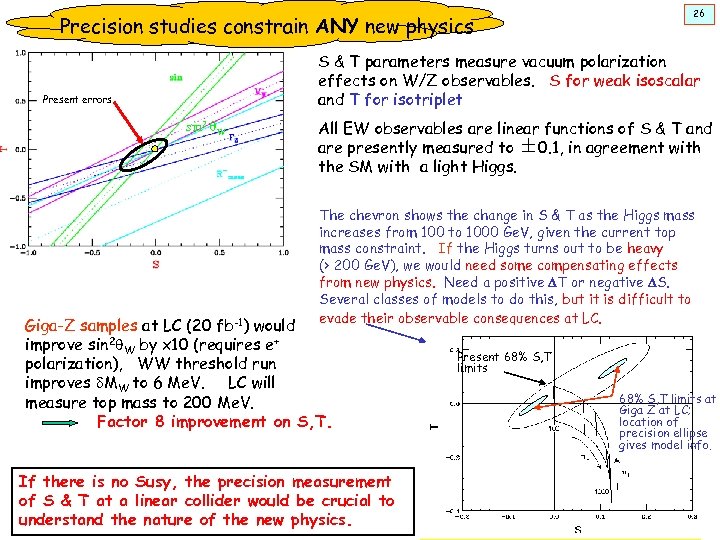Precision studies constrain ANY new physics 26 S & T parameters measure vacuum polarization effects on W/Z observables. S for weak isoscalar and T for isotriplet Present errors sin 2 q. W All EW observables are linear functions of S & T and are presently measured to 0. 1, in agreement with the SM with a light Higgs. The chevron shows the change in S & T as the Higgs mass increases from 100 to 1000 Ge. V, given the current top mass constraint. If the Higgs turns out to be heavy (> 200 Ge. V), we would need some compensating effects from new physics. Need a positive DT or negative DS. Several classes of models to do this, but it is difficult to evade their observable consequences at LC. Giga-Z samples at LC (20 fb-1) would improve sin 2 q. W by x 10 (requires e+ polarization), WW threshold run improves d. MW to 6 Me. V. LC will measure top mass to 200 Me. V. Factor 8 improvement on S, T. If there is no Susy, the precision measurement of S & T at a linear collider would be crucial to understand the nature of the new physics. Present 68% S, T limits at Giga Z at LC; location of precision ellipse gives model info.
Precision measurements In the case that the LHC/LC does not see supersymmetry, precision EW measurements will have added importance as signposts to the new physics. NLC design has special lower energy collision point – at present alternate HI to LO energy operation, but it may be possible to design concurrent usage with same HI energy IP rep rate. Tesla design would simply lower ECM at the single IP with consequent loss of luminosity. Giga Z: Modest luminosity (20 fb-1 – equivalent in time to ~100 fb-1 at full energy) needed for 109 Z’s. To get the improved Z-pole precisions, need very accurate control of polarization (e. g. for ALR). This could be achieved by using both electron and positron polarization, but the positron polarization schemes are not yet mature. R&D on polarimetry and positron polarization is needed. Even larger Z samples (1010) would become very interesting for precision studies of b-quark couplings, asymmetries, rare decays and would extend b-physics into new regimes. W mass: Scan the cross-section at WW threshold; with 100 fb-1 can get precision ~5 Me. V. Knowing the beam energy and luminosity to the required precision is a challenge (50 ppm on Ebeam). The scan would also give GW to ~ 4 Me. V. Top quark: Scan at tt threshold is sensitive to mt, a. S, Gt and the top Yukawa coupling lt. (lt is also accessible from s(tt. H) at higher energy LC operation. ) With 300 fb-1 at the tt threshold, estimate precisions of: dmt = 18 Me. V; da. S=0. 0015; d. Gt=32 Me. V. Determination of top Yukawa coupling from threshold scan seems limited to about 30%. 27
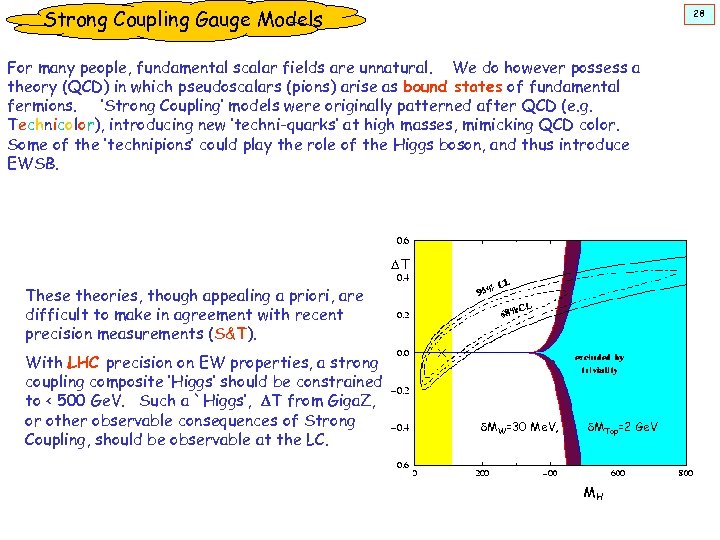Strong Coupling Gauge Models 28 For many people, fundamental scalar fields are unnatural. We do however possess a theory (QCD) in which pseudoscalars (pions) arise as bound states of fundamental fermions. ‘Strong Coupling’ models were originally patterned after QCD (e. g. Technicolor), introducing new ‘techni-quarks’ at high masses, mimicking QCD color. Some of the ‘technipions’ could play the role of the Higgs boson, and thus introduce EWSB. DT These theories, though appealing a priori, are difficult to make in agreement with recent precision measurements (S&T). With LHC precision on EW properties, a strong coupling composite ‘Higgs’ should be constrained to < 500 Ge. V. Such a `Higgs’, DT from Giga. Z, or other observable consequences of Strong Coupling, should be observable at the LC. d. MW=30 Me. V, d. MTop=2 Ge. V MH
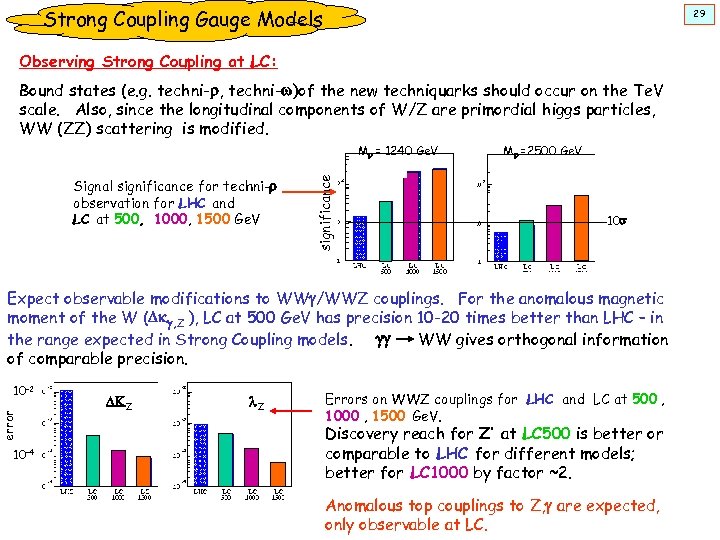Strong Coupling Gauge Models 29 Observing Strong Coupling at LC: Bound states (e. g. techni-r, techni-w)of the new techniquarks should occur on the Te. V scale. Also, since the longitudinal components of W/Z are primordial higgs particles, WW (ZZ) scattering is modified. Signal significance for techni-r observation for LHC and LC at 500, 1000, 1500 Ge. V significance Mr = 1240 Ge. V M r =2500 Ge. V 10 s Expect observable modifications to WWg/WWZ couplings. For the anomalous magnetic moment of the W (Dkg, Z ), LC at 500 Ge. V has precision 10 -20 times better than LHC – in the range expected in Strong Coupling models. gg WW gives orthogonal information of comparable precision. error 10 -2 10 -4 DKZ l. Z Errors on WWZ couplings for LHC and LC at 500 , 1000 , 1500 Ge. V. Discovery reach for Z’ at LC 500 is better or comparable to LHC for different models; better for LC 1000 by factor ~2. Anomalous top couplings to Z, g are expected, only observable at LC.
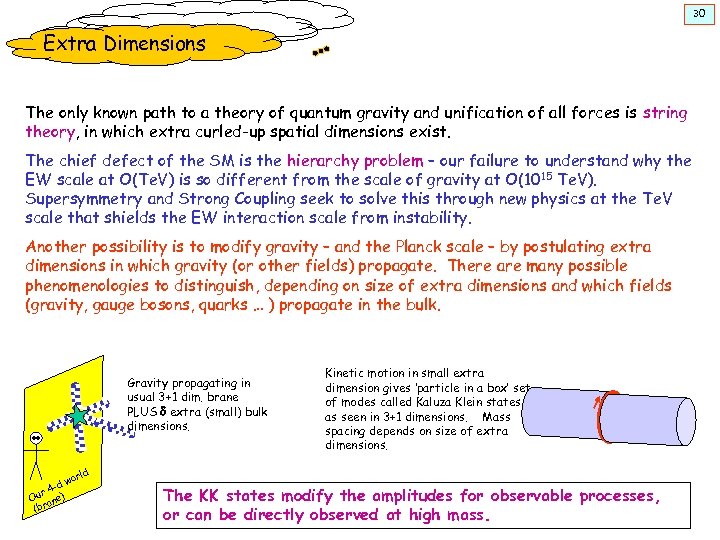30 Extra Dimensions The only known path to a theory of quantum gravity and unification of all forces is string theory, in which extra curled-up spatial dimensions exist. The chief defect of the SM is the hierarchy problem – our failure to understand why the EW scale at O(Te. V) is so different from the scale of gravity at O(1015 Te. V). Supersymmetry and Strong Coupling seek to solve this through new physics at the Te. V scale that shields the EW interaction scale from instability. Another possibility is to modify gravity – and the Planck scale – by postulating extra dimensions in which gravity (or other fields) propagate. There are many possible phenomenologies to distinguish, depending on size of extra dimensions and which fields (gravity, gauge bosons, quarks … ) propagate in the bulk. Gravity propagating in usual 3+1 dim. brane PLUS d extra (small) bulk dimensions. -d r 4 Ou ane) (br Kinetic motion in small extra dimension gives ‘particle in a box’ set of modes called Kaluza Klein states as seen in 3+1 dimensions. Mass spacing depends on size of extra dimensions. rld wo The KK states modify the amplitudes for observable processes, or can be directly observed at high mass.
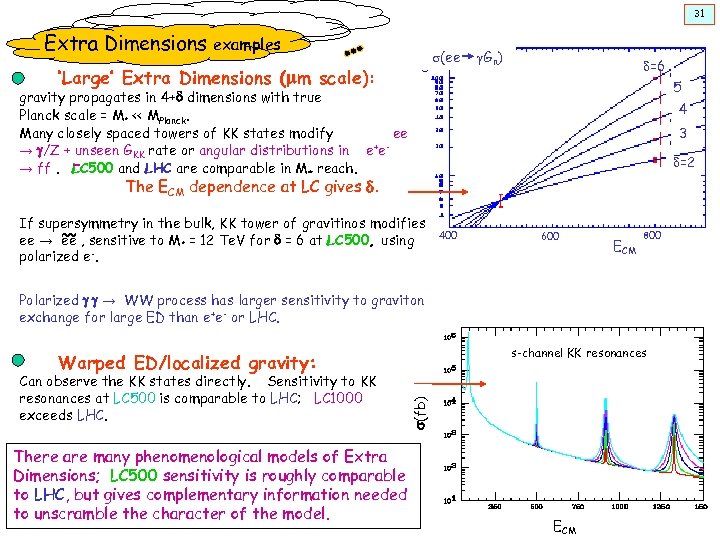31 Extra Dimensions examples s(ee ‘Large’ Extra Dimensions (mm scale): g. Gn) d=6 5 gravity propagates in 4+d dimensions with true Planck scale = M* << MPlanck. Many closely spaced towers of KK states modify ee + e→ g/Z + unseen GKK rate or angular distributions in e → ff. LC 500 and LHC are comparable in M* reach. 4 3 d=2 The ECM dependence at LC gives d. If supersymmetry in the bulk, KK tower of gravitinos modifies ~ ~ ee → ee , sensitive to M* = 12 Te. V for d = 6 at LC 500, using polarized e-. 400 600 ECM 800 Polarized g g → WW process has larger sensitivity to graviton exchange for large ED than e+e- or LHC. s-channel KK resonances Can observe the KK states directly. Sensitivity to KK resonances at LC 500 is comparable to LHC; LC 1000 exceeds LHC. There are many phenomenological models of Extra Dimensions; LC 500 sensitivity is roughly comparable to LHC, but gives complementary information needed to unscramble the character of the model. s(fb) Warped ED/localized gravity: ECM
Scenarios Are there physics scenarios for which the LC does not add critical information beyond LHC? Have looked at many possible physics situations, including cases where low scale supersymmetry does not exist, or the Higgs is at unexpectedly high mass. v Do not see a plausible case where the LC cannot find and study the Higgs, though it is possible that one would need a bit more than 500 Ge. V in extreme strong coupling models. In the case of MH > 200 Ge. V, where H → WW predominantly (e. g. in strong coupling models), one would learn less about the Higgs sector (no observable fermionic couplings), but still significantly more than at LHC. v If there is Susy, the LC should be the instrument of choice for its study – but going to higher energy ultimately to see all the states would be very desirable. v If there is no Susy (Strong Coupling or Extra Dimensions), the LC will add information not available from the LHC. In these cases, the Giga-Z option may be crucial, as the constraints from precision measurements on the new physics will be very important. In the most extreme (and unexpected) case of no Higgs and no new physics, the LC precision measurements will be a critical need to point the way to this non-SM situation. In the case that the physics menu at the LC is very rich, one may ask how long it may take to obtain reasonable precision for all the measureables of interest – how much luminosity at each of the several energy settings, beam polarizations, and different beam particles (e+ e-, e- g and g g). This bears upon setting a benchmark for the luminosity of the collider. 32
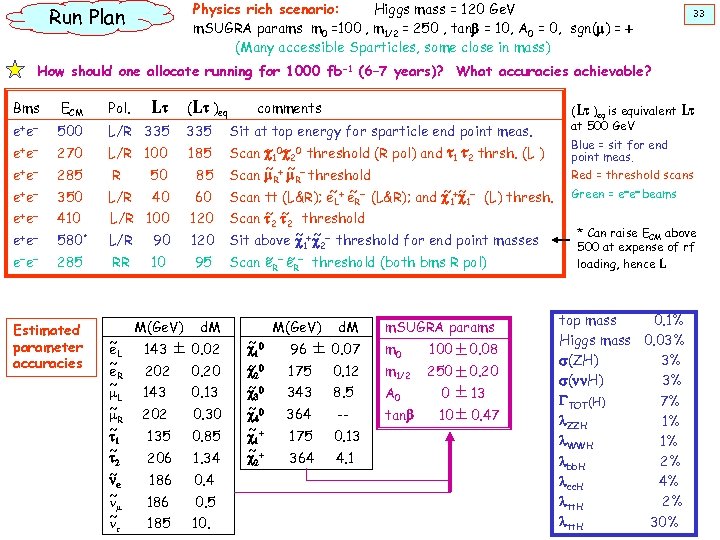Physics rich scenario: Higgs mass = 120 Ge. V m. SUGRA params m 0 =100 , m 1/2 = 250 , tanb = 10, A 0 = 0, sgn(m) = + (Many accessible Sparticles, some close in mass) Run Plan 33 How should one allocate running for 1000 fb-1 (6– 7 years)? What accuracies achievable? Lt (Lt )eq Bms ECM Pol. e+ e- 500 L/R 335 e+ e- 270 L/R 100 185 e+ e- 285 R 50 85 e+ e- 350 L/R 40 60 e+ e- 410 L/R 100 120 e+ e- 580* L/R 90 120 e- e- 285 RR 10 95 Estimated parameter accuracies ~ e. L ~ e. R ~ m. L ~ m. R ~ t 1 ~ t 2 ~ ne ~ n m ~ nt M(Ge. V) d. M 143 0. 02 202 0. 20 143 0. 13 202 0. 30 135 0. 85 206 1. 34 186 0. 5 185 10. comments Sit at top energy for sparticle end point meas. ~ ~ Scan c 10 c 20 threshold (R pol) and ~1 ~2 thrsh. (L ) t t ~ ~ Scan m + m - threshold R R ~ ~ ~ c Scan tt (L&R); e. L+ e. R- (L&R); and c 1+~1 - (L) thresh. ~ ~ Scan t t threshold 2 2 ~ ~ Sit above c 1+c 2 - threshold for end point masses ~ ~ Scan e - threshold (both bms R pol) R ~ c 10 ~ c 20 ~ c 0 3 ~ c 40 ~ c 1+ ~ c 2+ R M(Ge. V) d. M 96 0. 07 175 0. 12 343 8. 5 364 -- 175 0. 13 364 4. 1 m. SUGRA params m 0 100 0. 08 m 1/2 250 0. 20 A 0 0 13 tanb 10 0. 47 (Lt )eq is equivalent at 500 Ge. V Lt Blue = sit for end point meas. Red = threshold scans Green = e-e- beams * Can raise ECM above 500 at expense of rf loading, hence L top mass 0. 1% Higgs mass 0. 03% s(ZH) 3% s(nn. H) 3% GTOT(H) 7% l. ZZH 1% l. WWH 1% lbb. H 2% lcc. H 4% ltt. H 2% ltt. H 30%
Realizing a Linear Collider 34 Recent studies assessed the priority of future new projects in Europe (ECFA), Asia (ACFA) and the US (HEPAP) all concluded resoundingly that the LC was the highest priority for a next step. Ø Expect technical proposals and proposals to site a LC from each of the three regions. The TESLA proposal is now before the German Science Ministry, with a recommendation expected in 2002. Ø Ø The cost of the LC will be high – multi B$. Will be no more than one LC in the world ! There is an international committee charged by ICFA evaluating the technical merits, comparative costs, and R&D issues – report in late 2002? (but is not a decision making body!) Ø Setting the organizational structure will be critical. ‘LHC’ model = a host country with major control & funding and contributing partners vs. ‘CERN’ model = collaboration of more equal partners ? Ø The choice of site will be difficult; it will likely be driven by the region that is willing to put up the majority of the funding ( 1/2 → 2/3 ? ). Need international discussion to start now; ICFA seems the appropriate body to charge this; Ø define the model for the organizational structure; should it be LC specific? or aimed at future cooperative facilities across the world? (‘super CERN’? ) Ø how will a site decision be reached? Ø establish mechanism for reaching a technical decision (TESLA vs. NLC); Ø establish a rough timeline for actions, decisions Ø how autonomous should responsibilities be ? (e. g. injectors ; main linac; IR’s by separate regions, soup to nuts) Ø how to involve governmental bodies in the process now Ø what materials needed to make the case to other scientists, governments? ( “why not wait for LHC results? ” ) HEP has pioneered such collaboration on the smaller scale of collider detectors in the past. We can help establish the paradigm for future international scientific cooperation.
Summary A Linear Collider, starting at 500 Ge. V and expanding to higher energy, will bring crucial understanding of the main questions before our field, significantly beyond that obtained at LHC. It should provide definitive understanding of Electroweak Symmetry Breaking, and may give insights into questions such as dark matter, CP violation & the role of flavor. A Linear Collider is technically challenging and expensive; it can only be achieved through international cooperation.