P C Pandey EE Dept IIT Bombay National

P. C. Pandey, EE Dept, IIT Bombay National Seminar on the Recent Developments in Circuits, Signals and Signal Processing (RDCSSP-2011), St Francis Institute of Technology, Mumbai, 23 -24 Feb 2011 Estimation of Vocal Tract Shape from Speech Signal P. C. Pandey EE Dept, IIT Bombay <pcpandey AT ee. iitb. ac. in > http: www. ee. iitb. ac. in/~pcpandey ♠♠ ►► 1. Intro. 2. Visual STA / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay P. C. Pandey, “Estimation of vocal tract shape from speech signal ”, National Seminar on the Recent Developments in Circuits, Signals and Signal Processing (RDCSSP-2011), St Francis Institute of Technology, Mumbai, 23 -24 Feb 2011 Abstract -- Children with hearing impairment lack auditory feedback and have great difficulty in acquiring speech. Most of them do not learn to speak properly despite a fully functional speech production system. Speech-training systems providing visual feedback of vocal-tract shape are found to be useful for improving vowel articulation. Processing of speech signal using linear predictive coding (LPC) and other analysis techniques, with appropriate selection of analysis parameters, can be used for estimating the vocal tract shape during vowels and semivowels. The estimation of the shape from the speech signal generally fails during stop closures, and this restricts its effectiveness in speech training for production of consonants not having visible articulatory efforts. A technique based on two-dimensional surface modeling of the area values, estimated by LPC analysis, during the vowel-consonant and consonant-vowel transitions preceding and following the stop closure, has been investigated for interpolating the area values during the stop closures. Surface modeling was based on least-squares bivariate polynomials. Using the technique, the place of closure could be estimated consistently for various stop consonants and the values obtained are in good agreement with those obtained from direct imaging techniques. The shape obtained by LPC analysis of steady vowels shows variability with the position of the analysis frame. A windowed energy index is calculated as the ratio of the energy of the windowed signal to the frame energy, and it is shown that the shapes in the frames corresponding to the valleys in this index have a reduced variability. Thus the selection of the frames based on this index can be used for improving the consistency of vocal tract shape estimation for various applications. Based on this research and work by others, a PC based visual speech-training system for estimating the vocal tract shape from the speech signal input through the sound card and displaying the dynamic variation in the shape on its monitor with a graphical interface is being developed, with the objective of facilitating various aspects of speech learning by the hearing impaired Intro. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ♠♠ 1. children. ◄◄ ►► 2 / 95

P. C. Pandey, EE Dept, IIT Bombay Bibliography P. C. Pandey & M. S. Shah, “Estimation of place of articulation during stop closures of vowel-consonant-vowel utterances”, IEEE Trans. Audio, Speech, and Language Proc. , vol 17(2), pp 277 -286, Feb. 2009. K. S. Nataraj, Jagbandhu, P. C. Pandey, and M. S. Shah, Improving the consistency of vocal tract shape estimation, Proc. National Conference on Communications 2011 (NCC 2011), Bangalore, India. M. S. Shah, “Estimation of place of articulation during stop closures of vowel-consonant-vowel syllables”, Ph. D. dissertation, EE Dept. , IIT Bombay, 2008. J. F. Curtis (Ed. ), Processes and Disorders of Human Communication. New York: Harper and Row, 1978. R. S. Nikerson, “Characteristics of the speech of deaf persons, ” Volta Rev. , vol. 77, pp. 342– 362, 1975; reprinted in: Sensory Aids for the Hearing Impaired, pp. 540– 545, H. Levitt, J. M. Pickett, and R. A. Houde (Eds. ), New York: IEEE Press, 1980. H. Levitt, J. M. Pickett, and R. A. Houde, (Eds. ), Sensory Aids for the Hearing Impaired. New York: IEEE Press, 1980. R. G. Crichton and F. Fallside, “Linear prediction model of speech production with applications to deaf speech training, ” Proc. IEE Control and Sci. , vol. 121, pp. 865– 873, 1974. J. M. Pardo, “Vocal tract shape analysis for children, ” in Proc. IEEE Int. Conf. Acoust. , Speech, Signal Process. , pp. 763– 766, 1982. S. Aguilera, A. Borrajo, J. M. Pardo, and E. Munoz, “Speech-analysis-based devices for diagnosis and education of speech and hearing impaired people, ” in Proc. IEEE Int. Conf. Acoust. , Speech, Signal Process. , pp. 641– 644, 1986. M. Shigenaga and H. Kubo, “Speech training system for handicapped children using vocal tract lateral shapes, ” in Proc. IEEE Int. Conf. Acoust. , Speech, Signal Process. , pp. 637– 640, 1986. N. D. Black, “Application of vocal tract shapes to vowel production, ” in Proc. 10 th Int. Conf. IEEE Engg. Med. Biol. Soc. , pp. 1535– 1536, 1988. S. H. Park, D. J. Kim, J. H. Lee, and T. S. Yoon, “Integrated speech training system for hearing impaired, ” IEEE Trans. Rehab. Engg. , vol. 2, no. 4, pp. 189– 196, 1994. P. M. T. de Oliveira and M. N. Souza, “Speech aid for the deaf based on a representation of the vocal tract: the vowel module, ” in Proc. 19 th Int. Conf. IEEE Engg. in Med. and Biol. Soc. , pp. 1757– 1759, 1997. H. Wakita, “Direct estimation of the vocal tract shape by inverse filtering of acoustic speech waveforms, ” IEEE Trans. Audio Electroacoust. , vol. 21, no. 5, pp. 417– 427, 1973. H. Wakita, ‘‘Estimation of vocal-tract shapes from acoustical analysis of the speech wave: The state of the art, ’’ IEEE Trans. Acoust. , Speech, Signal Process. , vol. ASSP-27, no. 3, pp. 281 --285, 1979. P. Ladefoged, R. Harshman, L. Goldstein, and L. Rice, “Generating vocal tract shapes from formant frequencies, ” J. Acoust. Soc. Am. , vol. 64, no. 4, pp. 1027– 1035, 1978. D. Rossiter, D. M. Howard, and M. Downes, “A real-time LPC-based vocal tract area display for voice development, ” J. of Voice, vol. 8, no. 4, pp. 314– 319, 1994. Z. Yu and P. C. Ching, “Determination of vocal-tract shapes from formant frequencies based on perturbation theory and interpolation method, ” in Proc. IEEE Int. Conf. Acoust. , Speech, Signal Process. , pp. 369– 372, 1996. J. Schroeter and M. M. Sondhi, “Techniques for estimating vocal-tract shapes from the speech signal, ” IEEE Trans. Speech Audio Process. , vol. 2, no. 1, pt. 2, pp. 133– 150, 1994. L. R. Rabiner and R. W. Schafer, Digital Processing of Speech Signals. Englewood Cliffs, NJ: Prentice-Hall, 1978. D. O’Shaughnessy, Speech Communications: Human and Machines. Reading, Massachusetts: Addison-Wesley, 1987. ♠♠ ►► 1. Intro. 2. Visual STA 3 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay References ▪ P. C. Pandey and M. S. Shah, “Estimation of place of articulation during stop closures of vowel-consonantvowel utterances”, IEEE Trans. Audio, Speech, and Language Proc. , vol 17(2), pp 277 -286, Feb. 2009. ▪ K. S. Nataraj, Jagbandhu, P. C. Pandey, and M. S. Shah, Improving the consistency of vocal tract shape estimation, Proc. National Conference on Communications 2011 (NCC 2011), Bangalore, India. ▪ M. S. Shah, “Estimation of place of articulation during stop closures of vowel-consonant-vowel syllables”, Ph. D. dissertation, EE Dept. , IIT Bombay, India, 2008. ♠♠ ►► 1. Intro. 2. Visual STA 4 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay Presentation Outline 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 5 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 6 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

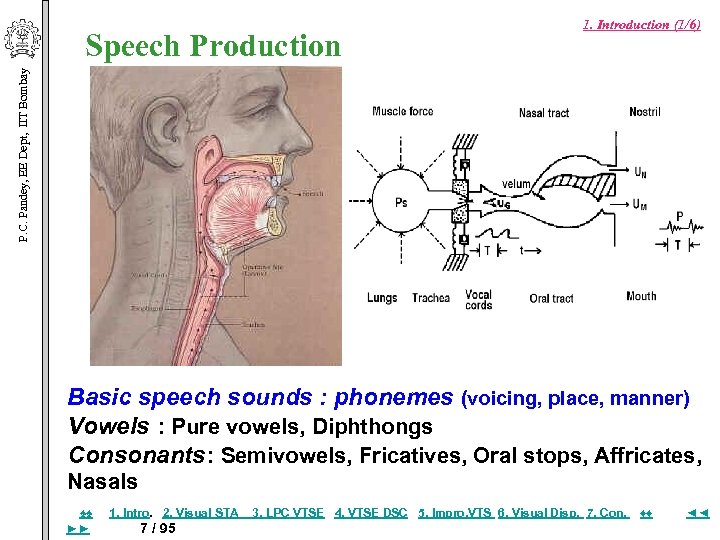
P. C. Pandey, EE Dept, IIT Bombay Speech Production 1. Introduction (1/6) Basic speech sounds : phonemes (voicing, place, manner) Vowels : Pure vowels, Diphthongs Consonants: Semivowels, Fricatives, Oral stops, Affricates, Nasals ♠♠ ►► 1. Intro. 2. Visual STA 7 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction (2/6) Speech Acquisition Process Children with normal hearing Acquisition of ability to control various articulators aided by auditory feedback. Children with hearing impairment Lack of auditory feedback during speech production. Articulation accuracy, stress, & intonation patterns affected. Vowels & consonants with tongue movement hidden in the mouth not distinguishable. Speech impairment, despite proper speech production mechanism. ♠♠ ►► 1. Intro. 2. Visual STA 8 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction (3/6) Speech Training Aids ♦ Visual feedback ♦ Tactile feedback Importance of visual feedback of articulatory gestures Only 20% of the English phonemes have cues visible on lips. Labial consonants by deaf are more intelligible than lingual consonants. Speech-training systems based on visual feedback of vocal tract shape are useful for improvement in vowel articulation. ♠♠ ►► 1. Intro. 2. Visual STA 9 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction (4/6) Estimation of Vocal Tract (VT) Shape Direct methods ▫ X-ray imaging, ▫ MRI ▫ Optopalatography (EPG) ▫ Electromagnetic articulography (EMA) ▫ Ultrasonic imaging Indirect techniques ♦ Acoustic measurement at lips ▫ Impedance ▫ Impulse response ♦ Processing of speech signal ▫ Linear Predictive Coding (LPC) ▫ Formant analysis ▫ Articulatory analysis by synthesis ♠♠ ►► 1. Intro. 2. Visual STA 10 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction (5/6) LPC Based Estimation of VT Shape ▪ Automated tracking of formants not required. ▪ Real-time processing feasible. ▪ Transformation of LPC coefficients into other parameter sets for interpolation and smoothening of estimated shapes. ▪ Estimation satisfactory for vowels. ▪ Failure of shape estimation during stop closure due to very low signal energy & unavailability of relevant spectral information. ▪ Indication of place of constriction during consonants critical for a speech training aid. ♠♠ ►► 1. Intro. 2. Visual STA 11 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction (6/6) Research Objectives • To develop techniques for estimation of place of constriction during oral stop closures of vowelconsonant-vowel syllables, for use in the speech training aids. • To improve consistency of the estimated VT shapes • To develop speech training aids with visual feedback of the VT shape and articulatory efforts ♠♠ ►► 1. Intro. 2. Visual STA 12 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 13 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 2. Visual Speech-training Aids (1/3) Speech-training ♦ Feedback of Acoustic Parameters ▫ speech intensity ▫ fundamental freq. ▫ spectral features ♦ Feedback of Articulatory Parameters ▫ voicing ▫ nasality ▫ lip & vocal tract movement ♦ Simultaneous display of the desired & estimated patterns for minimizing the mismatch. ♠♠ ►► 1. Intro. 2. Visual STA 14 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 2. Visual Speech-training Aids (2/ 3) Earlier Studies ▪ Coyne (1938) Gruenz & Schott (1949): Feedback of pitch ▪ Risberg (1968): Visual feedback of acoustic / articulatory parameters [indicators for frication, intonation, rhythm, nasalization, spectrum] ▪ Flecher (1982): PC based system called Dynamic Orometer [feedback of movement of tongue, pattern of tongue contact against teeth & roof of mouth, movement of lips & jaw, spectrum, F 0, intensity] ▪ Bernstein et. al. (1986): PC based system for sustained voicing & intensity control 1. Intro. 2. Visual STA 3. LPC VTSE 4. VTSE PC Impro, VTS vowel articulation ▪ Zahorian & Venkat (1990): DSC 5. based 6. Visual Disp. 7. Con. ♦♦ ◄◄ ♠♠ ►► 15 / 95

P. C. Pandey, EE Dept, IIT Bombay 2. Visual Speech-training Aids (3/3) Systems for Vocal Tract Shape Visualization ▪ LPC / formants based speech analysis [e. g. , Wakita (1973), Ladefoged et al. (1978), Yu & Ching (1996), Kshirsagar (1998), Mahdi (2003), Deng et al. (2005)] ▪ Type of displays, games, motivation, etc for speech training [e. g. , Crichton & Fallside (1974), Pardo (1982), Bernstein et al. (1986), Aguilera et al. (1986), Shigenaga & Kubo (1986), Javkin et al. (1993), Park et al. (1994), Oliveira & Souza (1997), Watanabe et al. (2000)] ▪ Commercially available PC based training systems Real time estimation & display of vocal tract shape [e. g. , Language Vision Inc. (2003)] Games, motivation, etc. [Dr. Speech Software Group (2003), Video Voice Speech Training System (2003)] ♠♠ ►► 1. Intro. 2. Visual STA 16 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 17 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 3. LPC Based Vocal Tract Shape Estimation (1/16) 3. 1 Introduction ▪ VT shape estimation based on LPC analysis & Wakita’s model (Wakita, 1973) ▪ Speech processing and display package ‘VTAG-1’ developed in Matlab ▪ Analysis for shape estimation using Areagram, 2 D display of square-root of VT area with time & distance (from glottis towards lips) ▪ Selection of optimum parameter values analysis window size, LPC order, sampling rate ▪ Application: vowels & VCV utterances ♠♠ ►► 1. Intro. 2. Visual STA 18 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

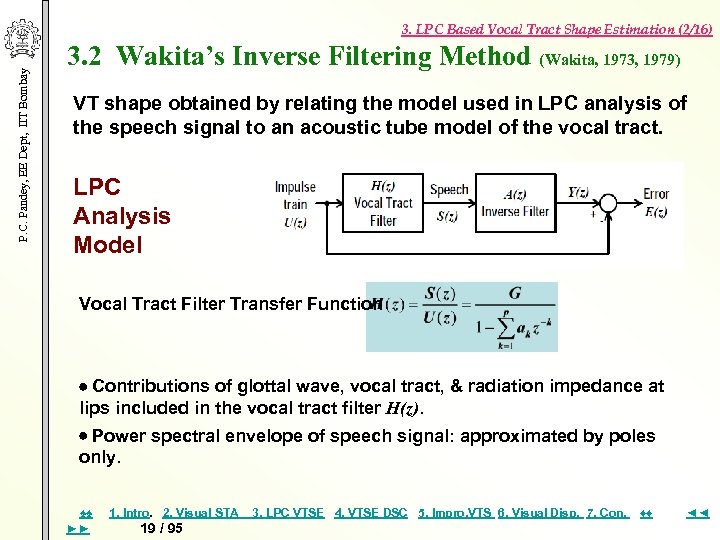
P. C. Pandey, EE Dept, IIT Bombay 3. LPC Based Vocal Tract Shape Estimation (2/16) 3. 2 Wakita’s Inverse Filtering Method (Wakita, 1973, 1979) VT shape obtained by relating the model used in LPC analysis of the speech signal to an acoustic tube model of the vocal tract. LPC Analysis Model Vocal Tract Filter Transfer Function Contributions of glottal wave, vocal tract, & radiation impedance at lips included in the vocal tract filter H(z). Power spectral envelope of speech signal: approximated by poles only. ♠♠ ►► 1. Intro. 2. Visual STA 19 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 3. LPC Based Vocal Tract Shape Estimation (3/16) Inverse Filter = predictor coefficients = prediction order For min. mean squared error, αk ≈ ak & A(z) is the inverse vocal tract filter A +6 db/octave pre-emphasis used to compensate for the spectral tilt due to source and radiation characteristics. Predictor coefficients obtained for short segments of speech as the vocal tract is time varying ♠♠ ►► 1. Intro. 2. Visual STA 20 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

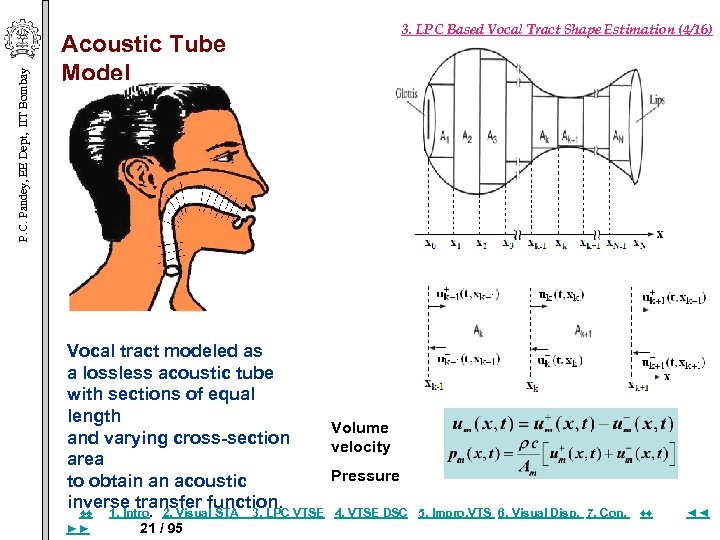
P. C. Pandey, EE Dept, IIT Bombay Acoustic Tube Model 3. LPC Based Vocal Tract Shape Estimation (4/16) Vocal tract modeled as a lossless acoustic tube with sections of equal length Volume and varying cross-section velocity area Pressure to obtain an acoustic inverse transfer function. VTSE 4. VTSE DSC ♠♠ 1. Intro. 2. Visual STA 3. LPC ►► 21 / 95 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay Acoustic Tube Model (contd. ) 3. LPC Based Vocal Tract Shape Estimation (5/16) Continuity of pressure variation between adjacent tubes Reflection of forward and backward waves Reflection coefficients depend on area of cross-section of two adjacent tubes and area ratios can be calculated from the reflection coefficients. Boundary conditions ▪ Lips modeled as radiation impedance ▪ Glottis modeled as acoustic impedance Losses not accounted Vibration of tube walls ▪ Viscous losses at the tube walls ▪ Thermal conduction at the walls ▪ ♠♠ ►► 1. Intro. 2. Visual STA 22 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay Computation of Area Values 3. LPC Based Vocal Tract Shape Estimation (6/16) LPC analysis Inverse filter transfer function A(z) from coefficients Km obtained by LPC analysis of speech signal segment Acoustic tube model Inverse filter transfer function D(z) from reflection coefficients μm at section interfaces Comparison of the two inverse filter transfer functions The reflection coefficients μm and hence area ratios can be obtained from LPC analysis of the speech signal. ♠♠ ►► 1. Intro. 2. Visual STA 23 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 3. LPC Based Vocal Tract Shape Estimation (7/16) Features of LPC Based VT Shape Estimation Usable for estimating fixed as well as transitional vocal tract configurations. Real-time processing feasible. Limitations of LPC Based VT Shape Estimation Improper estimation during nasalized vowels, nasal stops, and fricatives, due to deviations from all-pole filter model. Error in estimation due to band-limited speech signal. Error due to uncertain glottal source characteristics. Error during varying tract configuration due to assumption of fixed area at the glottal end. Variability in vocal tract shape during fixed tract configuration due to variations in the position of the analysis window with respect to the glottal pulse. Improper 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. low signal ◄◄ ♠♠ 1. Intro. estimation during stop closures due to very 7. Con. ♦♦ ►► energy. 24 / 95

P. C. Pandey, EE Dept, IIT Bombay 3. LPC Based Vocal Tract Shape Estimation (8/16) 3. 3 Implementation of LPC Based VT Estimation Fs = 11. 025 k. Hz LPC order = 12 Analysis frame duration: 2 (avg. pitch period) Analysis window: Hamming Window shift: 5 ms Pre-emphasis for 6 d. B/octave equalization Reflection coefficients obtained from LPC autocorrelation coefficients using Robinson's Method. Area ratios obtained from reflection coefficients. Area values obtained by multiplying the area ratios by an assumed area at the glottis end. ♠♠ ►► 1. Intro. 2. Visual STA 25 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 3. LPC based Vocal Tract Shape Estimation (9/16) 3. 4 Application: Vowels & VCV Utterances ▪ Natural & synthesized vowels analyzed for shape estimation for checking consistency studying effect of pitch and amplitude variation ▪ VCV syllables involving semivowels (representing low energy, non-continuant, voiced sounds) for checking shape tracking during VC & CV transitions ▪ VCV syllables involving stop consonants for shape estimation during transition and closure segments ▪ Use of VCV syllables for speech training short duration of dynamic shape display easier for a hearing impaired child to monitor & mimic ♠♠ ►► 1. Intro. 2. Visual STA 26 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

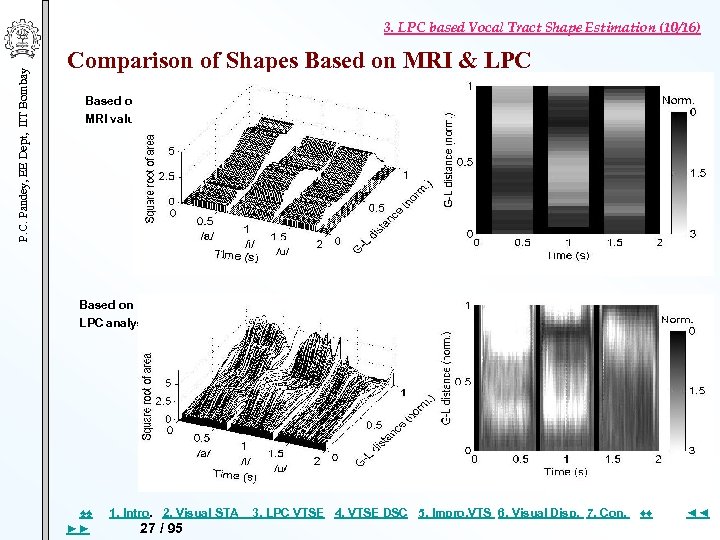
P. C. Pandey, EE Dept, IIT Bombay 3. LPC based Vocal Tract Shape Estimation (10/16) Comparison of Shapes Based on MRI & LPC Based on MRI values Based on LPC analysis ♠♠ ►► 1. Intro. 2. Visual STA 27 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

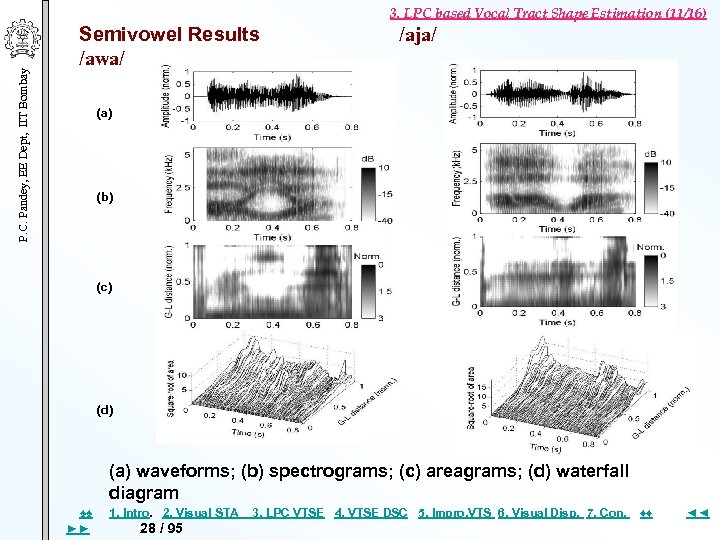
P. C. Pandey, EE Dept, IIT Bombay 3. LPC based Vocal Tract Shape Estimation (11/16) Semivowel Results /awa/ /aja/ (a) (b) (c) (d) (a) waveforms; (b) spectrograms; (c) areagrams; (d) waterfall diagram ♠♠ ►► 1. Intro. 2. Visual STA 28 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

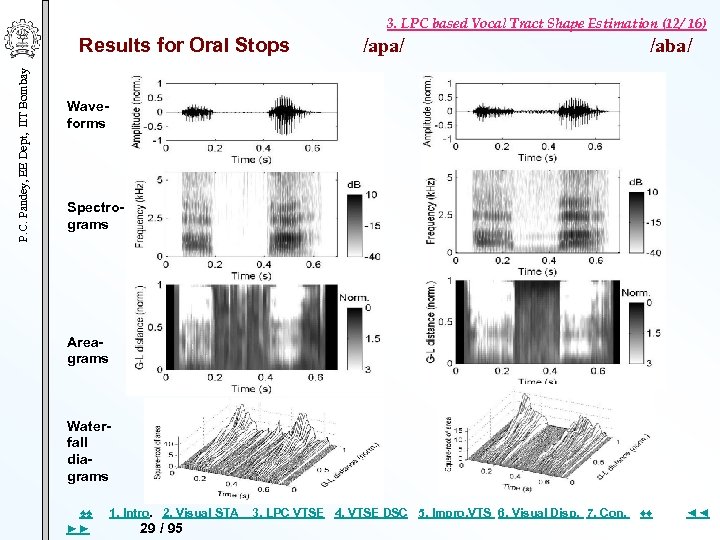
3. LPC based Vocal Tract Shape Estimation (12/ 16) P. C. Pandey, EE Dept, IIT Bombay Results for Oral Stops /apa/ /aba/ Waveforms Spectrograms Areagrams Waterfall diagrams ♠♠ ►► 1. Intro. 2. Visual STA 29 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

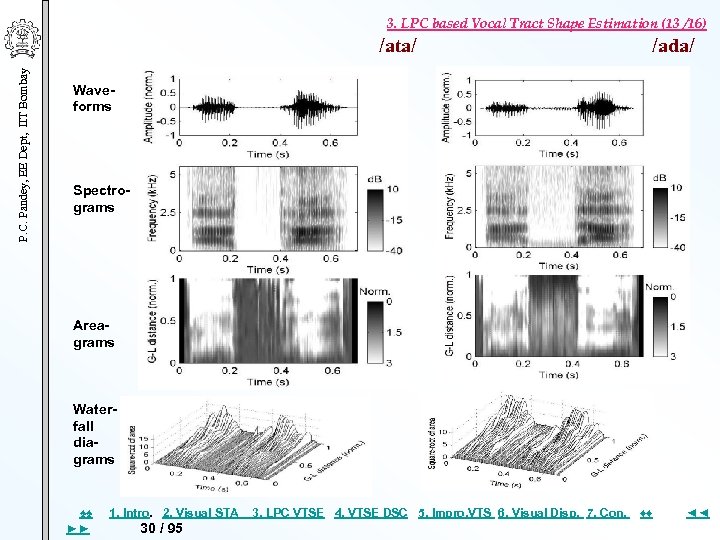
3. LPC based Vocal Tract Shape Estimation (13 /16) P. C. Pandey, EE Dept, IIT Bombay /ata/ /ada/ Waveforms Spectrograms Areagrams Waterfall diagrams ♠♠ ►► 1. Intro. 2. Visual STA 30 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

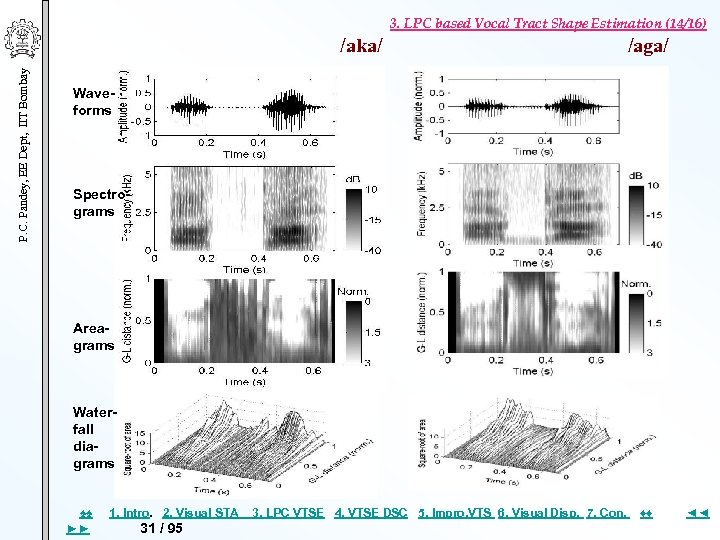
3. LPC based Vocal Tract Shape Estimation (14/16) P. C. Pandey, EE Dept, IIT Bombay /aka/ /aga/ Waveforms Spectrograms Areagrams Waterfall diagrams ♠♠ ►► 1. Intro. 2. Visual STA 31 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

3. LPC based Vocal Tract Shape Estimation (15/16) P. C. Pandey, EE Dept, IIT Bombay Result Summary of LPC Based VT Estimation Vowels Proper tongue elevation & match of the shapes with the MRI data, but a significant frame-to-frame variation Estimated shapes not significantly affected by ▪ step/ramp pitch variation ▪ signal amplitude variation of 40 d. B Semivowels Place of constriction properly reflected in areagrams Oral stops Inconsistent VT shape during stop closures VT shapes during VC and CV transitions ▪ distinctly different for different places of closures. ▪ related to movement of articulators during VC & CV transitions and may contain information about the place of closure. ♠♠ ►► 1. Intro. 2. Visual STA 32 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 3. LPC based Vocal Tract Shape Estimation (16/16) 3. 5 Further Investigations Use of bivariate surfaces, representing values related to vocal tract shape (area values, or some transformed representation ) over the VC & CV transition segments, for estimating the place of closure. ♠♠ ►► 1. Intro. 2. Visual STA 33 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 34 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (1/38) 4. 1 Proposed Technique Production of VCV syllables with oral stop consonants : movement of articulators from the articulatory position of the vowel towards to that of the stop closure to that of the vowel. ♦ Dynamic variation in vocal tract shape and formants during VC and CV transitions related to movement of articulators. Surface modeling of the time varying vocal tract shape during the transitions preceding and following the stop closure for estimating the place of constriction, during the closure duration. Surface modeling of time varying vocal tract shape using 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ♠♠ 1. Intro. ♦ ►► 35 / 95 ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (2/38) Investigations Modeling of articulatory dynamics during CV and VC transitions: bivariate surface modeling of area values during VC & CV transitions by (i) leastsquares second & third degree bivariate polynomials & (ii) Delaunay triangulation based surfaces. Estimation of vocal tract shape or place of constriction during the stop closure: interpolation of the area value using the bivariate surface model. Exploring the use of LSFs (obtained from LPC coefficients) for modeling and interpolation ♠♠ ►► 1. Intro. 2. Visual STA 36 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (3/38) Modeling of vocal tract shape as a function of time Bivariate surface modeling of the data consisting of area values & LSFs, as a function of distance (G-L) and time, by ▪ 2 nd and 3 rd degree bivariate polynomials ▪ Surface modeling by Delaunay triangulation ♠♠ ►► 1. Intro. 2. Visual STA 37 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (4/38 Least-squares polynomial approximation ▪ Find f(x) that matches q data points gn within a small error rn i. e. , ▪ In general, such that minimized is where ck: set of p parameters to be determined & Φk: set of a priori known functions ▪ In matrix notation, where, ▪ To reduce interpolation errors: usually p < q ▪ Least-squares solution by pseudo-inverse of A ♠♠ ►► 1. Intro. 2. Visual STA 38 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

4. Estimation During Stop Closures (5/38) P. C. Pandey, EE Dept, IIT Bombay Bivariate Polynomials 2 nd degree 3 rd degree where f(x, y) models g(x, y) within a small error r(x, y), and c 0 -c 5 & d 0 -d 9 to be chosen to approximate {g(x, y)} in the least-squares sense. Area values and LSFs (represented by g(x, y)) during VC & CV transition regions approximated by second and third degree bivariate polynomial surfaces. ♠♠ ►► 1. Intro. 2. Visual STA 39 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (6/38) Selection of Area Values (or LSFs) for Surface Approximation and where Lcol = xb xa + 1 Rcol = xd xc + 1 Overdetermined system of simultaneous linear eqns. for q > 6 for second degree & q >10 for third degree polynomial. Least-squares solution → approximated second or third degree surfaces. ♠♠ ►► 1. Intro. 2. Visual STA 40 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (7/38) Simultaneous Linear Equations in Matrix Notation Az = b+r For 2 nd degree polynomial approximation, ♠♠ ►► 1. Intro. 2. Visual STA 41 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

4. Estimation During Stop Closures (8/38) P. C. Pandey, EE Dept, IIT Bombay For 3 rd degree polynomial approximation, ♠♠ ►► 1. Intro. 2. Visual STA 42 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During stop Closures (9/38) Least-squares solution for simultaneous linear equations by pseudo- inverse operation gives 2 D interpolation of polynomial surfaces during stop closures for carried out using where for 2 nd degree polynomial ♠♠ ►► 1. Intro. 2. Visual STA 43 / 95 for 3 rd degree 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (10/38) Delaunay Triangulation Based Surface Modeling ▪ Triangulation involves subdivision of an area (volume) into triangles (tetrahedrons) ▪ Delaunay triangulation & its properties A set of lines connecting each point to its natural neighbor No data points are contained within a circle circumscribing the triangles Maximizes the smallest angle over all triangulation ▪ Delaunay surface modeling of area values & LSFs during VC & CV transition regions carried out (using Matlab® functions) ▪ For estimation of vocal tract shape and/or place of constriction 2 D Delaunay surface interpolation during stop closure carried ♠♠ out 1. Intro. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄ ►► 44 / 95

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (11/38) Estimation of Stop Closure Boundary Locations ▪ Estimation step 1: estimation of VCV utterance end-points step 2: based on step 1, stop closure boundary locations estimated (using avg. short time magnitude & empirically selected thresholds) ▪ Estimated stop closure end location shifted beyond the fricative burst at closure release (LPC based area estimation during frication becomes generally inconsistent & uncorrelated to place of articulation) ♠♠ ►► 1. Intro. 2. Visual STA 45 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (12/38) 4. 2 Validation Method Segments with static vocal tract shape: vowels /a/, /i/, & /u/ Segments with transitional vocal tract shape: /aja/ & /awa/ Vowels, /aja/ & /awa/ with artificially silenced medial segment for proper recovery of vocal tract shape and/or place of articulation during silence gap. ▪ Analysis of VCV syllables for estimation of ● minimum transition segments required ● typical surface generation & interpolation parameters required (no. of frames to the left Lcol & right Rcol of silence gap and no. of rows j) for proper recovery of vocal tract shape and/or place of ♠♠ 1. Intro. 2. Visual articulation. STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ►► 46 / 95 ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (13/38) 4. 3 Results: Estimation of Static VT Shapes ● Vowels : (i) synthesized (ii) recorded from a male speaker. ● Medial silence segments of different duration artificially introduced. ♠♠ ►► 1. Intro. 2. Visual STA 47 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

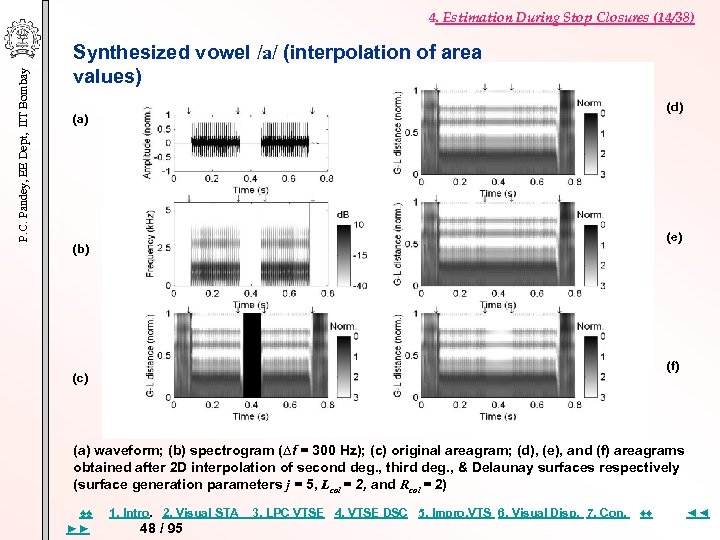
P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (14/38) Synthesized vowel /a/ (interpolation of area values) (d) (a) (e) (b) (f) (c) (a) waveform; (b) spectrogram (∆f = 300 Hz); (c) original areagram; (d), (e), and (f) areagrams obtained after 2 D interpolation of second deg. , third deg. , & Delaunay surfaces respectively (surface generation parameters j = 5, Lcol = 2, and Rcol = 2) ♠♠ ►► 1. Intro. 2. Visual STA 48 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (15/38) 4. 4 Results: Estimation of Transitional VT Shapes VCV utterances recorded from three male (SM 1, SM 2, & SM 3) & two female (SF 4 & SF 5) speakers. ♠♠ ►► 1. Intro. 2. Visual STA 49 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

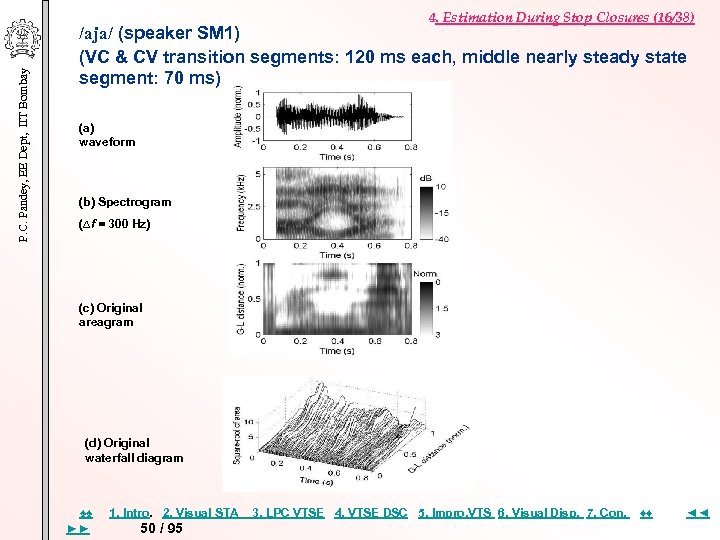
P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (16/38) /aja/ (speaker SM 1) (VC & CV transition segments: 120 ms each, middle nearly steady state segment: 70 ms) (a) waveform (b) Spectrogram (∆f = 300 Hz) (c) Original areagram (d) Original waterfall diagram ♠♠ ►► 1. Intro. 2. Visual STA 50 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

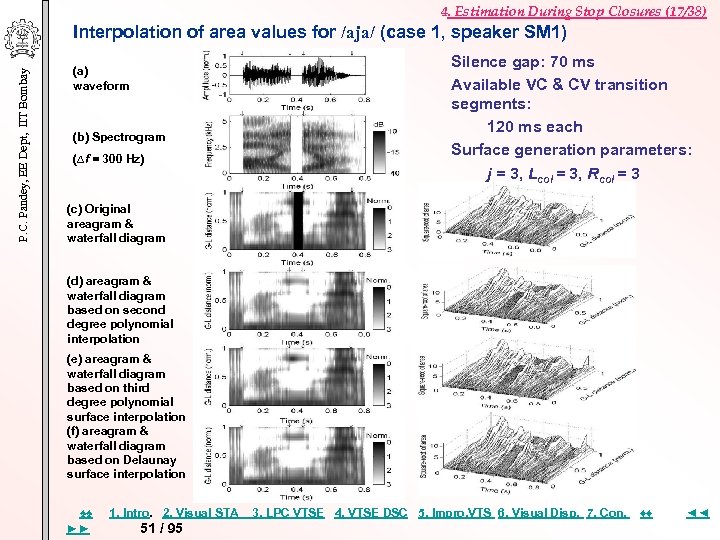
4. Estimation During Stop Closures (17/38) P. C. Pandey, EE Dept, IIT Bombay Interpolation of area values for /aja/ (case 1, speaker SM 1) (a) waveform (b) Spectrogram (∆f = 300 Hz) Silence gap: 70 ms Available VC & CV transition segments: 120 ms each Surface generation parameters: j = 3, Lcol = 3, Rcol = 3 (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 51 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

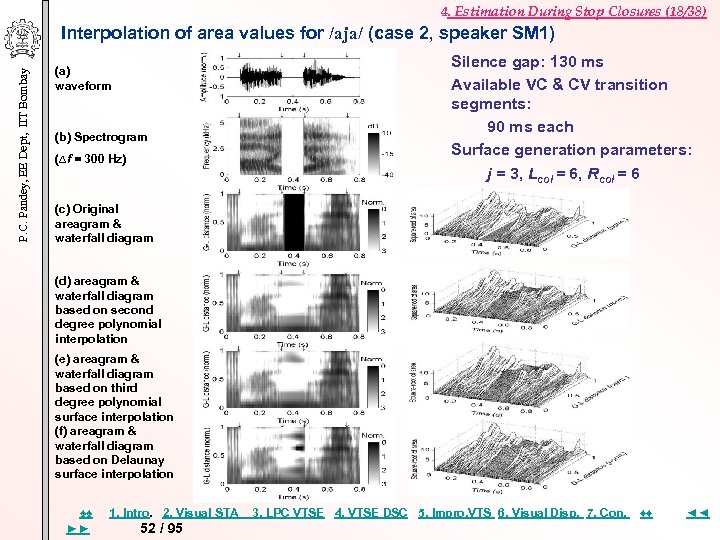
4. Estimation During Stop Closures (18/38) P. C. Pandey, EE Dept, IIT Bombay Interpolation of area values for /aja/ (case 2, speaker SM 1) (a) waveform (b) Spectrogram (∆f = 300 Hz) Silence gap: 130 ms Available VC & CV transition segments: 90 ms each Surface generation parameters: j = 3, Lcol = 6, Rcol = 6 (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 52 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

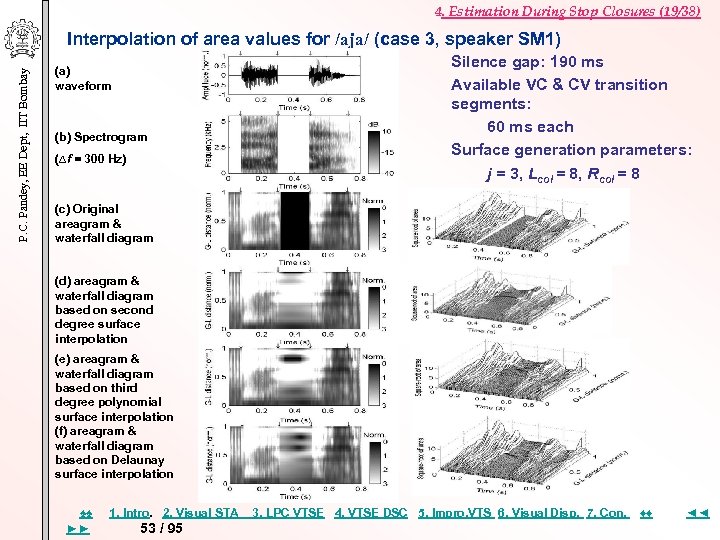
4. Estimation During Stop Closures (19/38) P. C. Pandey, EE Dept, IIT Bombay Interpolation of area values for /aja/ (case 3, speaker SM 1) (a) waveform (b) Spectrogram (∆f = 300 Hz) Silence gap: 190 ms Available VC & CV transition segments: 60 ms each Surface generation parameters: j = 3, Lcol = 8, Rcol = 8 (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 53 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

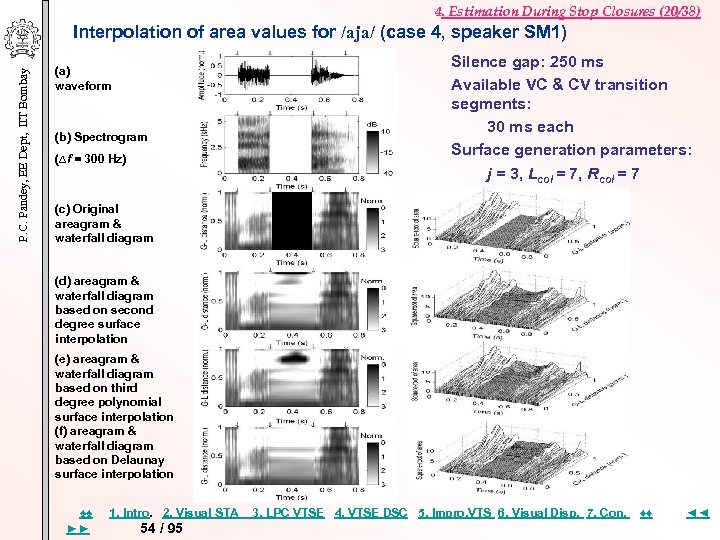
4. Estimation During Stop Closures (20/38) P. C. Pandey, EE Dept, IIT Bombay Interpolation of area values for /aja/ (case 4, speaker SM 1) (a) waveform (b) Spectrogram (∆f = 300 Hz) Silence gap: 250 ms Available VC & CV transition segments: 30 ms each Surface generation parameters: j = 3, Lcol = 7, Rcol = 7 (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 54 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (21/38) Observations ▪ Second & third degree polynomial surface interpolation of area values result in proper estimation of vocal tract shape for the first two cases (transition seg. = 120, 90 ms) place of constriction for all the four cases (tr. seg. = 120, 90, 60, 30 ms) ▪ Delaunay triangulation based surface interpolation of area values proper estimation of place of constriction for the first two cases ▪ Minimum 30 ms of VC & CV transition segments required for proper estimation of place of articulation. ♠♠ 1. Intro. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄ ►► 55 / 95

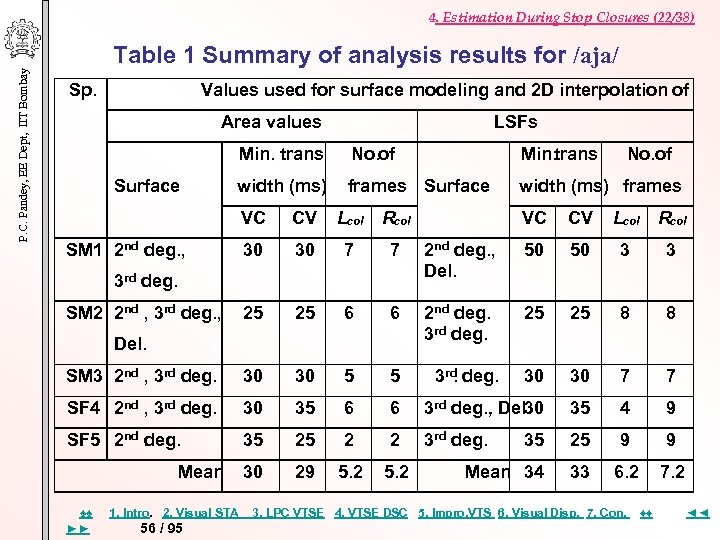
P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (22/38) Table 1 Summary of analysis results for /aja/ Sp. Values used for surface modeling and 2 D interpolation of Area values LSFs Min. trans Surface No. of Min. trans width (ms) frames Surface width (ms) frames VC CV Lcol Rcol 30 30 7 7 25 25 6 SM 3 2 nd , 3 rd deg. 30 30 SF 4 2 nd , 3 rd deg. . 30 SF 5 2 nd. deg. SM 1 2 nd deg. , VC CV Lcol Rcol 2 nd deg. , Del. 50 50 3 3 6 2 nd deg. , . 3 rd deg. 25 25 8 8 5 5 3 rd deg. . 30 30 7 7 35 6 6 3 rd deg. , Del 30. 35 4 9 35 25 2 2 3 rd deg. . 35 25 9 9 30 29 5. 2 Mean 34 33 6. 2 7. 2 3 rd deg. SM 2 2 nd , 3 rd deg. , Del. Mean ♠♠ ►► 1. Intro. 2. Visual STA 56 / 95 No. of 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

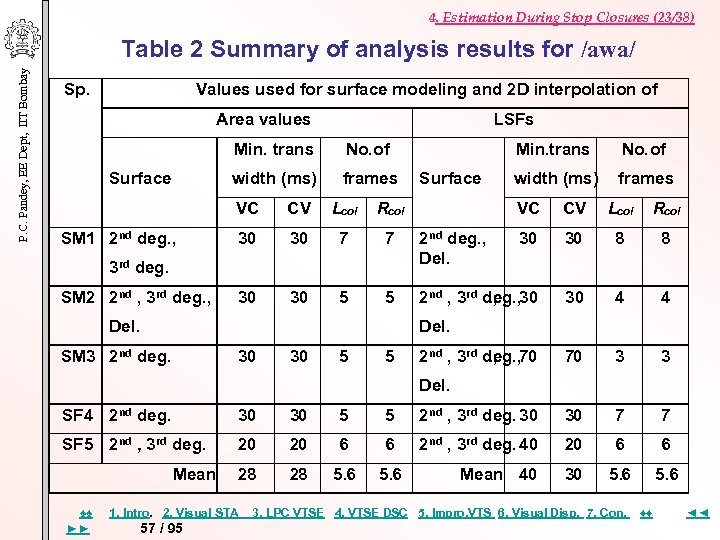
4. Estimation During Stop Closures (23/38) P. C. Pandey, EE Dept, IIT Bombay Table 2 Summary of analysis results for /awa/ Sp. Values used for surface modeling and 2 D interpolation of Area values LSFs Min. trans width (ms) Surface No. of frames Min. trans Surface VC SM 1 2 nd deg. , CV Lcol Rcol 30 30 7 7 2 nd deg. , Del. 30 30 5 5 3 rd deg. SM 2 2 nd , 3 rd deg. , Del. No. of width (ms) frames VC CV Lcol Rcol 30 30 8 8 2 nd , 3 rd deg. , 30. , 30 4 4 70 3 3 Del. SM 3 2 nd deg. 30 30 5 5 2 nd , 3 rd deg. , 70. , Del. SF 4 2 nd deg. 30 30 5 5 2 nd , 3 rd deg. 30 30 7 7 SF 5 2 nd , 3 rd deg. . 20 20 6 6 2 nd , 3 rd deg. 40. 20 6 6 28 28 5. 6 Mean 40 30 5. 6 Mean ♠♠ ►► 1. Intro. 2. Visual STA 57 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (24/38) Observations ▪ Proper estimation of place of articulation dependent on type of surface used for modeling of VC & CV transition values number of frames used during VC & CV transition segments ▪ Minimum required transition width in a syllable is more in case of surface modeling of LSFs compared to surface modeling of area values. ▪ 2 D interpolation based on second degree polynomial surface approximation of area values & LSFs found to be the most successful technique ♠♠ ►► 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. of required minimum mean VC & CV transition segments ♦♦ 1. Intro. 2. Visual STA 58 / 95 ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (25/38) 4. 5 Results: Estimation during Stop Closures ▪ Bivariate surface modeling and interpolation (i) Second degree polynomial (quadratic) approximation (ii) Third degree polynomial (cubic) approximation (iii) Delaunay surfaces ▪ Parameters used for modeling and interpolation (i) Area values, (ii) LSFs ▪ Estimation of place of closure in VCV syllables Stop consonants: /p/, /b/, /t/, /d/, /k/, & /g/ Utterances /a. Ca/, /i. Ca/ (3 M, 2 F speakers) /a. Ci/, /i. Ci/, & /u. Cu/ (1 M speaker) ♠♠ ►► 1. Intro. 2. Visual STA 59 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

4. Estimation During Stop Closures (26/38) P. C. Pandey, EE Dept, IIT Bombay ▪ Verification of estimated place of constriction : comparison with earlier reported articulation places based on MRI & X-ray images Typical places of constriction (normalized distance of 0 to 1, 0: glottis, 1: lips) Bilabial stops (p, b) : 1 Alveolar stops (t, d) : 0. 75 to 0. 89 Velar stops (k, g) : 0. 47 to 0. 7 ♠♠ ►► 1. Intro. 2. Visual STA 60 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

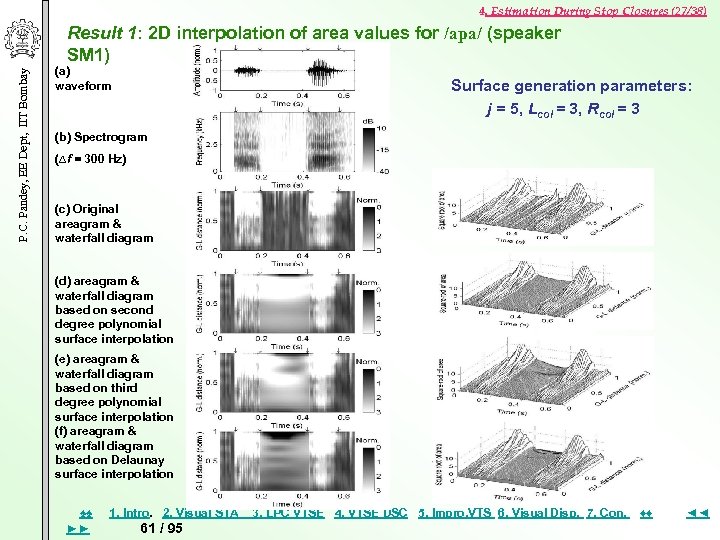
4. Estimation During Stop Closures (27/38) P. C. Pandey, EE Dept, IIT Bombay Result 1: 2 D interpolation of area values for /apa/ (speaker SM 1) (a) waveform Surface generation parameters: j = 5, Lcol = 3, Rcol = 3 (b) Spectrogram (∆f = 300 Hz) (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 61 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

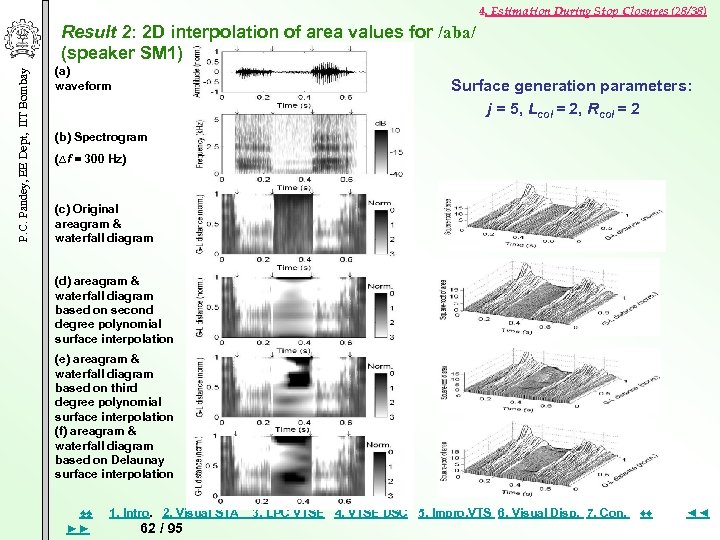
4. Estimation During Stop Closures (28/38) P. C. Pandey, EE Dept, IIT Bombay Result 2: 2 D interpolation of area values for /aba/ (speaker SM 1) (a) waveform Surface generation parameters: j = 5, Lcol = 2, Rcol = 2 (b) Spectrogram (∆f = 300 Hz) (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 62 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

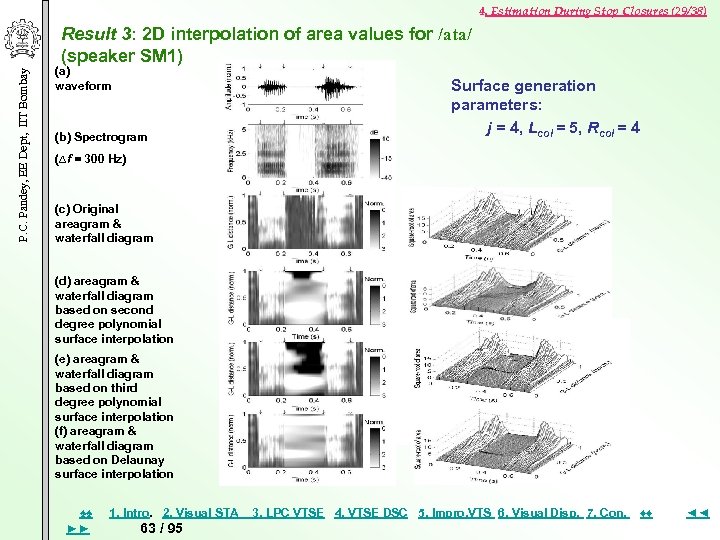
4. Estimation During Stop Closures (29/38) P. C. Pandey, EE Dept, IIT Bombay Result 3: 2 D interpolation of area values for /ata/ (speaker SM 1) (a) waveform (b) Spectrogram Surface generation parameters: j = 4, Lcol = 5, Rcol = 4 (∆f = 300 Hz) (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 63 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

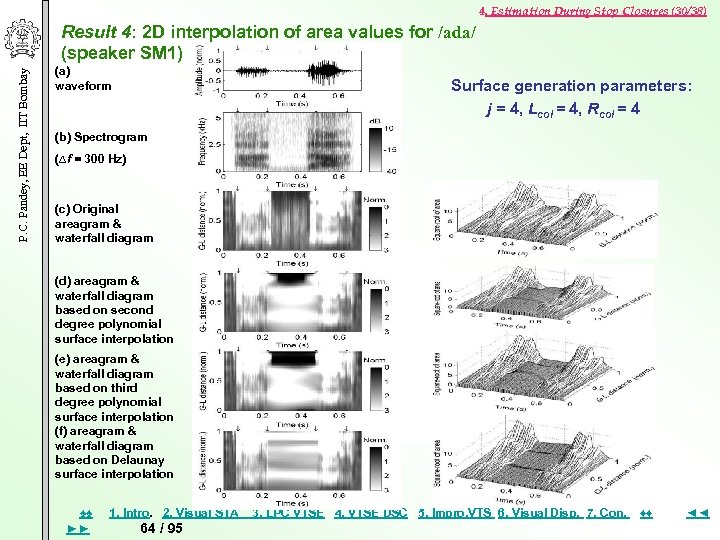
4. Estimation During Stop Closures (30/38) P. C. Pandey, EE Dept, IIT Bombay Result 4: 2 D interpolation of area values for /ada/ (speaker SM 1) (a) waveform Surface generation parameters: j = 4, Lcol = 4, Rcol = 4 (b) Spectrogram (∆f = 300 Hz) (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 64 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

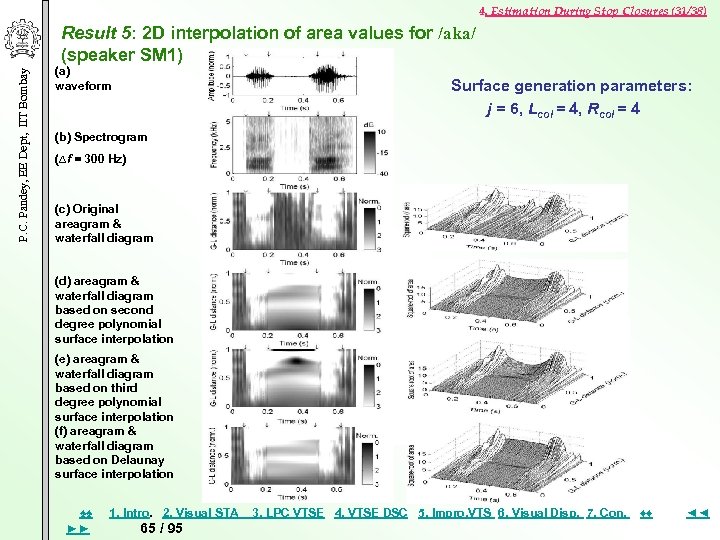
4. Estimation During Stop Closures (31/38) P. C. Pandey, EE Dept, IIT Bombay Result 5: 2 D interpolation of area values for /aka/ (speaker SM 1) (a) waveform Surface generation parameters: j = 6, Lcol = 4, Rcol = 4 (b) Spectrogram (∆f = 300 Hz) (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 65 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

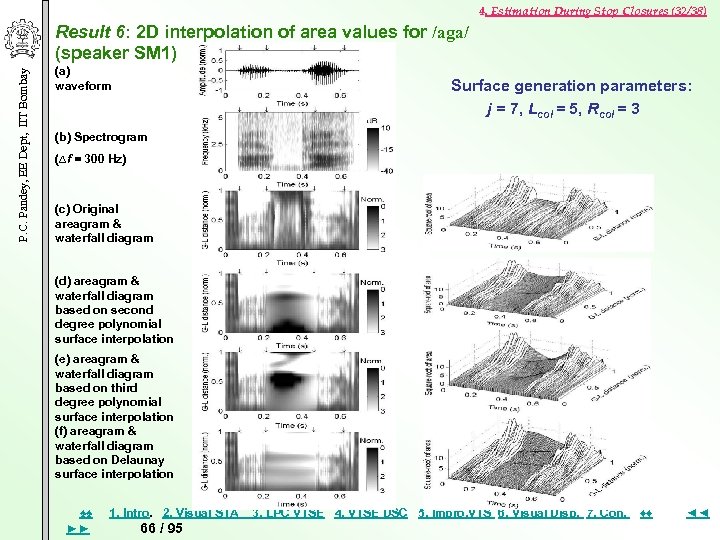
4. Estimation During Stop Closures (32/38) P. C. Pandey, EE Dept, IIT Bombay Result 6: 2 D interpolation of area values for /aga/ (speaker SM 1) (a) waveform Surface generation parameters: j = 7, Lcol = 5, Rcol = 3 (b) Spectrogram (∆f = 300 Hz) (c) Original areagram & waterfall diagram (d) areagram & waterfall diagram based on second degree polynomial surface interpolation (e) areagram & waterfall diagram based on third degree polynomial surface interpolation (f) areagram & waterfall diagram based on Delaunay surface interpolation ♠♠ ►► 1. Intro. 2. Visual STA 66 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

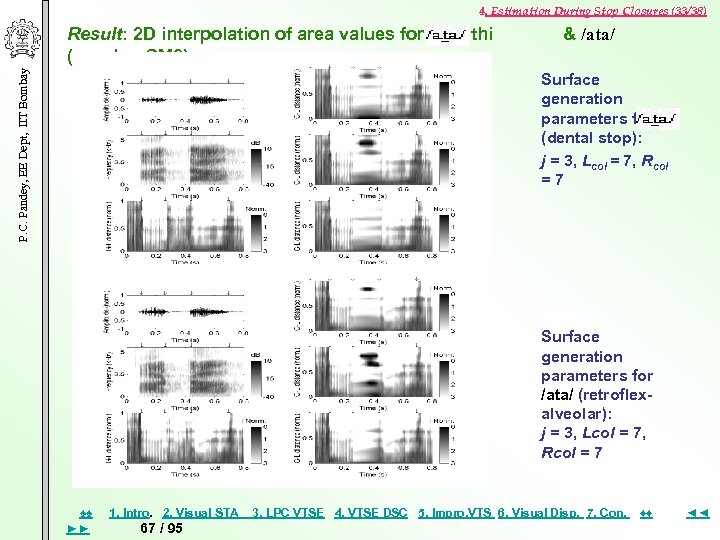
4. Estimation During Stop Closures (33/38) P. C. Pandey, EE Dept, IIT Bombay Result: 2 D interpolation of area values for Marathi (speaker SM 2) & /ata/ Surface generation parameters for (dental stop): j = 3, Lcol = 7, Rcol =7 Surface generation parameters for /ata/ (retroflexalveolar): j = 3, Lcol = 7, Rcol = 7 ♠♠ ►► 1. Intro. 2. Visual STA 67 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

4. Estimation During Stop Closures (34/38) P. C. Pandey, EE Dept, IIT Bombay Result Summary ▪ For /a. Ca/, estimation of place of constriction for bilabial, alveolar, & velar stops is most accurate with 2 nd degree polynomial surface modeling of area values & LSFs (in conformity with observations during initial validation of the technique with artificially introduced silence gaps in semivowels) → articulatory movement during production of /a. Ca/ modeled more appropriately by 2 nd degree polynomials. ▪ For /i. Ca/, /a. Ci/, & /i. Ci/, estimation of place of constriction for velar stops is not consistent across speakers → the proposed technique less effective 7. Con. ♦♦ ◄◄ for 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 68 / 95 articulatory movement involving transition of place of ♠♠ ►► 1. Intro. 2. Visual STA

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (35/38) ▪ For /a. Ca/ involving bilabial, alveolar, & velar stops, average number of frames required for proper surface modeling based on area values (6. 1, 6. 8, and 5. 9 frames resp. ) are less compared to modeling of LSFs (7. 6, 7. 5, and 7. 3 frames resp. ) (in conformity with observations during initial validation of the technique with artificially introduced silence gaps in semivowels). ♠♠ ►► 1. Intro. 2. Visual STA 69 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (36/38) 4. 6 Direct Validation of the Technique Application of the technique on acoustic signals that have been simultaneously acquired with articulatory data ▪ Database from the University of Wisconsin. ▪ Articulatory data acquired using X-ray microbeam (XRMB) system. ▪ Articulatory plot shows position of pellets in the midsaggital plane. ▪ Position of pellets gives a point-parameterized representation of lingual, labial, and mandibular movements. ▪ Information about the lower part of the vocal tract not available. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♠♠ 1. Intro. ►► 70 / 95 ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 4. Estimation During Stop Closures (37/38) ▪ Sample articulatory plot ▪ 2 D interpolation based on second degree surfaces representing area values applied to 120 VCV syllables of the type /^Ca/ (from XRMB database) involving stop consonants /b/, /d/, & /g/ for the estimation of place of closure. ▪ Estimated place of constriction compared with actual constriction locations obtained from articulatory database. ♠♠ ►► 1. Intro. 2. Visual STA 71 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

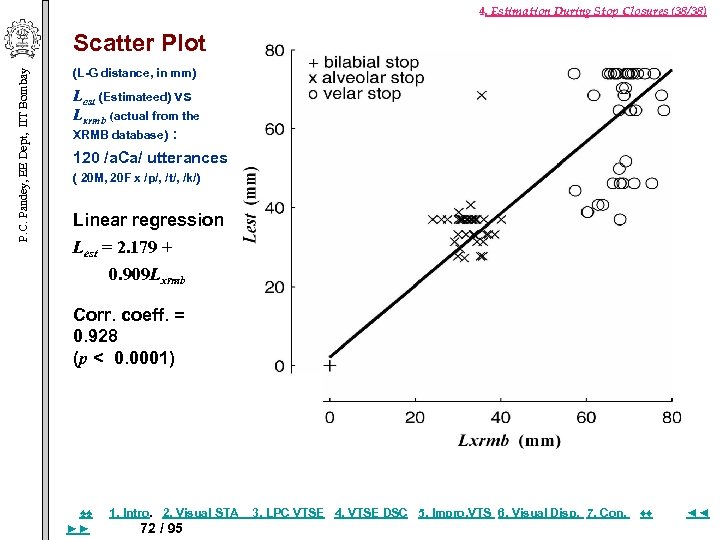
4. Estimation During Stop Closures (38/38) P. C. Pandey, EE Dept, IIT Bombay Scatter Plot (L-G distance, in mm) Lest (Estimateed) vs Lxrmb (actual from the XRMB database) : 120 /a. Ca/ utterances ( 20 M, 20 F x /p/, /t/, /k/) Linear regression Lest = 2. 179 + 0. 909 Lxrmb Corr. coeff. = 0. 928 (p < 0. 0001) ♠♠ ►► 1. Intro. 2. Visual STA 72 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 73 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 5. Improving the VT Shape Estimation (1/12) 5. 1 Objective of the Investigation Improving the consistency of the LPC-based estimation of the area values of the vocal tract cross-sections without smearing the variations during speech segments with transitional vocal tract configuration. ♠♠ ►► 1. Intro. 2. Visual STA 74 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 5. Improving the VT Shape Estimation (2/12) 5. 2 Variation in Vocal Tract Shape VT Shape Estimation by LPC Analysis ▪ Fs = 10 k. Hz, Pre-emphasis: 6 d. B/octave, LPC order = 12 ▪ Analysis frame length: twice the average pitch period ▪ Analysis window: Hamming Variation in the area values estimated with window shift of 5 ms, even for the vowel segments with fixed vocal tract configurations. Reduction in the variability possible by low-pass filtering (along time) of the estimated area values or by using a longer analysis window, but at the expense of smearing of the transitions during segments with transitional tract configurations e. g. diphthongs, VC and CV transitions. ♠♠ ►► 1. Intro. 2. Visual STA 75 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

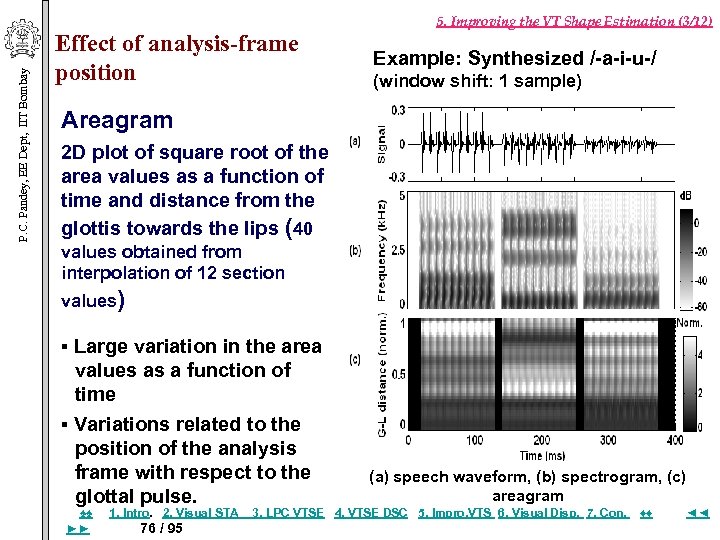
P. C. Pandey, EE Dept, IIT Bombay Effect of analysis-frame position 5. Improving the VT Shape Estimation (3/12) Example: Synthesized /-a-i-u-/ (window shift: 1 sample) Areagram 2 D plot of square root of the area values as a function of time and distance from the glottis towards the lips (40 values obtained from interpolation of 12 section values) ▪ Large variation in the area values as a function of time ▪ Variations related to the position of the analysis frame with respect to the glottal pulse. ♠♠ ►► 1. Intro. 2. Visual STA 76 / 95 (a) speech waveform, (b) spectrogram, (c) areagram 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay Earlier Studies 5. Improving the VT Shape Estimation (4/12) Rabiner et al. (1977) ▪ A substantial variation in the LPC prediction error with change in the position of the analysis frame. ▪ Variability in the prediction error could be reduced by all-pass filtering and pre-emphasis of the speech signal, but at the expense of an increase in the error. Mezzalama (1979) ▪ A large variation in the formants estimated by LPC analysis with change in the position of the analysis frame with respect to the glottal pulse. ▪ Variation could be reduced by selecting the frame length to be equal to the multiple of the pitch period and by repeatedly concatenating the frame before applying the analysis window. Mizoguchi et al. (1982): "Selective LP in time domain", involving rejection of speech segments corresponding to prediction error above a threshold, for reducing the variation in the prediction coefficients across the frames for steady-state vowel segments. Ma et al. (1993): Selection of speech samples on the basis of short-time energy found to be more robust for reducing the variation in the prediction coefficients than the selection based on LPC prediction error. ♠♠ ►► 1. Intro. 2. Visual STA 77 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

5. Improving the VT Shape Estimation (5/12) P. C. Pandey, EE Dept, IIT Bombay Selection of Frames for Reducing Variability in VT Shape Variation in the RMS value of the LPC prediction error with the analysis frame position. Frame positions corresponding to the minimum in the prediction error found to be related to the least estimation error in the vocal tract parameters. Difficulty in consistently locating the peaks or the valleys of the LPC prediction error. The variation in the prediction error found to be related to the GCIs, but the location of the frame positions for minimum error with respect to the GCIs found to be different for different vowels. Minima of the prediction error coincide with the minima of the windowed energy for steady-state vowel ♠♠ 1. Intro. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄ segments. ►► 78 / 95

P. C. Pandey, EE Dept, IIT Bombay 5. Improving the VT Shape Estimation (6/12) 5. 3 Method for Reducing Variability in Vocal Tract Shape Estimation Windowed Energy Index Automated selection of frames by using “windowed energy index”, calculated as the ratio of the energy of the windowed frame to the frame energy n Ew (n) = Windowed energy index for frame position w(m) = Hamming window of length N sn(m) = speech segment for the frame position n ♠♠ ►► 1. Intro. 2. Visual STA 79 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

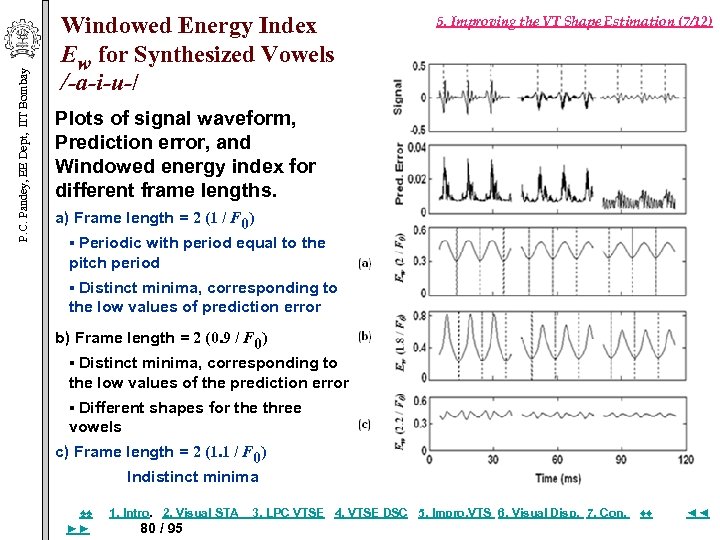
P. C. Pandey, EE Dept, IIT Bombay Windowed Energy Index Ew for Synthesized Vowels /-a-i-u-/ 5. Improving the VT Shape Estimation (7/12) Plots of signal waveform, Prediction error, and Windowed energy index for different frame lengths. a) Frame length = 2 (1 / F 0) ▪ Periodic with period equal to the pitch period ▪ Distinct minima, corresponding to the low values of prediction error b) Frame length = 2 (0. 9 / F 0) ▪ Distinct minima, corresponding to the low values of the prediction error ▪ Different shapes for the three vowels c) Frame length = 2 (1. 1 / F 0) Indistinct minima ♠♠ ►► 1. Intro. 2. Visual STA 80 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

5. Improving the VT Shape Estimation (8/12) P. C. Pandey, EE Dept, IIT Bombay Observations from Ew for Synthesized Vowels Variability in estimated area values can be reduced by selecting the frame positions corresponding to the minima in Ew , calculated with analysis frames of length equal to two pitch periods or slightly shorter. ♠♠ ►► 1. Intro. 2. Visual STA 81 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

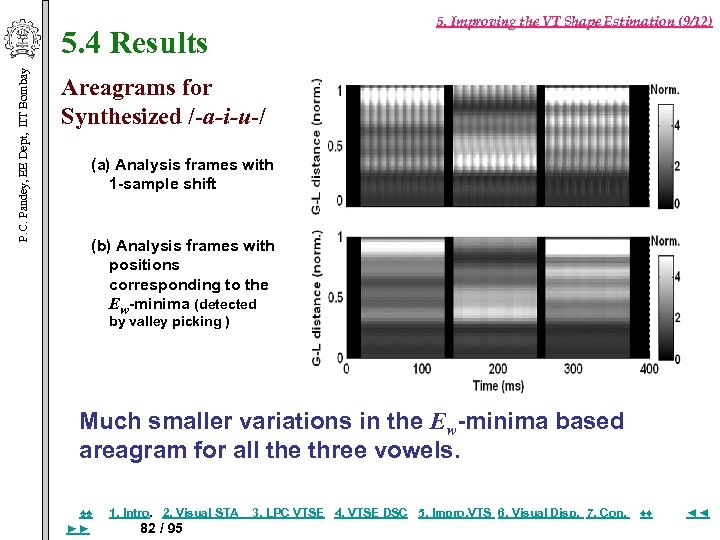
5. Improving the VT Shape Estimation (9/12) P. C. Pandey, EE Dept, IIT Bombay 5. 4 Results Areagrams for Synthesized /-a-i-u-/ (a) Analysis frames with 1 -sample shift (b) Analysis frames with positions corresponding to the Ew-minima (detected by valley picking ) Much smaller variations in the Ew-minima based areagram for all the three vowels. ♠♠ ►► 1. Intro. 2. Visual STA 82 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

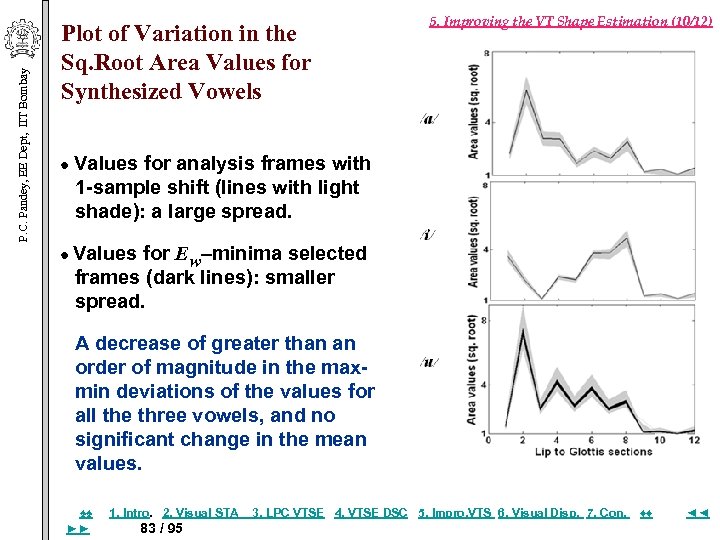
P. C. Pandey, EE Dept, IIT Bombay Plot of Variation in the Sq. Root Area Values for Synthesized Vowels 5. Improving the VT Shape Estimation (10/12) Values for analysis frames with 1 -sample shift (lines with light shade): a large spread. Values for Ew–minima selected frames (dark lines): smaller spread. A decrease of greater than an order of magnitude in the maxmin deviations of the values for all the three vowels, and no significant change in the mean values. ♠♠ ►► 1. Intro. 2. Visual STA 83 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

Example: Vowel-Semivowel-Vowel P. C. Pandey, EE Dept, IIT Bombay Synth. /aja/ 5. Improving the VT Shape Estimation (11/12) Natural /aja/ (speaker S 1) (a) speech waveform, (b) spectrogram, (c) 1 -sample shift areagram, (d) Ew–minima areagram Areagram with Ew–minima selected frames: Reduction in the variation during the fixed-tract configuration without smearing during the transitional configuration. ♠♠ ►► 1. Intro. 2. Visual STA 84 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 5. Improving the VT Shape Estimation (12/12) 5. 5 Result Summary Analysis frames positioned at Ew-minima resulted in ▪ low prediction error in LPC analysis, ▪ significantly reduced variability in the area values estimated by LP analysis during vowel segments with fixed-tract configurations. Consistency of vocal tract shape estimation improved without smearing the variations in the shape during semivowel segments with transitional-tract configuration. Method may be used to estimate the VC and CV transition area values during Vowel-Oral stop-Vowel utterances for improving ▪ the accuracy of the vocal tract shape during stop closures as estimated by bivariate surface modeling, ▪ vocal tract shape estimation for speech training aids. ♠♠ ►► 1. Intro. 2. Visual STA 85 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Dynamic Display of Vocal Tract Shape 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 86 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 6. Dynamic Display of Vocal Tract Shape(1/2) Speech Training System Display, with selectable frame rate ▪ Acoustic parameters ▫ pitch ▫ short-time energy ▫ voicing ▫ spectrogram ▪ Articulatory Efforts ▫ Vocal tract shape ▫ Movement of articulators (particularly the tongue & velum) Display of articulatory efforts & acoustic parameters for the uttered and the target utterances of short duration. Evaluation ♠♠ ►► 1. Intro. 2. Visual STA 87 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

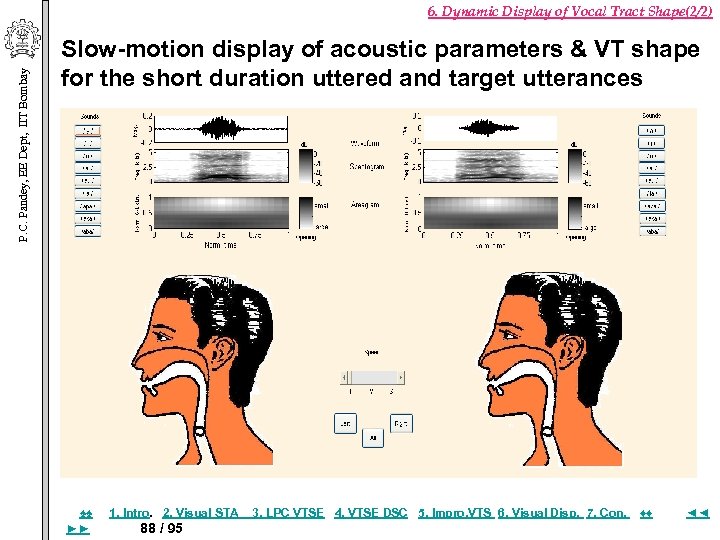
P. C. Pandey, EE Dept, IIT Bombay 6. Dynamic Display of Vocal Tract Shape(2/2) Slow-motion display of acoustic parameters & VT shape for the short duration uttered and target utterances ♠♠ ►► 1. Intro. 2. Visual STA 88 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 1. Introduction 2. Visual Speech-training Aids 3. LPC Based Vocal Tract Shape Estimation 4. Estimation of Vocal Tract Shape during Stop Closures 5. Improving the Consistency of Vocal Tract Shape Estimation 6. Visual Speech Training System 7. Summary & Conclusions ♠♠ ►► 1. Intro. 2. Visual STA 89 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 6. Summary & Conclusions (1/3) Summary of Investigations ▪ Implementation of VT shape estimation based on LPC analysis & Wakita’s model Selection of optimum values of analysis parameters for vowels. Study of the effect of pitch & amplitude variations on VT estimation. Study of VT estimation for VCV utterances with semivowels & oral stops. ▪ Estimation of place of closure in VCV utterances with oral stops Bivariate surface modeling of values related to vocal tract shape during VC & CV transition segments, based on leastsquares bivariate polynomials and Delaunay triangulation, and estimation of the shape by interpolation during the stop closure. ♠♠ 1. Intro. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄ ►► 90 / 95

P. C. Pandey, EE Dept, IIT Bombay 6. Summary & Conclusions (2/3) ▪ Validation of estimated place of closure in VCV utterances with oral stops English: 6 stops (unvoiced/voiced, 3 places), 3 M & 2 F speakers Marathi: 5 stops (unvoiced, 5 places), 1 M speaker XRMB database with acoustic signals recorded during X-ray micro-beam imaging: 3 stops (unvoiced, 3 places), 20 M & 20 F speakers ▪ Improving the consistency of the shape estimation during fixed VT configuration without smearing during transitional segments Selection of Analysis frames positioned at the minima of the "windowed energy index" to reduce variability in the area values estimated by LP analysis during vowel segments with fixed-tract configurations. ♠♠ ►► 1. Intro. 2. Visual STA 91 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay 6. Summary & Conclusions (3/3) Future Work ▪ Application of the technique to recordings from a larger number of speakers with different age groups and language backgrounds. ▪ Application of the technique on recordings with vocal tract shapes simultaneously captured by imaging techniques. ▪ Investigations with shape estimation using other analysis techniques (e. g. formant tracking, articulatory analysis by synthesis). ▪ Development of speech training aid with dynamic display of vocal tract shape. ▪ Evaluation for speech training of hearing impaired ♠♠ 1. Intro. 2. children. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ►► 92 / 95 ◄◄

P. C. Pandey, EE Dept, IIT Bombay ♠♠ ►► 1. Intro. 2. Visual STA 93 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay Prem C. Pandey Prof. Pandey received the B. Tech. degree in electronics engineering from the Banaras Hindu University in 1979, the M. Tech. degree in electrical engineering from the Indian Institute of Technology Kanpur (India) in 1981, and the Ph. D. degree in biomedical engineering from the University of Toronto (Canada) in 1987. In 1987, he joined the University of Wyoming (USA) as an Assistant Professor in electrical engineering and later joined the Indian Institute of Technology Bombay in 1989, where he is a Professor in electrical engineering. He is also with the biomedical engineering program. His research interests include speech and signal processing; biomedical signal processing; embedded system design and electronic instrumentation. ♠♠ ►► 1. Intro. 2. Visual STA 94 / 95 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄

P. C. Pandey, EE Dept, IIT Bombay Signal Processing & Instrumentation Lab EE Dept, IIT Bombay http: //www. ee. iitb. ac. in/~spilab Impedance Cardiography • Development of impedance cardiograph • Artifact suppression in impedance cardiography Speech & Hearing • Low cost diagnostic audiometer & noise cancelling headphones • Impedance glottography • Enhancement of electrolaryngeal speech • Speech synthesis and voice transformation • Speech processing for hearing aids for sensorineural loss • Speech training aids for the hearing impaired ♠♠ 1. Intro. 2. Visual STA 3. LPC VTSE 4. VTSE DSC 5. Impro, VTS 6. Visual Disp. 7. Con. ♦♦ ◄◄ ►► 95 / 95