П 5 Применение производной к исследованию функций Теорема

П. 5. Применение производной к исследованию функций Теорема 2. 8. (признак монотонности или достаточное условие монотонности) Если функция y=f(x) дифференцируема на интервале (a, b) и f /(x) ≥ 0 (f /(x) ≤ 0) на (a, b) , то функция не убывает (не возрастает) на (a, b). Док-во: Рассмотрим случай, когда f /(x) ≥ 0. Пусть x 1, x 2 - две произвольные точки из интервала (a, b), причем x 1< x 2. Тогда на отрезке [x 1, x 2] для функции y=f(x) выполнены все условия теоремы Лагранжа. Следовательно, существует такая точка c∈[x 1, x 2] , в которой выполняется f(x 2)-f(x 1)=f /(c)(x 2 -x 1). По условию теоремы f /(c)≥ 0 и разность x -x ≥ 0, значит f(x )-f(x )≥ 0, из чего следует, что 2 1 функция не убывает на (a, b). Теорема доказана.

Теорема 2. 9. (достаточное условие локального экстремума) Пусть функция y=f(x) дифференцируема в некоторой - окрестности точки x 0. Тогда, если f /(x)>0 для всех x (x 0 - , x 0) и f /(x)<0 для всех x (x 0, x 0+ ), то x 0 - точка строго локального максимума. И наоборот, если f /(x)<0 для всех x (x 0 - , x 0), а для всех x (x 0, x 0+ ) f /(x)>0, то x 0 - точка строго локального минимума. Другими словами, если при переходе через точку производная функции меняет свой знак с плюса на минус, то x 0 - точка строго локального максимума, если с минуса на плюс, то x 0 - точка строго локального минимума, если же производная вообще не меняет своего знака, то в точке нет экстремума.

Алгоритм исследования функции на монотонность и точки экстремума 1. Найти производную функции f /(x). 2. Найти стационарные и критические точки функции, т. е. точки, в которых производная равна нулю или не существует, решив уравнение f /(x)=0. 3. Нанести эти точки на числовую прямую, разбивая ее на промежутки. 4. На каждом промежутке вычислить знак производной. 5. Сделать выводы промежутки монотонности и точки экстремума в соответствии с теоремами 2. 8 и 2. 9.

Теорема 2. 10 (второе достаточное условие экстремума) Пусть для функции y=f(x) в точке x 0 выполняется f /(x 0)=0 и в этой точке существует вторая производная функции. Тогда если f //(x 0)>0, то x 0 - точка минимума, если f //(x 0)<0, то x 0 - точка максимума. Пример: исследовать функцию на монотонность и точки экстремума y=x 3 -9 x 2+24 x.

П. 6. Исследование функции на выпуклость и точки перегиба ОПР. 2. 2. Функция y=f(x), непрерывная на отрезке [a, b] и дифференцируемая в интервале (a, b), называется выпуклой вверх (вниз) на этом отрезке, если при a x b график функции лежит не выше (не ниже) касательной, проведенной в любой точке отрезка [a, b] к графику функции. Теорема 2. 11. (достаточное выпуклости функции) условие направления Если функция y=f(x) имеет на интервале (a, b) вторую производную и f //(x) 0 на этом интервале, то функция выпукла вниз на этом интервале, если f //(x) 0, то функция выпукла вверх на (a, b).

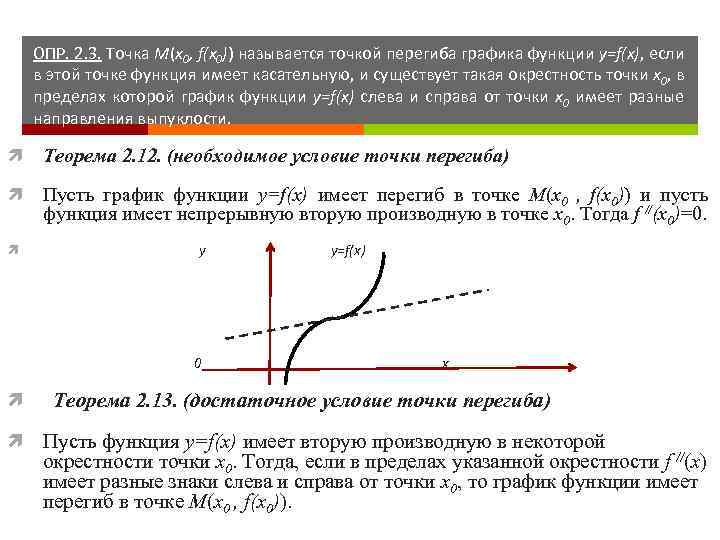ОПР. 2. 3. Точка M(x 0, f(x 0)) называется точкой перегиба графика функции y=f(x), если в этой точке функция имеет касательную, и существует такая окрестность точки x 0, в пределах которой график функции y=f(x) слева и справа от точки x 0 имеет разные направления выпуклости. Теорема 2. 12. (необходимое условие точки перегиба) Пусть график функции y=f(x) имеет перегиб в точке M(x 0 , f(x 0)) и пусть функция имеет непрерывную вторую производную в точке x 0. Тогда f //(x 0)=0. y 0 y=f(x) x Теорема 2. 13. (достаточное условие точки перегиба) Пусть функция y=f(x) имеет вторую производную в некоторой окрестности точки x 0. Тогда, если в пределах указанной окрестности f //(x) имеет разные знаки слева и справа от точки x 0, то график функции имеет перегиб в точке M(x 0 , f(x 0)).

Общая схема исследования свойств функции и построения ее графика Найти область определения функции. Исследовать функцию на периодичность. Исследовать функцию на четность. Найти точки пересечения графика с осями координат и определить интервалы знакопостоянства функции; найти точки разрыва и установить характер разрыва. 5. Исследовать поведение функции на границах области определения, найти асимптоты. 6. Найти промежутки возрастания и убывания функции, точки экстремума. 7. Исследовать направления выпуклости графика функции, найти точки перегиба. 8. Составить таблицу значений функций для некоторых значений ее аргумента. 9. Используя все полученные результаты, построить график функции. Замечания: 1) необходимо все шаги исследования отражать на координатной плоскости; 2) график функции должен быть схематично построен до вычисления первой производной функции. 1. 2. 3. 4.

П. 7. Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке Пусть функция y=f(x) непрерывна на отрезке [a, b]. Тогда она 1. 2. 3. 4. достигает на этом промежутке своих наибольшего и наименьшего значений. Как найти эти значения? Достигать своих наибольшего и наименьшего значений функция может как внутри отрезка, так и на его концах. Если функция достигает этих значений внутри отрезка, то это должно происходить в точке экстремума. Поэтому для нахождения наибольшего и наименьшего значений непрерывной функции на отрезке действуют согласно следующему алгоритму: найти производную функции y /(x), найти стационарные и критические точки (где y /(x)=0 или не существует), отобрать те точки, которые лежат внутри отрезка [a, b], вычислить значения функции в отобранных точках и на концах отрезка, выбрать из них наибольшее и наименьшее.