Overview Trie Types of Trie

Overview

Trie

Types of Trie

Standard Trie Approach Each node (except root) is labeled with a character Children of node are ordered (alphabetically) Paths from root to leaves yield all input strings

Standard Trie Example For strings { a, and, any, at }

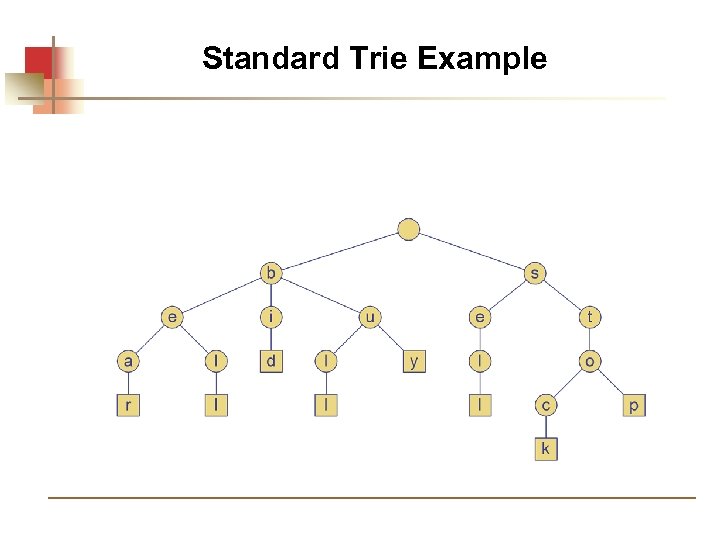Standard Trie Example

Standard Tries

Standard Tries

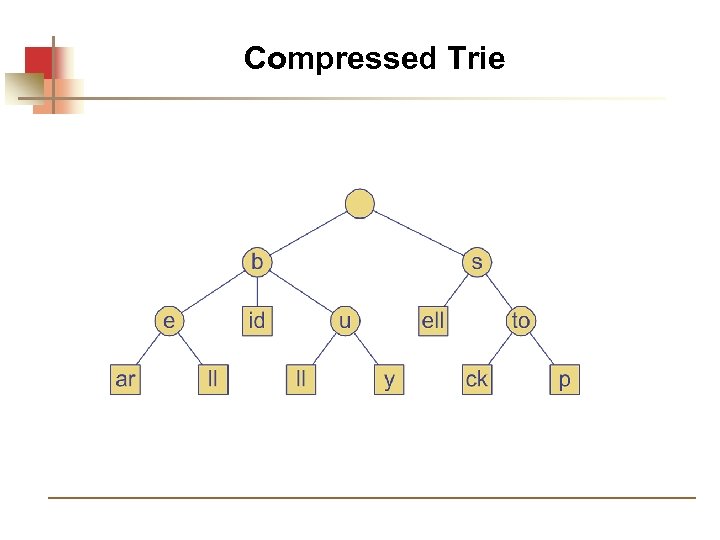Compressed Trie

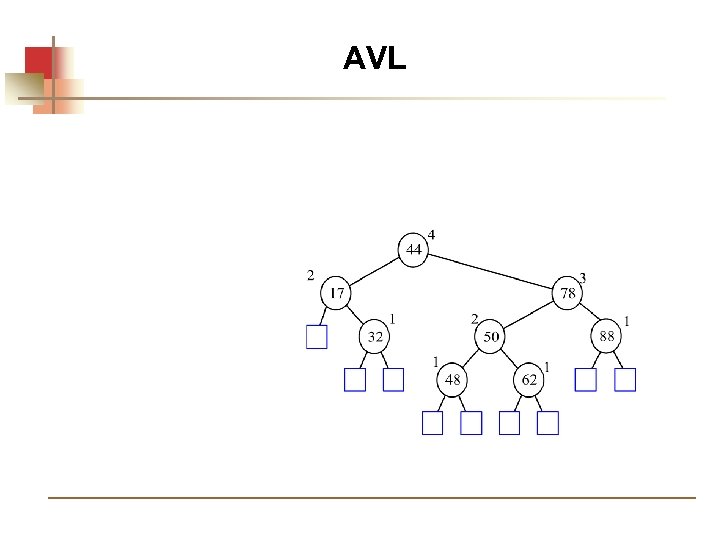AVL

Height of an AVL Tree

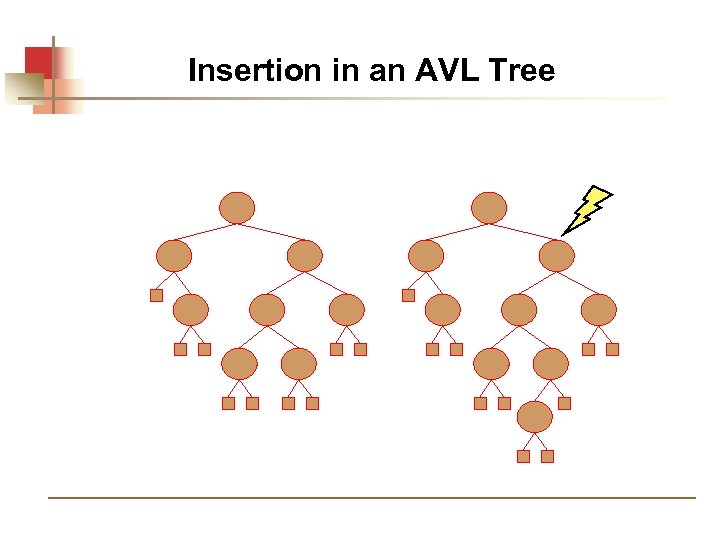Insertion in an AVL Tree

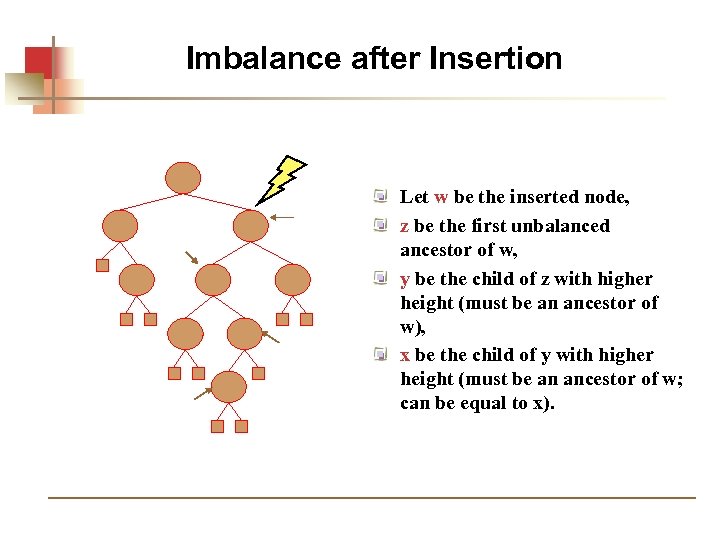Imbalance after Insertion Let w be the inserted node, z be the first unbalanced ancestor of w, y be the child of z with higher height (must be an ancestor of w), x be the child of y with higher height (must be an ancestor of w; can be equal to x).

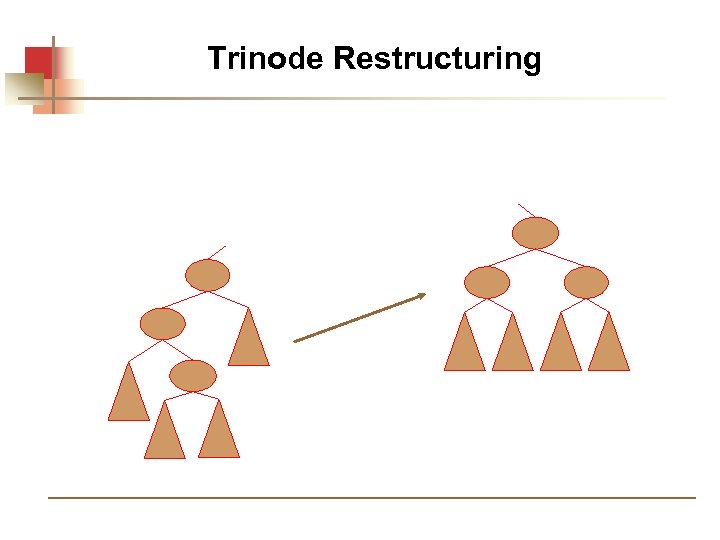
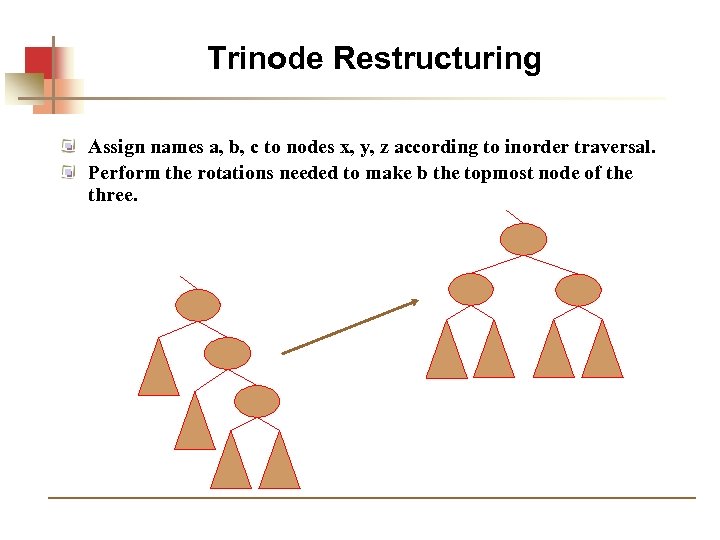Trinode Restructuring Assign names a, b, c to nodes x, y, z according to inorder traversal. Perform the rotations needed to make b the topmost node of the three.

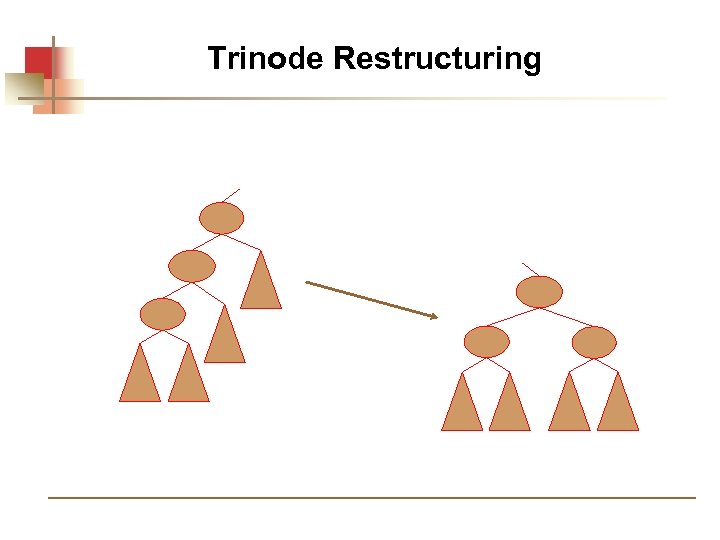Trinode Restructuring

Trinode Restructuring

Trinode Restructuring

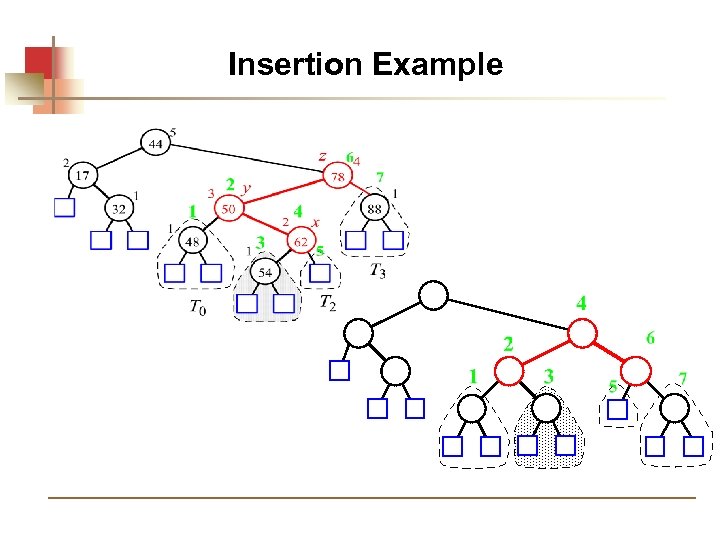Insertion Example

Removal in an AVL Tree Removal begins as in a binary search tree, which means the node removed will become an empty external node. Its parent w may cause an imbalance.

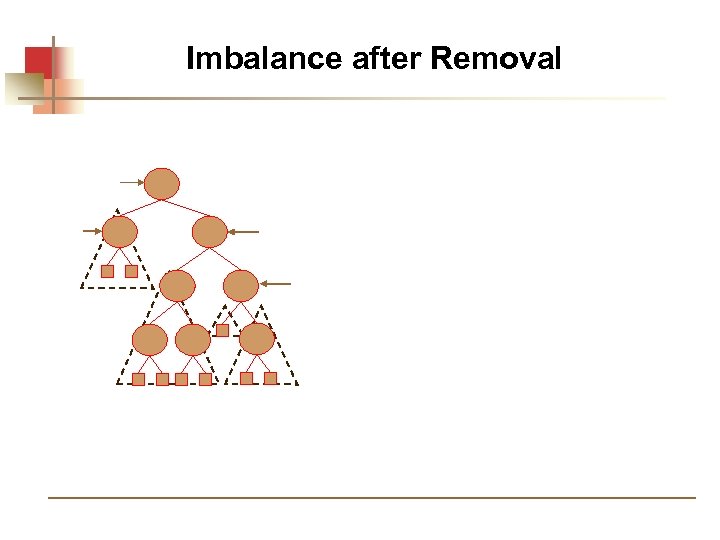Imbalance after Removal

Rebalancing after a Removal Assign names a, b, c to nodes x, y, z according to inorder traversal. Perform rotations to make b the topmost of the three. As this restructuring may upset the balance of another node higher in the tree, we must continue checking for balance until the root of T is reached.

Repeated Rebalancing

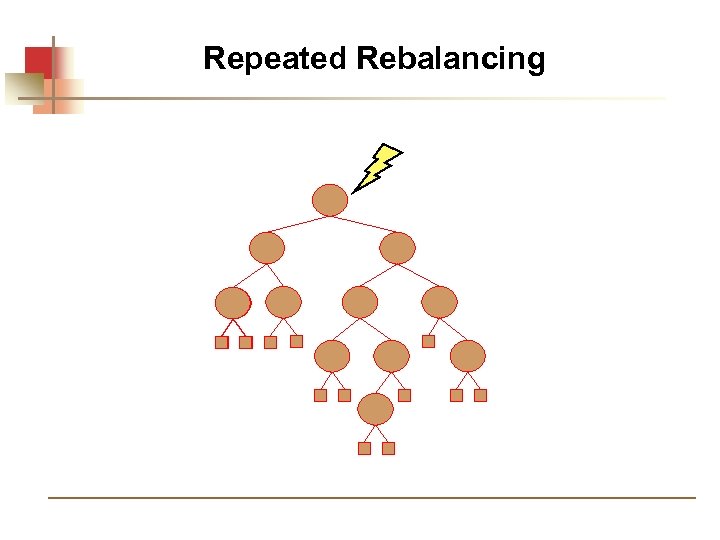Repeated Rebalancing

Running Times for AVL Trees

Red-Black Trees

Red-Black Properties

Red-Black Trees

Height of Red-Black Trees

RB Trees: Proving Height Bound

RB Trees: Proving Height Bound

RB Trees: Proving Height Bound

RB Trees: Proving Height Bound

RB Trees: Worst-Case Time