22bcc53a122e6e96f6f52de50943268d.ppt
- Количество слайдов: 20

Overview of Carbon Nanotubes II PHYS 570 X Carbon nanophysics Prof. Yong P. Chen 02/2/2009

Some one asked about grading policy • >50 pts should be sufficient to pass • >80 pts likely to be sufficient for A • There are (intentionally so) more than one ways to earn points that suit your background/interests

Upcoming Journal Club Presentations • Deepak Pandey: Environmental/Health effects of CNT? Date: • John Watson: Coulomb collapse in graphene; Date: • Jonathan Claussen: Brownian motion of CNTs in fluids; Date: [Please post the papers in your wikipage] • Anyone else?

More recent news on CNT: • P. Avouris: “Carbon nanotube electronics and photonics”, Phys. Today (Jan. 2009) • Separation of CNTs Realized : L. Zhang (Hongjie Dai Grp, Stanford) et al. , Optical Characterizations and Electronic Devices of Nearly Pure (10, 5) Single-Walled Carbon Nanotubes, ar. Xiv: 0902. 0010 (2009) Optical properties of CNTs: • Tony Heiz (Columbia) • Bruce Weissman (Rice) Raman properties: Dresselhaus et al. , Adv. Phys (2002)

Physics of Graphite etc. • http: //en. wikipedia. org/wiki/Graphite • http: //www. azom. com/details. asp? Article. ID=1630 • Pierson H. O. Handbook of carbon, graphite, diamond and fullerenes--- Properties, Processing and Applications (Noyes Publications, Park Ridge, 1993). [everything up to 1993] • Chemistry and Physics of Carbon, P. L. Walker, Editor. • Brian T. Kelly, “Physics of Graphite” (1981) • N. B. Brandt, S. M. Chudinov and YG Ponomarev, Semimetals 1: Graphite and its compounds (1988) • T. Enoki, M. Suzuki and M. Endo, “Graphite intercalation compounds and applications” (2003)

Types of Graphite Major commercial sources: http: //www. asbury. com/ (also contains good introduction to carbon) http: //www. advceramics. com/ (formerly union carbide) Types: • Natural graphite • Expandable graphite http: //www. powersourcing. com/sf/expandablegraphite. htm • Kish graphite • HOPG (highly ordered porolytic graphite) “A-B stacking” STM image of HOPG (ex. Why do you see only 1 sub-lattice”? )

Graphite: Electronic Properties Basic properties/bandstructures: The Band Theory of Graphite P. R. Wallace, Phys Rev (1947) Band Structure of Graphite J. C. Slonczewski and P. R. Weiss, Phys Rev (1958) Band Structure of Graphite and de Haas-van Alphen Effect, J. W. Mc. Clure, Phys Rev (1957) Mc. Clure, IBM Journal (1964) [a copy in PHYS 570 X “Reading Materials”] Tyler and Wilson, Thermal Conductivity, Electrical Resistivity, and Thermoelectric Power of Graphite , Phys. Rev (1953) Optical Properties of Graphite E. A. Taft and H. R. Philipp, Phys Rev (1965)

Graphite: Electronic Properties (cont. ) • CA Klein, Electrical Properties of Pyrolytic graphite, Rev. Mod. Phys. (1962) Magneto-transport: • Y Koike et al. , Weak localization of graphite, J. Phys. Soc. Jap. (1985) • X. Du et al. , Metal-insulator-like behavior in semimetallic bismuth and graphite, PRL (2005) • Kopelevich et al. , Reentrant metallic behavior of graphite in the quantum limit, PRL 2003 • Electric and thermal electric transport: T. Tokumoto et al. , Solid State Comm. (2004)

Bucky. Balls (C-60 etc. ) • Nobel lectures and biographies: http: //nobelprize. org/nobel_prizes/chemistry/l aureates/1996/ • http: //en. wikipedia. org/wiki/Fullerene • MS Dresselhaus, G. Dresselhaus and PC Eklund, Science of Fullerenes and Carbon nanotubes (1996) • Roger Taylor & David R. M. Walton, “The Chemistry of Fullerenes”, Nature (1993)

Buckyballs (cont. ) Electronic properties: Electronic properties of doped fullerenes L. Mihaly and L Forro, Reports on Progress in Physics, 64, 649 -700 (2001) Superconductivity: A. Hebard et al. , Superconductivity at 18 K in potassiumdoped C 60, Nature (1991) See also --- later work on “superconductivity” in CNTs: "Superconductivity in 4 Angstrom Single-Walled Carbon Nanotubes", Z. K. Tang, Lingyun Zhang, N. Wang, X. X. Zhang, G. H. Wen, G. D. Li, J. N. Wang, C. T. Chan, and Ping Sheng, Science 292, 2462 -2465

Quick Review of 2 DES and Quantum Hall Effects • 2 D electron systems (2 DES) in semiconductors • Historical developments: the quest of new states at high B: Wigner cystals, IQHE, FQHE etc. A “lay person” lecture by Jim Eisenstein: http: //online. kitp. ucsb. edu/online/spintr 2_c 06/eisenstein/
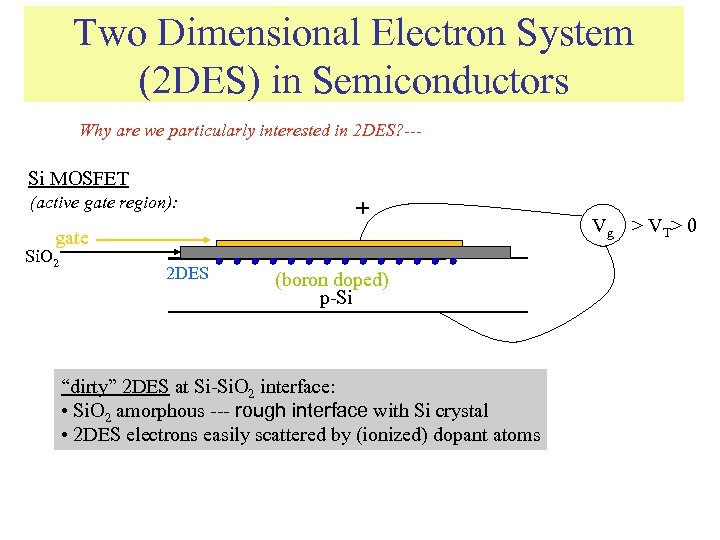
Two Dimensional Electron System (2 DES) in Semiconductors Why are we particularly interested in 2 DES? --- Si MOSFET (active gate region): + gate Si. O 2 2 DES (boron doped) p-Si “dirty” 2 DES at Si-Si. O 2 interface: • Si. O 2 amorphous --- rough interface with Si crystal • 2 DES electrons easily scattered by (ionized) dopant atoms Vg > VT> 0

High Quality 2 DES in Semiconductor Heterostructures Quantum Well (QW) Si Alx. Ga 1 -x. As Si • Molecular Beam Epitaxy (A. Cho etc. , ~1970) cf. Klaus Ploog, “Molecular Beam Epitaxy” in http: //www. aps. org/units/fiap/presentations/icps 04. cfm N. G. Einspruch ed. Heterostructures and Quantum e- Alx. Ga 1 -x. As Ec Ga. As-Al(Ga)As: • lattice a~5. 7 Å Devices (Ch. 2) • Modulation Doping (H. Stomer etc. , ~1978) Ga. As (B) • Quantization of z-motion (only one energy level occupied at low T) ==> 2 DES in xy plane Ex. For a QW of typical width of 30 nm, use poor man’s way to estimate the typical energy level separation; compare it with the typical experiments’ temperature (~100 m. K).

Magnetic Field Induced Wigner Solid B cyclotron freq. c = e. B/m* cyclotron radius Rc = m /e. B § Wigner Solid (“MIWS”) expected at sufficiently large B (Lozovik & Yudson, JETP, 1975) ----when kinetic energy is quenched and interaction dominates (Wigner 1934) Ex. Take ~ f, and assume Rc must be less than some fraction of inter-electron separation (take a poor man’s guess, say 5%) for WS to occur, estimate how strong the magnetic field need to be.
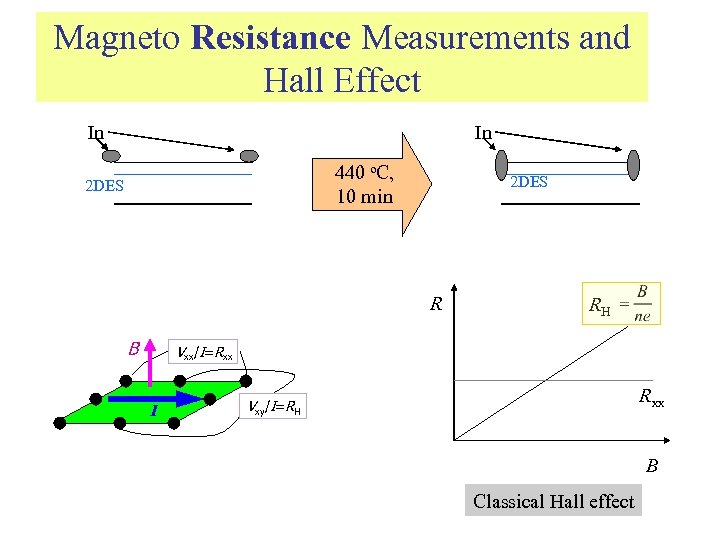
Magneto Resistance Measurements and Hall Effect In In 440 o. C, 10 min 2 DES R B RH Vxx/I=Rxx I Rxx Vxy/I=RH B Classical Hall effect
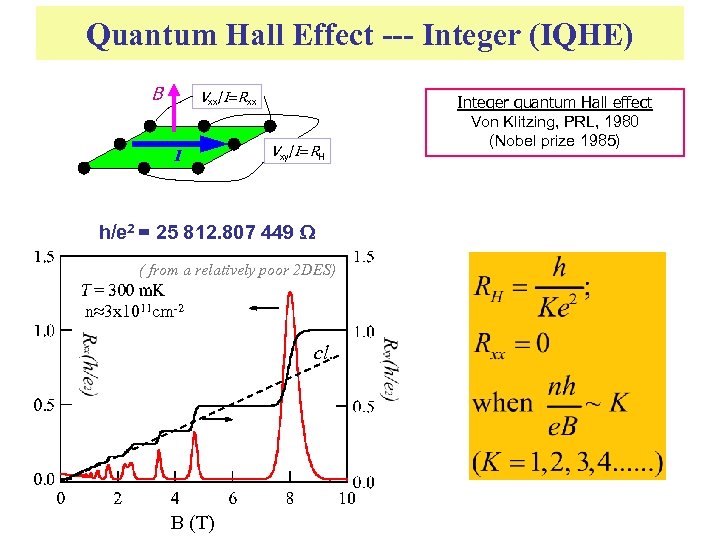
Quantum Hall Effect --- Integer (IQHE) B Vxx/I=Rxx I Vxy/I=RH h/e 2 = 25 812. 807 449 ( from a relatively poor 2 DES) n≈3 x 1011 cm-2 cl. B (T) Integer quantum Hall effect Von Klitzing, PRL, 1980 (Nobel prize 1985)
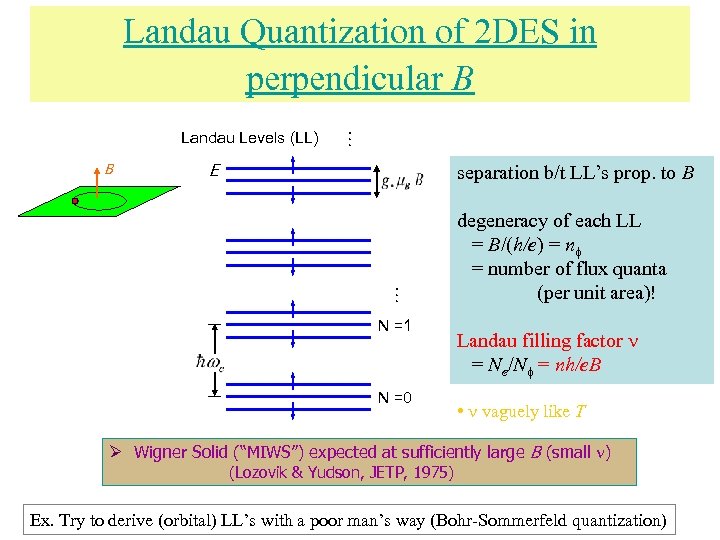
Landau Levels (LL) E separation b/t LL’s prop. to B … Landau Quantization of 2 DES in perpendicular B N =1 N =0 degeneracy of each LL = B/(h/e) = number of flux quanta (per unit area)! Landau filling factor = Ne/N = nh/e. B • vaguely like T Ø Wigner Solid (“MIWS”) expected at sufficiently large B (small ) (Lozovik & Yudson, JETP, 1975) Ex. Try to derive (orbital) LL’s with a poor man’s way (Bohr-Sommerfeld quantization)
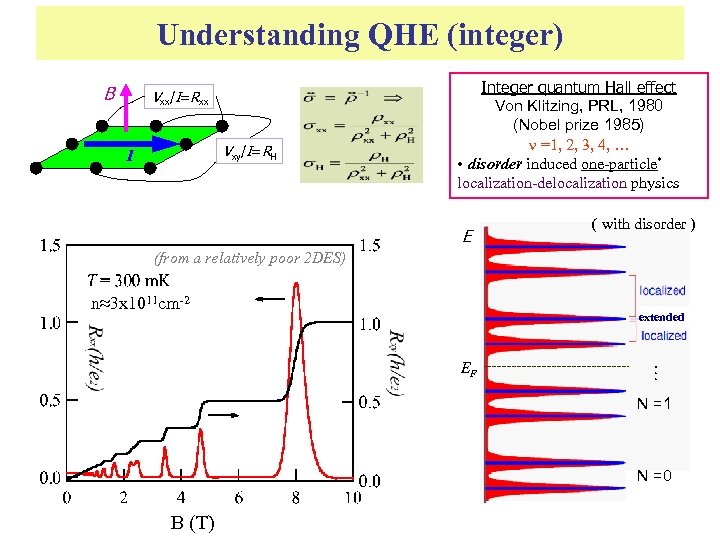
Understanding QHE (integer) B Vxx/I=Rxx Vxy/I=RH I Integer quantum Hall effect Von Klitzing, PRL, 1980 (Nobel prize 1985) =1, 2, 3, 4, … • disorder induced one-particle* localization-delocalization physics E ( with disorder ) (from a relatively poor 2 DES) n≈3 x 1011 cm-2 EF … extended N =1 N =0 B (T)
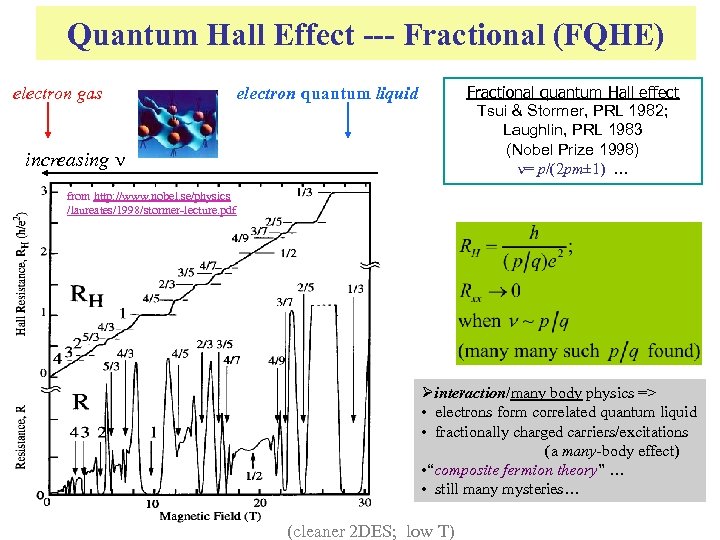
Quantum Hall Effect --- Fractional (FQHE) electron gas Fractional quantum Hall effect Tsui & Stormer, PRL 1982; Laughlin, PRL 1983 (Nobel Prize 1998) = p/(2 pm± 1) … electron quantum liquid increasing from http: //www. nobel. se/physics /laureates/1998/stormer-lecture. pdf Øinteraction/many body physics => • electrons form correlated quantum liquid • fractionally charged carriers/excitations (a many-body effect) • “composite fermion theory” … • still many mysteries… (cleaner 2 DES; low T)
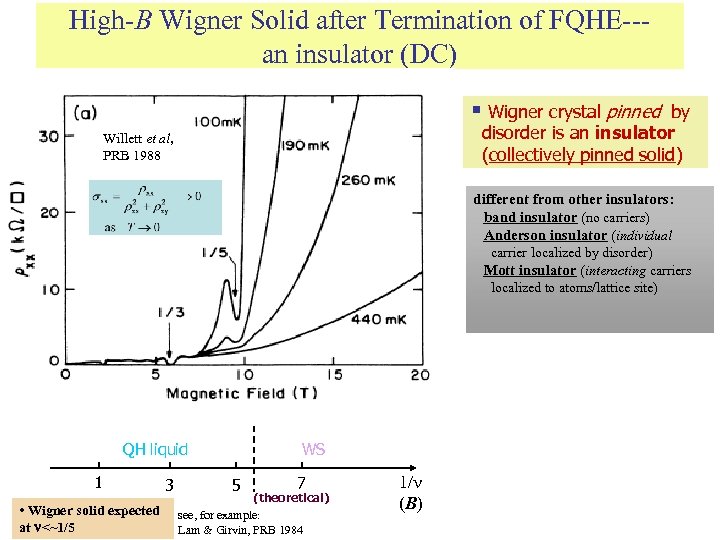
High-B Wigner Solid after Termination of FQHE--an insulator (DC) § Wigner crystal pinned by disorder is an insulator (collectively pinned solid) Willett et al, PRB 1988 different from other insulators: band insulator (no carriers) Anderson insulator (individual carrier localized by disorder) Mott insulator (interacting carriers localized to atoms/lattice site) QH liquid 1 • Wigner solid expected at <~1/5 3 WS 5 7 (theoretical) see, for example: Lam & Girvin, PRB 1984 1/ (B)
22bcc53a122e6e96f6f52de50943268d.ppt