Overview of Artificial Intelligence Thomas R Ioerger Associate

Overview of Artificial Intelligence Thomas R. Ioerger Associate Professor Department of Computer Science Texas A&M University

What is AI? • Real applications, not science fiction – Control systems, diagnosis systems, games, interactive animations, combat simulations, manufacturing scheduling, transportation logistics, financial analysis, computer-aided tutoring, searchand-rescue robots

Different Perspectives • Philosophical perspective – What is the nature of “intelligence”? Can a machine/program ever be truly “intelligent”? – Strong AI hypothesis: Is acting intelligently sufficient? – laws of thought; rational (ideal) decision-making • Socrates is a man; men are mortal; therefore, Socrates is mortal • Psychological perspective – What is the nature of “human intelligence”? – Cognitive science – concept representations, internal world model, information processing metaphor – role of ST/LT memory? visualization? emotions? analogy? creativity? – build programs to simulate inference, learning. . .

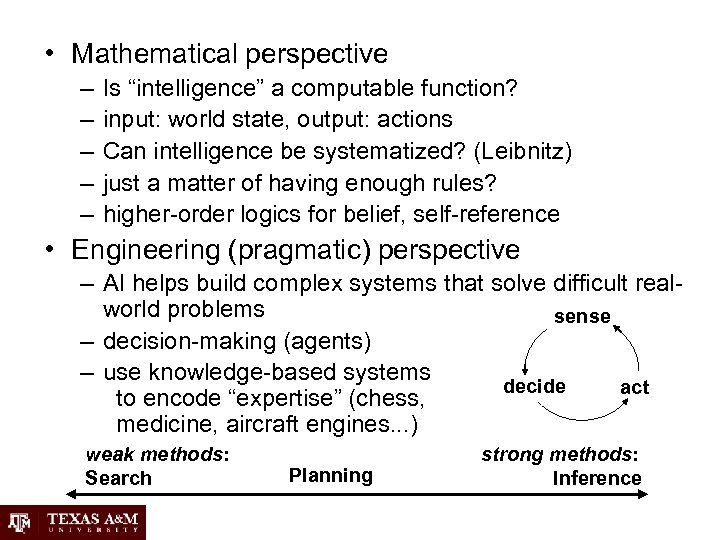• Mathematical perspective – – – Is “intelligence” a computable function? input: world state, output: actions Can intelligence be systematized? (Leibnitz) just a matter of having enough rules? higher-order logics for belief, self-reference • Engineering (pragmatic) perspective – AI helps build complex systems that solve difficult realworld problems sense – decision-making (agents) – use knowledge-based systems decide act to encode “expertise” (chess, medicine, aircraft engines. . . ) weak methods: Search Planning strong methods: Inference

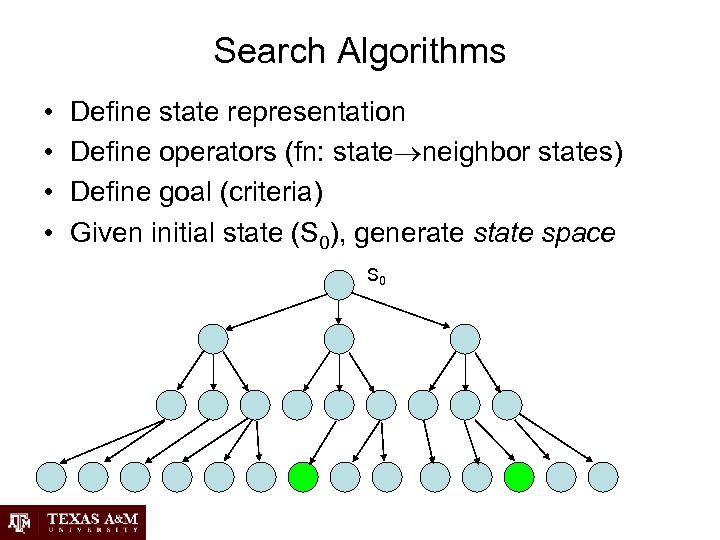Search Algorithms • • Define state representation Define operators (fn: state neighbor states) Define goal (criteria) Given initial state (S 0), generate state space S 0

Many problems can be modeled as search • tic-tac-toe – states=boards, operator=moves • symbolic integration – states=equations, opers=algebraic manipulations • class schedule – states=partial schedule, opers=add/remove class • rock band tour (traveling salesman problem) – states=order of cities to visit, opers=swap order • robot-motion planning – states=robot configuration, opers=joint bending

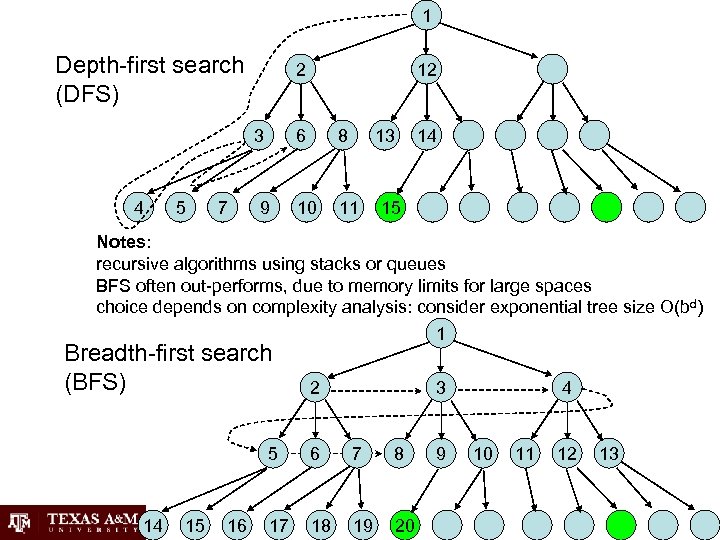1 Depth-first search (DFS) 2 3 4 5 7 12 6 9 8 13 10 11 14 15 Notes: recursive algorithms using stacks or queues BFS often out-performs, due to memory limits for large spaces choice depends on complexity analysis: consider exponential tree size O(bd) 1 Breadth-first search (BFS) 2 5 6 7 8 17 18 19 20 14 15 16 3 9 4 10 11 12 13

Heuristics • give guidance to search in terms of which nodes look “closest to the goal” – node evaluation function – h(n)=w 1*(piece_differential)+w 2*(center_control)+ w 3*(#pieces_can_be_taken)+w 4*(#kings) • greedy algorithms search these nodes first • bias direction of search to explore “best” parts of state space (most likely to contain goal) • A* algorithm – optimal (under certain conditions) – finds shortest path to a goal – insensitive to errors in heuristic function

Specialized Search Algorithms • Game-playing – two-player zero-sum games (alternate moves) – minimax algorithm: form of “look-ahead” – If I make a move, how will opponent likely respond? Which move leads to highest assured payoff? • Constraint-satisfaction problems (CSPs) – state=partial variable assignment – goal find assignment that satisfies constraints – algorithms use back-tracking, constraint propagation, and heuristics – pre-process constraint-graph to make more efficient – examples: map-coloring, propositional satisfiability, server configuration

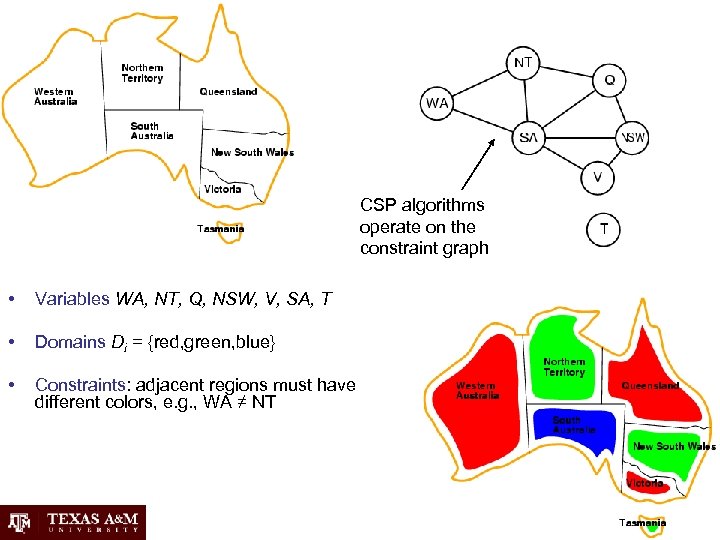CSP algorithms operate on the constraint graph • Variables WA, NT, Q, NSW, V, SA, T • Domains Di = {red, green, blue} • Constraints: adjacent regions must have different colors, e. g. , WA ≠ NT

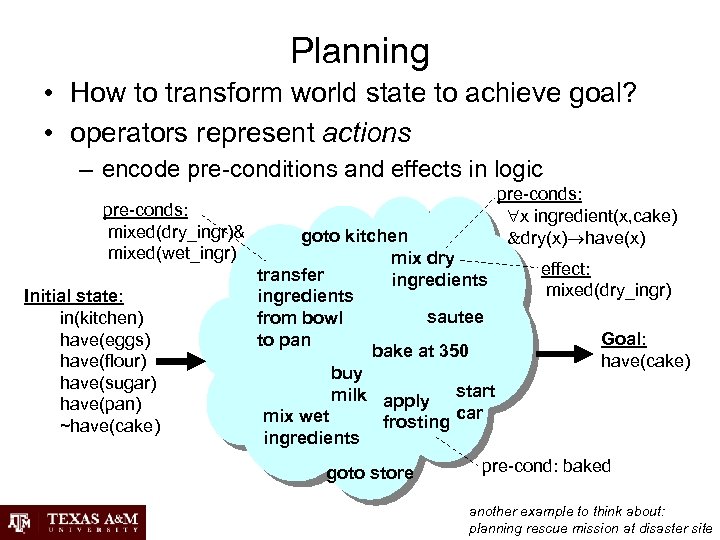Planning • How to transform world state to achieve goal? • operators represent actions – encode pre-conditions and effects in logic pre-conds: mixed(dry_ingr)& mixed(wet_ingr) Initial state: in(kitchen) have(eggs) have(flour) have(sugar) have(pan) ~have(cake) goto kitchen mix dry transfer ingredients sautee from bowl to pan bake at 350 buy milk apply start car mix wet frosting ingredients goto store pre-conds: x ingredient(x, cake) dry(x) have(x) effect: mixed(dry_ingr) Goal: have(cake) pre-cond: baked another example to think about: planning rescue mission at disaster site

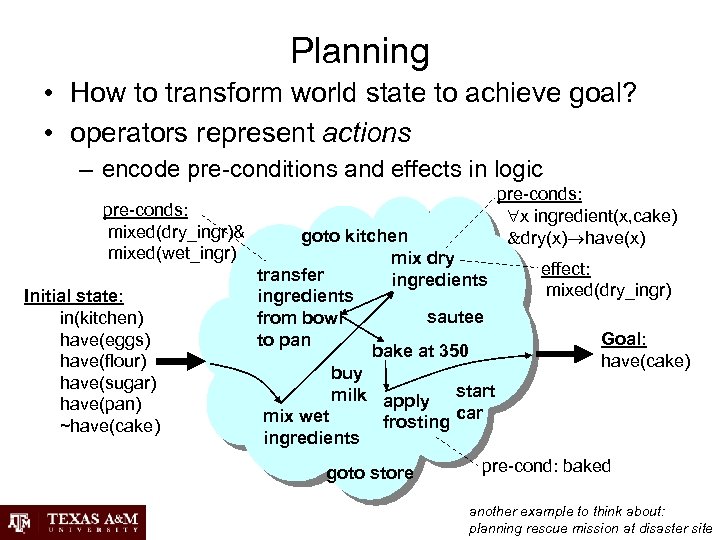Planning • How to transform world state to achieve goal? • operators represent actions – encode pre-conditions and effects in logic pre-conds: mixed(dry_ingr)& mixed(wet_ingr) Initial state: in(kitchen) have(eggs) have(flour) have(sugar) have(pan) ~have(cake) goto kitchen mix dry transfer ingredients sautee from bowl to pan bake at 350 buy milk apply start car mix wet frosting ingredients goto store pre-conds: x ingredient(x, cake) dry(x) have(x) effect: mixed(dry_ingr) Goal: have(cake) pre-cond: baked another example to think about: planning rescue mission at disaster site

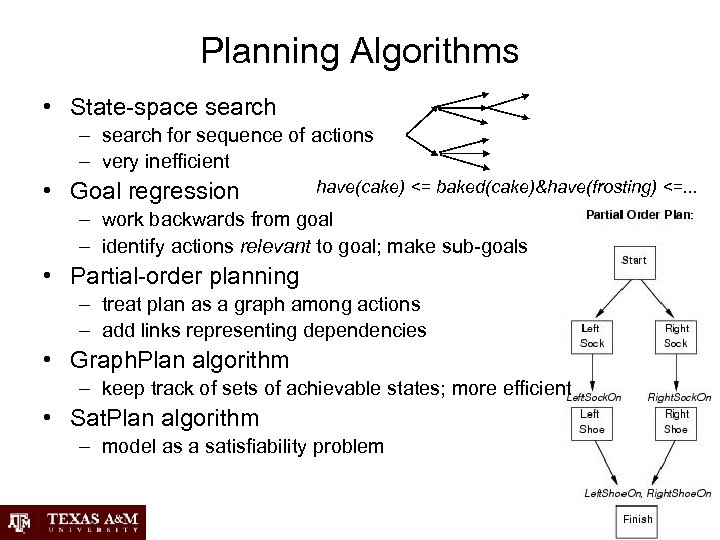Planning Algorithms • State-space search – search for sequence of actions – very inefficient • Goal regression have(cake) <= baked(cake)&have(frosting) <=. . . – work backwards from goal – identify actions relevant to goal; make sub-goals • Partial-order planning – treat plan as a graph among actions – add links representing dependencies • Graph. Plan algorithm – keep track of sets of achievable states; more efficient • Sat. Plan algorithm – model as a satisfiability problem

Knowledge-Based Methods • need: representation for search heuristics and planning operators • need expertise to produce expert problem-solving behavior • first-order logic – a formal language for representing knowledge • rules, constraints, facts, associations, strategies. . . – – rain(today) wet(road) fever infection in(class_C_air_space) reduce(air_speed, 150 kts) can(take_opp_queen, X)&~losing_move(X) do(X) • use knowledge base (KB) to infer what to do – goals & initial_state & KB do(action) – need inference algorithms to derive what is entailed • declarative vs. procedural programming

First-Order Logic • lingua franca of AI • syntax – predicates (relations): author(Candide, Voltaire) – connectives: & (and), v (or), ~ (not), (implies) – quantified variables: X person(X) Y mother(X, Y) • Ontologies – systems of concepts for writing KBs – categories of stuff (solids, fluids, living, mammals, food, equipment. . . ) and their properties – places (in), part_of, measures (volume) – domain-dependent: authorship, ambush, infection. . . – time, action, processes (Situation Calculus, Event Logic) – beliefs, commitments • issues: granularity, consistency, expressiveness

Inference Algorithms D A&B D • Natural deduction B – search for proof of query A Bv. C ~C – use rules like modus ponens (from A and A B, get B) • Backward-chaining – start with goal, reduce to sub-goals – complete only for definite-clause KBs (rules with conjunctive antecedents) • Resolution Theorem-proving – – convert all rules to clauses (disjunctions) {Av. B, ~Bv. C} Av. C keeping resolving clauses till produce empty clause complete for all FOL KBs

Prolog and Expert Systems • Automated deduction systems • programming = writing rules • make query, system responds with true/false plus variable bindings • inference algorithm based on backward-chaining

Prolog example sibling(X, Y) : - parent(Z, X), parent(Z, Y). grandfather(X, Y) : - father(X, Z), parent(Z, Y). parent(X, Y) : - father(X, Y). parent(X, Y) : - mother(X, Y). mother(tracy, sally). father(bill, erica). father(mike, bill). ? - sibling(sally, erica). Yes ? - grandfather(sally, X). grandfather(sally, mike)

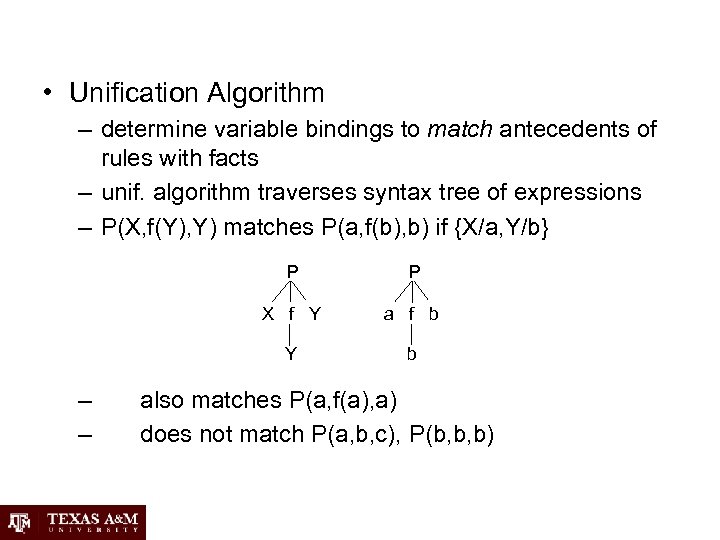• Unification Algorithm – determine variable bindings to match antecedents of rules with facts – unif. algorithm traverses syntax tree of expressions – P(X, f(Y), Y) matches P(a, f(b), b) if {X/a, Y/b} P X f Y a f b Y – – P b also matches P(a, f(a), a) does not match P(a, b, c), P(b, b, b)

• Managing Uncertainty in real expert systems – – default/non-monotonic logics (assumptions) certainty factors (degrees of beliefs) probabilistic logics Bayesian networks (causal influences) • Complexity of inference? – suitable for real-time applications?

Application of Data Structures and Algorithms in AI • • • priority queues in search algorithms recursion in search algorithms shortest-path algorithm for planning/robotics hash tables for indexing rules by predicate in KBS dynamic programming to improve efficiency of theorem-provers (caching intermediate inferences) • graph algorithms for constraint-satisfaction problems (arc-consistency) • complexity analysis to select search algorithm based on branching factor and depth of solution for a given problem

Use of AI in Research • intelligent agents for flight simulation – collaboration with Dr. John Valasek (Aerospace Eng. ) – goal: on-board decision-making without ATC – approach: use 1) multi-agent negotiation, 2) reinforcement learning • pattern recognition in protein crystallography – collaboration with Dr. James Sacchettini (Biochem. ) – goal: automate determination of protein structures from electron density maps – approach: extract features representing local 3 D patterns of electron density and use to recognize amino acids and build – uses neural nets, and heuristics encoding knowledge of typical protein conformations and contacts

• TAMU courses on AI – CPSC 420/625 – Artificial Intelligence – undergrad • CPSC 452 – Robotics and Spatial Intelligence • also related: CPSC 436 (HCI) and CPSC 470 (IR) – graduate • • • CPSC 609 - AI Approaches to Software Engineering* CPSC 631 – Agents/Programming Environments for AI CPSC 632 - Expert Systems* CPSC 633 - Machine Learning CPSC 634 Intelligent User Interfaces CPSC 636 - Neural Networks CPSC 639 - Fuzzy Logic and Intelligent Systems CPSC 643 Seminar in Intelligent Systems and Robotics CPSC 644 - Cortical Networks CPSC 666 – Statistical Pattern Recognition (not official yet) Special Topics courses (CPSC 689). . . * = not actively taught

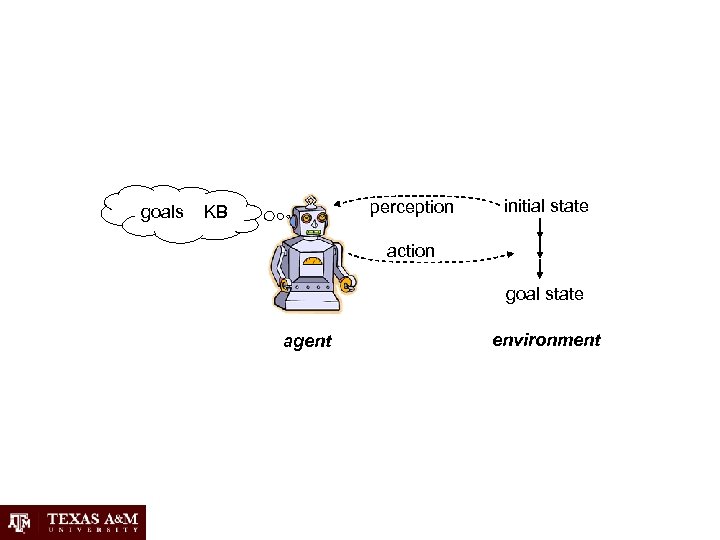goals perception KB initial state action goal state agent environment