04a58ab51a7a439b7458628201b73e74.ppt
- Количество слайдов: 21

Overconfidence and Prediction Bias in Political Stock Markets Carsten Schmidt (joint work with Michael Berleman, ifo Institute Dresden) School of Business and Economics Humboldt University Berlin cschmidt@wiwi. hu-berlin. de

The Puzzle l US political stock markets were very successful in predicting the election results – – l IEM predict result of the presidential election Bush/Dukakis 1988 with a MAE of 0. 2% (Forsythe et al. , 1992, AER) Forsythe et al. , 1997, JEBO European election markets were not (significantly) better than polls. Relatively higher MAE compared to US markets. – – Netherlands: Jacobsen et al. , 2000, EER Austria: Ortner Sweden: Bohm and Sonnegard, 1999, Scan. JE Germany: Berlemann und Schmidt (this meta-study) MAE PSM 1. 394, Polls 1. 524, (T=1. 198, p <0. 126)

Driving forces l Institutions – Election system v – Polls v l – Empirical contribution (Berg et al. , 1997) Number of different contracts (candidates/parties) is highly correlated with MAE Contract level: overconfidence Bias – – l Adjusted vs. raw data Market level: market complexity – l Proportional representation vs. Winner- takes-all Theoretical contribution (Jacobsen et al. , 2000, EER Overvaluation of small contracts, undervaluation of relatively large contracts Disparity of different contracts Bias not significant in US data (Forsythe et al. , 1999, JEBO) Trader level – Individual mistakes do not bias prediction in US data
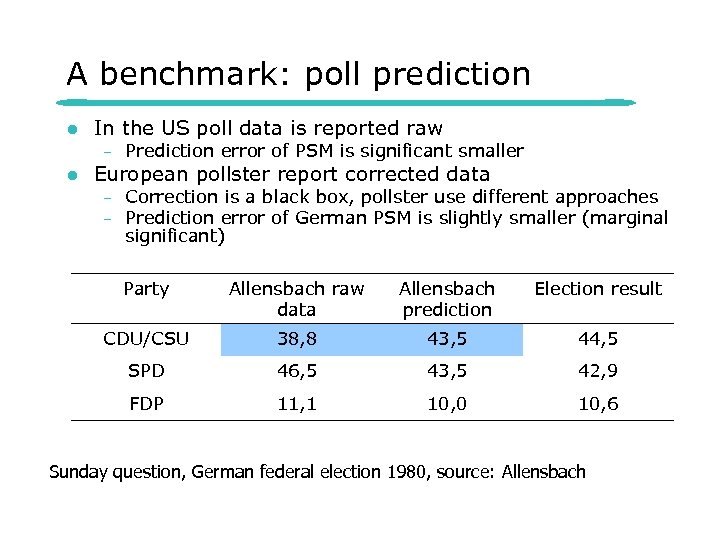
A benchmark: poll prediction l In the US poll data is reported raw – l Prediction error of PSM is significant smaller European pollster report corrected data – – Correction is a black box, pollster use different approaches Prediction error of German PSM is slightly smaller (marginal significant) Party Allensbach raw data Allensbach prediction Election result CDU/CSU 38, 8 43, 5 44, 5 SPD 46, 5 43, 5 42, 9 FDP 11, 1 10, 0 10, 6 Sunday question, German federal election 1980, source: Allensbach

Meta study German data l l Method: Empirical meta study Data: Final prediction of all German election markets (and all corresponding public polls for the election) – – Vote share markets Homogeous in the number of contracts (parties) v CDU, SPD, Grüne, FDP, PDS, Rep, Rest – of Field Different organizer (academia, commercial)
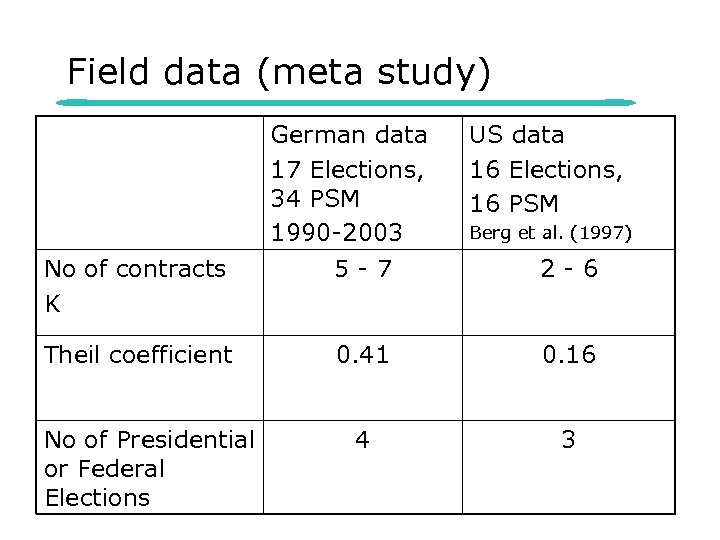
Field data (meta study) German data 17 Elections, 34 PSM 1990 -2003 US data 16 Elections, 16 PSM Berg et al. (1997) No of contracts K 5 -7 2 -6 Theil coefficient 0. 41 0. 16 4 3 No of Presidential or Federal Elections
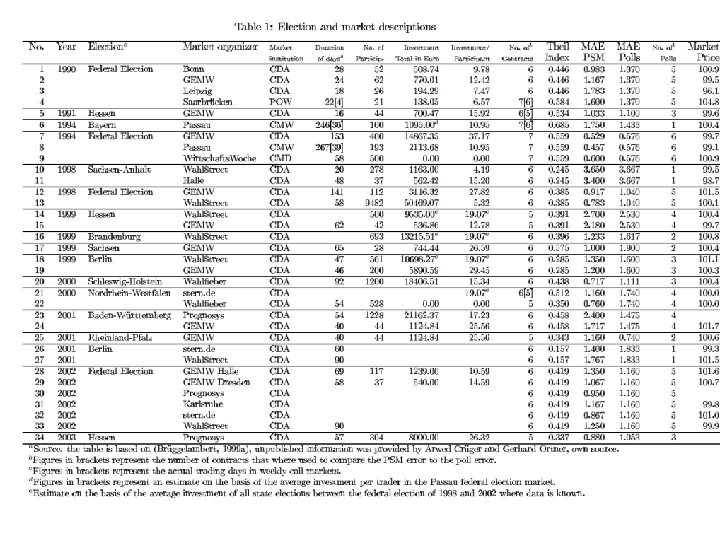
German data: contract level

Prediction error: contract level l Criterion – vi = true vote share of contract i – K = Number of different contracts
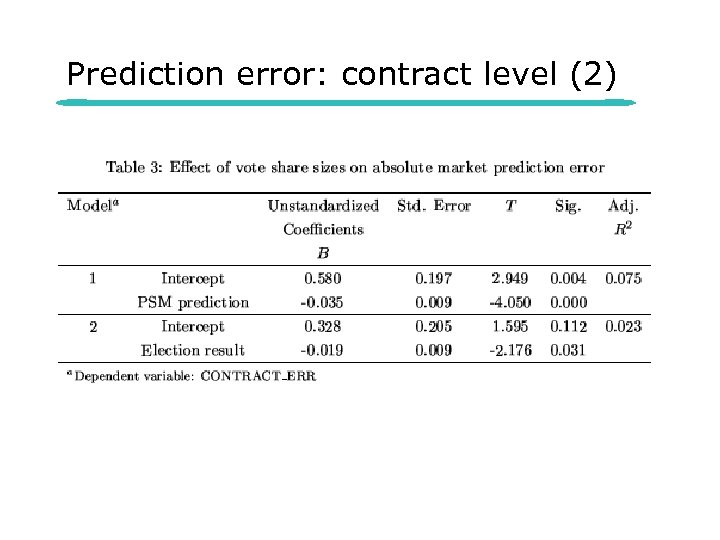
Prediction error: contract level (2)
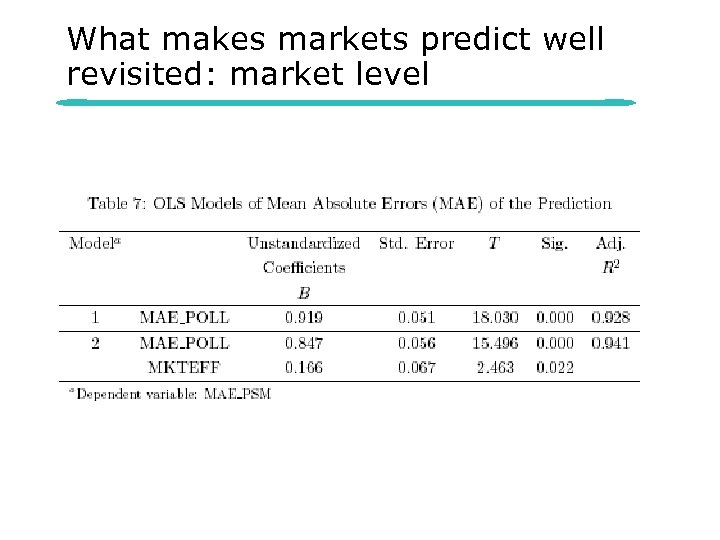
What makes markets predict well revisited: market level

Conclusions l We find overvaluation of small contracts, undervaluation of relatively large contracts in German PSM data – l Market level – – – l Bias not significant in US data (Forsythe et al. , 1999 JEBO) Market complexity in US data (Berg et al. , 1997) Market complexity constant in German data Electoral uncertainty and market efficiency Contract level: overconfidence bias – – – Jacobsen et al. (2000) EER Overvaluation of small contracts Disparity of different contracts (not significant)

Implications for PSM l l l PSM in Europe predict less successful than in he US because of the diversity of the vote shares and the complexity of the markets Polls in Europe predict more successful than in the US by correcting the raw data: the poll instrument is not biased by diversity of vote shares and the complexity of the markets Market design implications – – Minimizing number of contracts Correcting for the diverse vote share bias
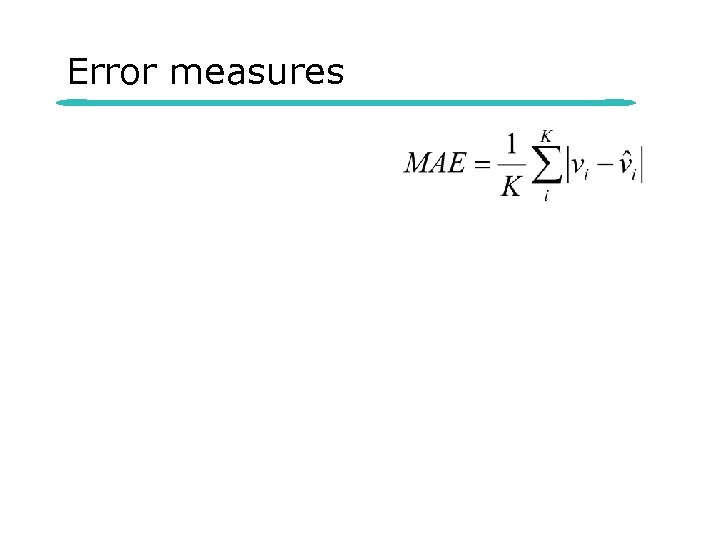
Error measures

Theory l l l Assumption: Trade is not driven by different preferences, but by individual information of the traders about the election result v(1 -v) is the unknown, true vote share of party P 1(P 2) Each trader receives a private signal si Є [v-ε, v+ε]

Theory (2) l l l l Definition p: = p 1=1 -p 2 Buy P 1 if market price p 1<si Buy P 2 if market price p 2<1 -si In equilibrium p is determined that the demand for both parties is equal Assumption: traders have the same endowment E Signal si<p buy E/p contracts P 1 Signal si>p buy E/(p-1) contracts P 2

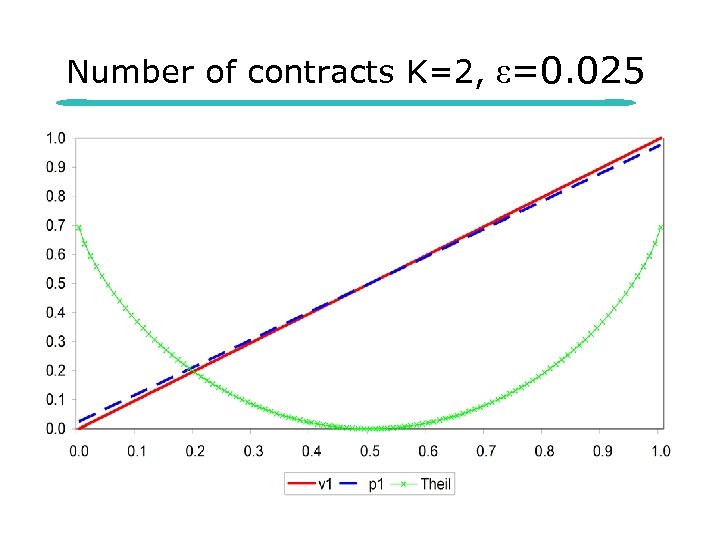
Predictions on contract level l p=(v+ ε)/(1+2ε) – Winner of the election v if – l v>1/2 that means p>1/2 Only if v 1=v 2=1/2 p is an unbiased estimator v 1=v>1/2 p 1=p<v=v 1, p 2=1 -p>1 v=v 2 – Large parties are undervalued, small parties are overvalued

Predictions l Market level – – l Mean absolute error (MAE) increases with ε Electoral uncertainty MAE increases when the vote shares become more unequal – diversity of the vote shares Contract level
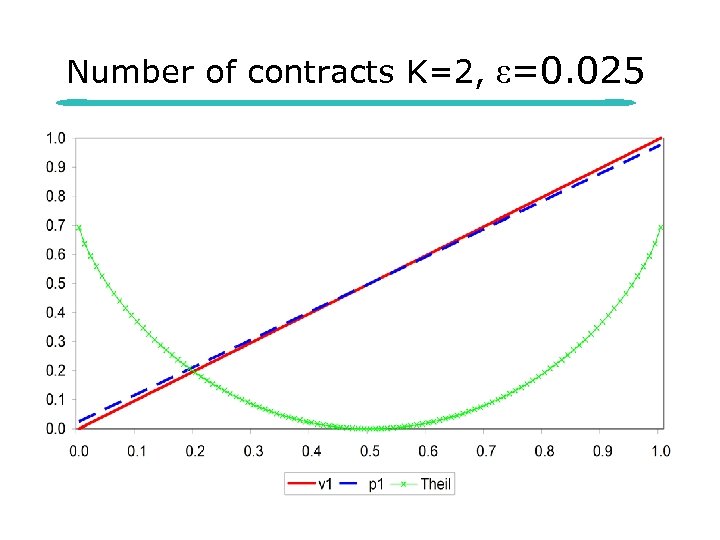
Number of contracts K=2, ε=0. 025

Measure for more than 2 contracts l l MAE increases when the vote shares become more unequal Captured for instance by a Theil coefficient
Number of contracts K=2, ε=0. 025
04a58ab51a7a439b7458628201b73e74.ppt