Arzamastsev_Computer_Simulation_2013.pptx
- Количество слайдов: 100

Overall budget February 2018 1

Математическое и компьютерное моделирование АРЗАМАСЦЕВ Александр Анатольевич February 2018 2

February 2018 3

February 2018 4

February 2018 5

February 2018 6

Математические модели описывают целый класс процессов или явлений, которые обладают сходными свойствами, или являются изоморфными. «Область знания становится наукой, когда она выражает свои законы в виде математических соотношений» Галилей, Пуанкаре February 2018 7

Владимир Иванович Вернадский (1863 -1945) «Большая часть научной работы заключается в поиске математических соотношений. Найдя их, наш ум успокаивается, и нам кажется, что вопрос, который нас мучил, решен. » February 2018 8

February 2018 9

Александр Андреевич Самарский – выдающийся российский математик, основоположник школы математического моделирования в России. Директор института математического моделирования РАН. Академик А. А. Самарский. 19 февраля 1919 года 11 февраля 2008 года. February 2018 На рубеже 70 -80 годов А. А. Самарский выступил с концепцией о методологии математического моделирования, как об «интеллектуальном ядре» процессов информатизации и познания. 10

Литература для самостоятельного изучения 1. Самарский А. А. , Михайлов А. П. Математическое моделирование. М. : Физматлит, 2002. - 320 с. (На кафедре компьютерного и математического моделирования имеется PDF файл этой книги). 2. Краснощеков П. С. , Петров А. А. Принципы построения моделей. М. : Изд-во МГУ, 1983. – 264 с. 3. Вабищевич П. Н. Численное моделирование. - М. : Изд-во МГУ, 1993. – 152 с. 4. Журнал «Математическое моделирование» . Издается Институтом математического моделирования РАН. (PDF – версии статей журнала представлены в Internet). 5. Арзамасцев А. А. Математическое и компьютерное моделирование. - Тамбов. ТГУ им. Г. Р. Державина, 2010. - 256 с. (На кафедре компьютерного и математического моделирования имеется PDF файл этой книги). February 2018 11
Содержание курса Лекции (24 ч. ) Лабораторные работы (24 ч. ) Самостоятельная работа (50 ч. ) Экзамен February 2018 12

Содержание курса (тематика лекций) Лекция #1. Математическая модель (ММ). Математическое моделирование. Основные понятия. Принципы математического моделирования. Области использования математических моделей. Лекция #2. Классификация математических моделей. Способы разработки ММ. Этапы построения ММ. Связь математического моделирования и других курсов. Ситуации, в которых математическое моделирование является единственным инструментом познания. Лекция #3. Пример разработки математической модели с помощью теоретического подхода. Математическая модель информационной системы и ее анализ. February 2018 13

Содержание курса (тематика лекций) Лекция #4. Пример разработки математической модели с помощью эмпирического подхода. Математическая модель способности индивидов к аппроксимационно-прогностической деятельности. Лекция #5. Пример разработки математической модели с помощью комбинированного подхода. Математическая модель термофлотационного разделения суспензий и ее анализ. Лекция #6. Пример разработки имитационной математической модели. Методы Монте-Карло. Клеточные автоматы. Модель роста популяции на плоскости и ее анализ. Лекция #7. Программные продукты, предназначенные для математического моделирования. Пакеты Mat. Lab, Simulink, Mach. CAD, Mapple, Mathematika, Statistika и др. Сравнение их возможностей. February 2018 14

Содержание курса (лабораторные работы) Лабораторная работа #1. Разработка генератора случайных чисел для стохастического имитационного моделирования Лабораторная работа #2. Проверка адекватности стохастической имитационной модели Лабораторная работа #3. Имитационное моделирование стохастического объекта Лабораторная работа #4. Разработка математической модели динамики Лабораторная работа #5. Параметрическая идентификация математической модели динамики Лабораторная работа #6. Построение фазовых портретов динамических систем на основе их математических моделей Лабораторная работа #7. Построение математической модели объекта с распределенными параметрами February 2018 15

Понятие математической модели Модель (model, simulator) – материальный объект, система математических зависимостей или программа, имитирующая структуру или функционирование исследуемого объекта (Першинов В. И. , Савинков В. М. Толковый словарь по информатике. - М. : Финансы и статистика, 1991). Моделирование, симуляция (simulation) – это имитация поведения некоторых существующих или предполагаемых систем или некоторых аспектов этого поведения (Толковый словарь по вычислительным системам / Под ред. В. Иллингуорта и др. - М. : Машиностроение 1990). Математическое моделирование (mathematical modeling) – метод исследования процессов и явлений на их математических моделях. Используется в тех случаях, когда эксперимент невозможен, затруднен или нецелесообразен (Першинов В. И. , Савинков В. М. Толковый словарь по информатике. - М. : Финансы и статистика, 1991). February 2018 16
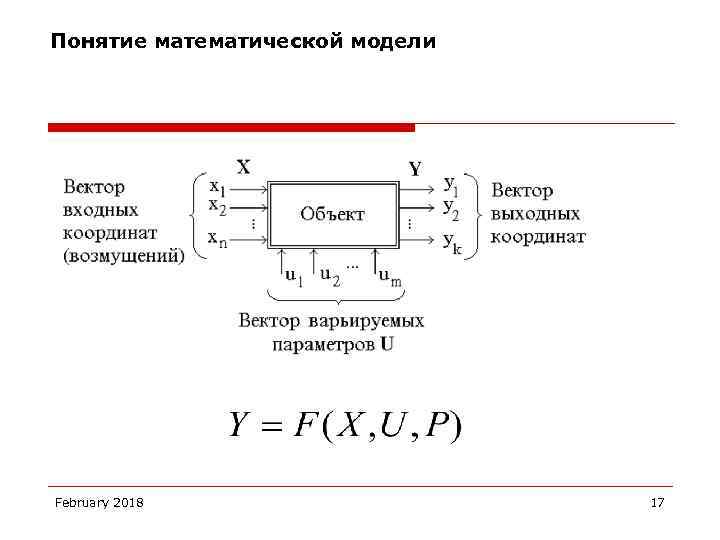
Понятие математической модели February 2018 17
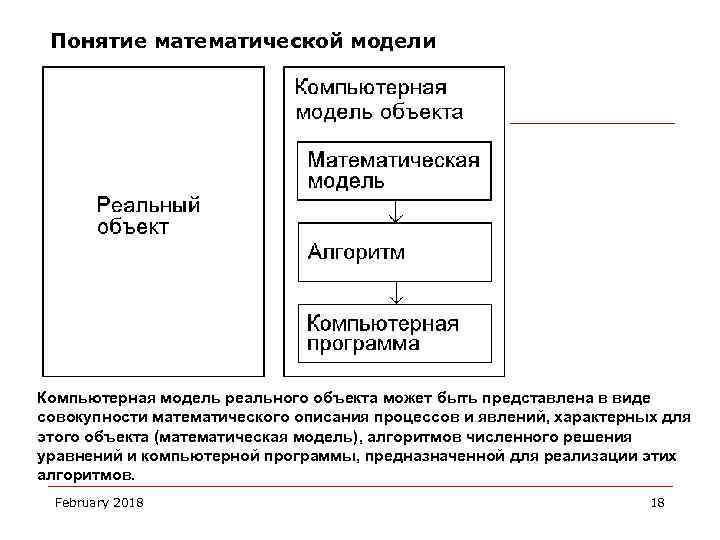
Понятие математической модели Компьютерная модель реального объекта может быть представлена в виде совокупности математического описания процессов и явлений, характерных для этого объекта (математическая модель), алгоритмов численного решения уравнений и компьютерной программы, предназначенной для реализации этих алгоритмов. February 2018 18
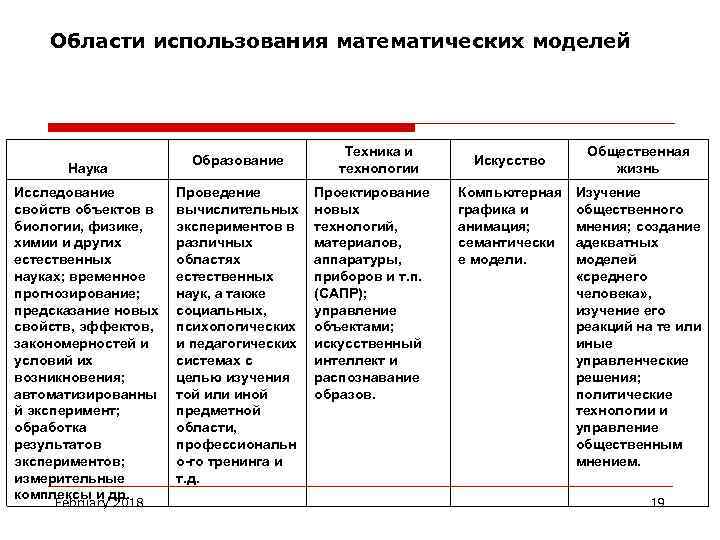
Области использования математических моделей Наука Исследование свойств объектов в биологии, физике, химии и других естественных науках; временное прогнозирование; предсказание новых свойств, эффектов, закономерностей и условий их возникновения; автоматизированны й эксперимент; обработка результатов экспериментов; измерительные комплексы и др. February 2018 Образование Проведение вычислительных экспериментов в различных областях естественных наук, а также социальных, психологических и педагогических системах с целью изучения той или иной предметной области, профессиональн о-го тренинга и т. д. Техника и технологии Проектирование новых технологий, материалов, аппаратуры, приборов и т. п. (САПР); управление объектами; искусственный интеллект и распознавание образов. Искусство Компьютерная графика и анимация; семантически е модели. Общественная жизнь Изучение общественного мнения; создание адекватных моделей «среднего человека» , изучение его реакций на те или иные управленческие решения; политические технологии и управление общественным мнением. 19

Принципы математического моделирования (Гультяев А. Визуальное моделирование в среде MATLAB. - СПб. : Питер, 2000) Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе ее моделирование лишено смысла. Поэтому существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена ее адекватная модель. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с заданной вероятностью и за конечное время. Обычно задают некоторое пороговое значение P 0 – вероятности достижения цели моделирования P(t), а также приемлемую границу t 0, времени достижения этой цели. Модель считают осуществимой, если может быть выполнено условие P(t 0) P 0. February 2018 20

Принципы математического моделирования Принцип множественности моделей. Данный принцип является ключевым. Речь идет о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного ее исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс. Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования. February 2018 21

Принципы математического моделирования Принцип параметризации. В ряде случаев моделируемая система имеет в своем составе некоторые относительно изолированные подсистемы, характеризующиеся определенным параметром, в том числе векторным. Такие подсистемы возможно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели. February 2018 22

Адекватность математической модели o Адекватность (adequacy) – соответствие, тождественность. o Адекватность моделирования (модели) – полнота и точность перевода информации с естественного языка на семантический. Зависит от возможностей семантического языка, разработанности правил перевода, точности соотнесения единиц двух языков (Першинов В. И. , Савинков В. М. Толковый словарь по информатике. М. : 1991). February 2018 23
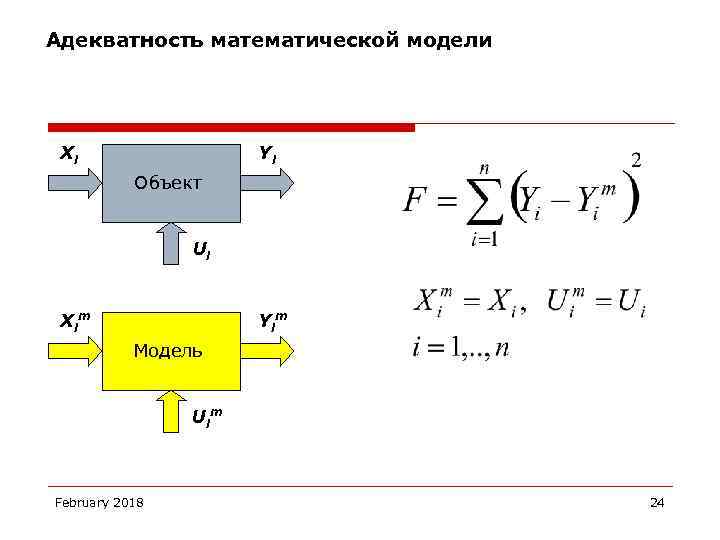
Адекватность математической модели Xi Yi Объект Ui Xim Yim Модель Uim February 2018 24
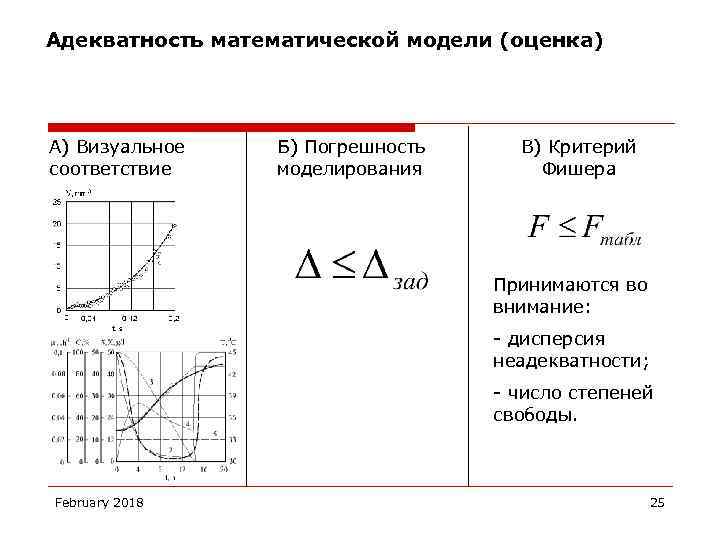
Адекватность математической модели (оценка) А) Визуальное соответствие Б) Погрешность моделирования В) Критерий Фишера Принимаются во внимание: - дисперсия неадекватности; - число степеней свободы. February 2018 25
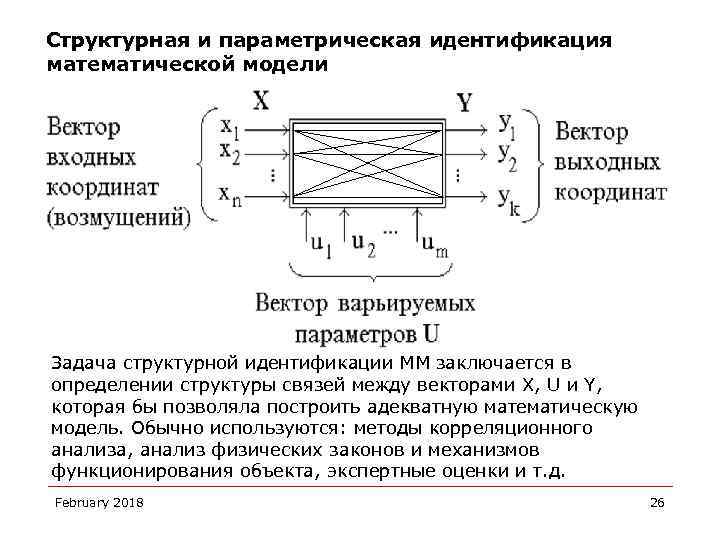
Структурная и параметрическая идентификация математической модели Задача структурной идентификации ММ заключается в определении структуры связей между векторами X, U и Y, которая бы позволяла построить адекватную математическую модель. Обычно используются: методы корреляционного анализа, анализ физических законов и механизмов функционирования объекта, экспертные оценки и т. д. February 2018 26
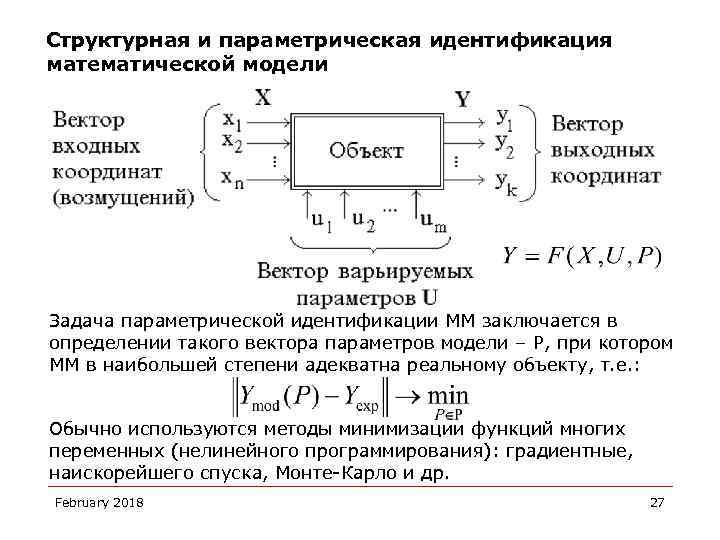
Структурная и параметрическая идентификация математической модели Задача параметрической идентификации ММ заключается в определении такого вектора параметров модели – P, при котором ММ в наибольшей степени адекватна реальному объекту, т. е. : Обычно используются методы минимизации функций многих переменных (нелинейного программирования): градиентные, наискорейшего спуска, Монте-Карло и др. February 2018 27

Классификация математических моделей 1. ММ статики и динамики 2. ММ детерминированные и стохастические 3. ММ с распределенными и сосредоточенными параметрами 4. ММ стационарные, нестационарные и квазистационарные 5. ММ непрерывные и дискретные February 2018 28

Математические модели динамики и статики А) Динамика February 2018 29
![Математические модели динамики и статики Б) Статика d[A]/dt = d[B]/dt = d[C]/dt = 0 Математические модели динамики и статики Б) Статика d[A]/dt = d[B]/dt = d[C]/dt = 0](https://present5.com/presentation/16236340_231197759/image-30.jpg)
Математические модели динамики и статики Б) Статика d[A]/dt = d[B]/dt = d[C]/dt = 0 February 2018 30
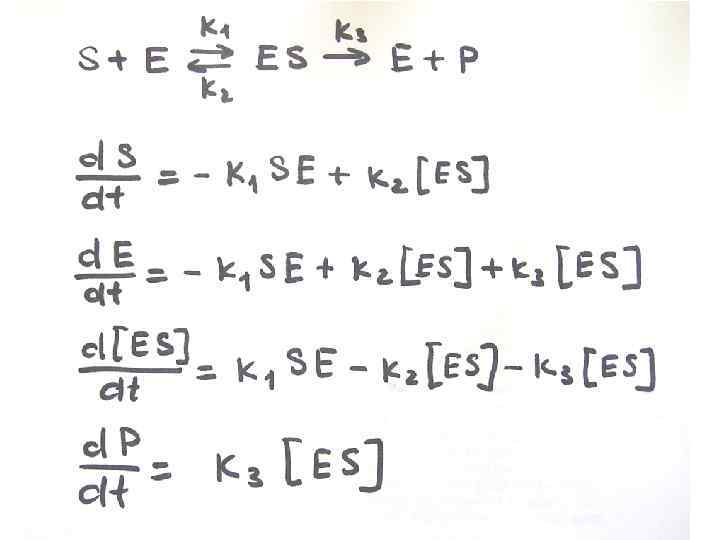
February 2018 31
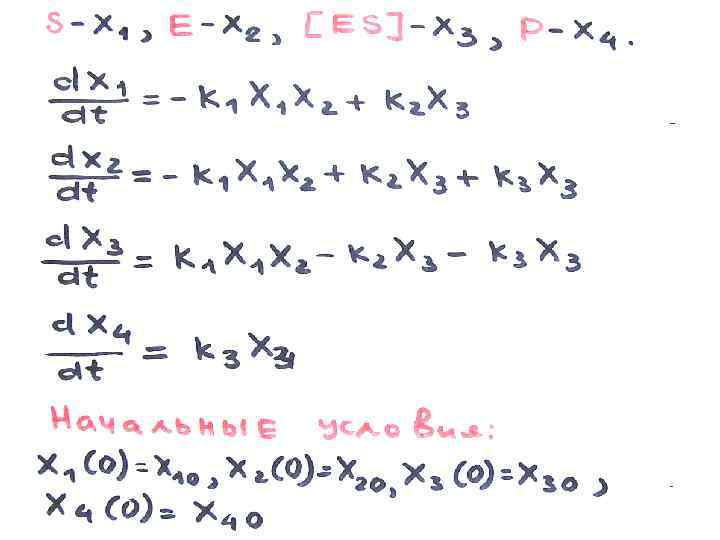
February 2018 32

February 2018 33
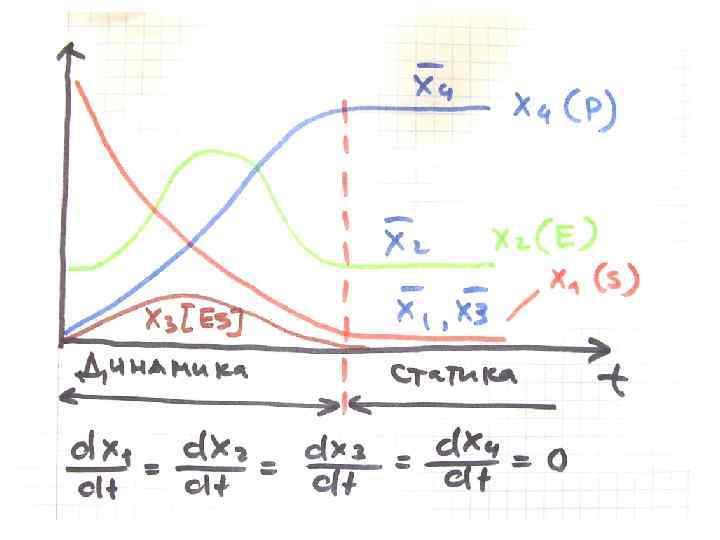
February 2018 34
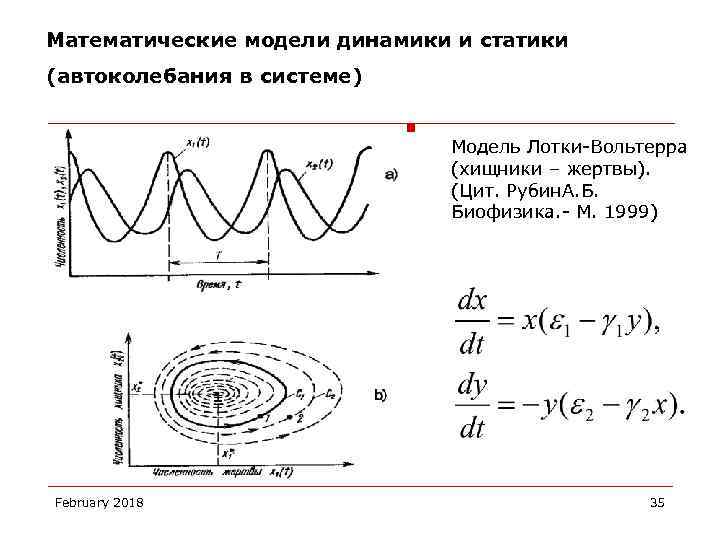
Математические модели динамики и статики (автоколебания в системе) Модель Лотки-Вольтерра (хищники – жертвы). (Цит. Рубин. А. Б. Биофизика. - М. 1999) February 2018 35

Математические модели динамики и статики (модель динамики для объекта с распределенными параметрами) February 2018 36
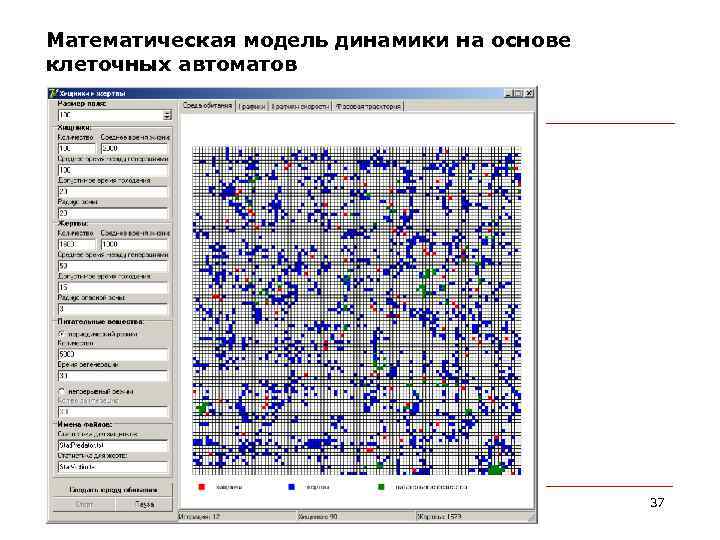
Математическая модель динамики на основе клеточных автоматов February 2018 37
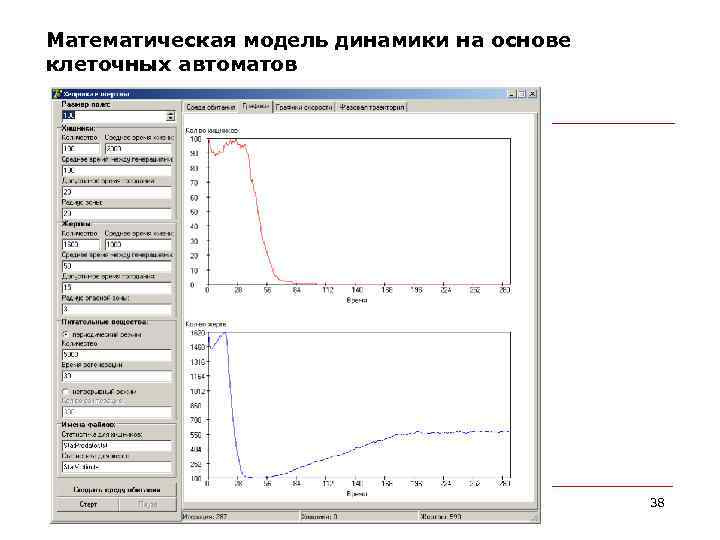
Математическая модель динамики на основе клеточных автоматов February 2018 38
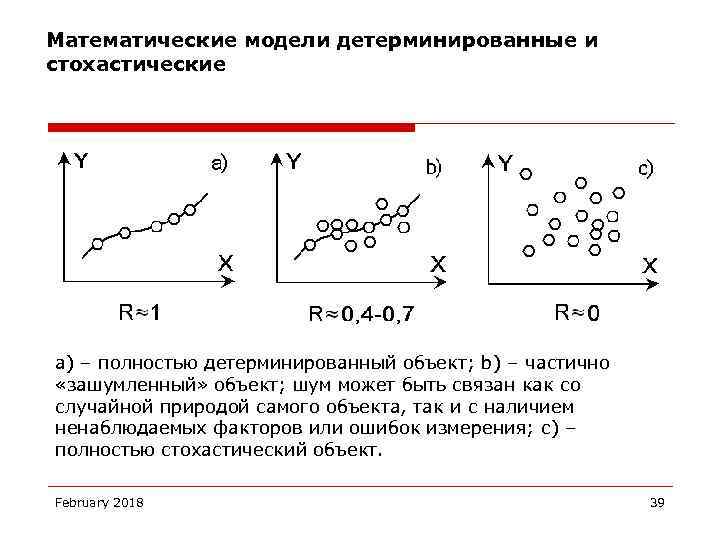
Математические модели детерминированные и стохастические a) – полностью детерминированный объект; b) – частично «зашумленный» объект; шум может быть связан как со случайной природой самого объекта, так и с наличием ненаблюдаемых факторов или ошибок измерения; c) – полностью стохастический объект. February 2018 39
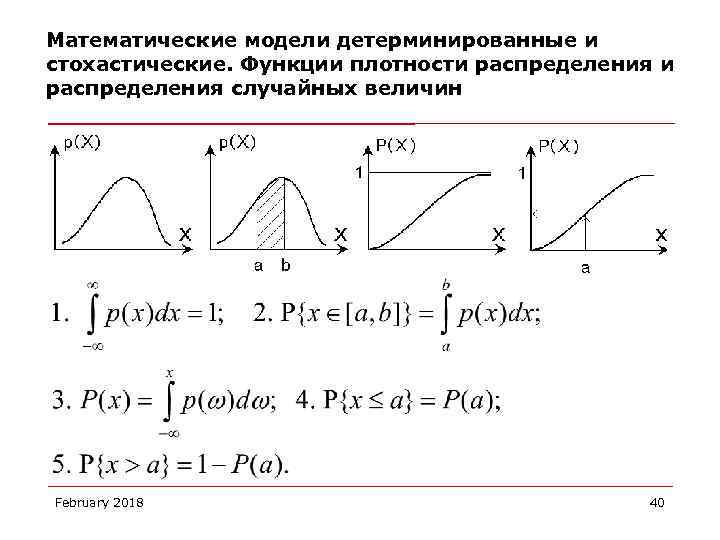
Математические модели детерминированные и стохастические. Функции плотности распределения случайных величин February 2018 40
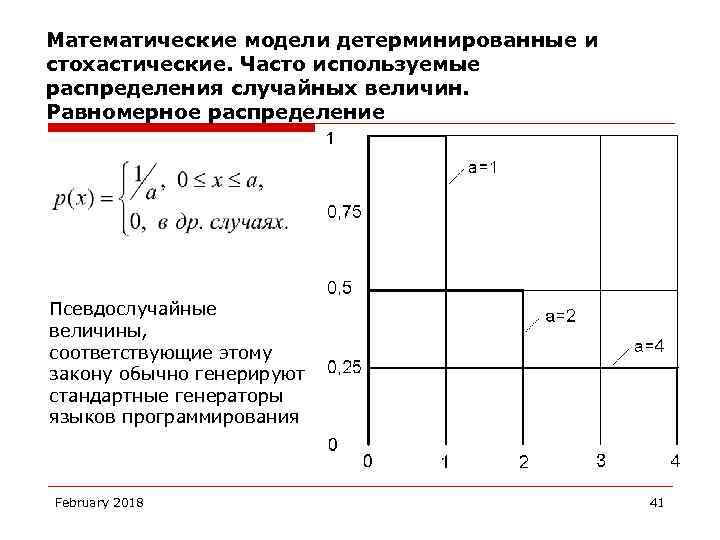
Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин. Равномерное распределение Псевдослучайные величины, соответствующие этому закону обычно генерируют стандартные генераторы языков программирования February 2018 41
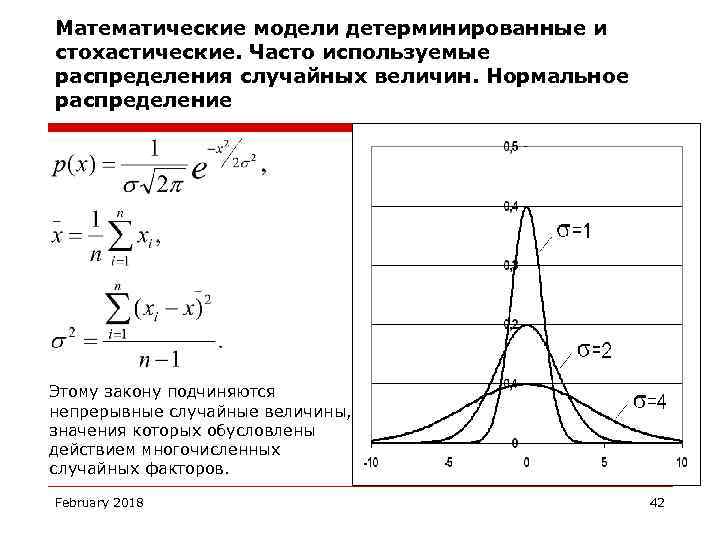
Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин. Нормальное распределение Этому закону подчиняются непрерывные случайные величины, значения которых обусловлены действием многочисленных случайных факторов. February 2018 42
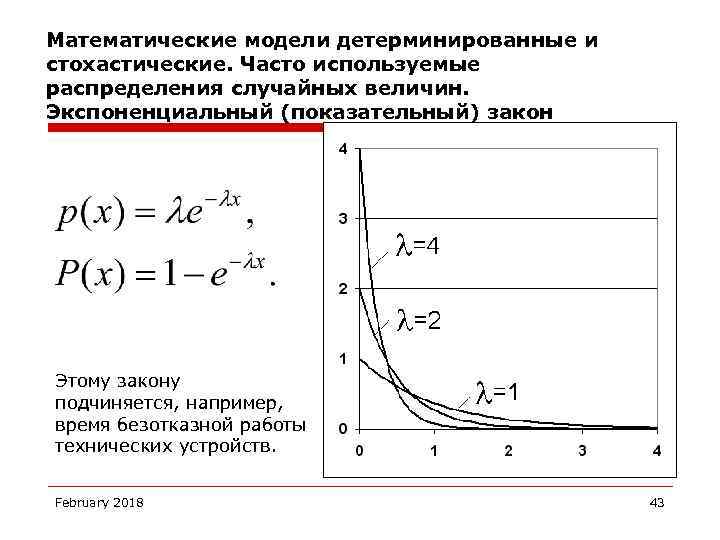
Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин. Экспоненциальный (показательный) закон Этому закону подчиняется, например, время безотказной работы технических устройств. February 2018 43

Где прочитать про генерирование случайных чисел на компьютере? Кнут Д. Э. Искусство программирования. М. , Спб. , Киев, 2001. Т. 2. (Получисленные алгоритмы). С. 19 -224. February 2018 44

Математические модели детерминированные и стохастические. Генерирование ста случайных (псевдослучайных) чисел на компьютере const N=100; { Количество случайных чисел } var f: text; i: integer; begin randomize; assign(f, 'data'); rewrite(f); for i: =1 to N do writeln(f, random(1000)/1000); close(f); end. February 2018 45
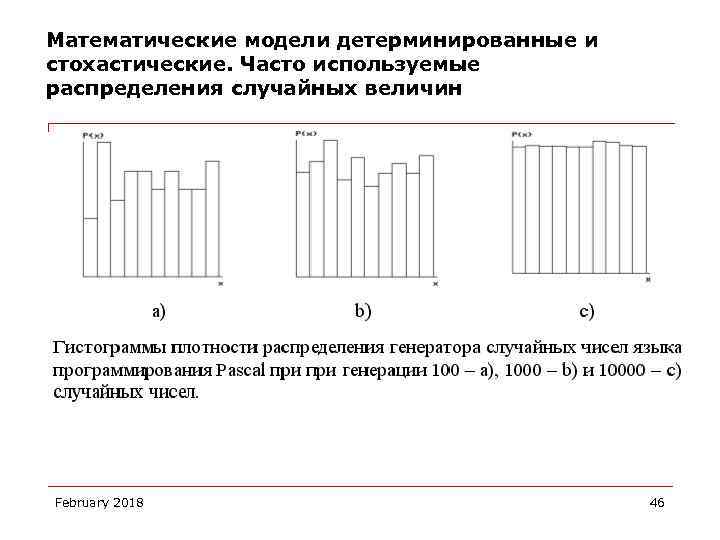
Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин const N=100; { Количество случайных чисел } var f: text; i: integer; begin randomize; assign(f, 'data'); rewrite(f); for i: =1 to N do writeln(f, random(1000)/1000); close(f); end. February 2018 46

Математические модели детерминированные и стохастические. Универсальный генератор случайных чисел {Программа генератора случайных чисел} uses crt; const N=5000; {Количество сгенерированных чисел } M=4; { Количество отрезков гистограммы } type mas=array[0. . M] of real; massiv=array[1. . N] of real; const x: mas =( 0, 10, 20, 30, 40 ); { Массив x } Pl: mas=(0, 0. 006667, 0. 03333, 0. 02, 0. 04 ); { Массив P(x) } var a: massiv; i: integer; f: text; File. Name: String[12]; Procedure Generator(N: Integer; P, X: mas; var A: massiv); type dim=array[1. . M] of integer; var l, i, j: integer; K: dim; poz 1, poz 2: integer; bufer: real; February 2018 47

Математические модели детерминированные и стохастические. Универсальный генератор случайных чисел { Определяем количества чисел, приходящихся на каждый из отрезков } begin for i: =1 to m do K[i]: =round(N*P[i]*(x[i]-x[i-1])); { Генерируем числа для каждого из отрезков } randomize; l: =1; for i: =1 to m do for j: =1 to K[i] do begin A[l]: =x[i-1]+random(10000)*(x[i]-x[i 1])/10000; l: =l+1 end; { Перемешиваем числа } for i: =1 to l do begin poz 1: =random(N-1)+1; poz 2: =random(N-1)+1; if poz 1<>poz 2 then begin February 2018 48
![Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин bufer: = A[poz 1]; Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин bufer: = A[poz 1];](https://present5.com/presentation/16236340_231197759/image-49.jpg)
Математические модели детерминированные и стохастические. Часто используемые распределения случайных величин bufer: = A[poz 1]; A[poz 1]: =A[poz 2]; A[poz 2]: =bufer end; begin { Начало программы } Generator(N, Pl, x, a); write('Имя файла для сгенерированных чисел -->'); readln(File. Name); assign(f, File. Name); rewrite(f); writeln('Сгенерированные числа: '); readln; for i: =1 to n do begin write(A[i]: 8: 3); writeln(f, A[i]) end; close(f) end. February 2018 49

Математические модели с сосредоточенными и распределенными параметрами (объект) Озеро, река, ванна с водой, участок воздушного бассейна, химический реактор (гидродинамика), живая клетка и т. д. February 2018 50
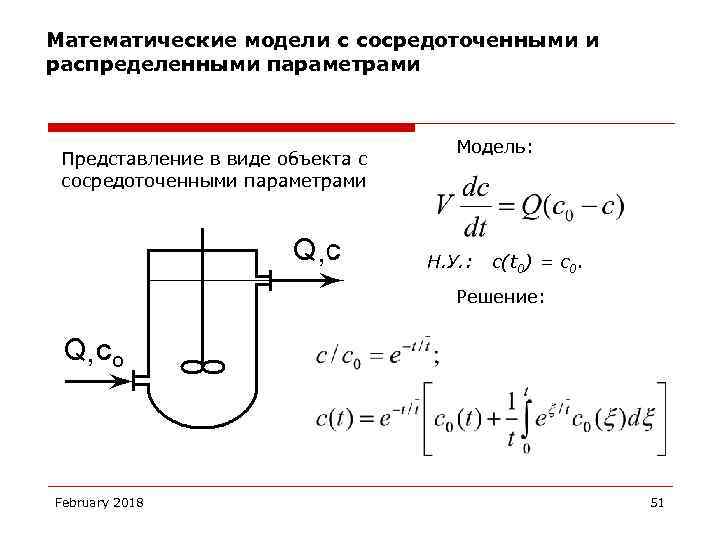
Математические модели с сосредоточенными и распределенными параметрами Представление в виде объекта с сосредоточенными параметрами Модель: Н. У. : c(t 0) = c 0. Решение: February 2018 51
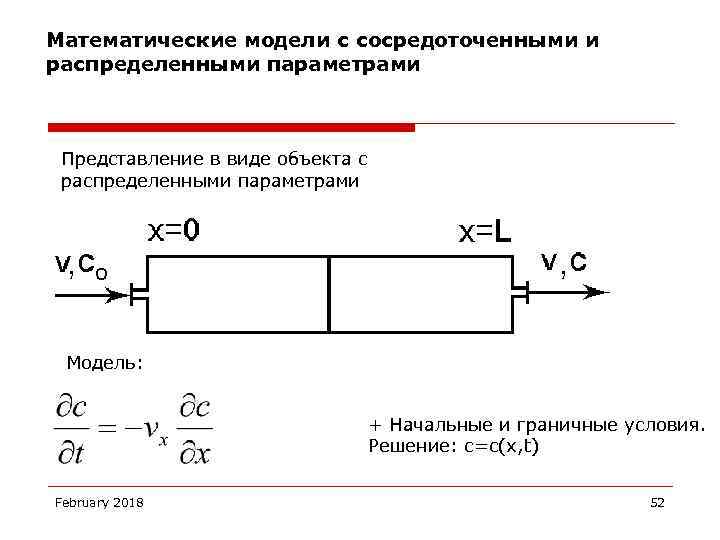
Математические модели с сосредоточенными и распределенными параметрами Представление в виде объекта с распределенными параметрами Модель: + Начальные и граничные условия. Решение: с=с(x, t) February 2018 52
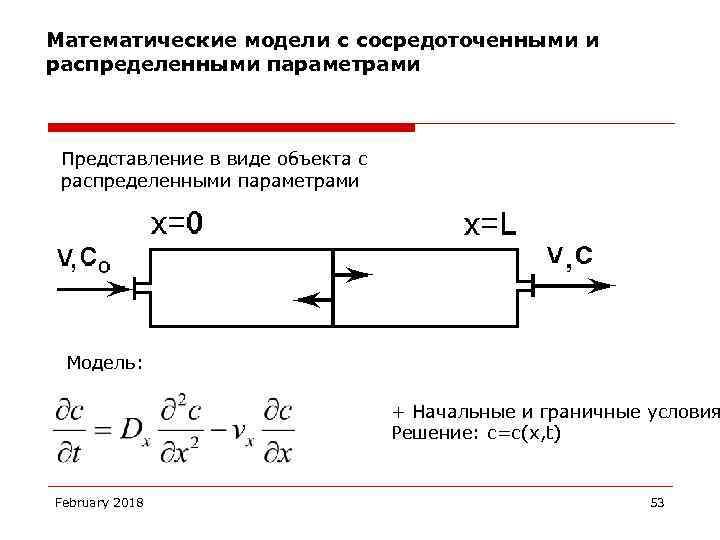
Математические модели с сосредоточенными и распределенными параметрами Представление в виде объекта с распределенными параметрами Модель: + Начальные и граничные условия Решение: с=с(x, t) February 2018 53
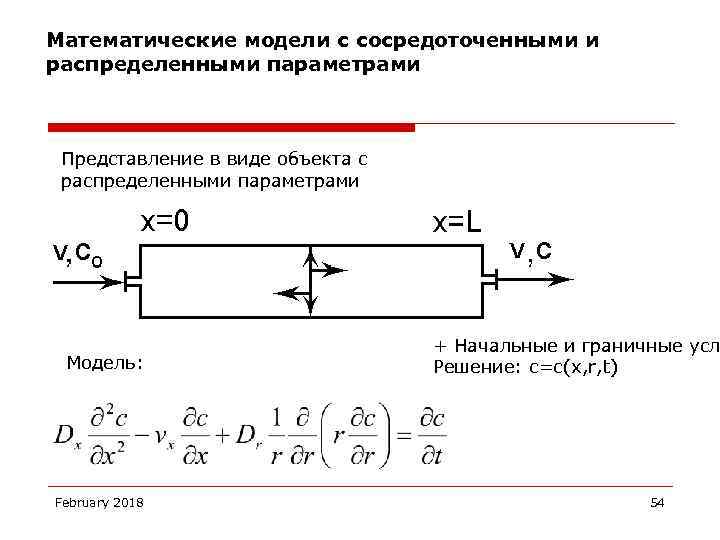
Математические модели с сосредоточенными и распределенными параметрами Представление в виде объекта с распределенными параметрами Модель: February 2018 + Начальные и граничные усл Решение: с=с(x, r, t) 54
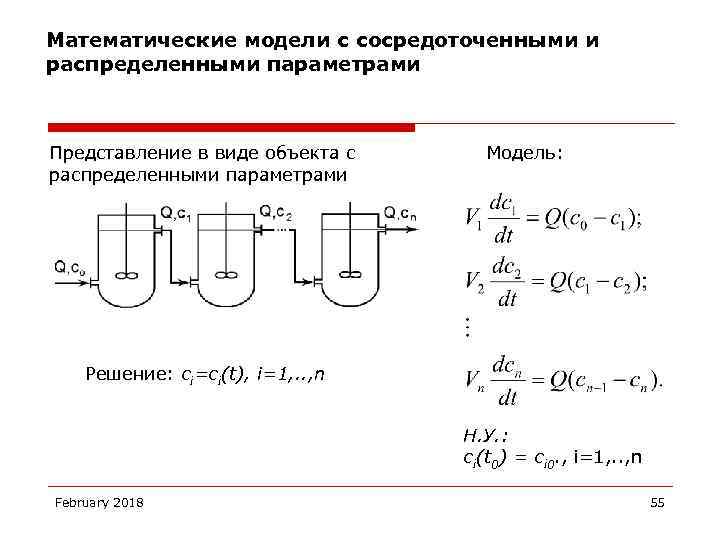
Математические модели с сосредоточенными и распределенными параметрами Представление в виде объекта с распределенными параметрами Модель: Решение: сi=сi(t), i=1, . . , n Н. У. : ci(t 0) = ci 0. , i=1, . . , n February 2018 55

Сравнение реакций различных математических моделей на стандартные воздействия February 2018 56

Математические модели непрерывные и дискретные Математические модели, которые получают обычно на основе законов сохранения, представляют собой дифференциальные уравнения – решения которых непрерывные функции. Т. е. обычно получают непрерывные математические модели Чем плохи непрерывные математические модели? 1. Во многих случаях они проявляют принципиальную неадекватность по отношению к моделируемому объекту. Например, графики изменения концентраций веществ February 2018 57
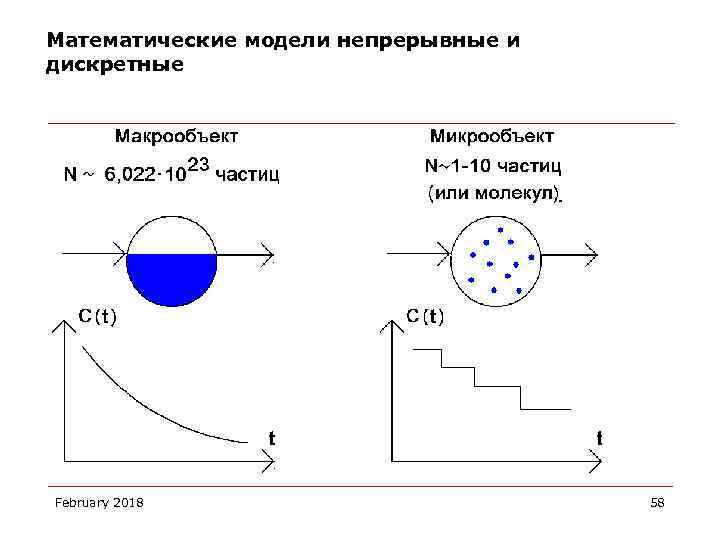
Математические модели непрерывные и дискретные February 2018 58

Математические модели непрерывные и дискретные 2. Необходимость численного моделирования. Как бы глубоки и разнообразны ни были методы качественного анализа математических моделей, область их применимости весьма ограничена. Это — либо простые, главным образом линейные, модели, либо отдельные фрагменты сложных, в том числе нелинейных моделей. Единственным универсальным способом исследования моделей является применение численных методов для нахождения приближенного решения поставленной задачи с помощью компьютера. Современные компьютеры являются дискретными. Т. е. при программировании любого алгоритма моделист получает дискретную модель. February 2018 59

Математические модели непрерывные и дискретные Конструирование дискретных вычислительных алгоритмов проходит в два этапа: -на первом строятся дискретные аналоги исходных моделей (например, записанных в форме обыкновенных дифференциальных уравнений или в дифференциальных уравнений в частных производных); -на втором дискрентные уравнения решаются численно. Пример 1. Пусть имеется следующая краевая задача: February 2018 60

Математические модели непрерывные и дискретные Заменим непрерывную область совокупность конечного числа точек N. на дискретную – Отрезок [0, ] поделим на равные части по правилу: February 2018 61

Математические модели непрерывные и дискретные Пример 2. Пусть имеется уравнение теплопроводности: February 2018 62
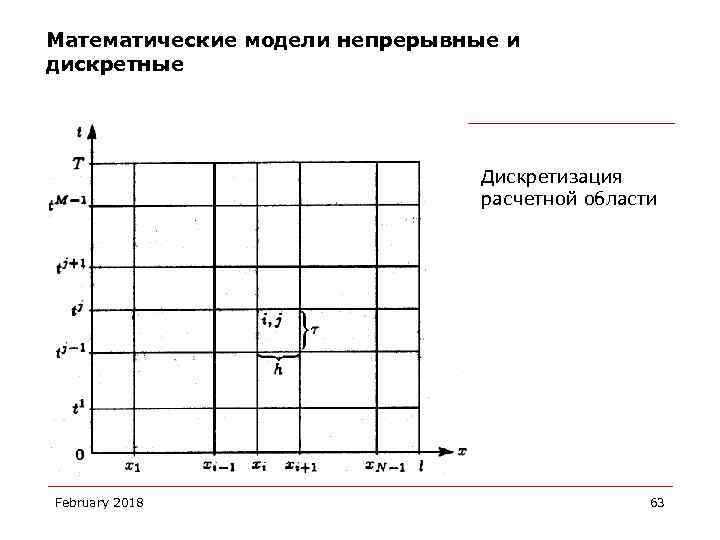
Математические модели непрерывные и дискретные Дискретизация расчетной области February 2018 63

Математические модели непрерывные и дискретные Дискретное представление задачи (4): February 2018 64
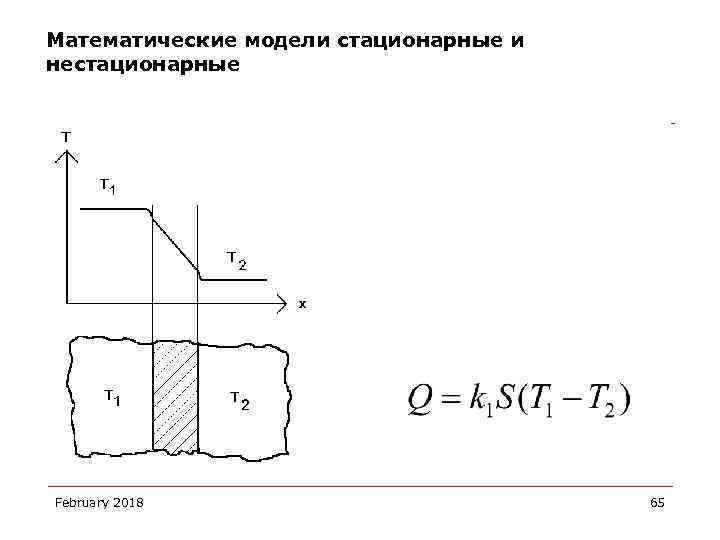
Математические модели стационарные и нестационарные February 2018 65
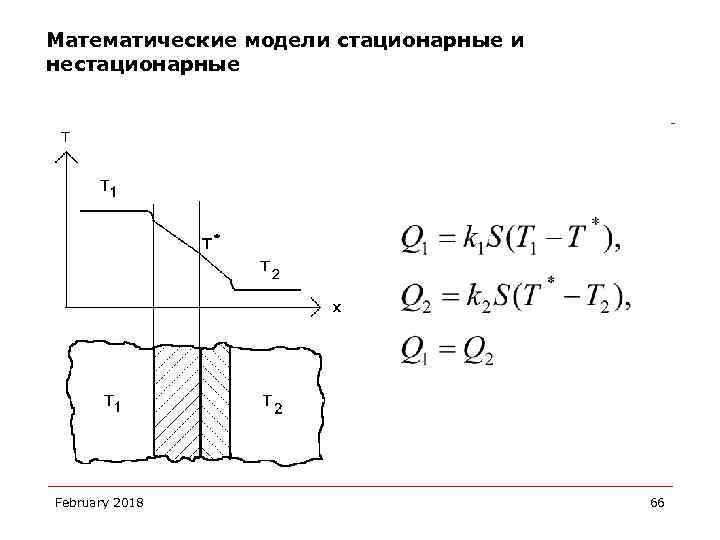
Математические модели стационарные и нестационарные February 2018 66
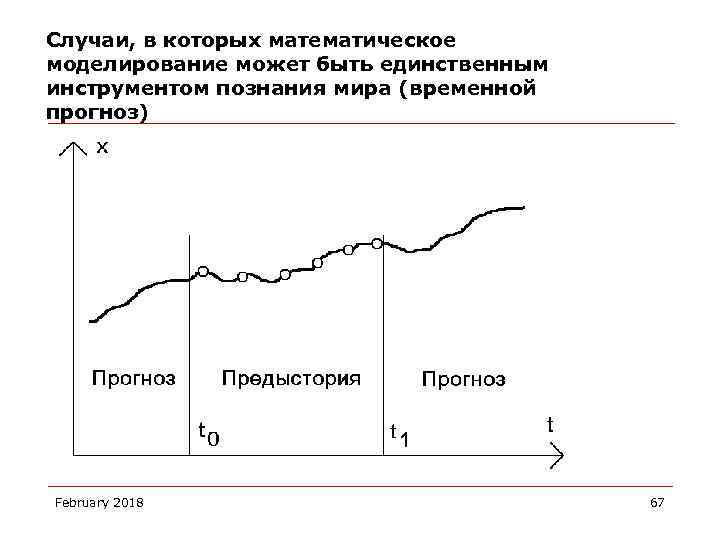
Случаи, в которых математическое моделирование может быть единственным инструментом познания мира (временной прогноз) February 2018 67
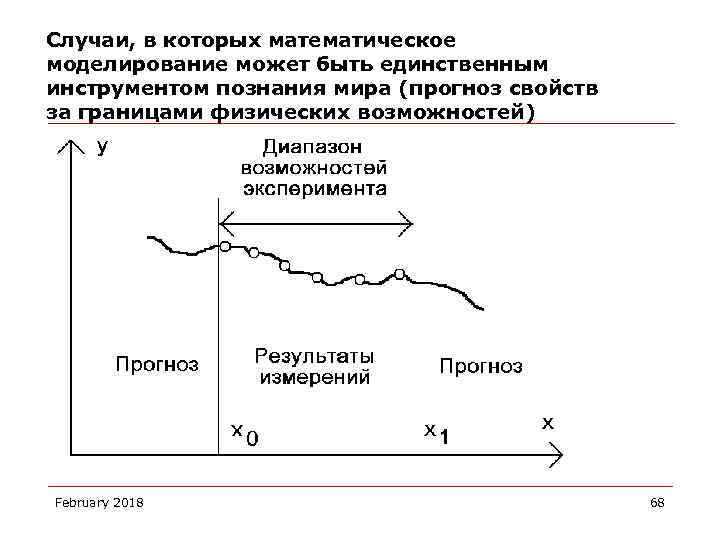
Случаи, в которых математическое моделирование может быть единственным инструментом познания мира (прогноз свойств за границами физических возможностей) February 2018 68

Случаи, в которых математическое моделирование может быть единственным инструментом познания мира Исследование свойств макрообъектов по свойствам микрообъектов (их составляющих) и правилам их взаимодействия. Прямая задача. Примеры: молекулярная динамика, Agent Based Approach, иерархические структуры Трудности: необходимы значительные вычислительные ресурсы February 2018 69

Случаи, в которых математическое моделирование может быть единственным инструментом познания мира Исследование свойств микрообъектов по свойствам макрообъектов и правилам взаимодействия микрообъектов; исследование правил взаимодействия микрообъектов по свойствам макро- и микрообъектов. Обратные задачи. Примеры: химическая и биохимическая кинетика, молекулярная динамика, Agent Based Approach, иерархические структуры. Трудности: не единственность решения и связанные с этим отбор решений, необходимы значительные вычислительные ресурсы. February 2018 70
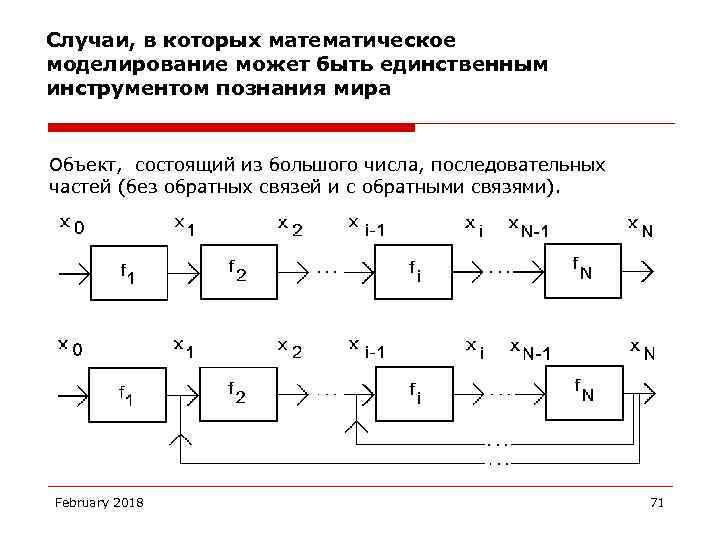
Случаи, в которых математическое моделирование может быть единственным инструментом познания мира Объект, состоящий из большого числа, последовательных частей (без обратных связей и с обратными связями). February 2018 71
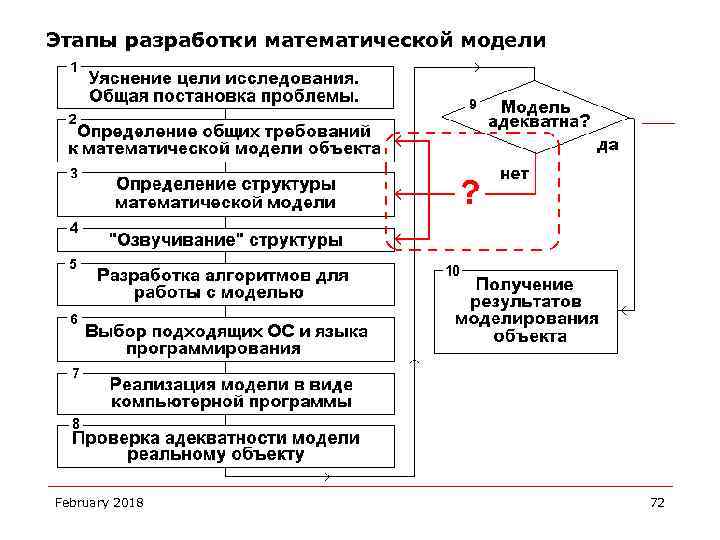
Этапы разработки математической модели February 2018 72

Какие законы и соображения могут быть положены в основу построения математической модели? А) Фундаментальные законы Природы; Б) Вариационные принципы; В) Иерархия объектов и свойства нижних уровней. February 2018 73
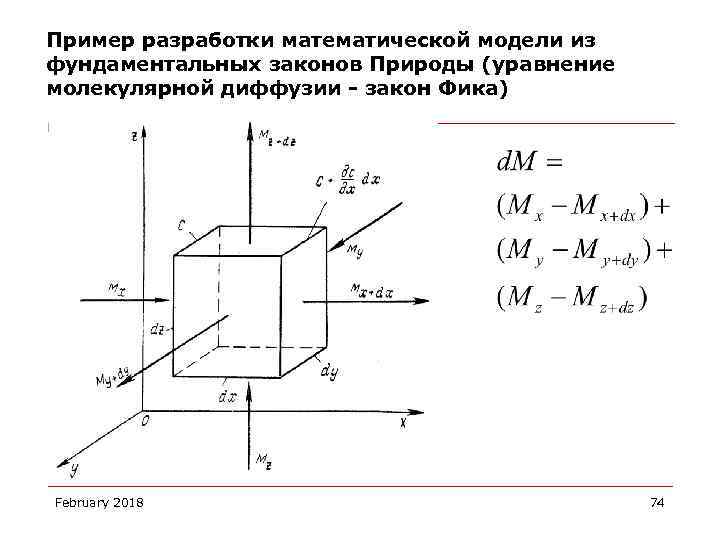
Пример разработки математической модели из фундаментальных законов Природы (уравнение молекулярной диффузии - закон Фика) February 2018 74

Пример разработки математической модели из фундаментальных законов Природы (уравнение молекулярной диффузии) February 2018 75

Пример разработки математической модели из фундаментальных законов Природы (уравнение молекулярной диффузии) Уравнение молекулярной диффузии: February 2018 76
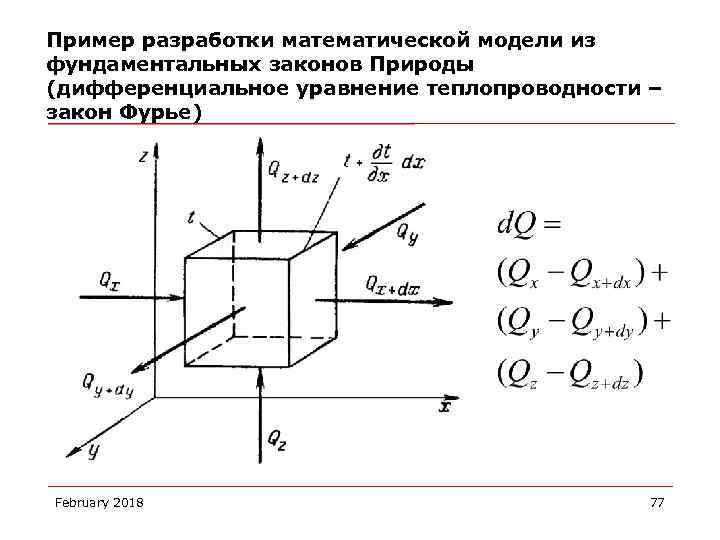
Пример разработки математической модели из фундаментальных законов Природы (дифференциальное уравнение теплопроводности – закон Фурье) February 2018 77

Пример разработки математической модели из фундаментальных законов Природы (дифференциальное уравнение теплопроводности – закон Фурье) February 2018 78

Пример разработки математической модели из фундаментальных законов Природы (дифференциальное уравнение теплопроводности – закон Фурье) Уравнение теплопроводности Фурье: February 2018 79

Граничные и начальные условия February 2018 80

Различные явления могут описываться одинаковыми математическими моделями А) Можно одно физическое явление моделировать (изучать) с помощью другого; Б) Можно использовать одинаковое программное обеспечение; В) Явления имеют подобные физические механизмы February 2018 81

Пример разработки математической модели из вариационных принципов «Многие законы Природы могут быть выведены из утверждения, что для истинного развития исследуемого процесса определенная характеристическая величина достигает минимального (в более общем случае экстремального) значения по сравнению с ее значениями для некоторых других возможных течений этого процесса. Чтобы математически сформулировать это утверждение, необходимо ввести в рассмотрение уравнения, описывающие данный процесс, и с помощью изменения (вариации) их формы добиться достижения экстремального значения вычисляемой характеристической величины. Те уравнения, при которых это экстремальное значение достигается, и выражают истинные законы изучаемого явления. В таком случае данное утверждение принимают за исходное и называют вариационным началом или вариационным принципом» . Трифонов Е. Д. (Евгений Дмитриевич) Соросовский образовательный журнал. № 6, 1998. С. 106 -111. February 2018 82
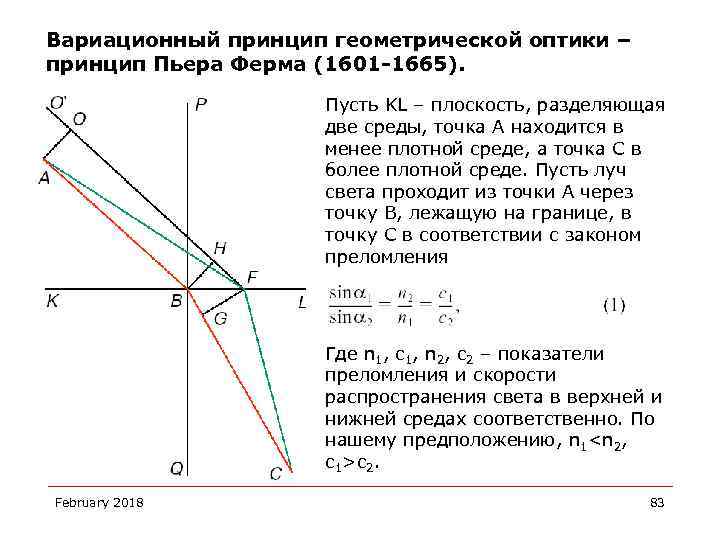
Вариационный принцип геометрической оптики – принцип Пьера Ферма (1601 -1665). Пусть KL – плоскость, разделяющая две среды, точка А находится в менее плотной среде, а точка С в более плотной среде. Пусть луч света проходит из точки А через точку В, лежащую на границе, в точку С в соответствии с законом преломления Где n 1, c 1, n 2, c 2 – показатели преломления и скорости распространения света в верхней и нижней средах соответственно. По нашему предположению, n 1<n 2, c 1>c 2. February 2018 83

Вариационный принцип геометрической оптики – принцип Пьера Ферма (1601 -1665). Требуется доказать, что время прохождения света по такому лучу самое короткое по сравнению с временем прохождения по любому другому преломленному лучу. Далее приведено доказательство от противного, сделанное Христианом Гюйгенсом (1629 -1695). Допустим, что свет прошел по другому лучу AFC, так что точка F отстоит от точки A дальше, чем точка B. Проведем прямую FO’, параллельную AB, и построим перпендикуляры AO и BH к этим прямым. Опустим также перпендикуляр FG на прямую BC. Угол HBF равен углу PBA, а угол BFG равен углу QBC, откуда следует, что: February 2018 84

Вариационный принцип геометрической оптики – принцип Пьера Ферма (1601 -1665). Поэтому, согласно (1), время распространения света по отрезку HF равно времени распространения по отрезку BG: Таким образом, время прохождения света по лучу OF равно времени прохождения света по пути ABG. Очевидно, что гипотенуза FC больше катета GC. Следовательно время прохождения по пути OFC больше, чем по пути ABC. Наконец, поскольку гипотенуза AF больше катета OF, то время прохождения света по пути AFC больше времени прохождения света по пути OFC и тем более по пути ABC! February 2018 85

Вопросы. 9 ноября 2007 года 1. О моделировании какого объекта шла речь на предыдущей лекции? 2. Дайте классификацию математических моделей, приведенных в предыдущей лекции, по пяти классификационным признакам. 3. Какие численные методы (известные вам из ранее изученных курсов) использовались при разработке указанных математических моделей? 4. Какие этапы в разработке данных математических моделей показались вам наиболее сложными и плохо формализованными? February 2018 86

Классификация математических моделей 1. ММ статики и динамики 2. ММ детерминированные и стохастические 3. ММ с распределенными и сосредоточенными параметрами 4. ММ стационарные, нестационарные и квазистационарные 5. ММ непрерывные и дискретные February 2018 87

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Академик Александр Андреевич Самарский – выдающийся российский математик, основоположник школы математического моделирования в России. Директор института математического моделирования РАН. o На рубеже 70 -80 годов Самарский. А. А. выступил с концепцией о методологии математического моделирования, как об «интеллектуальном ядре» процессов информатизации и познания. February 2018 19 февраля 1919 года 11 февраля 2008 года. 88

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o o Академик Виктор Вячеславович Кафаров — выдающийся ученый в области кибернетики химико-технологических процессов, автор 27 монографий, 9 справочников, 145 изобретений, более 2000 научных статей. Он участвовал в организации ряда всесоюзных совещаний и конференций: «Методы кибернетики химико-технологических процессов» , «Математическое моделирование сложных химико-технологических систем» . В. В. Кафаров подготовил около 300 кандидатов и 50 докторов наук, среди которых его ближайшие ученики и сподвижники — профессора В. В. Шестопалов, А. И. Бояринов, В. Л. Перов, И. Н. Дорохов, Л. С. Гордеев, В. Н. Ветохин, В. Н. Писаренко, В. П. Мешалкин, В. А. Иванов, Ю. А. Комиссаров, Д. П. Вент, В. В. Макаров, Д. А. Бобров, Н. В. Меньшутина, Э. М. Кольцова, А. И. Чулок, В. В. Меньшиков, А. Ф. Егоров, Т. Н. Гартман. February 2018 18 июня 1914 ? ? ? 89

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Профессор Балакирев Валентин Сергеевич, доктор технических наук. o Автор большого числа книг по математическому моделированию и теории управления. o Организатор ежегодной Всероссийской научной конференции «Математические методы в технике и технологиях» . February 2018 90

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o o Профессор Левин Виталий Ильич, доктор технических наук. Основные работы в областях: непрерывная логика; теория автоматов и моделирование сложных систем. Научные интересы: математические методы и информационные технологии в экономике, социологии и образовании, прикладная математическая логика, искусственный интеллект, интервальная математика, дискретная оптимизация в условиях неопределенности, теория автоматов, теория игр и решений. February 2018 91

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Academician, Prof. , Dr. Uldis Viesturs. o Scientific interests: simulation and optimal designing of bioreactors, process control, mixing in bioreactors, mass transfer in gas-liquid-solid systems. February 2018 92

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Профессор Мазалов В. В. , доктор физико-математических наук. o Директор института прикладных математических исследований Карельского научного центра РАН. o Научные интересы: теория игр, стохастическое динамическое программирование, математическая биология, теория вероятностей и математическая статистика, прикладная статистика February 2018 93

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Профессор Рудобашта Станислав Павлович, доктор технических наук. o Научные интересы: моделирование процессов тепломассопереноса, в т. ч. в системах с твердой фазой. February 2018 94

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Профессор Гордеев Лев Сергеевич, доктор технических наук. o Научные интересы: моделирование и оптимизация, системный анализ процессов и аппаратов химической технологии и биотехнологии, теоретические методы разработки математических моделей, алгоритмов и вычислительных программ, экспериментальные методы оценки адекватности математических моделей. February 2018 95

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Prof. , Dr. Klaus G. Troitzsch (University Koblenz-Landau, Germany). o Scientific interests: computer and mathematical simulation in social sphere, new means of computer simulation such as agent based approach. o Editor of Journal of Artificial Societies and Social Simulation February 2018 96

Ученые, внесшие значительный вклад в развитие математического и компьютерного моделирования o Prof. , Dr. Nigel Gilbert, University of Surrey (Great Britain). o Director of the University's Institute of Advanced Studies. o Scientific interests: computer and mathematical simulation in social sphere, new means of computer simulation such as agent based approach. o Editor of Journal of Artificial Societies and Social Simulation. February 2018 97

February 2018 98

Вопросы для мини коллоквиума 1. Адекватность математической модели. Постановка задач структурной и параметрической идентификации математической модели. 2. Разработка математических моделей на основе фундаментальных законов. 3. Этапы разработки математической модели объекта и их наполнение. February 2018 99

Overall budget February 2018 100
Arzamastsev_Computer_Simulation_2013.pptx