OUTLINES Outline 1 PDE toolbox DEMOS 2 Reference

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

PDE DEMOS >> pdedemos C: Program FilesMATLABR 2008 btoolboxpde

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

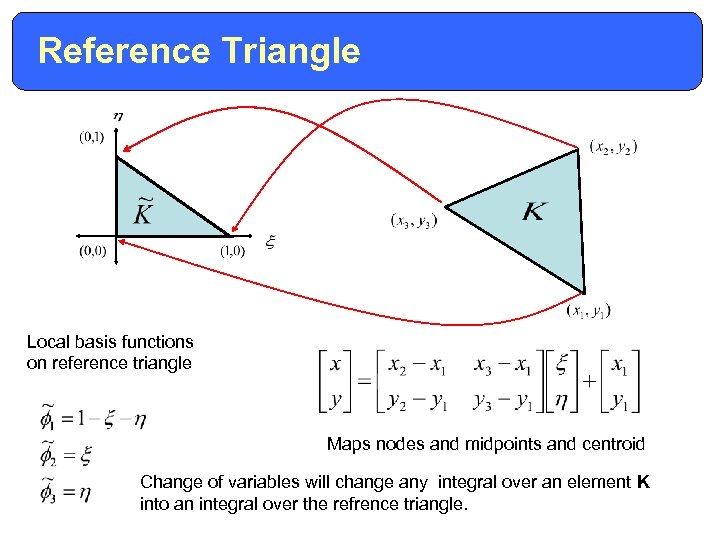
Reference Triangle Local basis functions on reference triangle Maps nodes and midpoints and centroid Change of variables will change any integral over an element K into an integral over the refrence triangle.

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

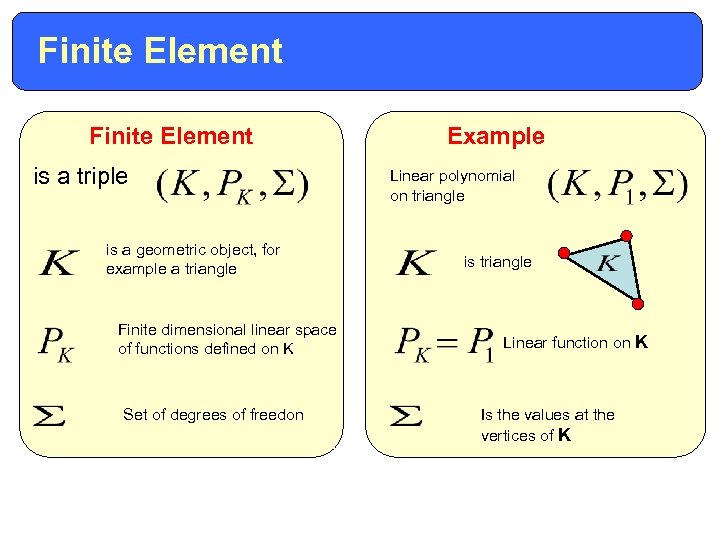
Finite Element is a triple is a geometric object, for example a triangle Finite dimensional linear space of functions defined on K Set of degrees of freedon Example Linear polynomial on triangle is triangle Linear function on K Is the values at the vertices of K

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

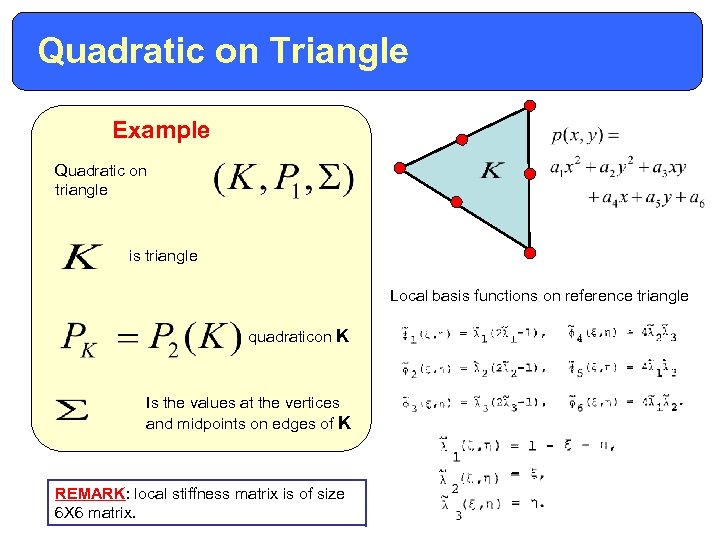
Quadratic on Triangle Example Quadratic on triangle is triangle Local basis functions on reference triangle quadraticon K Is the values at the vertices and midpoints on edges of K REMARK: local stiffness matrix is of size 6 X 6 matrix.

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

bilinear on rectangle Example bilinear on rectangle Is a rectangle Local basis functions on reference rectangle Bilinear on K Is the values at the vertices of the rectangle K REMARK: local stiffness matrix is of size 4 X 4 matrix.

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

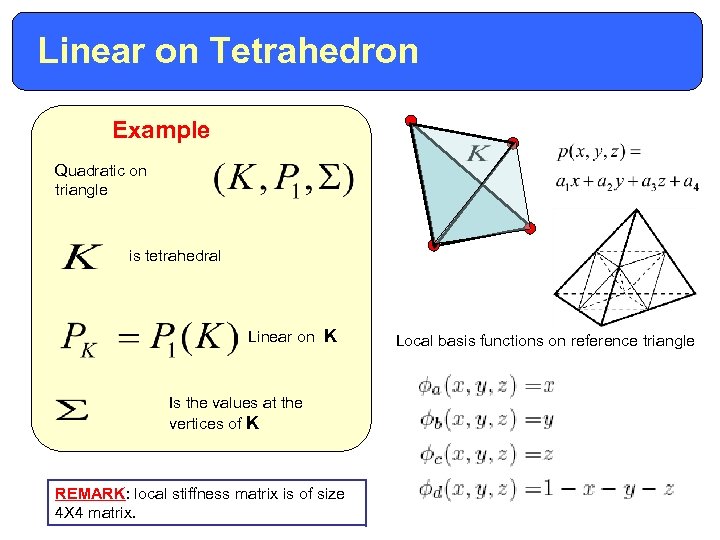
Linear on Tetrahedron Example Quadratic on triangle is tetrahedral Linear on K Is the values at the vertices of K REMARK: local stiffness matrix is of size 4 X 4 matrix. Local basis functions on reference triangle

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

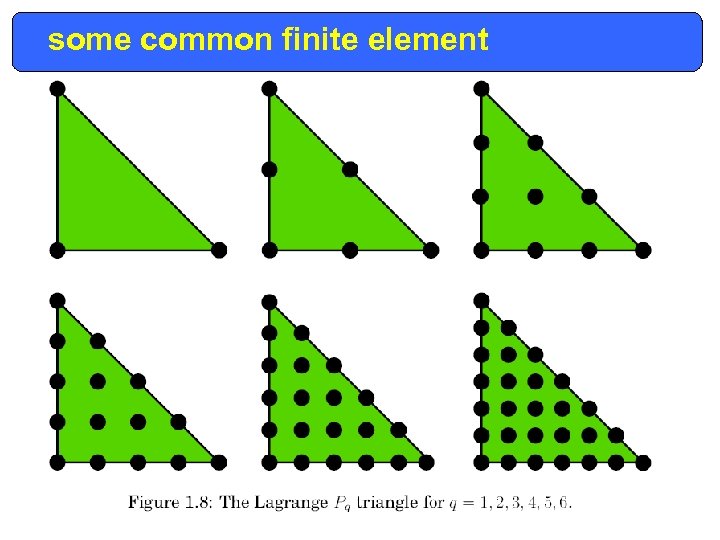
some common finite element

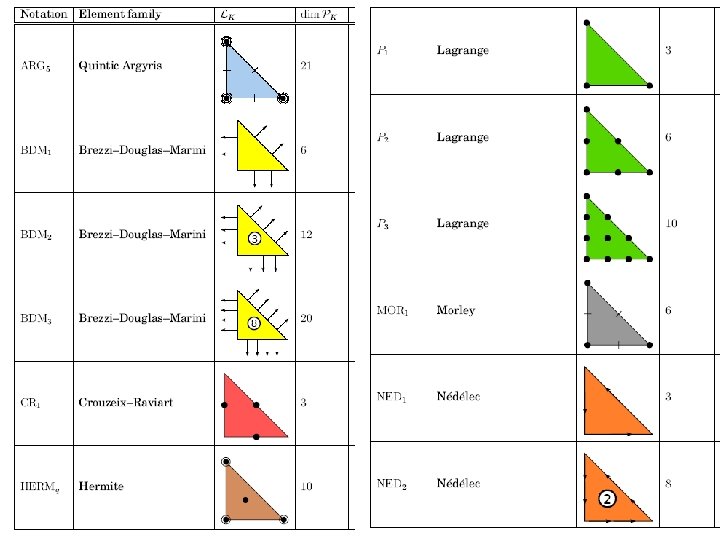
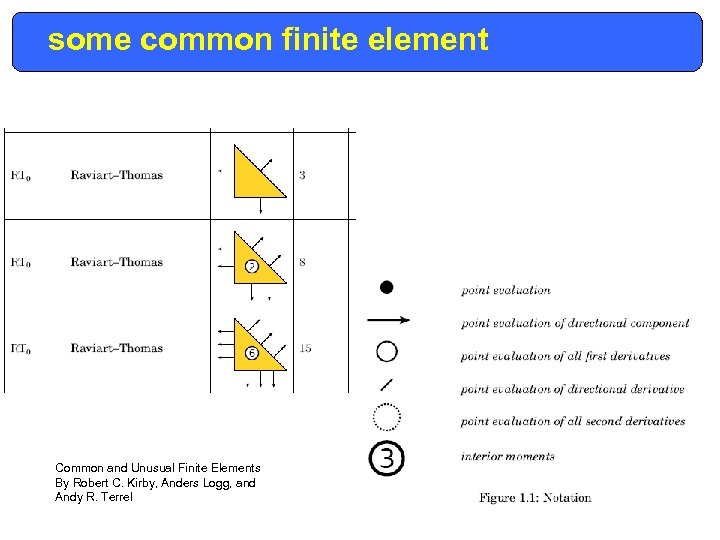
some common finite element Common and Unusual Finite Elements By Robert C. Kirby, Anders Logg, and Andy R. Terrel

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

delaunay 3 How many elements? x = [-1 -1 1 1 0]; y = [-1 -1 1 1 0]; z = [-1 1 0]; T = delaunay 3( x, y, z, {'Qt', 'Qbb', 'Qc', 'Qz'} ); XX = [x(: ), y(: ), z(: )]; tetramesh(T, XX); d = [-1 1]; [x, y, z] = meshgrid(d, d, d); % A cube x = [x(: ); 0]; y = [y(: ); 0]; z = [z(: ); 0]; % [x, y, z] are corners of a cube plus the center. Tes = delaunay 3(x, y, z); XX = [x(: ), y(: ), z(: )]; tetramesh(Tes, XX); 3 d. zip

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

Line Command (PDETOOL) g=[ 2 2; -1 1 1 -1; % g='squareg'; -1 1; % The [-1, 1]x[-1, 1] square -1 1 1 -1; 1 1; 0 0 ]; % pde coeff c=1; a=0; f = '-2*((x. ^2 - 1) + (y. ^2 - 1))'; % right hand side % Mesh [p, e, t]=initmesh(g, 'Hmax', 0. 1); pdemesh(p, e, t) % Solve [A, rhs, B, ud] = assempde(b, p, e, t, c, a, f); [u 1] = pcg(A, rhs, 1 e-5, 100); %u 1=Arhs; uh = B*u 1+ud; %uh = assempde(b, p, e, t, c, a, f); % visualize x=linspace(-1, 1, 31); y=x; [uu]=tri 2 grid(p, t, uh, x, y); Figure; surf(x, y, uu); u=0 b=[ 1 1 ; 1 1 1 1; 1 1 ; % b='squareb 1'; 1 1 ; % Dirichlet data 1 1; '0' '0'; '1' '1'; ‘ 0' '0' '0‘ ]; Sample. zip

Line Command (PDETOOL) For each column in the Decomposed Geometry matrix there must be a corresponding column in the Boundary Condition matrix. The format of each column is according to the following list: u=0 b=[ 1 1 ; 1 1 1 1; 1 1 ; % b='squareb 1'; 1 1 ; % Dirichlet data 1 1; '0' '0'; '1' '1'; ‘ 0' '0' '0‘ ];

OUTLINES Outline: 1) PDE toolbox DEMOS 2) Reference Triangle 3) Finite Element triple 4) Quadratic on Triangle 5) Bilinear on Rectangle 6) Linear on Tetrahedron 7) some common finite element 8) delaunay 3 Matlab command 9) Line Command (PDETOOL) 10) Resources: (videos, Books, Workshop, Conf)

Resources http: //www. mathworks. com/access/helpdesk/help/pdf_doc/pde. pdf

Resources http: //ocw. mit. edu/courses/mathematics/18 -085 -computational-scienceand-engineering-i-fall-2008/video-lectures/lecture-18 -finite-elements-in 1 d-part-2/ Gilbert Strang Videos (MIT Open. Course. Ware)

Resources

Resources Adina R&D, Inc. Algor (Professional) Alstom (SLIM) Altair AMPS Amtec (Mesh Generator) Anker-Zemer (LINFLOW) Ansoft Corporation (HFSS) ANSYS ATIR (STRAP) Argus Interware, Inc. (Argus ONE) Auto. FEA Software Co. (JL Analyzer) Automated Analysis Corporation (COMET) CAE Power. Tools CADFEM CAST 3 M CEETRON (GLview) CIMNE (Gi. D) Civil. FEM Cobus (Fesa. Win) Computational Mechanics Co. (Pro. PHLEX) Computational Mechanics Australia (Meshing) Computers and Structures Inc. COMSOL (FEMLAB) COMSOL (PDE Toolbox) Computing Objects (CM 2) Concurrent Analysis Corporation (CAEFEM) Cross. X Cyberlogic (FEMdesigner) DIANA D. I. E Software Dr. Software EDS (FEMAP) EDS PLM Solutions (I-DEAS Simulation) Electric Power Research Institute (Merlin, Spider) Engineering Mechanics Research Corporation ESI Group (PAM-SYSTEM) Fastflo ESRD (Stress. Check) FEA Ltd. (LUSAS) FEMCOS (COSAR) Femsys (FEMGV) Field Precision (Tri. Comp/AMaze/Gam. Bet) Finit. ES-Plast Flexcom-3 D (MCS) FLUENT (FLUENT/FIDAP) For. Dyn animation Frame. Master GEO-SLOPE Hibbitt, Karlsson and Sorensen (ABAQUS) HOMARD ICEM CFD Engineering Integrated Design and Analysis Consultants (IDAC) Inter-CAD Ltd (Axis. VM) Intuition Software (Visual. FEA) INFOLYTICA Intelligent Light (Field. View) Intes (PERMAS) Laboratoire Central des Ponts et Chaussees (CESAR) Lawrence Livermore National Laboratory (DYNA 3 D/NIKE 3 D) LEAP (ANSYS) LIRA Finite Element Analysis Software LISA Livermore Software Technology Corp. (LS-DYNA 3 D) Mac. Neal-Schwendler Corporation (MSC/NASTRAN, MSC/PATRAN) MACRO Industries (MI/NASTRAN) SAGE CRISP Macsyma (PDEase) SAMTECH (samcef) Magsoft (ATILA, Flux 2 D) SDTools (Structural Dynamics Toolbox) Makros-A SEPRA (SEPRAN) Maple SIMULOG (Tet. Mesh-GHS 3 D) MARC Softing (Nolian) Mathematica Softek Services Ltd. (P-FRAME, S-FRAME) Mathworks (MATLAB) Soilvision (SVFlux) Mathworks (Simulink) SOLVIA MIDAS SRT (FEA-Crack) MSTR Technology (FEWaves) Steer Engineering (AFEMS, Fem. Form, Fem. Tool) NM SESES (Centre for Computational Physics ZHW) Strand 7 Noran Engineering, Inc. (NEi. Nastran) Structural Analysis Inc (m. TAB*STRESS) Northwest Numerics and Modelling (Zebulon) Structural Research & Analysis Corp (COSMOS/M) Numerical Objects (Diffpack) GT STRUDL Open Engineering (Oofelie) Synaps (Epogy) PDE 2 D T-Systems (MEDINA) PDE Solutions Inc (Flex. PDE) Tera Analysis (Quick. Field) Parametric Technology Corporation (Pro/MECHANICA) Thermo. Analytics (Rad. Therm) PLAXIS Thin-Walled Structures Software Pointwise, Inc (Gridgen/FIELDVIEW) Third Wave Systems (Advant. Edge) PVM Corp (FEVA) True. Grid PVM Corp (SAGE) Utah State University (VABS) Radioss Consulting Corp. Vector Fields (TOSCA, OPERA) Research Engineers (STAAD) Vector. Space Programming (vs. lib) Robobat (Robot 97) Visual Kinematics Inc. (Dev. Tools) Rockfield (ELFEN) Visual Numerics (PV-WAVE) Roensch & Associates VMA Engineering (GENESIS) Weidlinger Associates Inc. ZACE Services Ltd. Zentech International (Zencrack)

Resources