lek_5.ppt
- Количество слайдов: 32

Открытые резонаторы

Почему необходимо перейти к открытому резонатору? • При переходе от радиодиапазона СВЧ к оптическому диапазону добротность резонатора (замкнутой полости) падает. Это объясняется тем, что добротность замкнутой металлической полости определяется отношением линейного размера к глубине проникновения излучения в металле • При нормальном скин эффекте глубина проникновения поля в металл • размер полости должен быть соизмерим с длиной волны • Поэтому добротность с ростом частоты падает

• Можно было бы увеличить линейный размер полости, но возникает другая проблема. • с увеличением частоты возрастает число мод резонатора , а частотный интервал, приходящийся на одну моду, падает: • С другой стороны, ширина резонансной кривой соответствующего колебания для фиксированного объема возрастает • Поэтому резонансные кривые соседних мод перекрываются и резонатор теряет свои резонансные свойства. •

• Первые открытые резонаторы в виде двух плоских параллельных зеркал (резонатор Фабри Перо) предложили в 1958 А. М. Прохоров, а затем американские учёные Р. Х. Дикке, А. Л. Шавлов и Ч. Таунс. • Под открытым резонатором понимают некоторую колебательную систему, образованную совокупностью зеркал, в которой могут возбуждаться и поддерживаться слабо затухающие электромагнитные колебания оптических и СВЧ диапазонов с излучением в свободное пространство
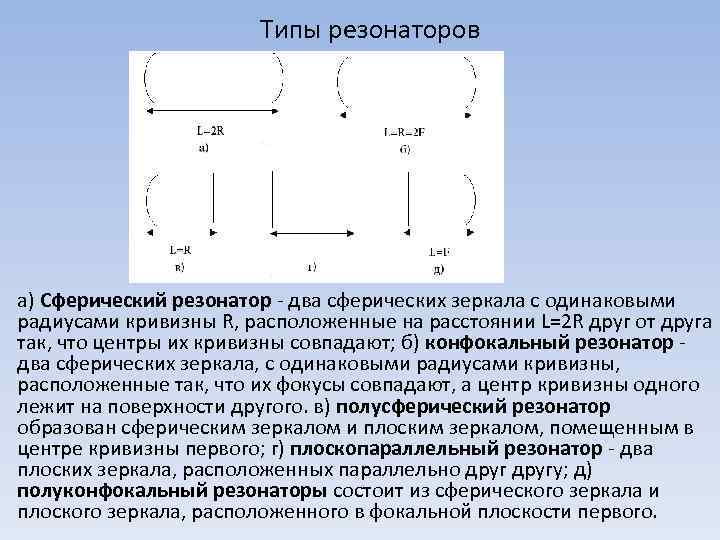
Типы резонаторов а) Сферический резонатор два сферических зеркала с одинаковыми радиусами кривизны R, расположенные на расстоянии L=2 R друг от друга так, что центры их кривизны совпадают; б) конфокальный резонатор два сферических зеркала, с одинаковыми радиусами кривизны, расположенные так, что их фокусы совпадают, а центр кривизны одного лежит на поверхности другого. в) полусферический резонатор образован сферическим зеркалом и плоским зеркалом, помещенным в центре кривизны первого; г) плоскопараллельный резонатор два плоских зеркала, расположенных параллельно другу; д) полуконфокальный резонаторы состоит из сферического зеркала и плоского зеркала, расположенного в фокальной плоскости первого.

Плоскопараллельный резонатор • При распространении плоской волны между двумя плоскими зеркалами, расположенными на расстоянии L друг от друга в результате отражений от зеркал образуется стоячая волна. • Условие образования стоячих волн вдоль оси резонатора имеет вид L = ql/2, • Тогда для резонансных частот выполняется соотношение • Тогда разность резонанс ных собственных частот соседних продольных или аксиальных мод открытого резонатора равна
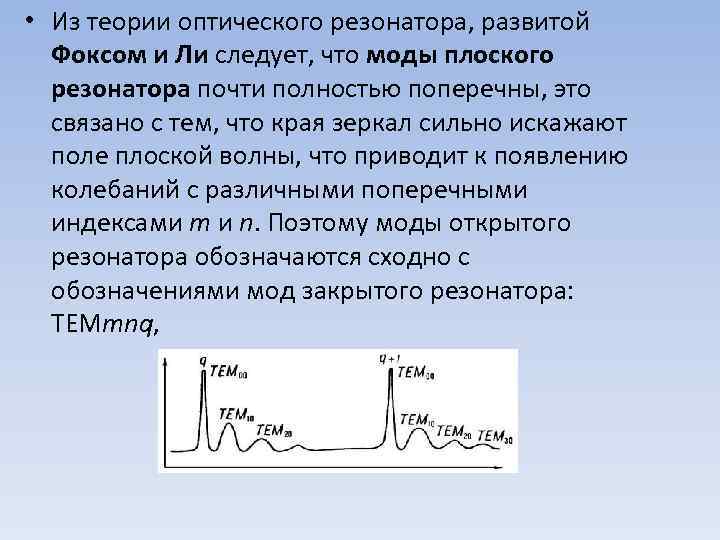
• Из теории оптического резонатора, развитой Фоксом и Ли следует, что моды плоского резонатора почти полностью поперечны, это связано с тем, что края зеркал сильно искажают поле плоской волны, что приводит к появлению колебаний с различными поперечными индексами m и n. Поэтому моды открытого резонатора обозначаются сходно с обозначениями мод закрытого резонатора: ТЕМmnq,

• если длина волны равна 500 нм и расстояние между зеркалами 25 см, то q = 106. • интервал между соседними резонансными частотами для лазера с резонатором, имеющим длину 25 см, составит • • Большинство линий лазерных переходов шире, чем 600 МГц, и, следовательно, в пределах уширенной линии содержится много продольных мод • (. . . q — 2, q — 1, q, q + 1, q + 2. . . ).

Для квадратных зеркал с длиной стороны 2 а при условии, что поперечные индексы малы, т. е. (m, n) << q, для резонансных частот плоскопараллельного резонатора справедливо соотношение: • Тогда разность частот между поперечными модами, отличающимися только значениями n на 1, равна: • моды с одинаковыми значениями q, но раз ными и n, m такими, что m 2+n 2 = const, имеют одну и ту же частоту. Такие моды называют частотно-вырожденными.
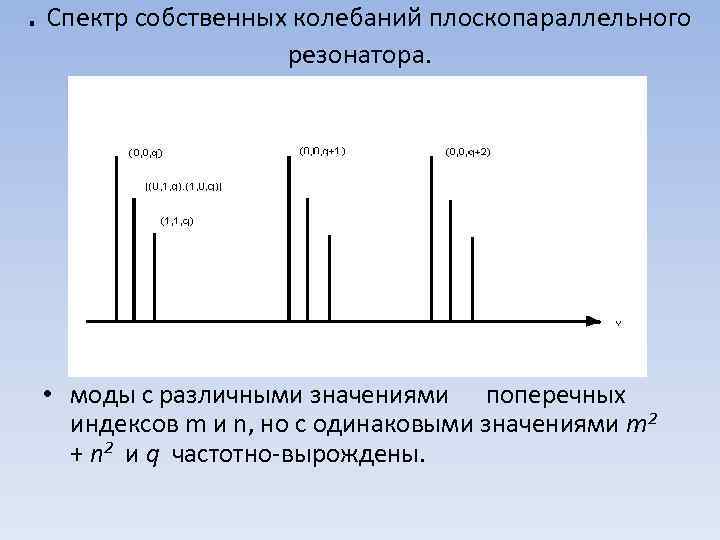
. Спектр собственных колебаний плоскопараллельного резонатора. • моды с различными значениями поперечных индексов m и n, но с одинаковыми значениями т2 + n 2 и q частотно вырождены.

• Распределение интенсивности излучения в сечении лазерного луча для различных поперечных мод. • Числами указаны значения т и п. (фотографии представлены лабораторией Bell Telephone and Spectra Physics, Inc. ) • Справа представлен спектр излучения лазера (каждой продольной моде соответствуют две поперечные

• Открытые резонаторы с плоскими зеркалами чувствительны к деформациям и перекосам зеркал, что ограничивает их применение. Этого недостатка лишены открытые резонаторы со сферическими зеркалами, в которых лучи, неоднократно отражаясь от вогнутых зеркал, не выходят за пределы огибающей поверхности. • Резонатор, состоящий из двух сферических зеркал, имеющих одинаковые радиусы R и расположенных на расстоянии L друг от друга так, что их центры кривизны совпадают (т. е. L = 2 R), называют концентрическим или сферическим резонатором

• Для обобщенного сферического резонатора резонансные частоты можно оценить по формуле • здесь • L — длина резонатора, R 1, R 2 — радиусы кривизны зеркал. Параметры g 1, g 2 определяющие устойчивость обобщенного резонатора.

Устойчивость резонаторов • Резонатор называется неустойчивым, когда произвольный луч, последовательно отражаясь от каждого из двух зеркал, удаляется на неограниченно большое расстояние от оси резонатора. • Если луч после отражения от зеркал остается в пределах ограниченной области, то резонатор называется устойчивым. Можно доказать, что обобщенный резонатор является устойчивым, если выполняется условие
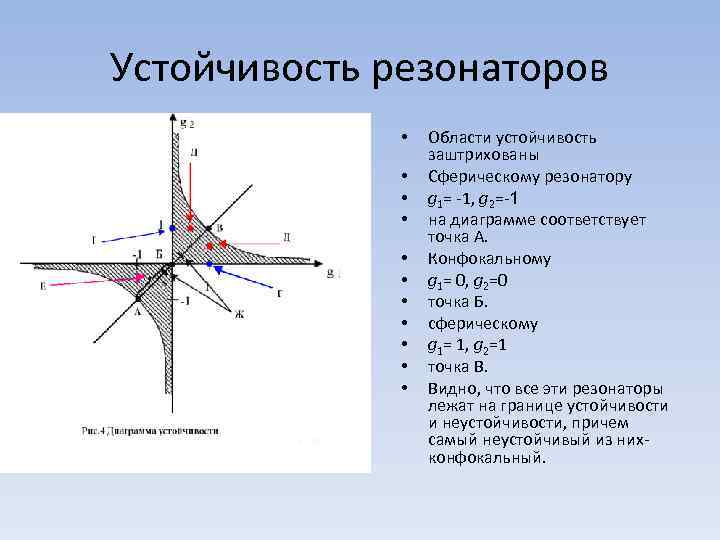
Устойчивость резонаторов • • • Области устойчивость заштрихованы Сферическому резонатору g 1= 1, g 2= 1 на диаграмме соответствует точка А. Конфокальному g 1= 0, g 2=0 точка Б. сферическому g 1= 1, g 2=1 точка В. Видно, что все эти резонаторы лежат на границе устойчивости и неустойчивости, причем самый неустойчивый из них конфокальный.

Конфокальный резонатор • Для конфокального резонатора с квадратными зеркалами с длиной стороны 2 а поперечное распределение поля (центр декартовой системы координат находится в центре резонатора описывается формулой • где Нт(х)- полиномы Эрмита. Величина w определяет размер области поперечного сечения, при выходе из которой интенсивность поля в резонаторе ( S 2 ) падает в e раз.
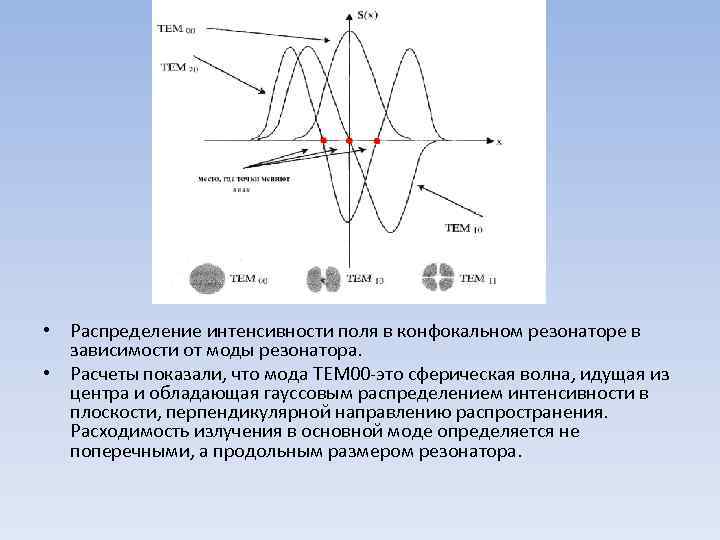
• Распределение интенсивности поля в конфокальном резонаторе в зависимости от моды резонатора. • Расчеты показали, что мода ТЕМ 00 это сферическая волна, идущая из центра и обладающая гауссовым распределением интенсивности в плоскости, перпендикулярной направлению распространения. Расходимость излучения в основной моде определяется не поперечными, а продольным размером резонатора.
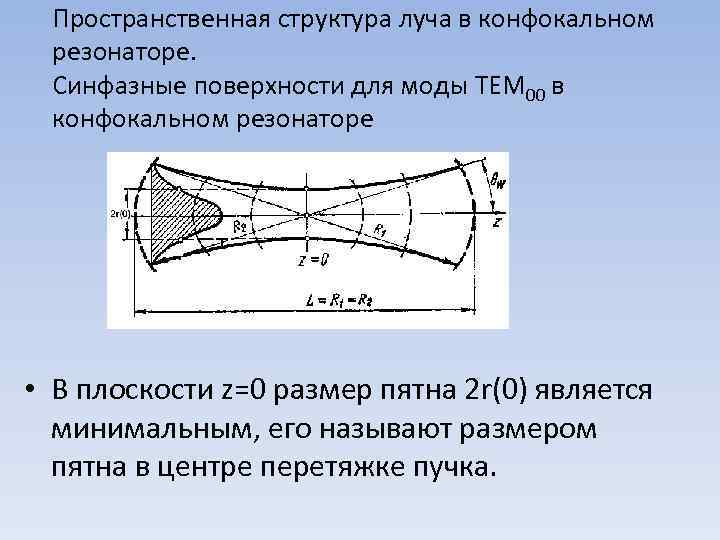
Пространственная структура луча в конфокальном резонаторе. Синфазные поверхности для моды ТЕМ 00 в конфокальном резонаторе • В плоскости z=0 размер пятна 2 r(0) является минимальным, его называют размером пятна в центре перетяжке пучка.

• Радиус кривизны волнового фронта R(z) и фаза волны (z) задаются следующими соотношениями: • где r 0 — радиус пучка в центре конфокального резонатора; — конфокальный параметр пучка; z — координата вдоль оси резонатора, отсчитываемая от его центра. • Величина R(z) берется с положительным знаком, если центр кривизны расположен слева от волнового фронта. • В центре резонатора z = 0 радиус кривизны стремится к бесконечности , т. е. волновой фронт является плоским, в то время как на зеркалах z = zk = L/2, волновой фронт совпадает с поверхностью зеркал и радиус кривизны волнового фронта является минимальным: R = L = 2 zk.

• Радиус пучка r(z) в произвольной точке конфокального резонатора можно найти следующим образом: • где r 0 — радиус пучка в центре конфокального резонатора, (размером пятна в центре перетяжки пучка. • для основного типа колебаний ТЕМ 00 размер пятна, соответствующий уменьшению напряженности поля по сравнению с центром в е раз, на поверхности зеркал в конфокальном резонаторе равен:

• Из формул следует важное соотношение между конфокальным параметром и размером пятна в центре перетяжки:

• Резонансные частоты конфокального резонатора задаются формулой • моды в конфокальном резонаторе являются вырожденными.

Метод эквивалентного резонатора расчета параметров пучка • Три основных параметра используются для характеристики сформированного пучка: • радиус перетяжки r(0), • расходимость пучка 2 и • расстояние от плоскости перетяжки до задней фокальной плоскости zp. • Тогда конфокальный параметр пучка. • Для произвольного лазерного резонатора длиной dp с зеркалами, имеющими произвольную кривизну R 1 и R 2, можно использовать следующие формулы для нахождения оптической силы ФС =2/Rc и длины эквивалентного симметричного резонатора d. C.

• Знание параметров симметричного резонатора позволяет оценить конфокальный параметр: • Для симметричного резонатора длиной L радиус перетяжки пучка основной моды можно оценить по формуле • Радиус пучка на зеркале равен:

Селекция поперечных мод. • методы селекции основаны на том, что различные поперечные моды имеют различные размеры площади поперечного сечения светового пучка и различные дифракционные потери. • 1. Введение диафрагмы в резонатор; • 2. Использование неустойчивых резонаторов. • Основная мода ТЕМ 00 имеет минимальные дифракционные потери, но в устойчивом резонаторе дифракционные потери всех мод невелики, поэтому селекция основана на различиях в распределении поля мод с различными поперечными индексами m и n. • Оценить дифракционные потери можно использовав число Френеля. Если размер диафрагмы мал, то именно он и определяет число Френеля N. • где λ длина волны, a радиус отверстия диафрагмы, l длина резонатора. • С уменьшением числа Френеля возрастают дифракционные потери.

Дифракционные потери • Зная расчетную зависимость дифракционных потерь основной и следующей за ней по порядку поперечных индексов моды от числа Френеля, можно определить требуемый радиус диафрагмы. • Дифракционные потери в резонаторе будут зависеть от типа зеркал, длины волны, радиуса зеркал (диафрагмы). • Если число Френеля достаточно велико N>10, то можно воспользоваться приближенной формулой для расчета дифракционных потерь. • αnm = 5. 23·10 2· (λn(m+1))2·N 3/2 • • • где λn(m+1) – (m+1) ый корень функции Бесселя порядка n, N – число Френеля.

• Для селекции поперечных мод размер отверстия выбирают примерно равным поперечному размеру моды, следующей за основной, т. е. TEM 01 -моды, а место расположения диафрагмы в резонаторе - там, где размеры мод отличаются наиболее сильно. • Недостатками этого способа выделения основной ТЕМ 00 -моды в устойчивом резонаторе являются: • а) малость поперечных размеров моды и, как следствие, малость используемого объема активного вещества; • б) внесение дополнительных потерь в основную моду.

• Решением является переход к неустойчивым резонаторам. дифракционные потери возрастают при переходе к высшим модам. Поэтому полные потери зависят от поперечных индексов, что приводит к подавлению высших поперечных мод и тем самым к выделению основной моды.

Методы селекции продольных мод. • Продольные моды отличаются друг от друга резонансными частотами vq и расположением узлов и пучностей стоячей волны вдоль оси резонатора. На этих двух моментах и основаны все методы селекции продольных типов колебаний. • Линия люминесценции обычно много шире линии моды резонатора ∆vp<<∆vл , поэтому возможна эффективная генерация сразу на нескольких частотах.

• Методы селекции мод • 1. уменьшении длины резонатора так, чтобы частотный интервал между соседними продольными модами • удовлетворял условию • что осуществимо в некоторых газовых лазерах, так как линии люминесценции у них узкие. Например одномодовую генерацию можно осуществить в He Ne лазере с L=15 20 см. • 2. Для подавления многомодовой генерации вводят внутрь резонатора поместить элемент, отражение ( пропускание ) которого зависит от частоты.

3. Применение составных резонаторов • Луч 0 (1→ 2→ 1): L 0 =2(L 1+ L 2). • Луч 1 (1 → 2→ (4→ 3→ 4→ 2) → 1): L(1) = 2(L 0 +L')= 2(L 1+ L 2) + 2(L 2+ L 3) • Луч k (1→ 2→ (4→ 3→ 4→ 2)К → 1): • L(l) = 2(L 0 + k L') = 2(L 1+ L 2) + 2 k(L 2 + L 3) •

• Интенсивность лучей с увеличением k резко падает, Наиболее сильные линии будут тогда, когда условия резонанса совпадут. Интенсивности совпадающих линий складываются и эти линии сильнее остальных. Условие совпадения частот имеет вид
lek_5.ppt