7-1 file_20090105191522.pptx
- Количество слайдов: 30

От положения знака в изображении числа не зависит величина, которую он обозначает. Величина, обозначаемая цифрой в записи числа, зависит от ее позиции.

Древнеегипетская десятичная • • Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 100 и т. д. использовались специальные значки — иероглифы. Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной.

1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем ряду должно быть столько же палочек, сколько и в верхнем, или на одну больше. 10. Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. 100. Это мерная веревка, которой измеряли земельные участки после разлива Нила. 1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка. 10 000. "В больших числах будь внимателен!" - говорит поднятый вверх указательный палец. 100 000. Это головастик. Обычный лягушачий головастик. 1 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф 10 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца

Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду. Попробуйте сложить эти два числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Обычному человеку это не под силу.

• • В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером является римская система. В римской системе в качестве цифр используется латинские буквы: I 1 V 5 X 10 L 50 C 100 D 500 M 1000 • Число в римской системе счисления обозначается набором стоящих подряд цифр. • В такой записи числа значение цифры не зависит от ее места в записи числа.

• • Число в римской системе счисления обозначается набором стоящих подряд цифр. Значение числа равно: Сумме значений идущих подряд нескольких одинаковых цифр (группа первого вида); III=3. Разности значений двух цифр, если слева от большей цифры стоит меньшая (группа второго вида). IV=4. ü Левая цифра может быть меньше правой максимум на один порядок: ü перед L(50) и C(100) может стоять только Х(10); ü перед D(500) и M(1000) – только С(100); ü перед V(5) – только I(1). Сумме значений групп и цифр, не вошедших в группы первого и второго видов. CLVI=156. Рядом не должно стоять более трех одинаковых цифр. • • Число 32 =XXXII = (X+X+X)+(I+I)= 30+2 Число 444 = CDXLIV=(D-C)+(L-X)+(V-I)= 400+40+4. Число 1974 в римской системе счисления имеет вид MCMLXXIV= M+(M-C)+L+(X+X)+(V-I)=1000+900+50+20+4. • • MCMXCVIII = 1000+(1000 -100)+(100 -10)+5+1+1+1 = 1998

О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века. В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника. Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.

Вавилонская шестидесятеричная система • • Началом ее появления считают второе тысячелетие до н. э. Числа в этой системе составлялись из знаков двух видов: • • Число 60 и остальные степени 60 обозначалось так же, как 1 . Для определения значения числа его запись нужно было разбить на разряды справа налево. Чередование групп одинаковых цифр соответствовало чередованию разрядов: 132= • • ? ?

• Значение числа определяли по значениям составляющих его цифр, но с учетом того, что цифры в каждом последующем разряде «весили» в 60 раз больше таких же цифр предыдущего разряда. Получается, что в числах от 1 до 59 значение цифры не зависело от ее номера, а для чисел, больших или равных 60, значение цифры зависело от ее позиции в записи числа. Здесь могла возникнуть путаница: знак единицы можно было трактовать как любую степень числа 60; число • могло быть равно 92 (60+30+2) или 3632 (3600+30+2); • • могло быть равно как 444 (7*60+24), так и 7*3600+24. Это происходило по причине отсутствия 0. Впоследствии вавилоняне ввели знак для обозначения пропущенного шестидесятеричного разряда. • Но в конце числа этот символ обычно не ставился, так что он не являлся нулем в нашем понимании. Такая система счисления – первая, основанная на позиционном принципе. Отмечают большую роль этой системы счисления в математике и астрономии. Так, мы до сих пор делим час на 60 мин, а минуту – на 60 секунд, окружность на 360 частей (градусов).

Древнеегипетская десятичная непозиционная система счисления • Возникновение этой системы относят ко второй половине третьего тысячелетия до н. э. В ней использовались специальные знаки для обозначения степеней десяти: • Число 345 записывалось так: . Каждая цифра в записи числа не должна была повторяться более 9 раз. В основе палочной и древнеегипетской систем счисления лежал принцип сложения, согласно которому значение числа равно сумме значений цифр, участвующих в записи числа. В такой записи числа значение цифры не зависит от места, которое она занимает в записи числа.

ДРЕВНЯЯ РУСЬ • Пример использования этих знаков на Руси: квитанции об уплате податей (ясака), которые заполняли сборщики податей уплачивали

• • • Славянская кириллическая десятеричная алфавитная Эта нумерация была создана вместе со славянской алфавитной системой для перевода Библии Кириллом и Мефодием в IX веке. Эта форма записи чисел имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.
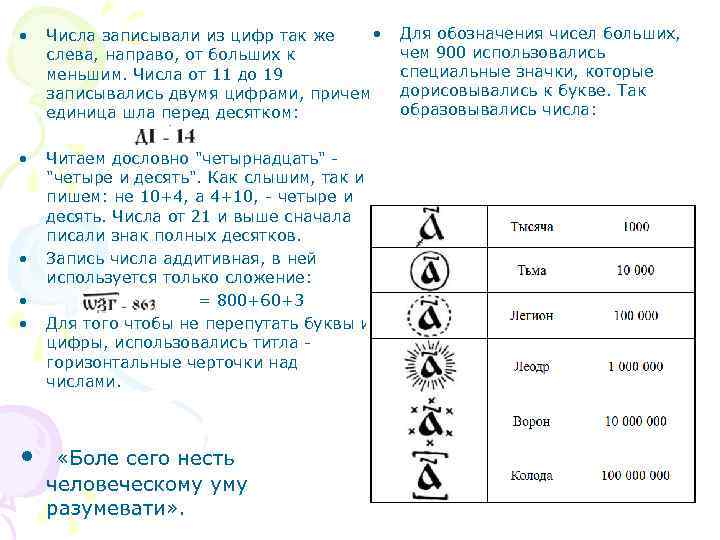
• • Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком: • Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше сначала писали знак полных десятков. Запись числа аддитивная, в ней используется только сложение: = 800+60+3 Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами. • • «Боле сего несть человеческому уму разумевати» . Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:

Алфавитные системы счисления В алфавитной системе счисления проглядывают зачатки позиционной системы, т. к. для обозначения единиц разных разрядов применялись одни и те же буквы, только с добавлением специальных обозначений. Такие системы счисления были неудобны для операций с большими числами. В ходе развития человеческого общества эти системы уступили свое место позиционным.

Индийская мультипликативная система • • Позиционные системы счисления возникли независимо друг от друга в древнем Вавилоне, у индейцев племени майя и, наконец, в Индии. В таких системах счисления сначала возникли специальные обозначения, добавляемые к десяткам и сотням. Если обозначим через Х десятки, а через Y – сотни, то 323=3 Y 2 X 3. Современная десятичная система счисления возникла примерно в V в. Н. э. в Индии. Возникновение этой системы стало возможным после появления нуля. Теперешнее обозначение 0 впервые появилось в Греции после знакомства греческих ученых с астрономическими наблюдениями вавилонян. Для обозначения нулевого разряда греки стали использовать букву О – первую букву слова «OUDEN» - НИЧТО. Индийцы соединили свою мультипликативную систему с греческим нулем и алфавитными принципами записи чисел в Греции.

Но эта система и цифры, используемые в ней, называются арабскими, т. к. в Европу такие цифры «привезли» арабские купцы вместе со своими товарами. В Европе такая система счисления получила распространение с начала XII века. Решающую роль в её распространении сыграло руководство, составленное в IX веке Мухаммедом из Хорезма. Оно было переведено на латинский язык в XII веке. Правила вычитания, умножения и деления «столбиком» , были тоже разработаны еще в IX веке выдающимся математиком Мухаммедом ибн Мусой аль Хорезми. Такие правила по его имени получили название algorithmi (алгоритмы).

Он был итальянским математиком. Благодаря его книге «Liber Abaci» Европа узнала индо -арабскую систему чисел, которая позднее вытеснила римские числа .

Позиционную систему счисления называют традиционной, если ее базис образует члены геометрической прогрессии, а значения цифр есть целые неотрицательные числа. Базиспоследовательность чисел каждая из которых задает вес соответствующего разряда. Знаменатель P геометрической прогрессии, члены которой образуют базис традиционной системы счисления, называется основанием этой системы счисления. Традиционные системы счисления с основанием P иначе называют P- ичным.

• • Система счисления или нумерация- это способ записи чисел. Символы, при помощи которых записываются числа, называются цифрами, а их совокупность – алфавитом системы счисления. Количество цифр, составляющих алфавит, называется его размерностью. Система счисления называется позиционной, если количественный эквивалент цифры зависит от ее положения в записи числа. В привычной нам десятичной системе значения числа образуется следующим образом: значение цифр умножаются на «вес» соответствующих разрядов и все полученные значения складываются. Например, 5047=5*1000+0*100+4*10+7*1. Такой способ образования значения числа называется аддитивно-мультипликативным.

Где А-само число, q-основание системы счисления, а-цифры данной системы счисления, n-число разрядов целой части числа, m-число разрядов дробной части числа. Пример: 32478 = единицы десятки сотни тысячи
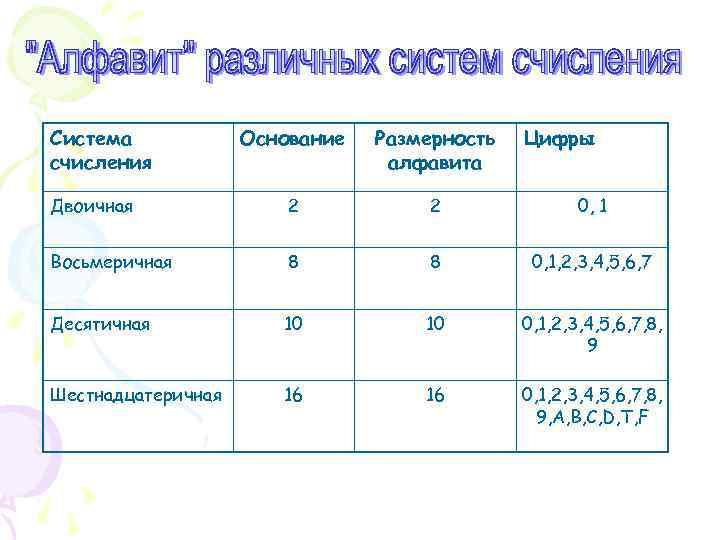
Система счисления Основание Размерность алфавита Цифры Двоичная 2 2 0, 1 Восьмеричная 8 8 0, 1, 2, 3, 4, 5, 6, 7 Десятичная 10 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Шестнадцатеричная 16 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, T, F
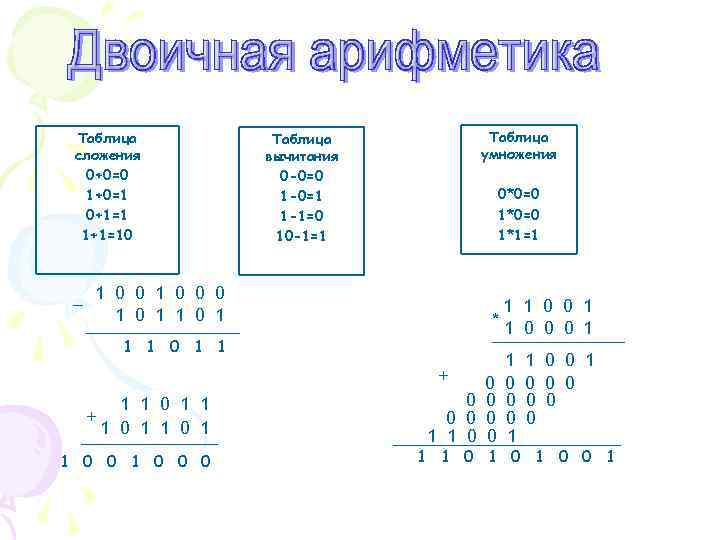
Таблица сложения 0+0=0 1+0=1 0+1=1 1+1=10 Таблица умножения Таблица вычитания 0 -0=0 1 -0=1 1 -1=0 10 -1=1 0*0=0 1*1=1 _ 1 0 0 0 1 1 1 0 0 1 *1 0 0 0 1 1 1 0 1 1 + + 1 1 0 1 1 0 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1
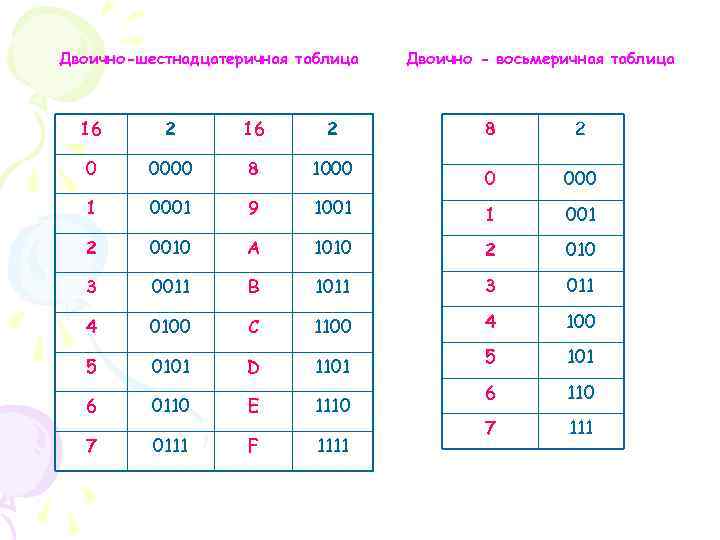
Двоично-шестнадцатеричная таблица 16 2 0 0000 8 1000 1 0001 9 2 0010 3 Двоично - восьмеричная таблица 8 2 0 000 1001 1 001 А 1010 2 010 0011 В 1011 3 011 4 0100 С 1100 4 100 5 0101 D 1101 5 101 6 110 7 111 6 0110 Е 1110 7 0111 F 1111
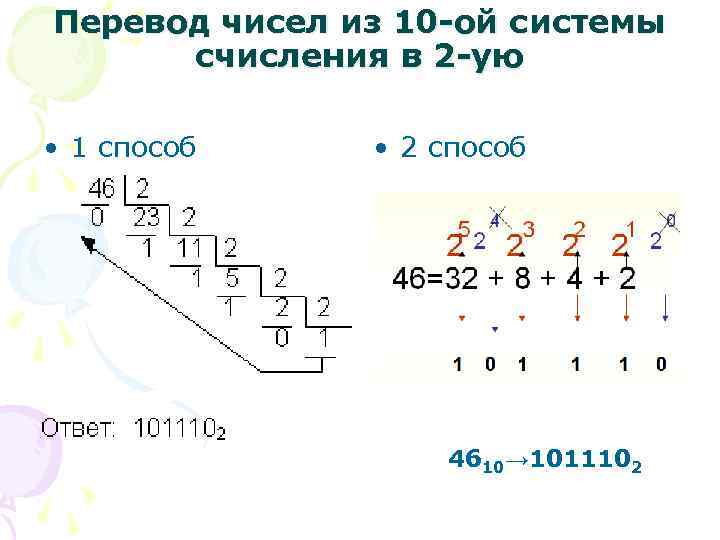
Перевод чисел из 10 -ой системы счисления в 2 -ую • 1 способ • 2 способ 4610→ 1011102

Двоичная 15 14 1 Восьмеричная 315 24 75 72 3 2 7 6 1 2 3 2 1 8 39 8 32 4 7 Шестнадцатеричная 315 16 155 144 11 (В) 16 1 9 16 16 3 1 315 10 = 13 В 16

Двоичная 0 1875 0 3750 0 7500 Шестнадцатеричная х 2 Восьмеричная х 2 0 1875 х 8 1 5000 1 4 х 2 0000 х 8 0000 0 1875 х 16 3 0000

Перевод из 10 -ной СС Перевод осуществляется отдельно для целой и отдельно для дробной части числа. Переведем, например, число 24. 8510 в 2 -ную СС. 24 2 0 12 2 2410 = 110002 0 6 2 0 3 2 1 1

Ей было 1100 лет. Она в 101 класс ходила. В портфеле по 100 книг носила. Все это правда, а не бред. Когда пыля десятком ног. Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий, Она ловила каждый звук Своими десятью ушами, И 10 загорелых рук Портфель и поводок держали. И 10 темно-синих глаз Оглядывали мир привычно. Но станет все совсем обычным, Когда поймете наш рассказ. ОТВЕТ

Ей было 12 лет. Она в 5 класс ходила. В портфеле по 4 книг носила. Все это правда, а не бред. Когда пыля десятком ног. Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий, Она ловила каждый звук Своими десятью ушами, И 2 загорелых рук Портфель и поводок держали. И 2 темно-синих глаз Оглядывали мир привычно. Но станет все совсем обычным, Когда поймете наш рассказ.
7-1 file_20090105191522.pptx