Остаточный член формулы Тейлора Формула Тейлора для

Остаточный член формулы Тейлора

Формула Тейлора для Оценим остаток

] - неизвестная функция Зафиксируем x и введём вспомогательную ф-цию

Т. к. , то по теореме Ролля

Остаточный член в форме Лагранжа Это погрешность при замене функции многочленом Тейлора

Если при Остаточный член в форма Пеано

Представление функций многочленом Тейлора

Теорема (Формула Тейлора) Если в окрестности точки , то

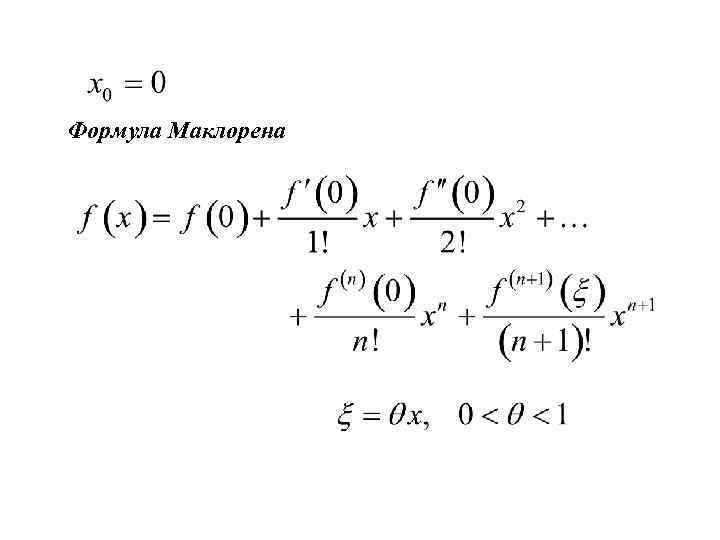Формула Маклорена

формула Лагранжа Формулы для приближённых вычислений

Формулы Маклорена для основных ф-ций

Пример Найти число е с точностью 0, 001

Приложение формулы Тейлора к исследованию функций

Главная часть бесконечно малой

- главная часть

Пример

Экстремумы функции

Определение Теорема (необходимое условие существования экстремума)

Другая формулировка Определение

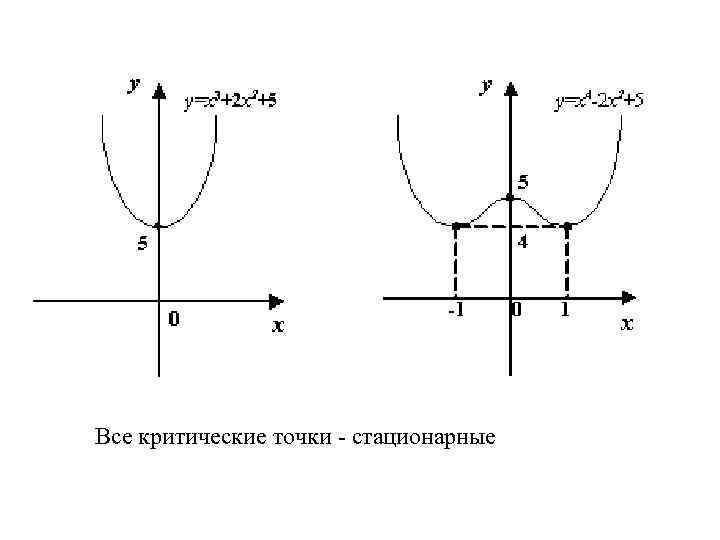Все критические точки - стационарные

Критическая точка - min

Критическая точка не является экстремальной!

Теорема (Достаточное условие существования экстремума)

Доказательство

Теорема (Достаточное условие существования экстремума)

Доказательство

y y f(x) f(x 0) f(m)(x 0)>0 m =2 k О x 0 m =2 k+1 x О x 0 x

Выпуклость и вогнутость кривой Точки перегиба

y M(x 0 , y 0) y f(x) M(x 0 , y 0) y кр y кас О x 1 x 0 Выпуклая Кривая выше касательной x О x 1 x 0 Вогнутая Кривая ниже касательной x

Теорема + - --

Определение Точка, при переходе через которую меняется кривизна кривой, называется точкой перегиба Теорема (Необходимое условие точки перегиба) - точка перегиба

Теорема (Достаточное условие точки перегиба) Если при переходе через точку меняет знак, то - точка перегиба

Теорема (Достаточное условие точки перегиба) Если , то - точка перегиба (младшая из производных, отличных от нуля, имеет нечётный порядок )

Асимптоты кривой

Определение

Горизонтальная асимптота —прямая вида при условии существования предела .

Наклонная асимптота — прямая вида при условии существования пределов

горизонтальная асимптота является частным случаем наклонной при