Презентация1.ppt
- Количество слайдов: 25

Особенности ECDSA (Elliptic Curve Digital Signature Algorithm) — алгоритм с открытым ключом для создания цифровой подписи, аналогичный по своему строению DSA, но определённый в отличие от него не над полем целых чисел, а в группе точек эллиптической кривой. o Стойкость алгоритма шифрования основывается на проблеме дискретного логарифма в группе точек эллиптической кривой. В отличие от проблемы простого дискретного логарифма и проблемы факторизации целого числа, не существует субэкспонециального алгоритма для проблемы дискретного логарифма в группе точек эллиптической кривой. По этой причине «сила на один бит ключа» существенно выше в алгоритме, который использует эллиптические кривые. [1] o Д. Брауном (Daniel R. L. Brown) было доказано, что алгоритм ECDSA не является более безопасным, чем DSA. Им было сформулировано ограничение безопасности для ECDSA. o Алгоритм ECDSA в 1999 г. был принят, как стандарт ANSI, в 2000 г. — как стандарт IEEE и NIST. Также в 1998 г. алгоритм был принят стандартом ISO. Несмотря на то, что стандарты ЭЦП созданы совсем недавно и находятся на этапе совершенствования, одним наиболее перспективных из них на сегодняшний день является ANSI X 9. 62 ECDSA от 1999 — DSA для эллиптических кривых.

Параметры алгоритма o o o Для подписывания сообщений необходима пара ключей — открытый и закрытый. При этом закрытый ключ должен быть известен только тому, кто подписывает сообщения, а открытый — любому желающему проверить подлинность сообщения. Также общедоступными являются параметры самого алгоритма. Выбор хэш-функции H(x). Для использования алгоритма необходимо, чтобы подписываемое сообщение являлось числом. Хеш-функция должна преобразовать любое сообщение в последователность битов, которые можно потом преобразовать в число. Выбор большого простого числа q — порядок одной из циклических подгруппы точек эллиптической кривой. Замечание: Если размерность этого числа в битах меньше размерности в битах значений хэш-функции H(x) то используются только левые биты значения хэш-функции. Простым числом p обозначается характеристика поля координат Fp.

Генерирование ключей ECDSA o Для простоты будем рассматривать эллиптические кривые над o o полем Fp, где Fp — конечное простое поле. Причем, если необходимо, конструкцию можно легко адаптировать для эллиптических кривых над другим полем. Пусть E — эллиптическая кривая, определенная над Fp, и P — точка простого порядка q кривой E(Fp). Кривая E и точка P являются системными параметрами. Число p — простое. Каждая пользовательница Алиса конструирует свой ключ посредством следующих действий: Выбирает случайное или псевдослучайное целое число x из интервала [1, q − 1]. Вычисляет произведение (кратное) Q = x·P. Открытым ключом пользовательницы Алисы A является точка Q, а закрытым — x.

Вычисление цифровой подписи o Для того, чтобы подписать какое-либо сообщение, для которого o o o o подсчитано значение h хэш-функции H, пользователь A должен сделать следующее: Выбрать случайное целое число. Вычислить и положить в , где r получается из целого числа x 1 между 0 и (p − 1) приведением по модулю q. Замечание: если r = 0, то уравнение подписи не зависит от секретного ключа x, и следовательно, (r, s) не подходит в качестве цифровой подписи. Значит, в случае r = 0 необходимо вернуться к шагу 1. Вычислить k − 1(mod q) и положить , где h — значение хеш-функции подписываемого сообщения. Замечание: если s = 0, то значение s − 1(mod q), нужное для проверки, не существует. Значит, в случае s = 0 необходимо вернуться к шагу 1. Подписью для сообщения является пара целых чисел (r, s).

Проверка цифровой подписи o o o Для того, чтобы проверить подпись пользовательницы Алисы (r, s) на сообщение, пользователь Борис B должен сделать следующее: Получить подтвержденную копию открытого ключа Q пользовательницы А; Проверить, что числа r и s являются целыми числами из интервала [1, q − 1], и вычислить значение хеш-функции h от сообщения; Вычислить и ; Вычислить , и относительно x 0, как целого числа между 0 и (p − 1), положить ; Принять подпись, если и только если v = r. Заметим, что, если пользовательница Алиса вычислила свою подпись правильно, то , так как k = s − 1(h + xr)(mod q), и поэтому v = r. Для подтверждения публичного ключа Q нужно проделать следующее (O здесь обозначает бесконечно удалённую точку): Проверить, что Q не равно O и координаты верны; Проверить, что Q лежит на кривой; Проверить, что q. Q = O;

Общие сведения об эллиптических кривых: o Эллиптические кривые названы так потому, что они описываются o o кубическими уравнениями, подобными тем, которые используются для задания кривой эллипса. Эллиптической кривой E над полем F называется гладкая кривая, задаваемая уравнением Вейерштрасса: где Для обозначения эллиптической кривой используют запись E или E/F, чтобы подчеркнуть, что кривая определена над полем F. Точка P = (x 0, y 0) E называется невырожденной (гладкой), если для многочлена верно по крайней мере одно из условий: или Эллиптическая кривая E/F является невырожденной (гладкой), если каждая точка (x, y) E является невырожденной.

Общие сведения об эллиптических кривых(1) o o o o На множестве точек кривой вводится операция сложения точек по следующему закону: сумма любых 3 -х точек эллиптической кривой, лежащих на 1 -й прямой, равна O. Геометрически точка O лежит в бесконечности на прямой пересекающей противоположные точки, в положительном направлении оси ординат. Множество точек (x, y) E , содержащее, кроме того, бесконечно удаленную от кривой точку O, с введенной на нем операцией сложения точек образуют конечную абелеву (коммутативную) группу, которая называется группой точек эллиптической кривой. Точка O является аддитивной единицей в данной группе. В группе точек эллиптической кривой E вводится операция скалярного умножения (умножения точки на число), определяемая следующей формулой: , где P E, Q E, a N. Для практического применения в криптографии используются эллиптические кривые, заданные над полями Галуа (простыми полями). Пусть задано простое число p > 3. Тогда эллиптической кривой E, определенной над простым конечным полем Fp, называется множество пар чисел (x, y), x, y Fp, которые удовлетворяют тождеству: где a, b Fp и (4 a 3 + 27 b 2) 0 (mod p).

Общие сведения об эллиптических кривых(2) o o o o o Под порядком эллиптической кривой понимают порядок группы точек эллиптической кривой (число различных точек на E, включая точку O). Для эллиптической кривой E заданной над простым полем Fp, порядок m группы точек данной кривой зависит от размера поля, определяемого простым числом p, и удовлетворяет неравенству: Каждая точка P эллиптической кривой над простым полем E(Fp) образует циклическую подгруппу G группы точек эллиптической кривой. Порядок циклической подгруппы точек эллиптической кривой (число точек в подгруппе) называется порядком точки эллиптической кривой. Точка P E(Fp) называется точкой порядка q, если: , где q – наименьшее натуральное число, при котором выполняется данное условие. Причем: m = nq, n Z, n>=1. Образующую точку P E(Fp) необходимо выбрать так, чтобы порядок q циклической подгруппы был достаточно большим. Далее в данной подгруппе производится вычисление открытого ключа по данному закрытому. Выбирается случайное число 0 < d < q, которое будет являться закрытым ключом и вычисляется точка Q = d. P, которая будет являться открытым ключом.

Требования к эллиптической кривой o o o o o Для того, чтобы избежать известных атак, основанных на проблеме дискретного логарифма в группе точек эллиптической кривой, необходимо, чтобы число точек эллиптической кривой E делилось на достаточно большое простое число n. Стандарт ANSI X 9. 62 требует n > 2160. Уравнение эллиптической кривой строится специфическим образом, используя случайные/псевдослучайные коэффициенты. Главными параметрами при построении эллиптической кривой являются: размерность поля p, где p явлется простым числом; два элемента поля Fp — a и b, определенные уравнением эллиптической кривой E, где E имеет вид: y 2 = x 3 + ax + b, где a, b Fp, и 4 a 3 + 27 b 2 0 (mod p). два элемента поля Fp — x. G и y. G, которые определяют конечную точку G = (x. G, y. G) — генератор группы E(Fp) порядок q точки G, где q > 2160 и q > 4 сомножитель h = #E(Fp)/q, где обозначение #E(Fp) означает порядок группы точек эллиптической кривой E(Fp).

Генерация главных параметров o Один из способом генерирования криптографически надежных o o o параметров заключается в следующем: Выбираем коэффициенты a и b специфическим образом используя в вычислениях случайные/псевдослучайные числа. Пусть E — эллиптическая кривая — y 2 = x 3 + ax + b; Вычисляем ; Проверяем, что N имеет делитель, который является большим простым числом q(q > 2160 и. Если нет, то нужно вернуться на шаг 1. Проверяем, что q не делит pk − 1 для каждого k, . Если нет, то нужно вернуться на шаг 1; Проверяем, что. Если нет, то нужно вернуть на шаг 1; Берем случайную точку и положить G = (N / q)G'. Повторяем до тех пор пока.

Преимущества ECDSA над DSA o ECDSA является очень привлекательным алгоритмом для реализации ЭЦП. Самым важным преимуществом ECDSA является возможность его работы на значительно меньших полях Fp. Как, в общем, с криптографией эллиптической кривой, предполагается, что битовый размер открытого ключа, который будет необходим для ECDSA, равен двойному размеру секретного ключа в битах. Для сравнения, при уровне безопасности в 80 бит (то есть атакующему необходимо примерно 280 версий подписи для нахождения секретного ключа), размер открытого ключа DSA равен, по крайней мере, 1024 бит, когда как открытого ключа ECDSA — 160 бит. С другой стороны размер подписи одинаков и для DSA, и для ECDSA: 4 t бит, где t — уровень безопасности, измеренный в битах, то есть — примерно 320 бит для уровня безопасности в 80 бит.

Слабость цифровой подписи ECDSA Есть мнение, что новый стандарт небезопасен, так как позволяет имитировать подмену подписи. По его мнению, недостаток ECDSA в том, что этот стандарт позволяет рядовому пользователю выбрать свои секретный и открытый ключи так, что подписи для двух известных заранее сообщений совпадут. Если q. G=0, то (q-1)G = -G, следовательно справедливы равенства: c 1 = x. G = c 2 = x(q-1)G = c, где 0 - бесконечно удаленная точка эллиптической кривой (нейтральный элемент относительно операции +). Положим случайные вычеты q 1 и q 2 равными 1 и (q-1). Отметим также, что (q-1)-1 = (q-1) (mod q). Подберем две одинаковые подписи для сообщений m 1 и m 2. Уравнения подписи имеют вид: d 1 = u 1 -1 (m 1 + sc) (mod q) = (m 1 + sc) (mod q) d 2 = u 2 -1 (m 2 + sc) (mod q) = (q-1)(m 2 + sc) (mod q) Нам нужно, чтобы выполнялось равенство d 1 = d 2. Получим уравнение: m 1+sc = (q 1)(m 2 +sc) (mod q) Отсюда легко находится s: 2 cs = (q-1)(m 1 + m 2) (mod q)Так как q - простое число, то это уравнение однозначно разрешимо относительно s. Таким образом, мы получили две одинаковые подписи для двух заранее выбранных сообщений.

Практическая реализация На сегодняшний день реализация электронных цифровых подписей осуществляются программным образом. Для создания подобных продуктов используют специальные программные пакеты, позволяющие создавать криптографические приложения с использованием различных внешних устройств безопасности.

Основные проблемы криптостойкости: o o o Проблема нахождения закрытого ключа является проблемой нахождения дискретного логарифма в группе точек эллиптической кривой определенной над простым полем. Стойкость протоколов криптографии на эллиптических кривых в конечных полях основана на сложности решения проблемы дискретного логарифма. Эта проблема имеет место в каждом случае, когда задана некоторая циклическая группа G с образующим элементом a. Тогда любой элемент y G может быть вычислен как: y = ax, где x Z (Z – кольцо целых чисел). При известном x вычислить y довольно легко, а сделать обратное преобразование, то есть вычислить x по известному y очень трудно. Под словами очень трудно здесь понимается отсутствие алгоритма решения данной задачи за субполиномиальное время (практически задача может быть решена полным перебором). Криптосистемы цифровой подписи на основе эллиптических кривых с длиной ключа 160 бит имеют одинаковую стойкость с криптосистемами DSA и Эль-Гамаля с длиной ключа 1024 бита. Очевидно, что в ближайшем будущем данные системы займут доминирующее положение в криптографии с открытым ключом. Однако, при их широком распространении и применении, большие силы криптоаналитиков будут направлены на поиск новых, более быстрых, алгоритмов решения проблемы дискретного логарифма в группе точек эллиптических кривых. Скорее всего такие алгоритмы будут найдены, как это уже произошло с проблемами разложения больших чисел на множители (RSA) или дискретного логарифма в простом поле (DSA, Эль-Гамаль).

Электронная цифровая подпись Механизм электронной цифровой подписи (ЭЦП) возник как побочный эффект криптографии с открытым ключом. Поэтому характерное для систем с открытым ключом разделение ключа на 2 части - секретную и несекретную - позволяет реализовать возможность проверки подлинности без возможности подписать другой документ. Цифровая подпись - это конечная цифровая последовательность, зависящая от самого сообщения или документа и от секретного ключа, известного только подписывающему субъекту, предназначенная для установления авторства. Так как цифровая подпись строится на базе криптосистемы с открытым ключом, то необходимо иметь пару ключей - секретный и открытый. Секретный ключ используется для формирования цифровой подписи, поэтому его нужно хранить в тайне. А открытый ключ используется для проверки соответствия подписи документу, поэтому он должен быть опубликован, например, в общедоступном каталоге.

Механизм сертификатов(1) При использовании цифровой подписи нужно защищать только свои личные секретные ключи. А открытые ключи им нужно использовать совместно. Хранить их в секрете нет необходимости, нужна лишь возможность идентифицировать открытый ключ другой стороны. Поэтому для применения цифровой подписи критическое значение имеет доверие к соответствию между известным субъектом и его открытым ключом. Субъект B может доверять открытому ключу субъекта A, если A передал ему ключ безопасным способом. Но безопасность передачи обеспечивается только защищенными средствами связи. Более вероятно, что B получил открытый ключ A с помощью незащищенного средства связи (например, из общего каталога), поэтому нужен механизм, который может обеспечить B уверенность в том, что имеющийся у него открытый ключ действительно принадлежит A, а не кому-либо другому. Один их таких механизмов основан на сертификатах (certificate), выдаваемых центром сертификации (certification authority). Сертификаты обеспечивают механизм надежной связи между открытым ключом и субъектом, которому принадлежит соответствующий личный ключ. Сертификат - это цифровой документ, который содержит открытый ключ субъекта (subject public key) и подписан электронной цифровой подписью его издателя (issuer). Сертификат также содержит сведения о владельце открытого ключа, например, информацию, которая его дополнительно идентифицирует

Механизм сертификатов(2) Таким образом, выдавая сертификат, издатель удостоверяет подлинность связи между открытым ключом субъекта и информацией, его идентифицирующей. В настоящее время наиболее часто используются сертификаты на основе стандарта Международного союза телекоммуникаций ITU-T X. 509 версии 3 и рекомендаций IETF (Internet Engineering Task Force) RFC 2459. Например, формат сертификата X. 509 принят в протоколах S/MIME, IP Security, а также SSL/TLS и SET. Кроме того, это базовая технология, используемая в инфраструктуре открытых ключей операционной системы Windows 2000. Однако это не единственный вид сертификатов. Например, система защиты сообщений электронной почты PGP (Pretty Good Privacy) использует свою специфическую форму сертификатов. Центр сертификации (ЦС) --- это служба, которая выдает сертификаты. Центр сертификации является гарантом связи между открытым ключом субъекта и содержащейся в сертификате информацией по идентификации этого субъекта. Различные ЦС устанавливают и гарантируют эту связь различными способами, поэтому прежде чем доверять сертификатам того или иного ЦС, следует ознакомиться с его политикой и регламентом.

Подтверждение доверия(1) o Когда B получает подписанное сообщение, у него возникает важный вопрос: можно ли этой подписи доверять? Иными словами, действительно ли эта подпись принадлежит отправителю сообщения? Если B сможет найти сертификат открытого ключа A, выданный тем центром сертификации, которому он доверяет, то он получит убедительное подтверждение того, что открытый ключ A действительно принадлежит A. Итак, у B появится веское основание полагать, что открытый ключ принадлежит именно A, если он найдет сертификат, который: - имеет действительную с криптографической точки зрения подпись его издателя; - подтверждает связь между именем A и открытым ключом A; - выдан центром сертификации, которому B доверяет.

Подтверждение доверия(2) Если B найдет такой сертификат открытого ключа A, то он сможет проверить подлинность этого сертификата с помощью открытого ключа центра сертификации. Однако теперь у B возникает следующий вопрос: как убедиться в том, что этот открытый ключ действительно принадлежит данному центру сертификации? B нужно найти сертификат, удостоверяющий подлинность этого центра сертификации. Таким образом в процессе проверки сертификата B продвигается по цепочке сертификатов (certification path). В конце цепочки сертификатов, ведущей от сертификата открытого ключа A через ряд центров сертификации, находится сертификат, выданный тем ЦС, которому B полностью доверяет. Такой сертификат называется доверенным корневым сертификатом (trusted root certificate), поскольку он образует в иерархии связей «открытые ключи – личность» корень (самый верхний узел), который B считает надежным. Если B явно решит доверять этому доверенному корневому сертификату, то он неявно будет доверять всем сертификатам, выданным доверенным корневым сертификатом и всеми сертифицированными им ЦС. Набор доверенных корневых сертификатов, которым B доверяет явно - это единственная информация, которую B должен получить надежным способом. На этом наборе сертификатов базируется его система доверия и обоснование надежности инфраструктуры открытых ключей.

Схемы электронной цифровой подписи Аппарат электронной цифровой подписи позволяет решать задачи проверки целостности и их авторства (без возможности отречения), разумеется, если используются стойкие алгоритмы формирования ЭЦП, надежные криптографические протоколы и сохранен в тайне секретный ключ. Поэтому для того, чтобы документы, подписанные ЭЦП, имели юридическую силу, развитые государства принимают стандарты на алгоритмы ЭЦП, кроме того, существует ряд коммерческих алгоритмов, которые хоть в среднем и слабее национальных, однако достаточно надежны для коммерческого уровня при разумном выборе длины ключей. Ниже будут описаны 9 алгоритмов формирования цифровой подписи:
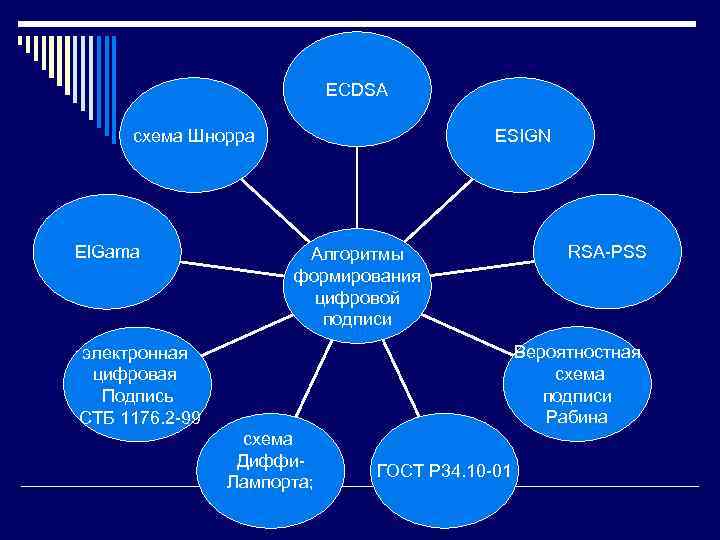
ECDSA схема Шнорра El. Gama ESIGN Алгоритмы формирования цифровой подписи RSA-PSS Вероятностная схема подписи Рабина электронная цифровая Подпись СТБ 1176. 2 -99 схема Диффи. Лампорта; ГОСТ Р 34. 10 -01

Функции (продолжение) o o Установить n-битный хэш-код в ноль. Для каждого n-битного блока данных выполнить следующие операции: n n o o o сдвинуть циклически текущий хэш-код влево на один бит; выполнить операцию XOR для очередного блока и хэш-кода. Это даст эффект "случайности" входа и уничтожит любую регулярность, которая присутствует во входных значениях. Будем пользоваться хэш-схемой СВС. Введение в криптографию на эллиптических кривых В 80 -е годы были разработаны, а в 90 -е нашли широкое распространение системы цифровой подписи, построенные на использовании методов несимметричной криптографии. Основными из них являлись алгоритмы цифровой подписи RSA, DSA, Эль-Гамаля. Эти системы были отнесены к классу вероятно-стойких или доказуемо-стойких, что объясняется тем, что доказательство их стойкости сводилось к доказательству сложности решения определенных математических задач при соответствующих значениях (размерах) общесистемных параметров. Так доказательство стойкости RSA систем сводилось в основном к доказательству сложности решения задач факторизации модуля преобразования N. Доказательство стойкости алгоритмов Эль-Гамаля и DSA сводилось к доказательству сложности решения задачи нахождения дискретного логарифма в конечном поле. При этом по мере расширения применения указанных стандартов активизировались усилия по их взлому. Появились совершенно новые разделы математики, позволяющие существенно уменьшить вычислительную сложность решения указанных задач. Например, создание средств решения таких задач на основе общего решета числового поля в сочетании с применением мощных компьютеров сделало возможным взлом систем с параметрами, используемыми на практике. Иначе говоря, средства криптоанализа, в смысле математики и производительности криптоаналитических систем, развивались быстрее, чем изменялись версии средств цифровой подписи, направленного шифрования и распределение ключей.

Функции (продолжение(2) Основным методом защиты стали изменения параметров, в смысле их увеличения, например, модулей преобразования. Так, в Эль-Гамаля и DSA системах длина модуля преобразования составляет порядка 1024 и более битов. Но при этом до такой же длины были увеличены длины ключей, как следствие увеличилась вычислительная сложность криптографических преобразований и уменьшилась скорость. В тоже время все преобразования необходимо осуществлять все с возрастающими скоростями, как правило, в реальном масштабе времени. Разрешение указанного противоречия было найдено за счет реализации различных несимметричных преобразований в группах точек эллиптических кривых. К настоящему времени, уже разработаны, прошли сертификацию и утверждены несколько стандартов цифровой подписи на эллиптических кривых. Прежде всего, это международный стандарт цифровой подписи Х 9. 62 -1998. В 2001 году в России так же был введен новый стандарт на цифровые подписи основанный на эллиптических кривых - ГОСТ Р 34. 10 -2001. o Основными преимуществами этих стандартов является возможность уменьшения в 5 и более раз длин ключей и общесистемных параметров, большая степень увеличения сложности криптоанализа с ростом размеров общесистемных параметров, а также уменьшение вычислительной мощности всех преобразований. Все это и предопределило переход, а по существу перевод, существующих алгоритмов цифровой подписи на вычисления в группах точек эллиптических кривых. o

Список литературы: o 1. Коржев В. Цифровая подпись. Эллиптические кривые. «Открытые системы» (8 августа 2002). o 2. D. Brown Generic groups, collision resistance, and ECDSA. «Codes and Cryptography» (26 февраля 2002).
Презентация1.ppt