Основы зонной теории полупроводников 1 Немного о квантовой

Основы зонной теории полупроводников 1. Немного о квантовой физике. • Волны как частицы: фотоны и фононы. • Частицы как волны: соотношение неопределенностей. • Атом водорода. Квантование энергии и момента количества движения. • Принцип Паули. Периодическая система элементов Д. И. Менделеева.

Основы зонной теории полупроводников 2. Движение электронов в идеальном кристалле • Простая картина уширения атомных уровней в зоны разрешенных энергий • Уравнение Шредингера. Основные приближения. Теорема Блоха. Квазиимпульс. Зона Бриллюэна. • Методы сильно и слабо связанных электронов. Энергетические зоны. • Закон дисперсии. Изоэнергетические поверхности. Тензор обратной эффективной массы. Плотность состояний. • Зонная структура некоторых полупроводников: Ge, Si, Ga. As

Основы зонной теории полупроводников 3. Движение электронов во внешних полях. Неидеальные кристаллы (с примесями) • Метод эффективной массы. • Энергетические зоны в электрическом поле. • Движение электронов и дырок в магнитном поле. Определение эффективных масс из циклотронного (диамагнитного) резонанса. • Уровни энергии, создаваемые примесными центрами в полупроводниках. Доноры и акцепторы. Водородоподобные примесные центры. Глубокие примесные уровни.

Кацусика Хокусай. Большая волна в Канагава. Из серии «Тридцать шесть видов Фудзи»

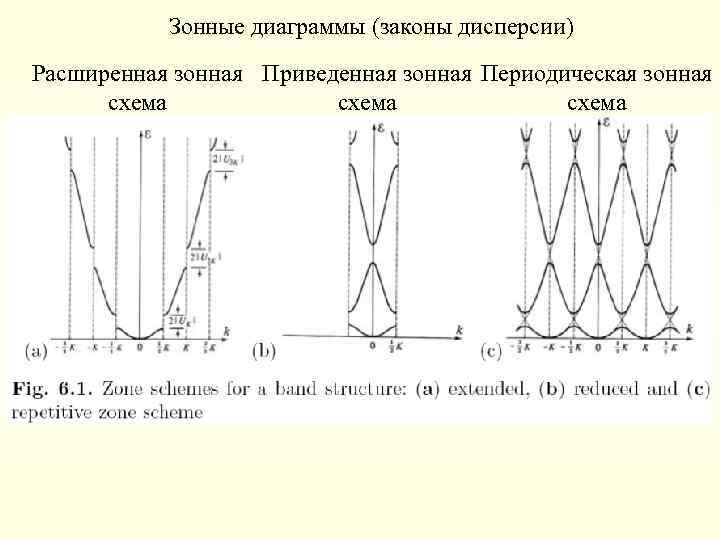Зонные диаграммы (законы дисперсии) Расширенная зонная Приведенная зонная Периодическая зонная схема

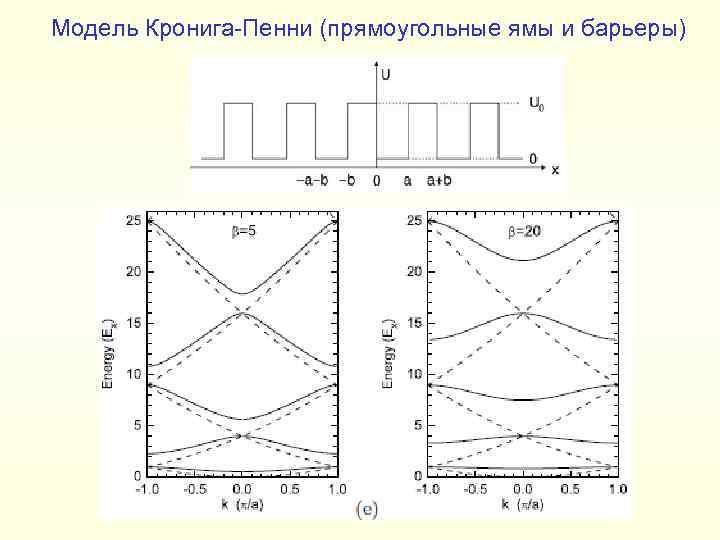Модель Кронига-Пенни (прямоугольные ямы и барьеры)

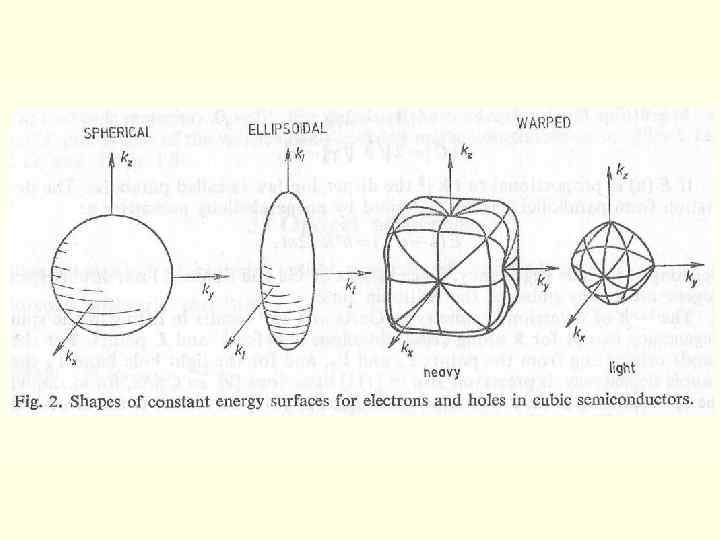
Изоэнергетические поверхности для электронов

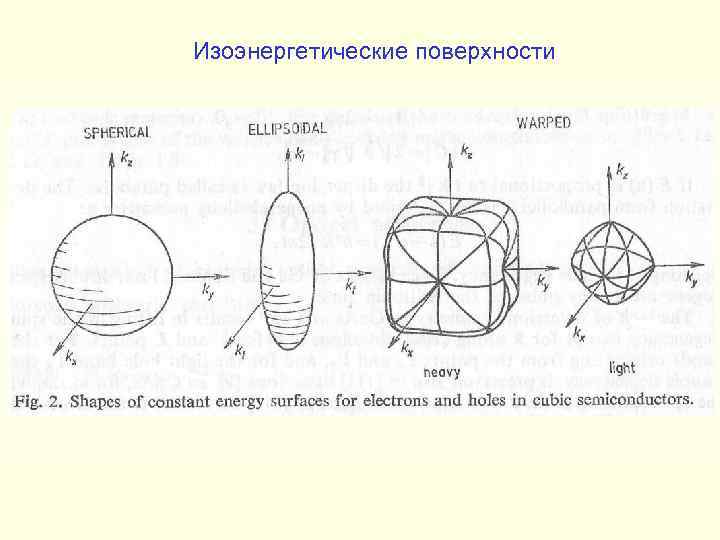Изоэнергетические поверхности

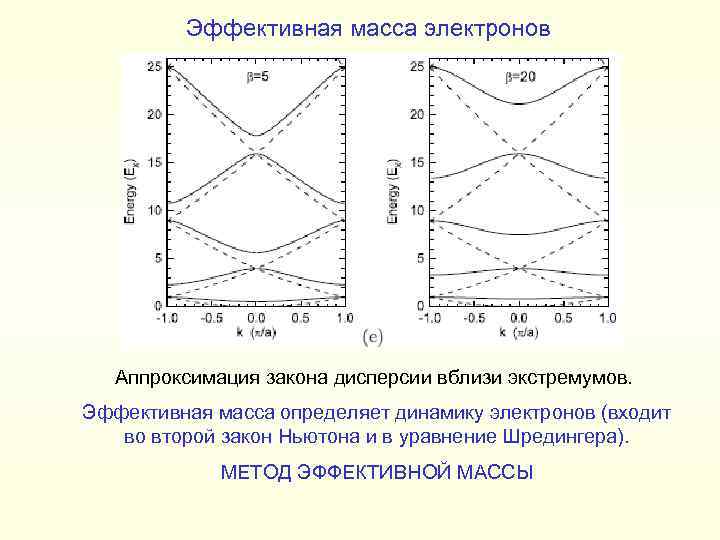Эффективная масса электронов Аппроксимация закона дисперсии вблизи экстремумов. Эффективная масса определяет динамику электронов (входит во второй закон Ньютона и в уравнение Шредингера). МЕТОД ЭФФЕКТИВНОЙ МАССЫ

Свободный электрон Состояние Энергия Скорость Уравнение движения Закон сохранения импульса при столкновениях Электрон в кристалле (j – номер зоны)

Электроны и дырки Дырка: заполненная валентная зона с одним пустым местом Чем глубже дырка в валентной зоне, тем больше энергия системы электронов валентной зоны (то есть дырки) Масса дырки положительна и равна модулю массы электрона Заряд дырки положителен (это следует из закона сохранения заряда при рождении пары электрон-дырка) Квазиимпульс дырки противоположен квазиимпульсу, указывающему на пустое место

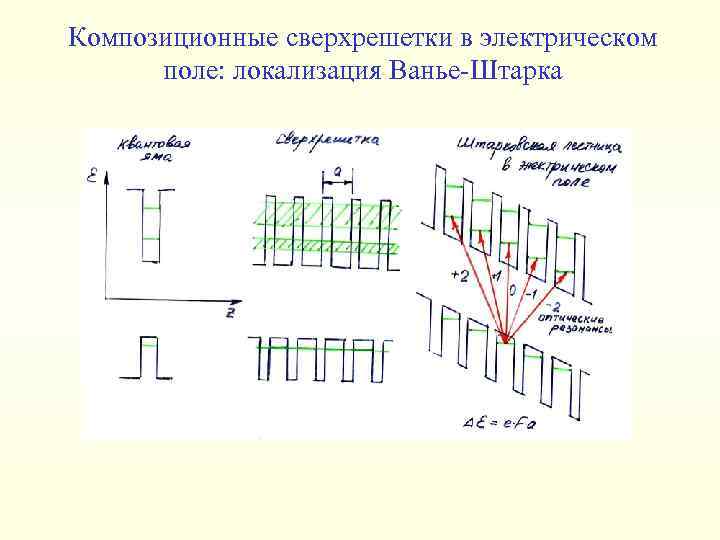Композиционные сверхрешетки в электрическом поле: локализация Ванье-Штарка

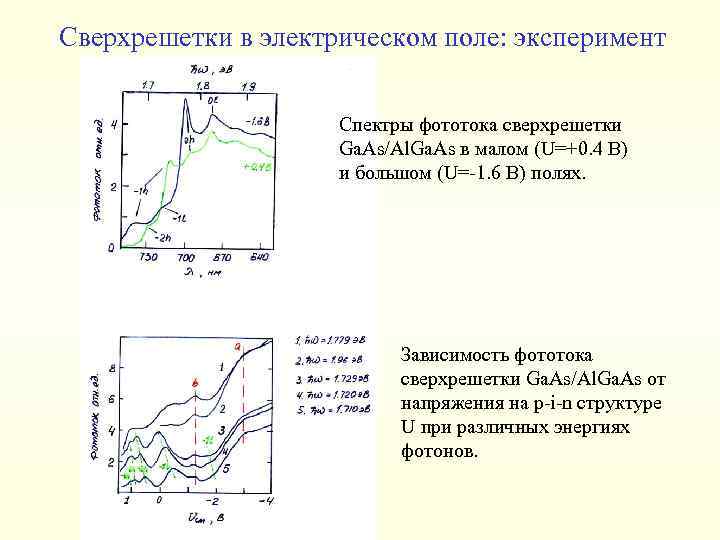Cверхрешетки в электрическом поле: эксперимент Спектры фототока сверхрешетки Ga. As/Al. Ga. As в малом (U=+0. 4 В) и большом (U=-1. 6 В) полях. Зависимость фототока сверхрешетки Ga. As/Al. Ga. As от напряжения на p-i-n структуре U при различных энергиях фотонов.

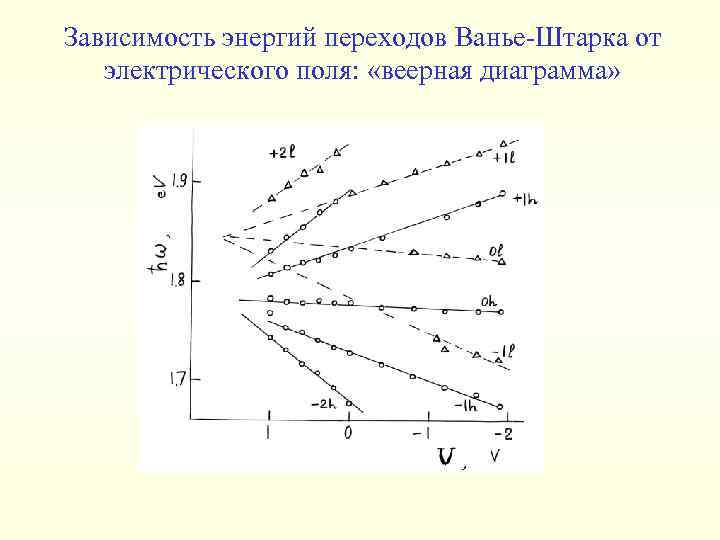Зависимость энергий переходов Ванье-Штарка от электрического поля: «веерная диаграмма»

Движение электронов и дырок в магнитном поле В магнитном поле H под действием силы Лоренца электроны двигаются по круговым орбитам с циклотронной частотой с: Уравнение движения электрона в поле электромагнитной волны и магнитном поле Н : Столкновения с частотой 1/ Поле волны Сила Лоренца

Циклотронный резонанс Определение Резонансное поглощение электромагнитной волны с частотой, близкой к циклотронной, полупроводником с газом свободных электронов, помещенным в магнитное поле Объяснение Циркулярно-поляризованная волна с с, находящаяся в фазе с циклотронным вращением электронов, «раскручивает» электронные орбиты. Условие наблюдения циклотронного резонанса – редкие столкновения электронов с примесями или фононами (частота столкновений много меньше циклотронной частоты:

Энергетический спектр электронов в квантующем поле: g-фактор: g=2 для электронов в вакууме; g=-0. 44 в Ga. As

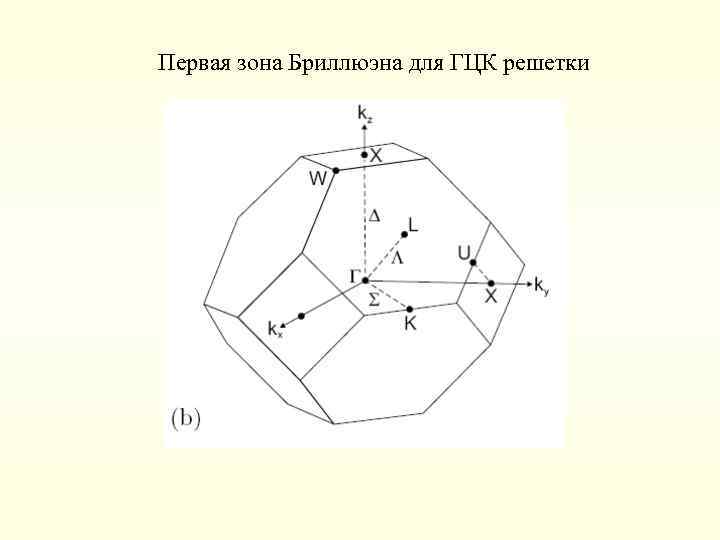Первая зона Бриллюэна для ГЦК решетки

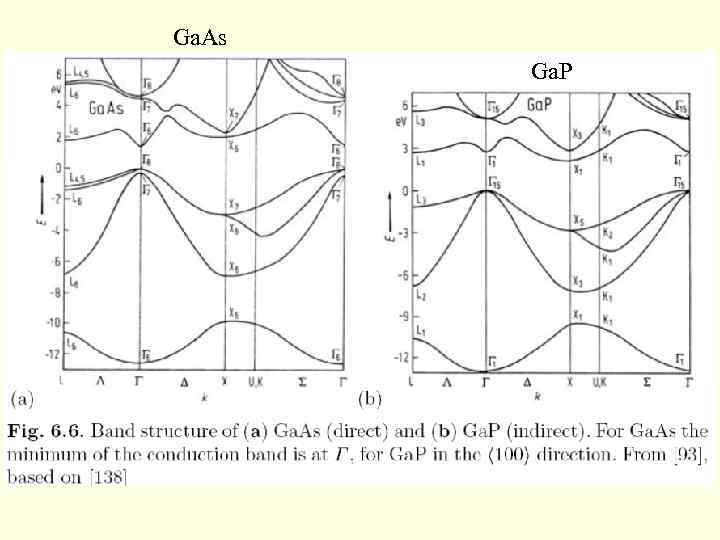Ga. As Ga. P

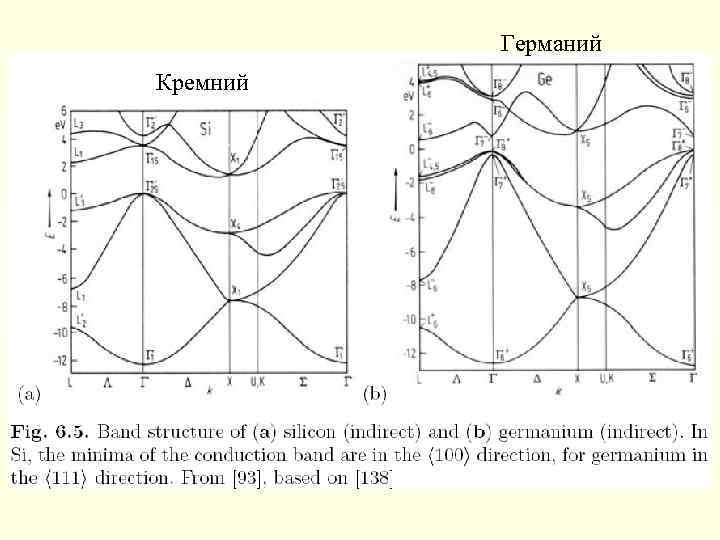Германий Кремний

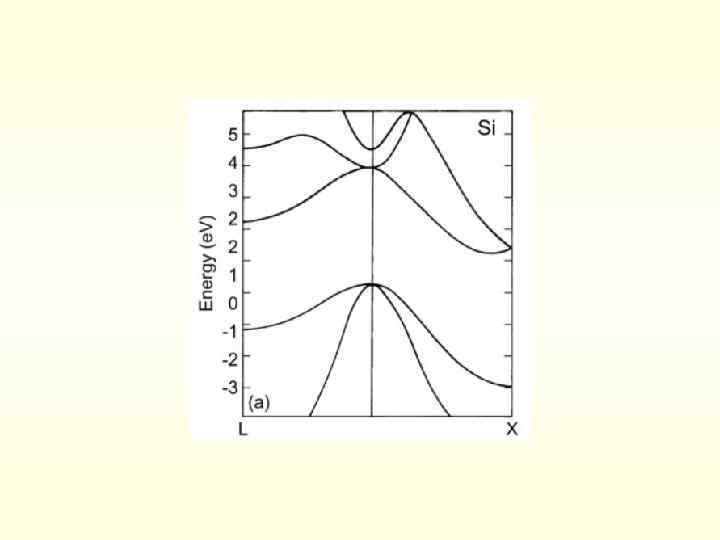
Изоэнергетические поверхности для электронов

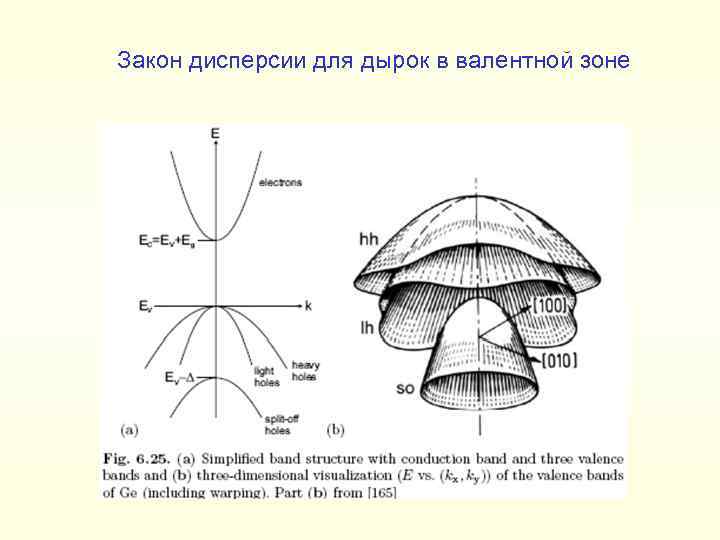Закон дисперсии для дырок в валентной зоне

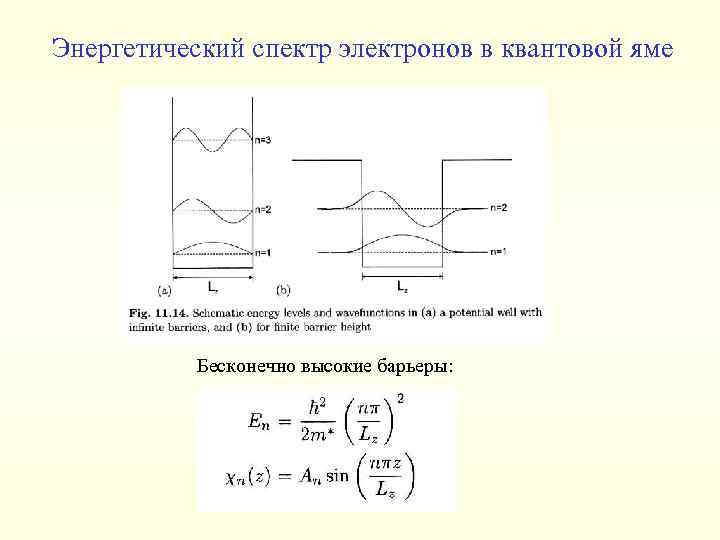Энергетический спектр электронов в квантовой яме Бесконечно высокие барьеры:

Распределение квантовых состояний в зонах. Плотность состояний. Разрешенные состояния квазиволнового вектора k определяются из граничных условий на волновую функцию электронов. Условие периодичности волновой функции на границах куба с длиной ребра L (условия Кармана-Борна): Объём в зоне Бриллюэна, приходящийся на каждое состояние: Число квантовых состояний в элементе d 3 p (на единицу объёма):

Законы дисперсии для дырок в валентной зоне