Скачать презентацию Основы управления финансовыми активами Показатели оценки финансовых Скачать презентацию Основы управления финансовыми активами Показатели оценки финансовых

Modul_6.ppt

  • Количество слайдов: 56

Основы управления финансовыми активами Основы управления финансовыми активами

Показатели оценки финансовых активов Показатели оценки финансовых активов

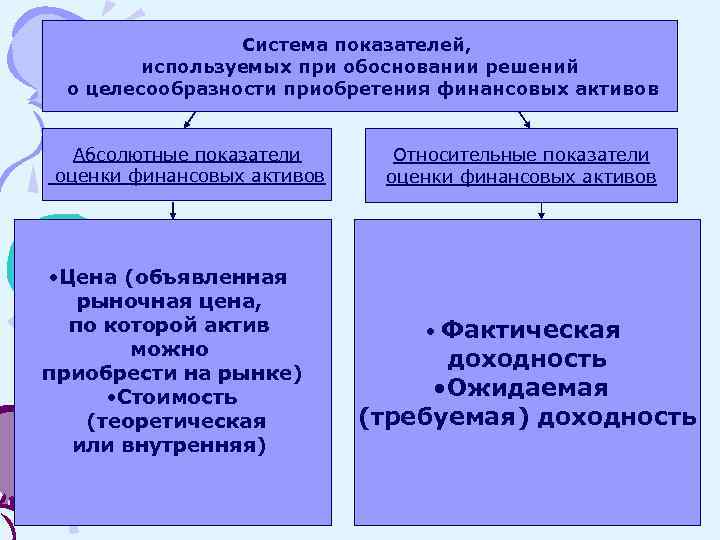Система показателей, используемых при обосновании решений о целесообразности приобретения финансовых активов Абсолютные показатели оценки Система показателей, используемых при обосновании решений о целесообразности приобретения финансовых активов Абсолютные показатели оценки финансовых активов • Цена (объявленная рыночная цена, по которой актив можно приобрести на рынке) • Стоимость (теоретическая или внутренняя) Относительные показатели оценки финансовых активов Фактическая доходность • Ожидаемая (требуемая) доходность •

Цена и стоимость изменяются в динамике и с позиции конкретного инвестора могут не совпадать. Цена и стоимость изменяются в динамике и с позиции конкретного инвестора могут не совпадать. Цена объективна, объявлена, товар (ценная бумага) по ней равнодоступен, в любой конкретный момент времени она однозначна. Стоимость не определена и субъективна: каждый инвестор имеет свой собственный взгляд на внутреннюю стоимость актива. Число оценок зависит от числа профессиональных участников.

Соотношения между ценой и стоимостью • Цена больше стоимости Рыночная цена финансового актива завышена Соотношения между ценой и стоимостью • Цена больше стоимости Рыночная цена финансового актива завышена и нет необходимости его покупать • Цена меньше стоимости Цена финансового актива занижена и покупка по этой цене выгодна • Цена равна стоимости Рыночная цена полностью соответствует внутренней стоимости, и нет возможности спекулировать на операциях с ценными бумагами

В основе оценки ценных бумаг лежит фундаменталистская теория: оценка финансовых активов производится на основе В основе оценки ценных бумаг лежит фундаменталистская теория: оценка финансовых активов производится на основе будущих поступлений.

Модели оценки стоимости финансовых активов. Принятие решений на основе показателя стоимости финансовых активов Модели оценки стоимости финансовых активов. Принятие решений на основе показателя стоимости финансовых активов

Базовая модель оценки стоимости финансовых активов (DCF - модель) CFt - ожидаемый денежный поток Базовая модель оценки стоимости финансовых активов (DCF - модель) CFt - ожидаемый денежный поток в i– м периоде; r- приемлемая (ожидаемая или требуемая) доходность; t– горизонт прогнозирования. Формула предполагает капитализацию дохода с доходностью, равной ставке дисконтирования. Для разных инвесторов Vo может иметь разные значения , т. к. по – разному оцениваются поступления денежных средств и приемлемая норма доходности. С использованием модели решаются задачи расчета текущей стоимости актива и расчета нормы прибыли для сравнения с приемлемым ее значением для инвестора.

Приемлемая норма доходности (r) может быть принята: • В размере ставки процента по банковскому Приемлемая норма доходности (r) может быть принята: • В размере ставки процента по банковскому депозиту • Ставки процента, выплачиваемого по вкладам, плюс надбавка за риск • В виде процента, выплачиваемого по государственным ценным бумагам, плюс надбавка за риск

Модификации базовой модели оценки финансовых активов Модификации базовой модели оценки финансовых активов

Модели оценки облигаций Модели оценки облигаций

Оценка облигаций с нулевым купоном (поступления денежных средств по годам, за исключением последнего, равны Оценка облигаций с нулевым купоном (поступления денежных средств по годам, за исключением последнего, равны нулю) Vo – стоимость облигации с позиции инвестора (теоретическая стоимость); CF - сумма, выплачиваемая при погашении облигации; n- число лет, через которое произойдет погашение облигации; I - доход в абсолютном выражении; N - номинальная стоимость

Оценка бессрочных облигаций (долговая выплата производится в установленном проценте или по плавающей ставке) СF Оценка бессрочных облигаций (долговая выплата производится в установленном проценте или по плавающей ставке) СF – ежегодная сумма дохода, выплачиваемая по облигации; d - требуемая доходность инвестируемого капитала.

Оценка безотзывных облигаций с постоянным доходом (денежный поток складывается из одинаковых по годам поступлений Оценка безотзывных облигаций с постоянным доходом (денежный поток складывается из одинаковых по годам поступлений C и нарицательной стоимости в момент погашения) При годовом начислении процентов

Оценка безотзывных облигаций с постоянным доходом (денежный поток складывается из одинаковых по годам поступлений Оценка безотзывных облигаций с постоянным доходом (денежный поток складывается из одинаковых по годам поступлений C и нарицательной стоимости в момент погашения) При полугодовом начислении процентов Ik – годовой купонный доход; N – нарицательная стоимость, выплачиваемая при погашении облигации; d- требуемая доходность инвестируемого капитала; n- число лет до погашения облигаций; k- число раз начисления процентов

Оценка отзывных облигаций с постоянным доходом Производится по формулам оценки безотзывных облигаций с постоянным Оценка отзывных облигаций с постоянным доходом Производится по формулам оценки безотзывных облигаций с постоянным доходом при годовом или полугодовом начислении процентов, в которых нарицательная стоимость N заменена выкупной ценой Pm

Модели оценки стоимости акций Модели оценки стоимости акций

Оценка стоимости акции, используемой в течение заранее неопределенного срока Va - внутренняя или теоретическая Оценка стоимости акции, используемой в течение заранее неопределенного срока Va - внутренняя или теоретическая стоимость акции с позиции инвестора, выполняющего анализ (субъективная оценка инвестором ожидаемого потока и рискованность акции); D - сумма дивидендов, предполагаемая к получению в каждом n периоде; ds - текущая требуемая доходность; n- число периодов включенных в расчет.

Оценка стоимости акции, используемой в течение заранее определенного срока D - сумма дивидендов, предполагаемая Оценка стоимости акции, используемой в течение заранее определенного срока D - сумма дивидендов, предполагаемая к получению в каждом n периоде; Pm - ожидаемая курсовая стоимость акции в конце периода ее реализации; ds- текущая требуемая доходность; n- число периодов включенных в расчет.

Оценка стоимости акций со стабильным уровнем дивиденда Va - текущая цена привилегированной акции; D- Оценка стоимости акций со стабильным уровнем дивиденда Va - текущая цена привилегированной акции; D- ожидаемый фиксированный дивиденд; ds - текущая требуемая доходность.

Оценка стоимости акций с равномерно возрастающим дивидендом (доходы корпорации также равномерно увеличиваются; доля прибыли, Оценка стоимости акций с равномерно возрастающим дивидендом (доходы корпорации также равномерно увеличиваются; доля прибыли, выплачиваемая в виде дивидендов, остается постоянной) Va - внутренняя или теоретическая стоимость акции с позиции инвестора, выполняющего анализ (субъективная оценка инвестором ожидаемого потока и рискованность акции); D 1 – дивиденд, ожидаемый к получению (D 1= D 0*(1+g), где D 0 – последний фактически выплаченный дивиденд); ds- требуемая доходность акции, учитывающая как риск, так и доходность альтернативных вариантов инвестирования; g- предполагаемый темп прироста дивиденда.

Оценка стоимости акций с равномерно возрастающим дивидендом в случае поквартальной выплаты дивидендов Dgt – Оценка стоимости акций с равномерно возрастающим дивидендом в случае поквартальной выплаты дивидендов Dgt – дивиденд в квартале t; ds - требуемая эффективная годовая ставка; g – годовой темп прироста дивиденда.

Оценка стоимости акций с изменяющимся темпом прироста дивиденда n - ожидаемое число лет непостоянного Оценка стоимости акций с изменяющимся темпом прироста дивиденда n - ожидаемое число лет непостоянного роста; Dt – ожидаемый дивиденд в году t фазы непостоянного роста; Dn+1 – первый ожидаемый дивиденд фазы постоянного роста; ds – требуемая доходность акции; g- ожидаемый темп прироста, когда компания достигает стабильности.

Доходность финансового актива Доходность финансового актива

Доходность финансового актива относительный показатель, характеризующий эффективность использования финансовых активов. Показатели доходности используются для Доходность финансового актива относительный показатель, характеризующий эффективность использования финансовых активов. Показатели доходности используются для обоснования решений о целесообразности приобретения акций и облигаций.

Исходная формула расчета доходности d - доход, генерируемый активом (дивиденд, процент, прирост капитализированной стоимости); Исходная формула расчета доходности d - доход, генерируемый активом (дивиденд, процент, прирост капитализированной стоимости); I – регулярный доход от использования актива, полученный в виде процентов или дивидендов; CI - величина инвестиций в актив.

Виды показателей доходности • Фактическая доходность – Рассчитывается на основе фактически полученных данных и Виды показателей доходности • Фактическая доходность – Рассчитывается на основе фактически полученных данных и имеет значение лишь для ретроспективного анализа • Ожидаемая доходность – рассчитывается на основе прогнозных данных в рамках имитационного перспективного анализа и используется для принятия решения о целесообразности приобретения тех или иных ценных бумаг.

Алгоритм расчета доходности актива или dt - общая доходность; ds – текущая доходность; dc Алгоритм расчета доходности актива или dt - общая доходность; ds – текущая доходность; dc – капитализированная доходность; P 0 - цена приобретения актива; Pm – ожидаемая цена реализации актива; I - регулярный доход от использования актива, полученный в виде процентов или дивидендов.

Доходность облигаций Доходность облигаций

Доходность облигации без права досрочного погашения (YTM), или доходность к погашению (используется в сравнительном Доходность облигации без права досрочного погашения (YTM), или доходность к погашению (используется в сравнительном анализе при выборе вариантов инвестирования) N – номинал облигации; P 0 – текущая цена (на момент оценки); Ik – купонный доход; t - число лет, оставшихся до погашения облигации.

При сравнении доходности YTM облигаций с различной частотой начисле 6 ния процентов – годовое, При сравнении доходности YTM облигаций с различной частотой начисле 6 ния процентов – годовое, квартальное, ежемесячное – необходим о перейти от номинальной ставки (dn ) к эффективной (de ). Формула расчета эффективной ставки: dn -номинальная годовая процентная ставка (доходность); de -эффективная годовая процентная ставка; m-количество начислений процентов в год

Доходность облигации с прав досрочного погашения (YTС) (используется для оценки доходности на момент отзыва Доходность облигации с прав досрочного погашения (YTС) (используется для оценки доходности на момент отзыва облигации с рынка или ее досрочного погашения ) Расчет YTC осуществляется на основе формулы оценки безотзывной облигации с постоянным доходом с выплатой процентов каждые полгода, в которой номинал заменен выкупной ценой Pm.

Доходность акций Доходность акций

Доходность бессрочной привилегированной акции D – ожидаемый дивиденд; P 0 - текущая рыночная цена Доходность бессрочной привилегированной акции D – ожидаемый дивиденд; P 0 - текущая рыночная цена акции.

Доходность (ожидаемая) обыкновенной акции с равномерно возрастающим дивидендом D 1 - ожидаемый дивиденд (D Доходность (ожидаемая) обыкновенной акции с равномерно возрастающим дивидендом D 1 - ожидаемый дивиденд (D 1 = D 0 (1 + g), где D 0 - последний полученный к моменту оценки дивиденд по акции ); P 0 - цена акции на момент оценки; g- темп прироста дивиденда.

Принимая решение, финансовый менеджер должен сначала оценить рискованность инвестиций, а затем опреде 6 лять, Принимая решение, финансовый менеджер должен сначала оценить рискованность инвестиций, а затем опреде 6 лять, является ли уровень доходности достаточным для компенсации ожидаемого риска.

Оценка риска финансовых активов Оценка риска финансовых активов

Рисокванность актива степень вариабельности дохода (или доходности), который может быть получен благодаря владению данным Рисокванность актива степень вариабельности дохода (или доходности), который может быть получен благодаря владению данным активом.

Измерение риска финансовых активов Используются статистические коэффициенты: • Размах вариации • Дисперсия • Среднеквадратическое Измерение риска финансовых активов Используются статистические коэффициенты: • Размах вариации • Дисперсия • Среднеквадратическое (стандартное) отклонение • Коэффициент вариации Особенности применения статистических коэффициентов: • Результативность операций с финансовыми активами принято измерять не доходом, а доходностью • Основными показателями оценки риска на рынке капиталов являются дисперсия и среднеквадратическое отклонение • На финансовом рынке большинство величин, представляющих интерес для инвесторов, оцениваются в вероятностных терминах

Риск актива – величина непостоянная и зависит, в частности, от того, в каком контексте Риск актива – величина непостоянная и зависит, в частности, от того, в каком контексте рассматривается данный актив – изолированно или как составная часть инвестиционного портфеля.

Алгоритм оценки риска альтернативных вариантов инвестиций в предположении, что каждый из них рассматривается изолированно Алгоритм оценки риска альтернативных вариантов инвестиций в предположении, что каждый из них рассматривается изолированно от общего риска в вероятностных терминах

1. Делаются прогнозные оценки значений доходности (di ) и вероятностей их осуществления (pi ). 1. Делаются прогнозные оценки значений доходности (di ) и вероятностей их осуществления (pi ).

2. Рассчитывается наиболее вероятная доходность (dml ): 2. Рассчитывается наиболее вероятная доходность (dml ):

3. Рассчитывается среднеквадратическое (стандартное) отклонение (σ ): 3. Рассчитывается среднеквадратическое (стандартное) отклонение (σ ):

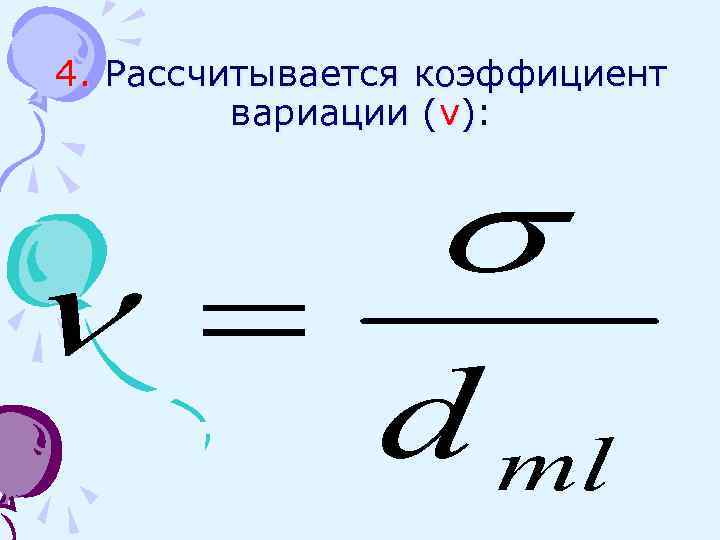4. Рассчитывается коэффициент вариации (ν): 4. Рассчитывается коэффициент вариации (ν):

● Коэффициент вариации является наиболее предпочтительной мерой в сравнительном анализе общего риска ряда активов. ● Коэффициент вариации является наиболее предпочтительной мерой в сравнительном анализе общего риска ряда активов. ● Чем дальше горизонт планирования, тем труднее предсказать доходность актива, т. е. размах вариации доходности, равно как и коэффициент вариации, увеличивается. Чем более долговременным является данный вид актива, тем он более рискован, тем большая вариация доходности с ним связана. ● При объединении активов в портфели релевантным является рыночный риск, который представляет собой долю риска данного актива в риске портфеля в целом. ● Общий риск актива включает в себя специфический для компании (диверсифицируемый) риск, который можно устранить с помощью диверсификации, и рыночный риск, который нельзя устранить диверсификацией.

При оценке портфеля и целесообразности операций с входящими в него активами необходимо оперировать показателями При оценке портфеля и целесообразности операций с входящими в него активами необходимо оперировать показателями доходности и риска портфеля в целом.

Ожидаемая доходность портфеля (dp ) Линейная функция показателей доходности входящих в него активов, или Ожидаемая доходность портфеля (dp ) Линейная функция показателей доходности входящих в него активов, или средневзвешенная доходность отдельных активов.

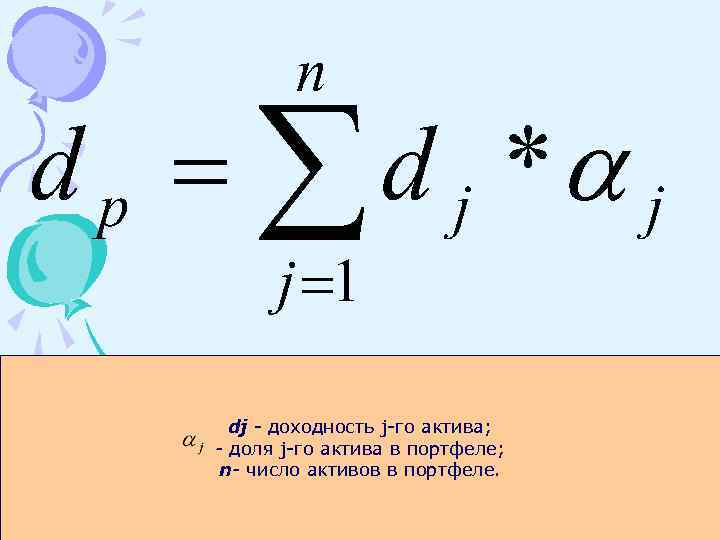dj - доходность j-го актива; - доля j-го актива в портфеле; n- число активов dj - доходность j-го актива; - доля j-го актива в портфеле; n- число активов в портфеле.

Мера риска портфелясреднеквадратическое отклонение - доля i-го актива в портфеле; σi- вариация доходности i-го Мера риска портфелясреднеквадратическое отклонение - доля i-го актива в портфеле; σi- вариация доходности i-го актива; Kij - коэффициент корреляции между ожидаемыми доходностями i-го и j-го активов.

● среднеквадратическое отклонение портфеля ≠ средневзвешенной из среднеквадратических отклонений отдельных активов, его составляющих. ● ● среднеквадратическое отклонение портфеля ≠ средневзвешенной из среднеквадратических отклонений отдельных активов, его составляющих. ● объединение активов в портфель снижает риск портфеля в целом. ● эффективный портфель – портфель, который обеспечивает набольшую доходность при данном уровне риска или наименьший риск при данной доходности. Эффективный портфель сочетает рисковые и безрисковые активы.

Принципы формирования портфеля инвестиций (теория инвестиционного портфеля У. Шарпа и Г. Марковица) • Успех Принципы формирования портфеля инвестиций (теория инвестиционного портфеля У. Шарпа и Г. Марковица) • Успех инвестиций в основном зависит от правильного распределения средств по типам активов • Риск инвестиций в определенный тип ценных бумаг определяется вероятностью отклонения прибыли от ожидаемого значения • Общая доходность и риск инвестиционного портфеля могут меняться путем варьирования его структуры • Все оценки, используемые при составлении инвестиционного портфеля, носят вероятностный характер.

Конструирование рынка в соответствии с требованиями классической теории возможно лишь при наличии ряда факторов: Конструирование рынка в соответствии с требованиями классической теории возможно лишь при наличии ряда факторов: • Сформировавшегося рынка ценных бумаг • Определенного периода его функционирования • Статистики рынка

Модель оценки доходности финансовых активов (CAPM) Модель оценки доходности финансовых активов (CAPM)

Модель оценки доходности финансовых активов (описывает зависимость между рыночным риском и доходностью отдельно взятой Модель оценки доходности финансовых активов (описывает зависимость между рыночным риском и доходностью отдельно взятой ценной бумаги): de- ожидаемая доходность акций данной компании; drf- доходность безрисковых ценных бумаг; dm- ожидаемая доходность в среднем на рынке ценных бумаг; β-коэффициент данной компании (измеряет рискованность ценной бумаги и характеризует изменчивость ее доходности относительно доходности рынка ценных бумаг или индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг); (dm- drf)- рыночная премия за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпораций); (de- drf) –премия за риск вложения капитала в ценные бумаги именно данной компании.

Модель CAPM позволяет: 1 ответить на вопрос, какой должна быть величина доходности, необходимая для Модель CAPM позволяет: 1 ответить на вопрос, какой должна быть величина доходности, необходимая для компенсации уровня риска 2 спрогнозировать доходность финансового актива 3 рассчитать теоретическую стоимость актива