Основы теории систем автоматического управления САУ 1

Основы теории систем автоматического управления (САУ)

1. Основные определения и понятия • Управление - целенаправленное воздействие на некоторый объект (автомобиль, станок, атомный реактор, фирму, завод…) • Автоматическое управление – управление без участия человека (чем проще объект управления, тем проще исключить человека)

Автоматизированное управление – управление с участием человека (чем сложнее объект управления, тем сложнее полностью исключить человека из процесса управления). Управление экономическими объектами как правило автоматизированное.

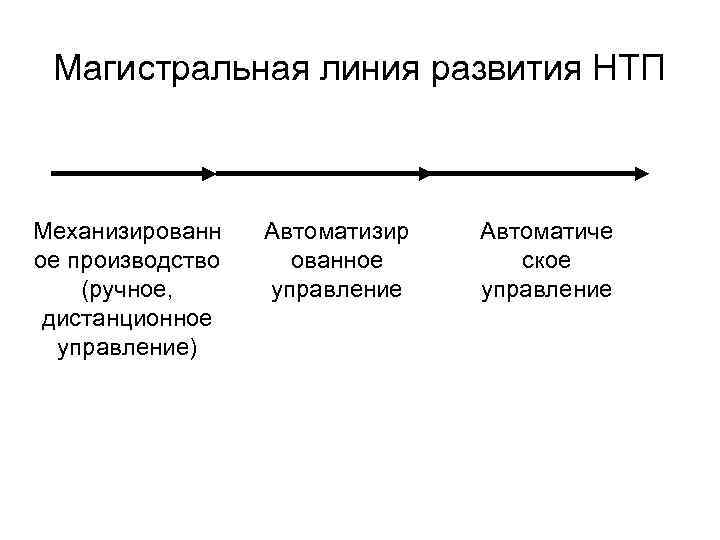Магистральная линия развития НТП Механизированн ое производство (ручное, дистанционное управление) Автоматизир ованное управление Автоматиче ское управление

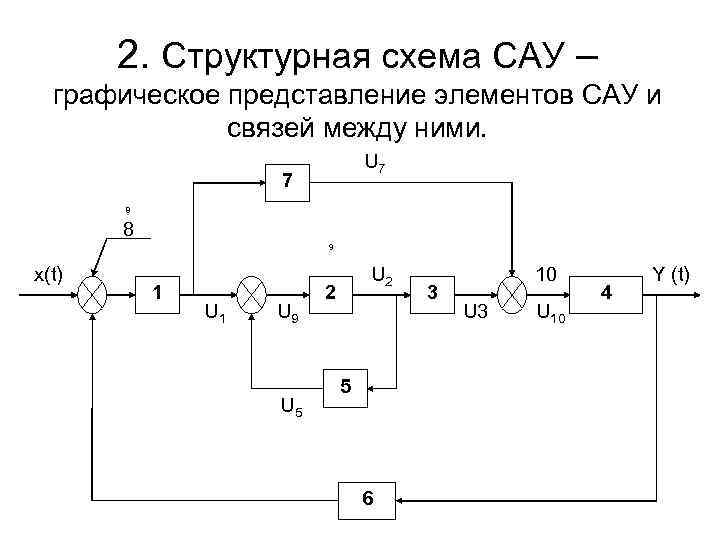2. Структурная схема САУ – графическое представление элементов САУ и связей между ними. U 7 7 8 8 9 x(t) 1 U 9 U 5 U 2 2 5 6 3 10 U 3 U 10 4 Y (t)

• 1 -7 - элементы САУ с их математическими моделями. • 8 -сравнивающий элемент (измеритель рассогласования) • ε (t) =X(t)-Y(t) • U 1 -U 10 - физические величины (напряжения, токи, силы, скорости, углы и т. п. ) Различают связи: • - прямые (через элемент 7) • - обратные местные (через элемент 5) • - обратная главная (через элемент 6)

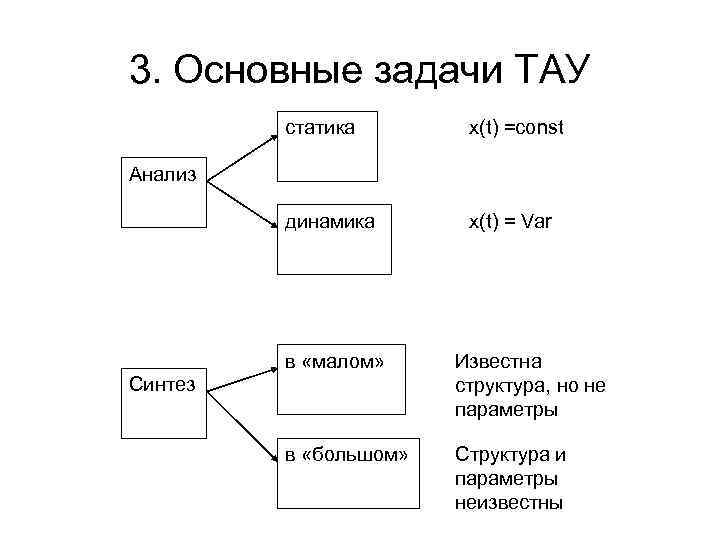3. Основные задачи ТАУ статика x(t) =const динамика x(t) = Var Анализ в «малом» Известна структура, но не параметры в «большом» Структура и параметры неизвестны Синтез

4. Преобразование по Лапласу – исключительно широко использовано в ТАУ. • Если X (t) - оригинал, • а X(s) – его изображение по Лапласу • и S - переменная Лапласа, то

5. Передаточная функция W(s) – элемента – это отношение преобразования по Лапласу от выходной величины к преобразованию по Лапласу от входной величины при нулевых начальных условиях: x(s) W(s) y(s) при нулевых начальных условиях

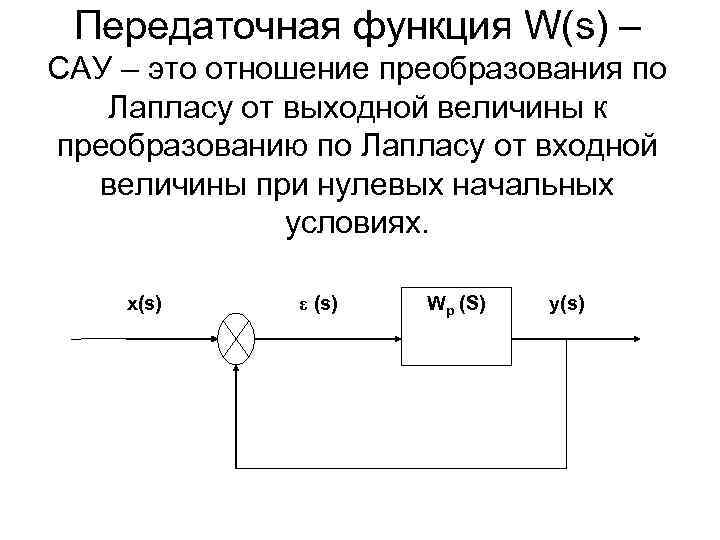Передаточная функция W(s) – САУ – это отношение преобразования по Лапласу от выходной величины к преобразованию по Лапласу от входной величины при нулевых начальных условиях. x(s) ε (s) Wp (S) y(s)

Различают W(s) САУ: • разомкнутой (при размыкании обратной связи): • замкнутой по входу-выходу:

• замкнутой по ошибке: В любых случаях понятие передаточной функции справедливо лишь при нулевых начальных условиях

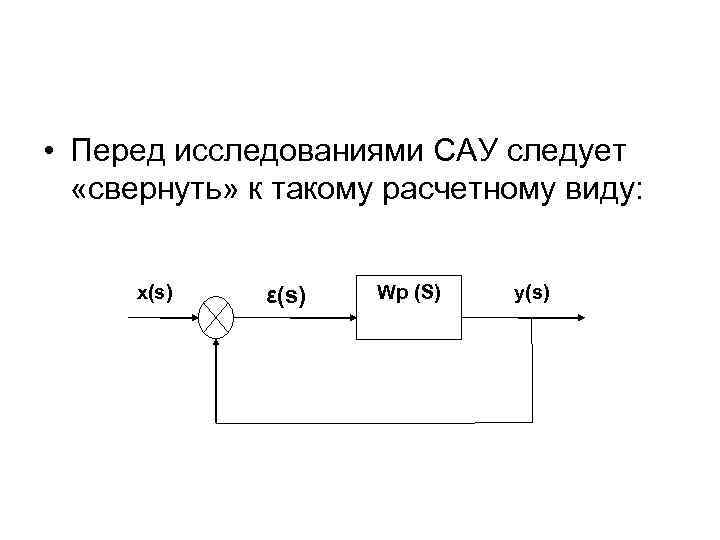• Перед исследованиями САУ следует «свернуть» к такому расчетному виду: x(s) ε(s) Wp (S) y(s)

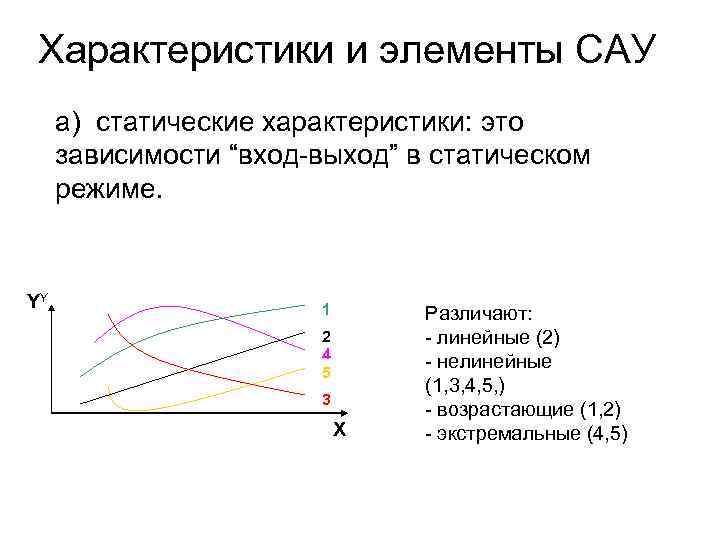Характеристики и элементы САУ а) статические характеристики: это зависимости “вход-выход” в статическом режиме. YY 1 2 4 5 3 X Различают: - линейные (2) - нелинейные (1, 3, 4, 5, ) - возрастающие (1, 2) - экстремальные (4, 5)

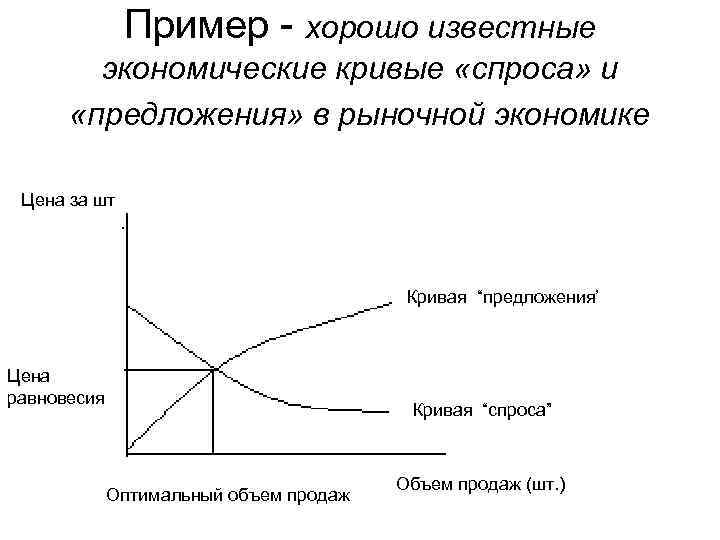Пример - хорошо известные экономические кривые «спроса» и «предложения» в рыночной экономике Цена за шт Кривая “предложения’ Цена равновесия Кривая “спроса” Оптимальный объем продаж Объем продаж (шт. )

б) Временные характеристики САУ – это реакции системы на типовые входные воздействия.

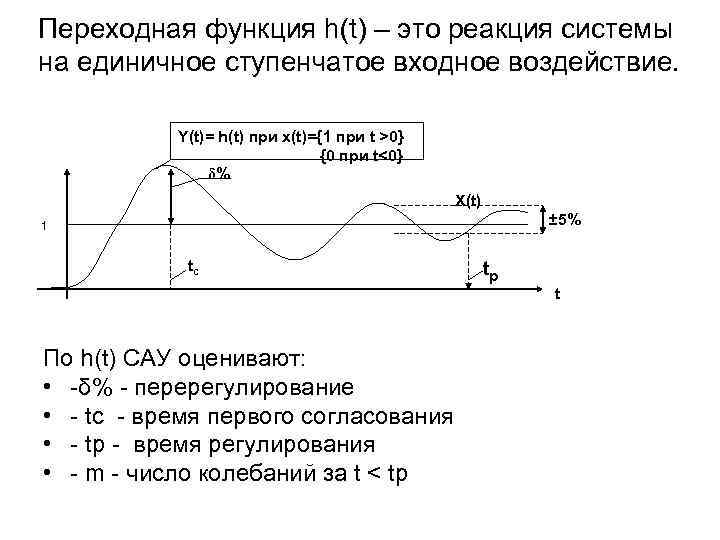Переходная функция h(t) – это реакция системы на единичное ступенчатое входное воздействие. Y(t)= h(t) при x(t)={1 при t >0} {0 при t<0} δ% X(t) ± 5% 1 tc tp t По h(t) САУ оценивают: • -δ% - перерегулирование • - tc - время первого согласования • - tp - время регулирования • - m - число колебаний за t < tp

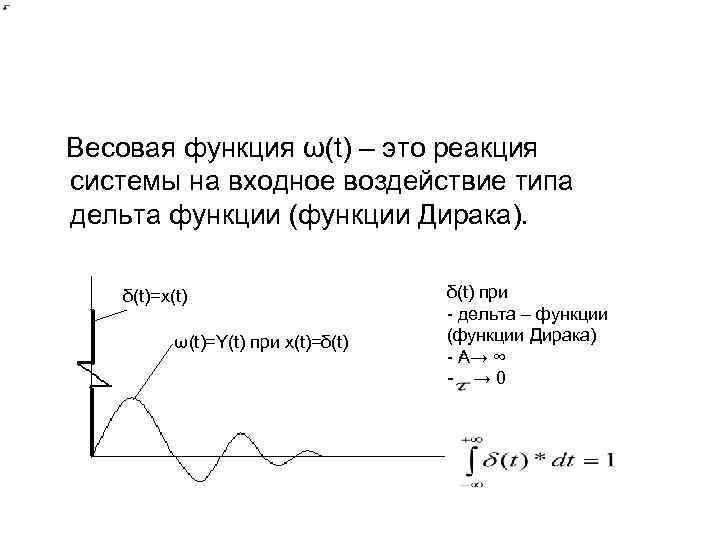Весовая функция ω(t) – это реакция системы на входное воздействие типа дельта функции (функции Дирака). δ(t)=x(t) ω(t)=Y(t) при x(t)=δ(t) при - дельта – функции (функции Дирака) - А→ ∞ - → 0

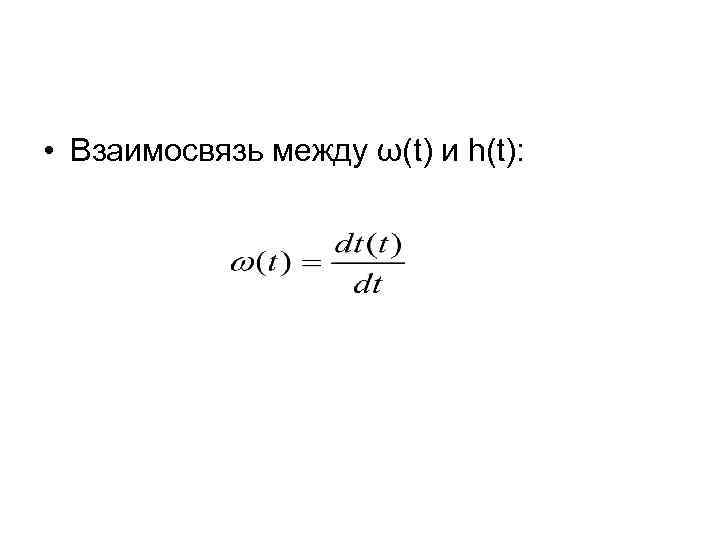• Взаимосвязь между ω(t) и h(t):

в) Частотные характеристики элементов и САУ • это формулы и графики показывающие прохождение гармонических сигналов через элементы и системы. Различают:

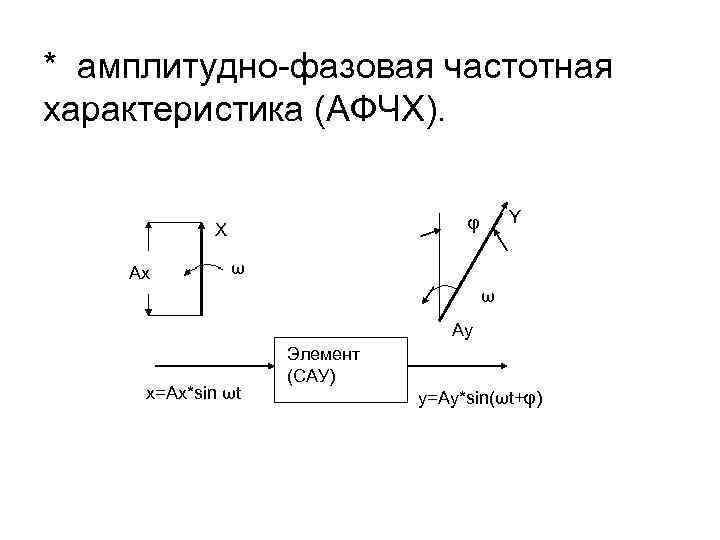* амплитудно-фазовая частотная характеристика (АФЧХ). Ах Y φ Х ω ω Ау х=Ах*sin ωt Элемент (САУ) y=Ay*sin(ωt+φ)

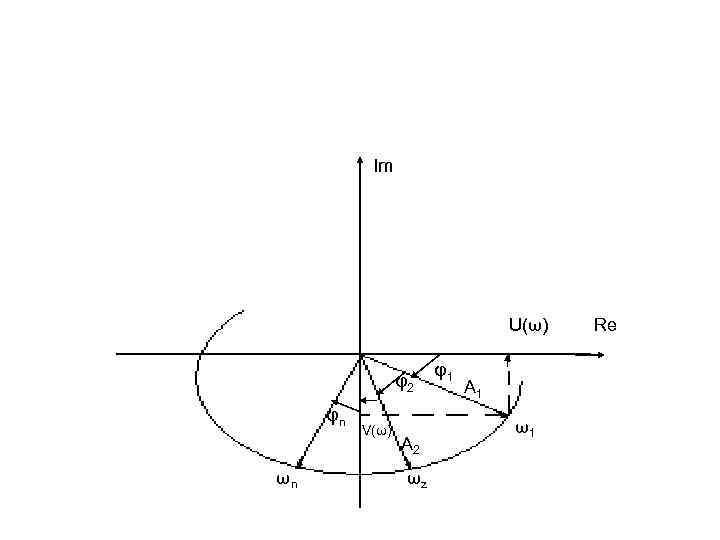Im U(ω) φ2 φn ωn V(ω) A 2 ωz φ1 A 1 ω1 Re

• АФЧХ – годограф описываемый на комплексной плоскости концом вектора с модулем: при изменении частоты 0<ω<∞, причем угол φ откладывается от вещественном положительной полуоси по часовой стрелке если он отрицателен и наоборот, иначе говоря. А(ω)е при 0<ω<∞ jφ(ω) = U(ω) + j. V(ω)

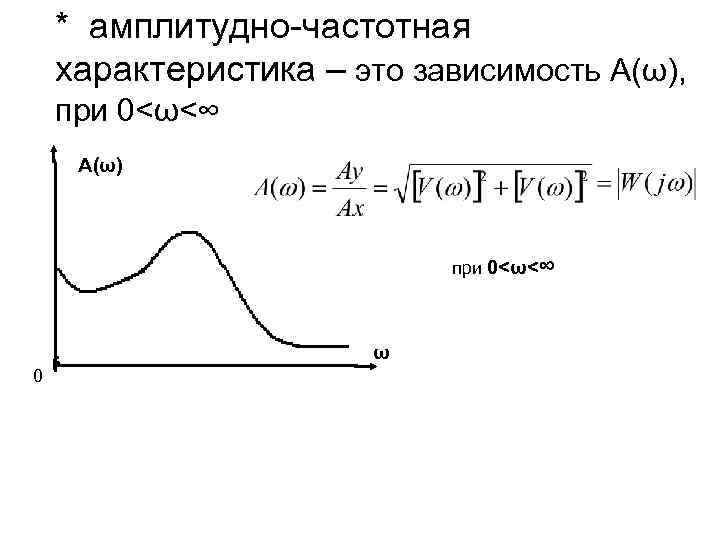* амплитудно-частотная характеристика – это зависимость А(ω), при 0<ω<∞ А(ω) при 0<ω<∞ ω 0

* фазо-частотная характеристика – это зависимость фазового сдвига φ(ω) между входным и выходным гармоническими сигналами элемента или системы при 0<ω<∞ φ(ω) 900 450 ω -450 -900

г) Логарифмические частотные характеристики – это формулы и графики, показывающие прохождение гармонических сигналов через элементы и системы, но в логарифмическом масштабе, когда вдоль горизонтальной оси откладывается десятичные логарифмы частоты.

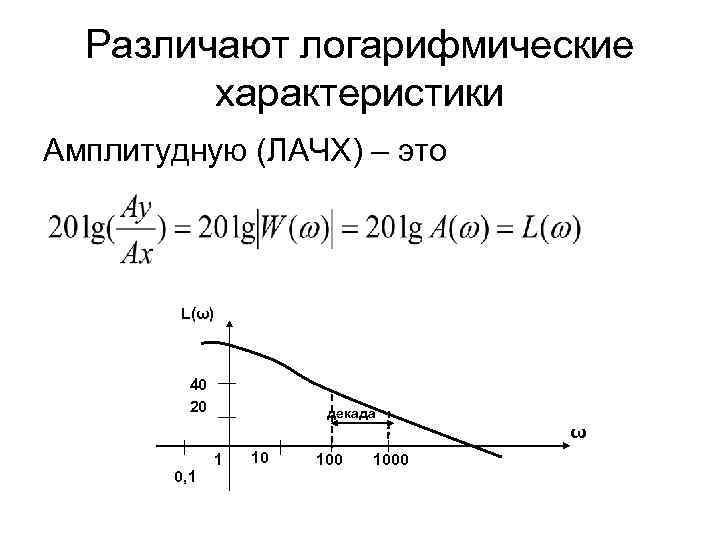Различают логарифмические характеристики Амплитудную (ЛАЧХ) – это L(ω) 40 20 декада ω 0, 1 1 10 1000

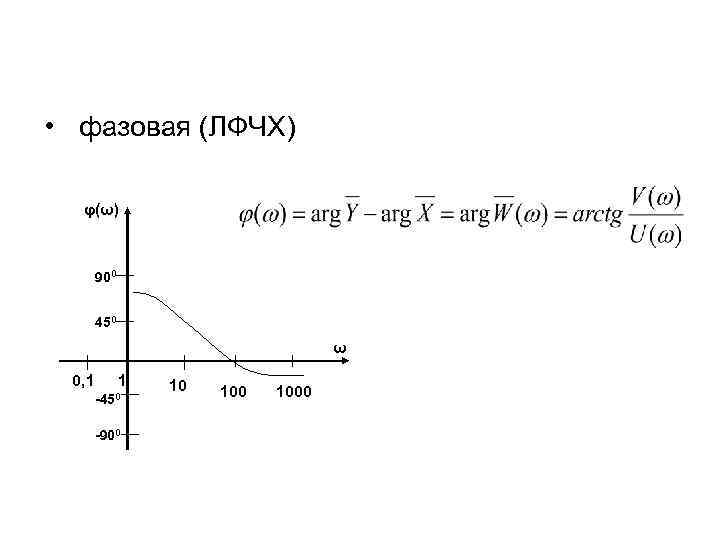• фазовая (ЛФЧХ) φ(ω) 900 450 ω 0, 1 1 -450 -900 10 1000

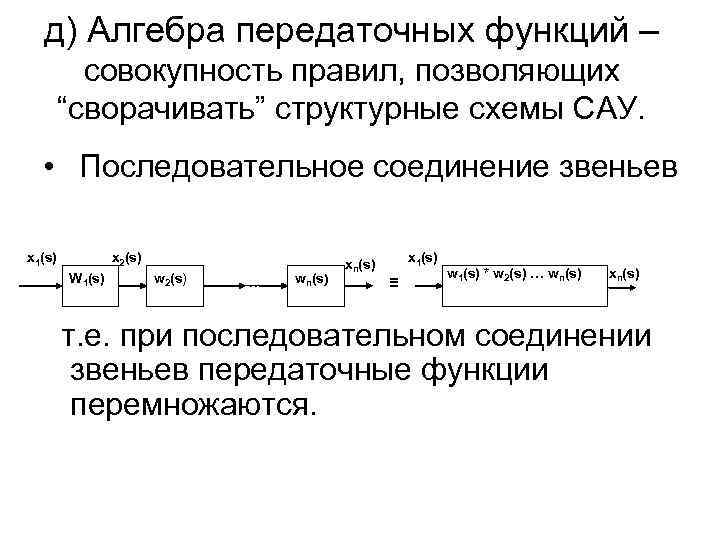д) Алгебра передаточных функций – совокупность правил, позволяющих “сворачивать” структурные схемы САУ. • Последовательное соединение звеньев x 2(s) x 1(s) W 1(s) w 2(s) … wn(s) x 1(s) ≡ w 1(s) * w 2(s) … wn(s) xn(s) т. е. при последовательном соединении звеньев передаточные функции перемножаются.

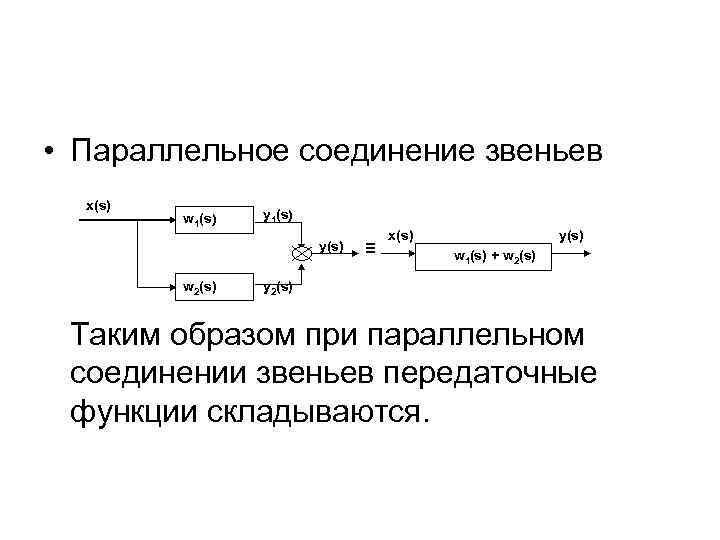• Параллельное соединение звеньев x(s) w 1(s) y(s) w 2(s) ≡ y(s) x(s) w 1(s) + w 2(s) y 2(s) Таким образом при параллельном соединении звеньев передаточные функции складываются.

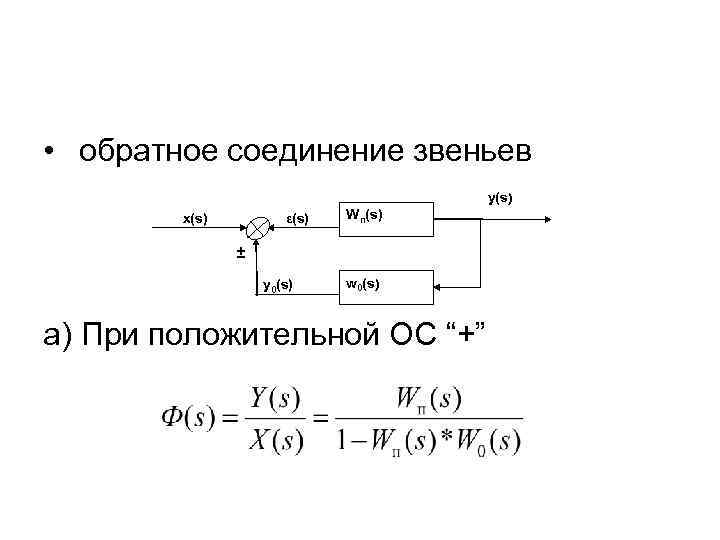• обратное соединение звеньев y(s) x(s) ε(s) Wп(s) ± y 0(s) w 0(s) a) При положительной ОС “+”

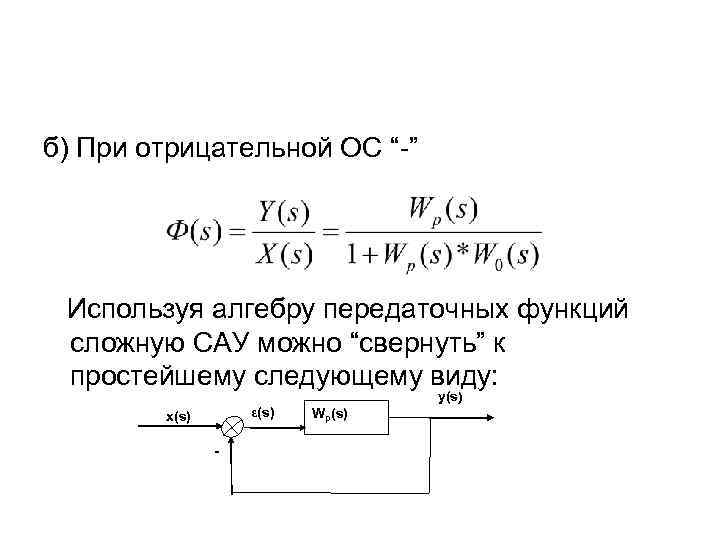б) При отрицательной ОС “-” Используя алгебру передаточных функций сложную САУ можно “свернуть” к простейшему следующему виду: y(s) ε(s) x(s) - Wр(s)

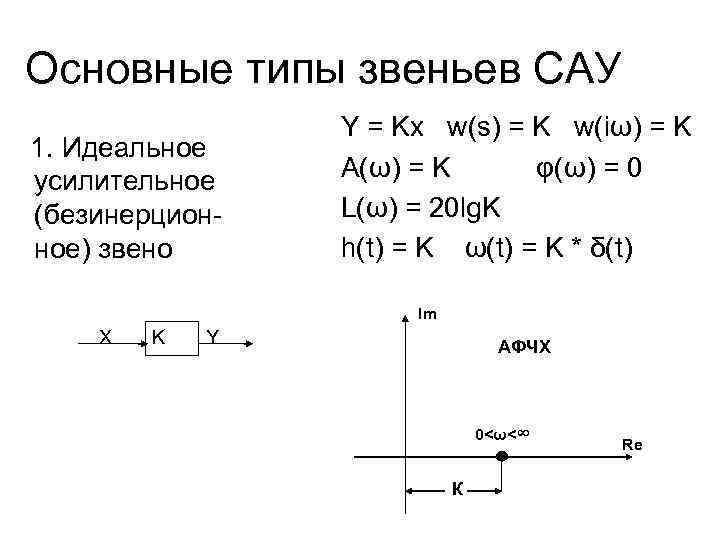Основные типы звеньев САУ 1. Идеальное усилительное (безинерционное) звено Y = Kx w(s) = K w(iω) = K A(ω) = K φ(ω) = 0 L(ω) = 20 lg. K h(t) = K ω(t) = K * δ(t) Im X K Y АФЧХ 0<ω<∞ К Re

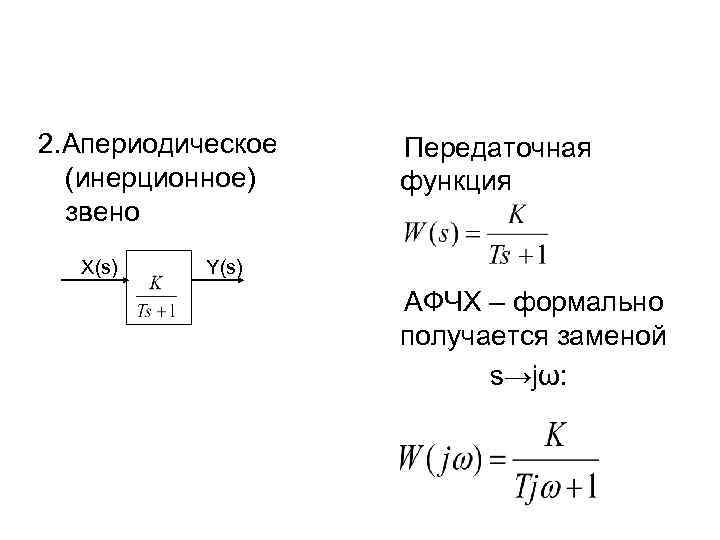2. Апериодическое (инерционное) звено X(s) Передаточная функция Y(s) АФЧХ – формально получается заменой s→jω:

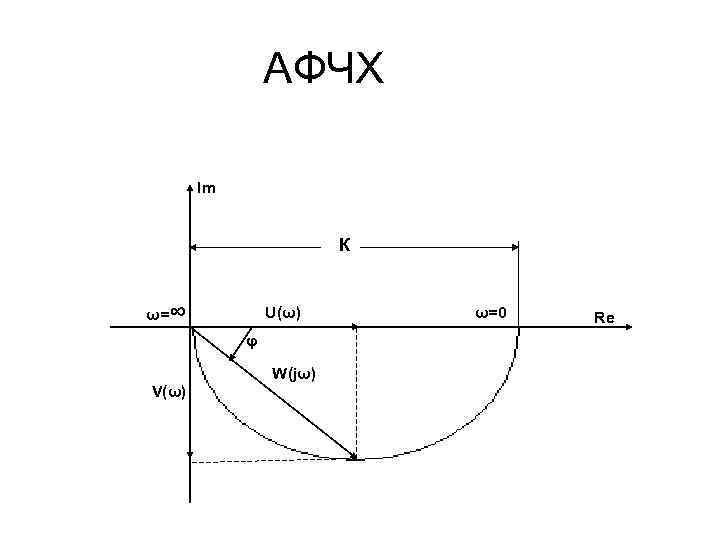АФЧХ Im К ω=∞ U(ω) φ W(jω) V(ω) ω=0 Re

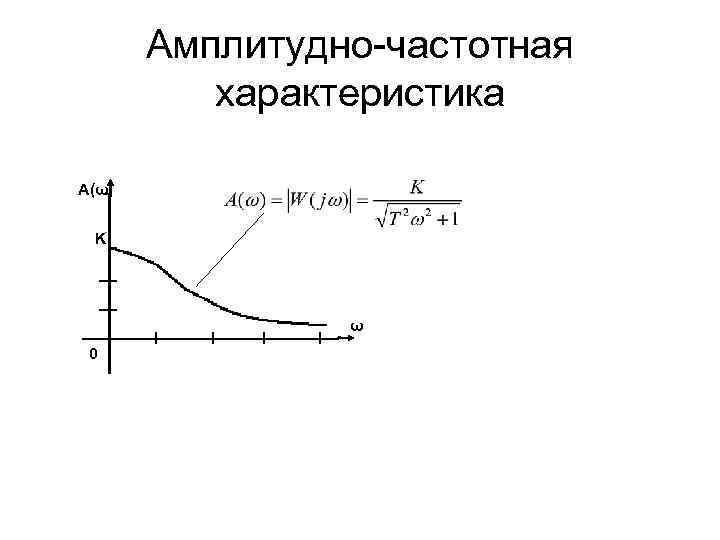Амплитудно-частотная характеристика A(ω) K ω 0

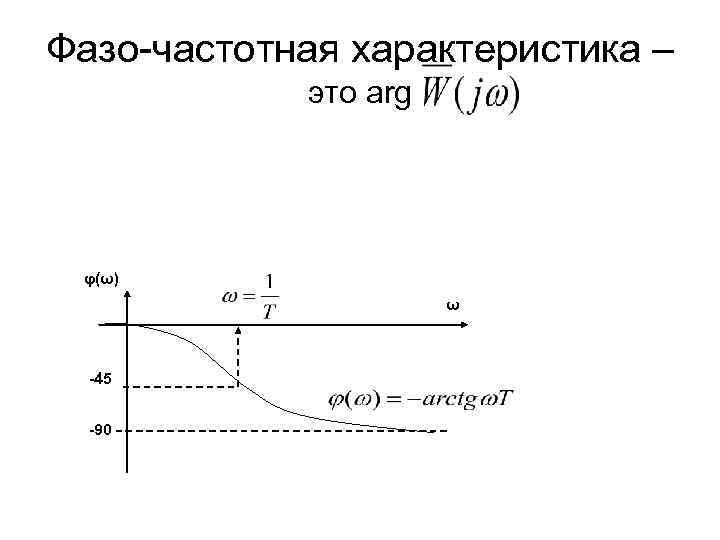Фазо-частотная характеристика – это arg φ(ω) ω -45 -90

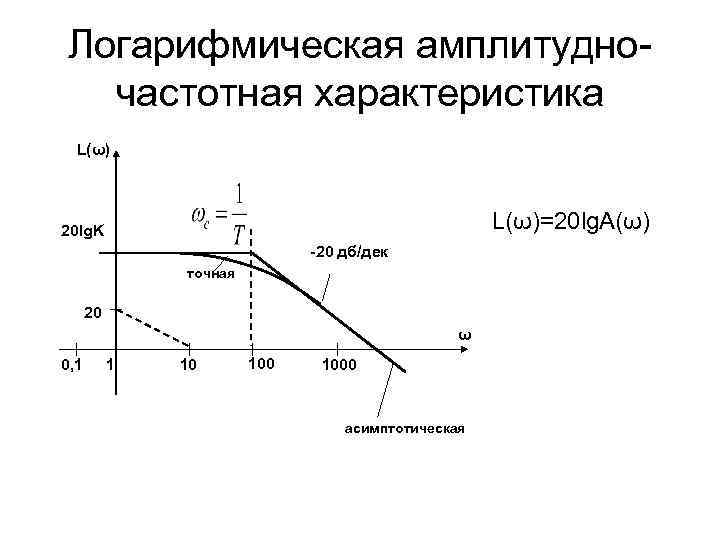Логарифмическая амплитудночастотная характеристика L(ω)=20 lg. A(ω) 20 lg. K -20 дб/дек точная 20 ω 0, 1 1 10 1000 асимптотическая

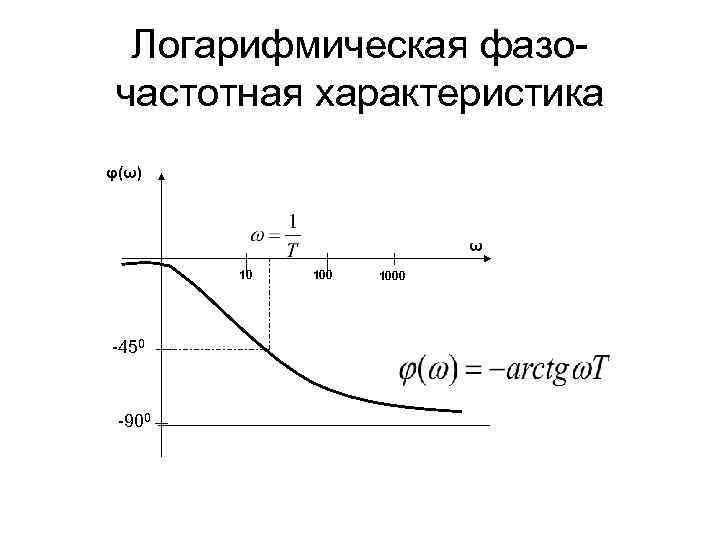Логарифмическая фазочастотная характеристика φ(ω) ω 10 -450 -900 1000

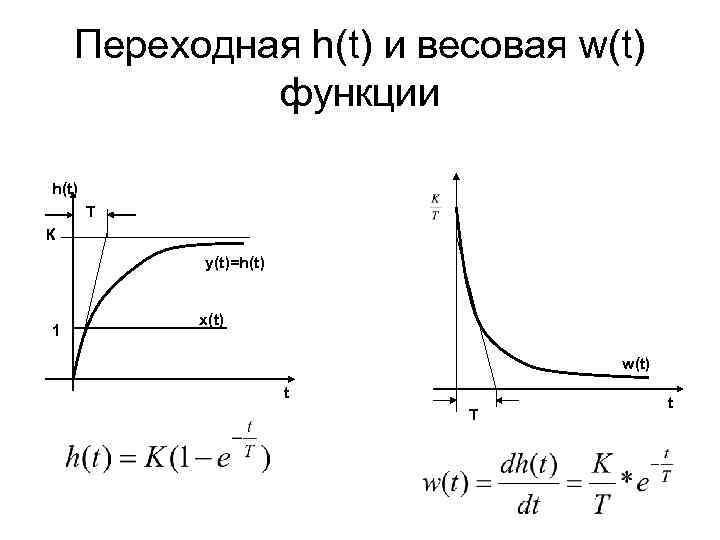Переходная h(t) и весовая w(t) функции h(t) Т К у(t)=h(t) 1 х(t) w(t) t Т t

3. Идеальное интегрирующее звено X Y

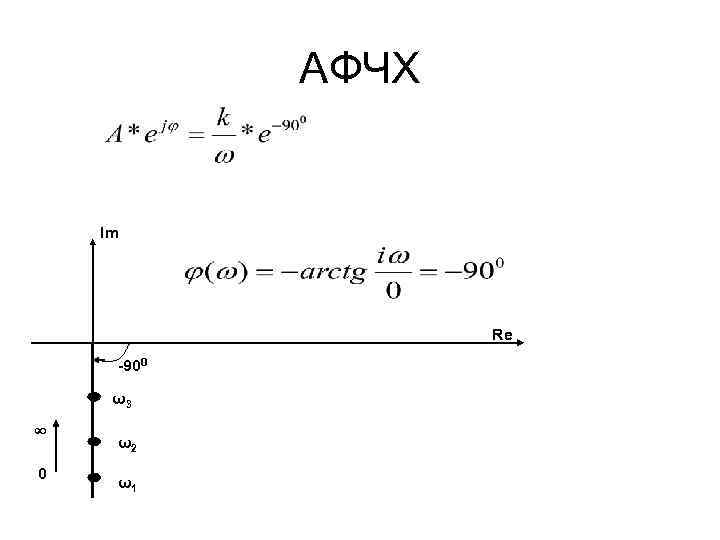АФЧХ Im Re -900 ω3 ∞ 0 ω2 ω1

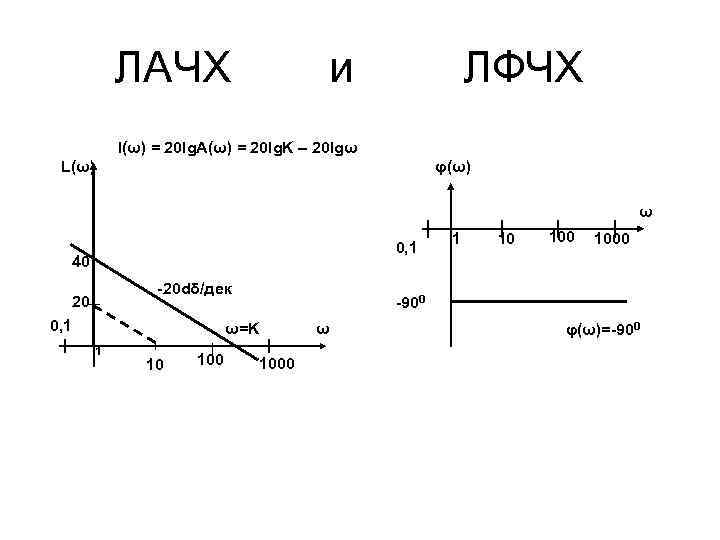ЛАЧХ и ЛФЧХ l(ω) = 20 lg. A(ω) = 20 lg. K – 20 lgω L(ω) φ(ω) ω 0, 1 40 -20 dδ/дек 20 0, 1 10 100 1000 -900 ω=K 1 1 1000 ω φ(ω)=-900

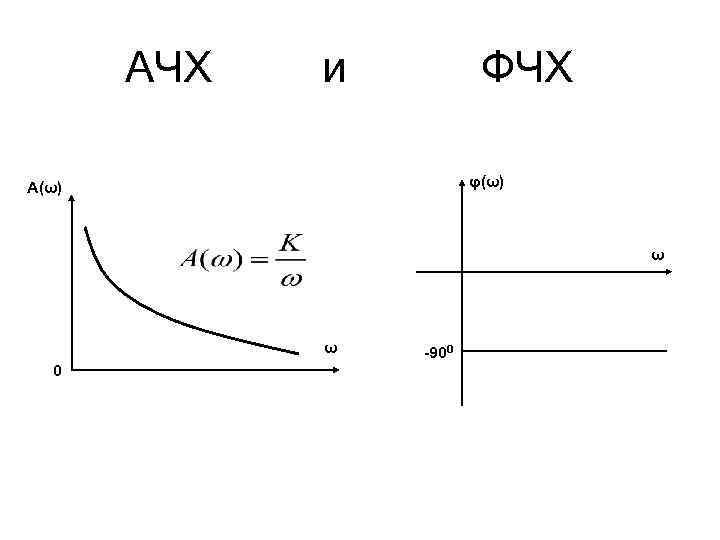АЧХ и ФЧХ φ(ω) A(ω) ω ω 0 -900

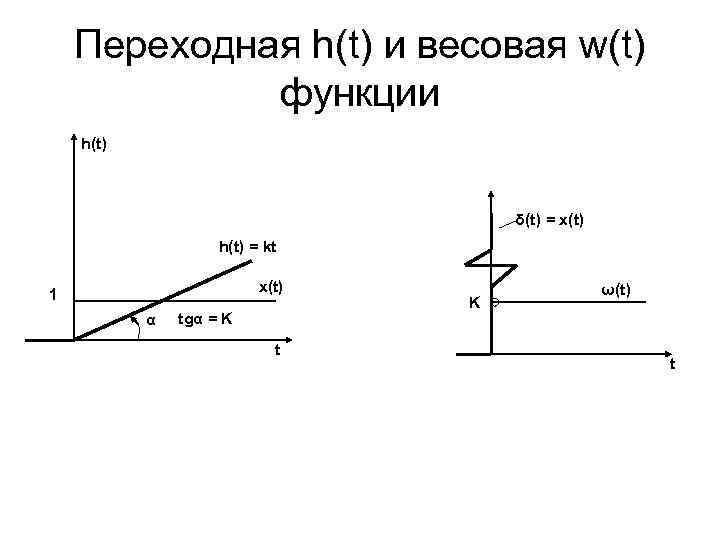Переходная h(t) и весовая w(t) функции h(t) δ(t) = x(t) h(t) = kt x(t) 1 α tgα = K t K ω(t) t

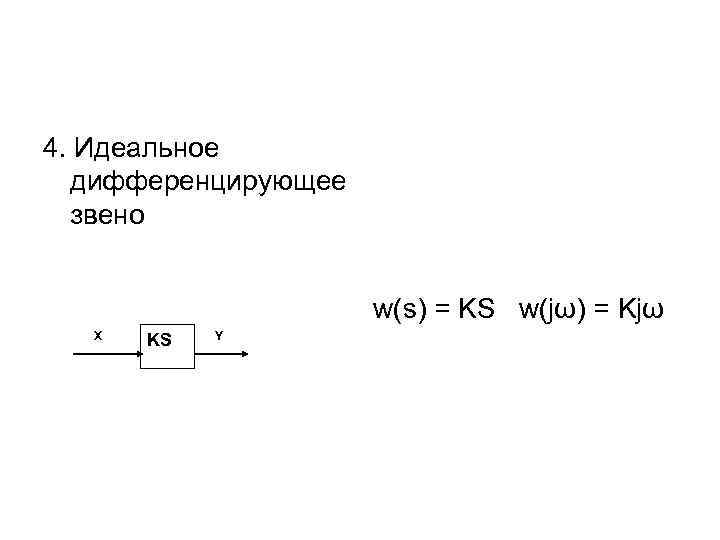4. Идеальное дифференцирующее звено w(s) = KS w(jω) = Kjω X KS Y

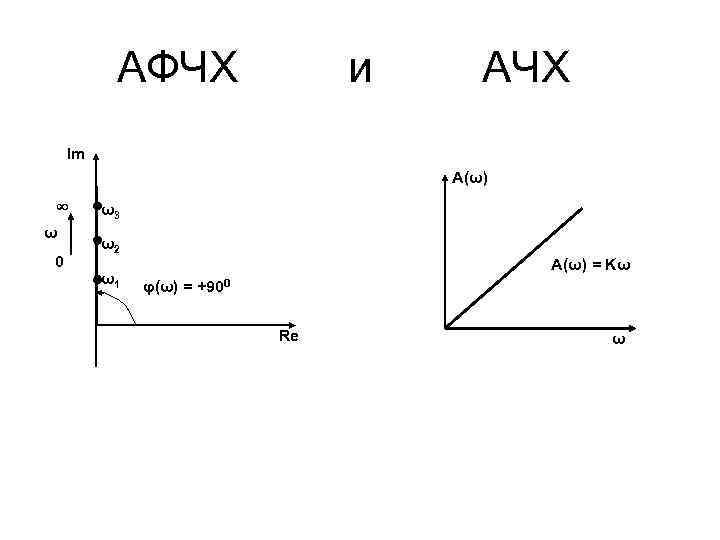АФЧХ и АЧХ Im A(ω) ∞ ω 0 ω3 ω2 ω1 A(ω) = Kω φ(ω) = +900 Re ω

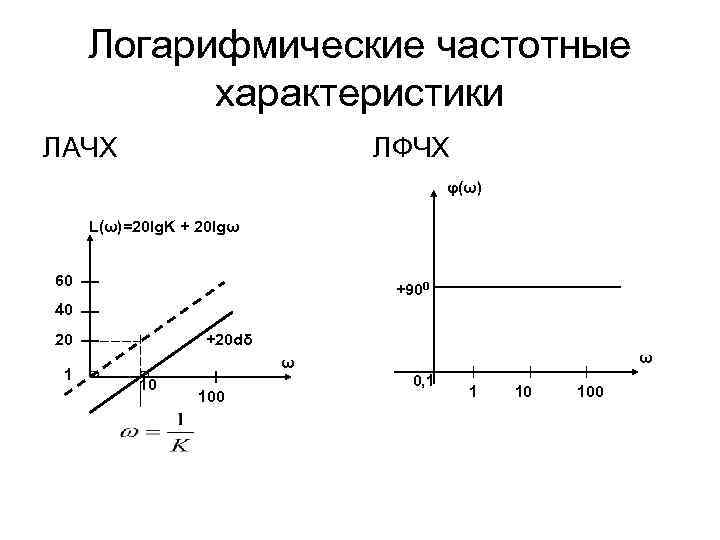Логарифмические частотные характеристики ЛАЧХ ЛФЧХ φ(ω) L(ω)=20 lg. K + 20 lgω 60 +900 40 20 1 +20 dδ ω 10 100 ω 0, 1 1 10 100

Правила преобразования структурных схем

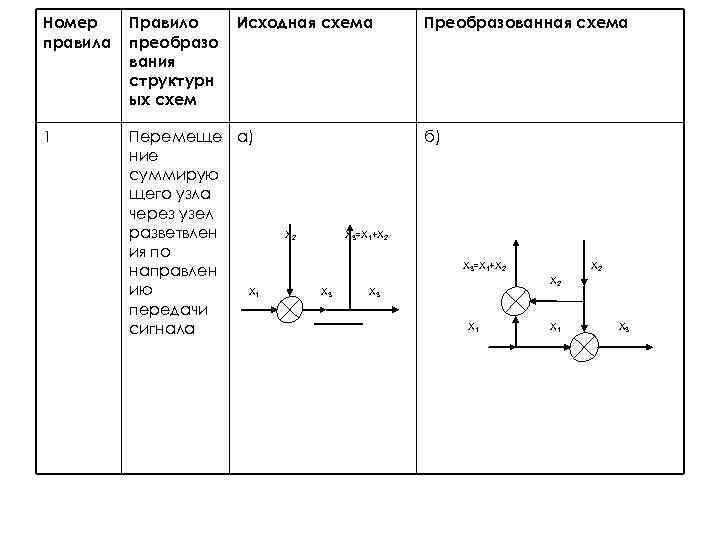Номер правила Правило преобразо вания структурн ых схем Исходная схема 1 Перемеще а) ние суммирую щего узла через узел разветвлен ия по направлен X 1 ию передачи сигнала Преобразованная схема б) X 3=X 1+X 2 X 3 X 2 X 3 X 1 X 3

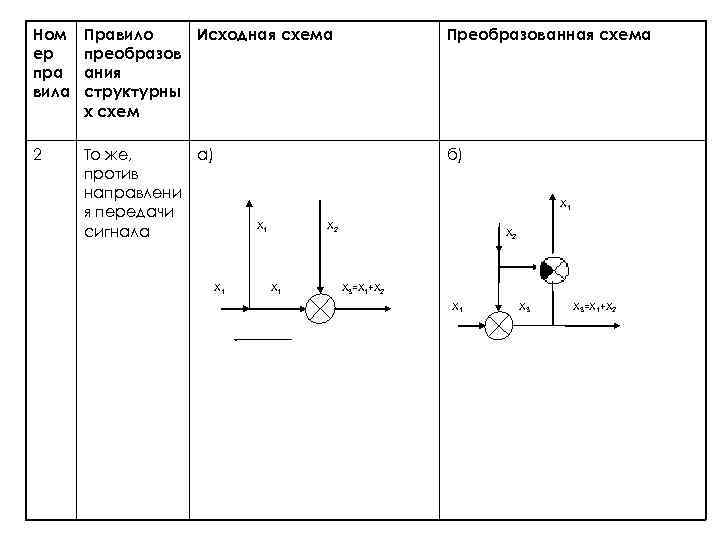Ном ер пра вила Правило Исходная схема преобразов ания структурны х схем Преобразованная схема 2 То же, а) против направлени я передачи сигнала б) X 1 X 1 X 2 X 3=X 1+X 2 X 1 X 3=X 1+X 2

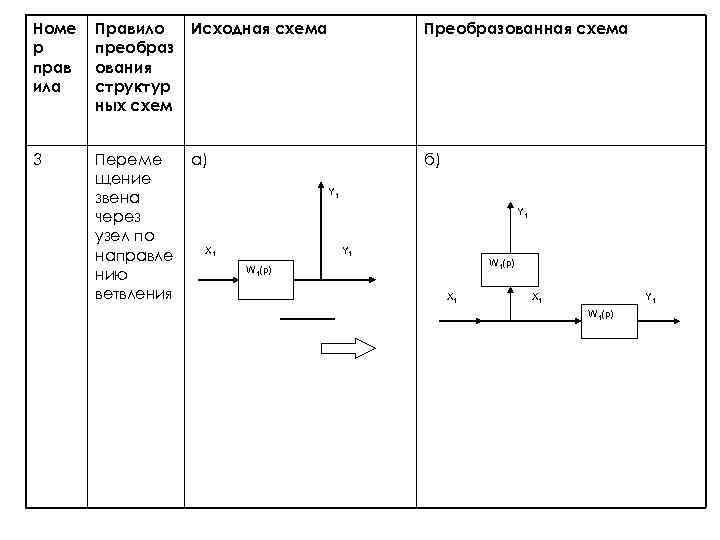Номе р прав ила Правило преобраз ования структур ных схем Исходная схема Преобразованная схема 3 Переме щение звена через узел по направле нию ветвления а) б) Y 1 Y 1 X 1 W 1(p) X 1 Y 1 W 1(p)

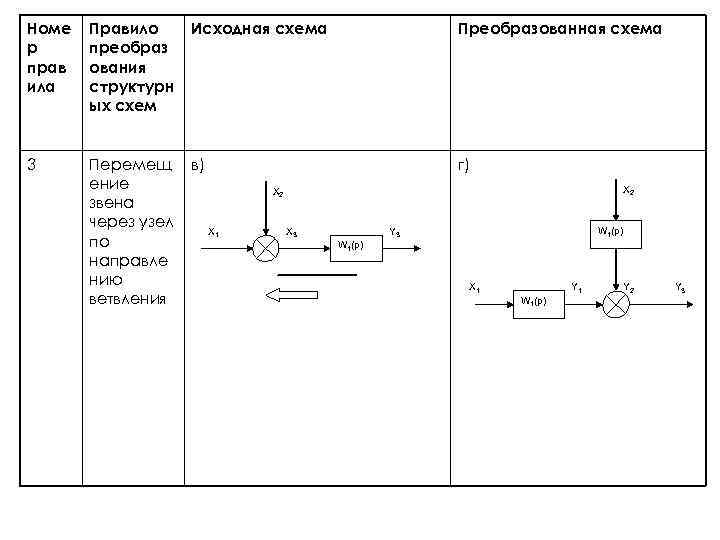Номе р прав ила Правило преобраз ования структурн ых схем Исходная схема Преобразованная схема 3 Перемещ ение звена через узел по направле нию ветвления в) г) X 2 X 1 X 3 W 1(p) Y 3 W 1(p) X 1 Y 1 W 1(p) Y 2 Y 3

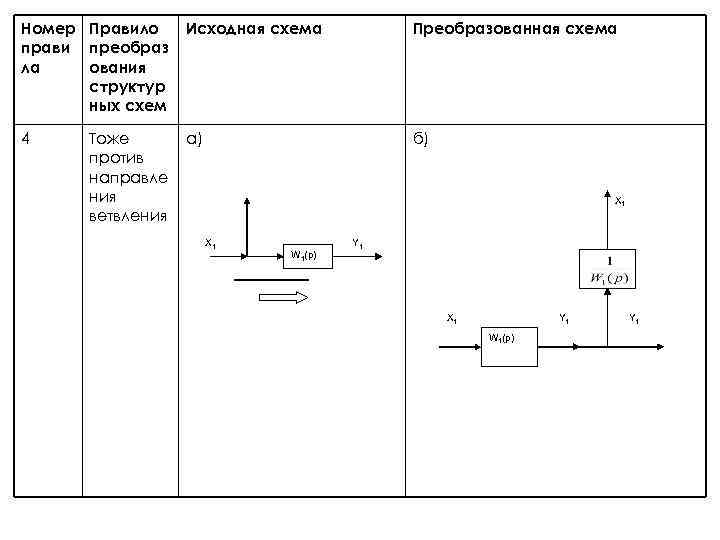Номер Правило прави преобраз ла ования структур ных схем Исходная схема Преобразованная схема 4 а) б) Тоже против направле ния ветвления X 1 W 1(p) Y 1 X 1 Y 1 W 1(p) Y 1

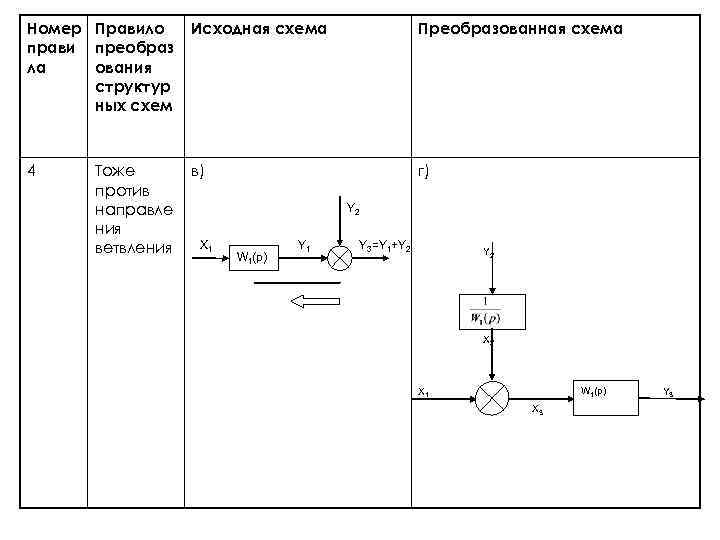Номер Правило прави преобраз ла ования структур ных схем Исходная схема Преобразованная схема 4 в) г) Тоже против направле ния ветвления Y 2 X 1 W 1(p) Y 1 Y 3=Y 1+Y 2 X 2 W 1(p) X 1 X 3 Y 3

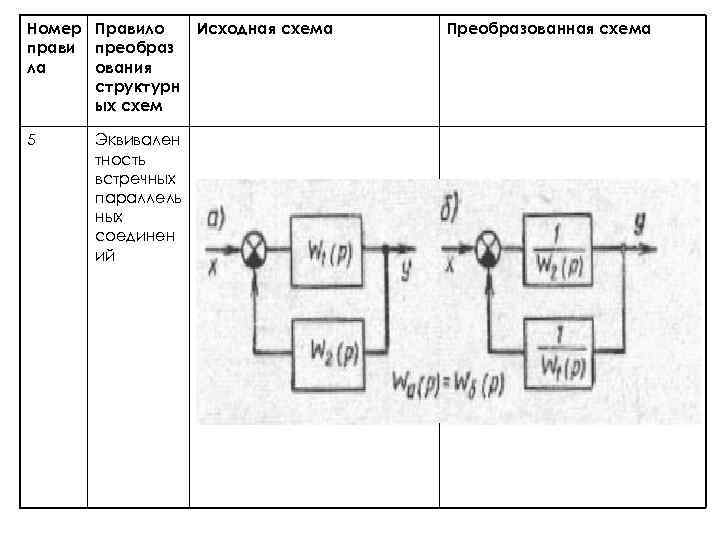Номер Правило прави преобраз ла ования структурн ых схем 5 Эквивален тность встречных параллель ных соединен ий Исходная схема Преобразованная схема

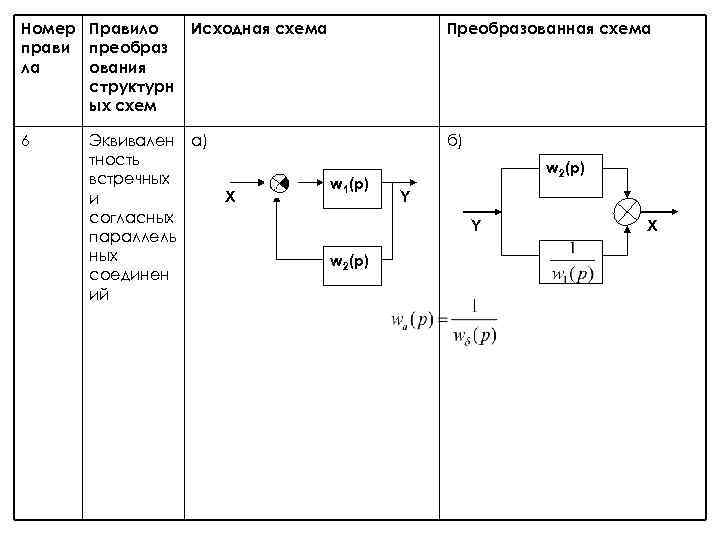Номер Правило прави преобраз ла ования структурн ых схем 6 Исходная схема Эквивален а) тность встречных и согласных параллель ных соединен ий Преобразованная схема б) X w 1(p) w 2(p) Y Y w 2(p) X

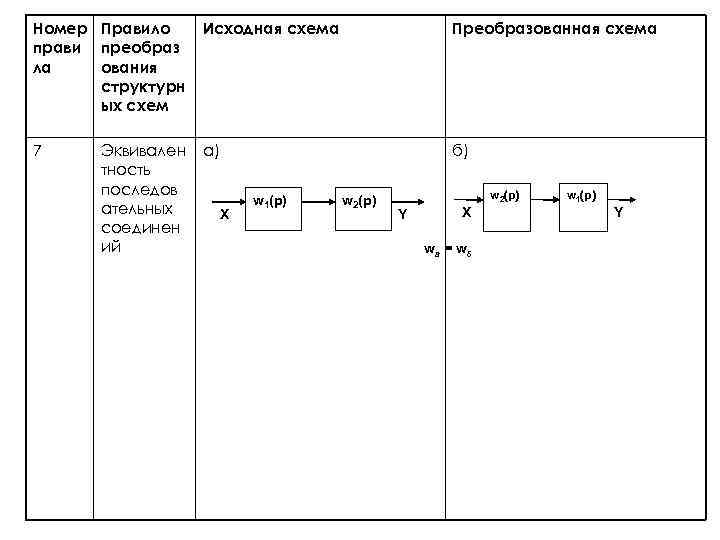Номер Правило прави преобраз ла ования структурн ых схем Исходная схема Преобразованная схема 7 а) б) Эквивален тность последов ательных соединен ий X w 1(p) w 2(p) Y X wа = wδ w 1(p) Y

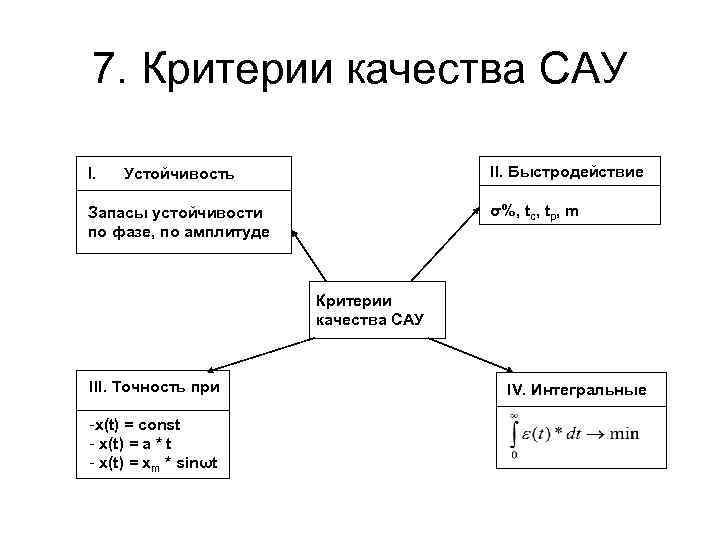7. Критерии качества САУ I. II. Быстродействие Устойчивость σ%, tс, tp, m Запасы устойчивости по фазе, по амплитуде Критерии качества САУ III. Точность при -х(t) = const - x(t) = a * t - x(t) = xm * sinωt IV. Интегральные