Основы теории надежности РЭС Цели и задачи

Основы теории надежности РЭС

Цели и задачи дисциплины Цель данной дисциплины заключается в приобретении студентами знаний в области современной теории надежности и формировании навыков постановки и решения типовых задач оценки обеспечения и оптимизации надежности электронных средств и технических процессов Основные задачи: Изучение гос. стандартов класса «Надежность в технике» Изучение теоретических основ и математического анализа, используемого для расчета, прогнозирования и оптимизации показателей надежности электронных средств и технических процессов Изучение методов анализа и синтеза ЭС по показателям надежности Методы обеспечения и повышения надежности электронных средств и технических процессов

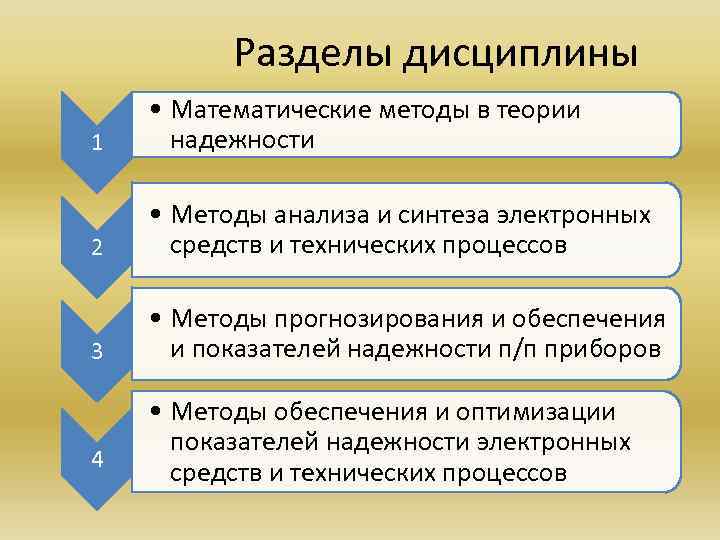Разделы дисциплины 1 • Математические методы в теории надежности 2 • Методы анализа и синтеза электронных средств и технических процессов 3 • Методы прогнозирования и обеспечения и показателей надежности п/п приборов 4 • Методы обеспечения и оптимизации показателей надежности электронных средств и технических процессов

Учебно методическое обеспечение дисциплины Литература • ГОСТ 27. 301 -95 Надежность в технике. Расчет надежности. • Половко А. М. , Гурлов С. В. Основы теории надежности. -2 изд. пер. и доп. -СПб. : БХВПитерберг, 2006. -704 с. • Кофанов Ю. Н. Теоретические основы конструирования, технологии и надежности РЭС. уч. для вузов. -М. : . Радио и связь, : 1991. -360 с. • Андреев А. И. Надежность РЭС. СПб. : 2001 -193 с. • Козлов Б. А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. -М. : Сов. радио, 1967. -4 • Гнеденко Б. В. , Беляев Ю. И. математические методы в теории надежности. —М. : наука, 1965. 524 с. • надежность и эффективность в технике. Справочник в 10 томах. М. : Машиностроение • Левин Б. Р. Теория надежности радиотехнических систем (мат. основы). : Уч. пос. М. : радио и связь, 1983 312 с. • Дилон Б. , Сингх Ч. Инженерные методы обеспечения надежности систем. Пер. с англ. М: Мир, 1984 314 с. • Труханов В. М. Надежность технических систем типа подвижных установок на этапе проектирования и испытаний опытных образцов. М. : машиностроение, 2003 320 с. • Дубицкий Л. Г. Предвестники отказов в изделиях электронной техники. М. : радио и связь, 1989. 96 с. • Каниовская И. М. Курс лекций по дисциплине «Инженерные методы расчета надежности»

Развитие радиоэлектроники оказывает существенное влияние на научно-технический прогресс и успехи в социально-экономической области. Машиностроение, которое играет ключевую роль в ускорении научнотехнического прогресса, нуждается в надежно работающих сложных изделиях радиоэлектроники, органически входящих в качестве комплектующих элементов в станки с числовым программным управлением, роботы и другие устройства гибких производственных систем. Транспорт, энергетика, космические системы и другие направления нашей экономики, где велики последствия одногоединственного отказа, также нуждаются в высоконадежных изделиях радиоэлектроники. Надежность этих изделий закладывается при их проектировании, обеспечивается при производстве и поддерживается при эксплуатации в составе РЭС. С другой стороны, изделия радиоэлектроники должны рассматриваться как результат разработки схемы, конструкции и технологии.

Основные свойства технических систем Объект – техническое изделие определенного целевого назначения, рассматриваемое в периоды проектирования, производства, испытаний и эксплуатации. Объектами могут быть различные системы и их элементы, в частности: сооружения, установки, технические изделия, устройства, машины, аппараты, приборы и их части, агрегаты и отдельные детали. Элемент системы – объект, представляющий отдельную часть системы. Само понятие элемента условно и относительно, так как любой элемент, в свою очередь, всегда можно рассматривать как совокупность других элементов. Понятия система и элемент выражены друг через друга, поскольку одно из них следовало бы принять в качестве исходного, постулировать. Понятия эти относительны: объект, считавшийся системой в одном исследовании, может рассматриваться как элемент, если изучается объект большего масштаба. Кроме того, само деление системы на элементы зависит от характера рассмотрения (функциональные, конструктивные, схемные или оперативные элементы), требуемой точности проводимого исследования, уровня наших представлений, от объекта в целом. Человек-оператор также представляет собой одно из звеньев системы человек – машина. Система – объект, представляющий собой совокупность элементов, связанных между собой определенными отношениями взаимодействующих таким образом, чтобы обеспечить выполнение системой некоторой доста точно сложной функции. Признаком системности является структурированность системы, взаимосвязанность составляющих ее частей, подчиненность организации всей системы определенной цели. Системы функционируют в пространстве и времени

Технику обычно классифицируют по отраслевой структуре производства (например, промышленности, транспорта) или применительно к отдельным структурным подразделениям производства. Например, техника авиационная, мелиоративная, энергетическая, химическая, горная и т. п. Под технической системой (объектом) понимается упорядоченная совокупность отдельных элементов, связанных между собой функционально и взаимодействующих таким образом, чтобы обеспечить выполнение некоторых заданных функций (достижение цели) при различных состояниях работоспособности. Объектами могут быть различные системы и их элементы, в частности: сооружения, установки, технические изделия, устройства, машины, аппараты, приборы и их части, агрегаты и отдельные детали. Признаком системы является структурированность, взаимосвязанность составляющих ее частей, подчиненность организации всей системы определенной цели. Обязательным компонентом любой системы являются составляющие элементы (подсистемы), само понятие элемента условно и относительно, так как любой элемент, в свою очередь, всегда можно рассматривать как совокупность других элементов. Поскольку все подсистемы и элементы, из которых состоит система, определенным образом взаиморасположены и взаимосвязаны, образуя данную систему, можно говорить о структуре системы. Структура системы – это то, что остается неизменным в системе при изменении ее состояния.

Понятия радиоэлектроники и радиотехники. Радиоэлектроника – это область науки и техники, охватывающая широкой круг вопросов использования электромагнитной энергии для передачи, приема и преобразования сигналов и содержащейся в них информации. Радиотехника – область науки и техники, связанная с генерированием, преобразованием, излучением и приемом электромагнитных колебаний и волн радиочастотного диапазона. В соответствии с международным регламентом границы радиочастот лежат в пределах 3 к. Гц … 3 ГГц, которым соответствуют длины волн от 100 км до 0, 1 мм. Радиоэлектронное средство - техническое изделие определенной сложности или его составная часть, в основу действия которого положены принципы радиотехники и электроники. Радиоэлектронная система (РЭ система) – это РЭС в виде совокупности функционально взаимодействующих автономных радиоэлектронных комплексов и устройств, которые образуют целостное единство, обладающее свойством перестроения структуры в целях рационального выбора и использования входящих средств нижних уровней при решении технических задач.

Понятия радиоэлектроники и радиотехники (продолжение) Радиотехническая система - разновидность РЭ системы, под которой понимают совокупность РЭС для передачи сообщений и команд по радиоканалам, состоящих из радиопередатчиков, линий радиосвязи и радиоприемников. Вычислительная система - разновидность РЭ системы, определяемая как взаимосвязанная совокупность вычислительных комплексов и устройств, согласованных по быстродействию, пропускной способности и другим параметрам. Радиоэлектронный комплекс (РЭК) – это РЭС в виде совокупности функционально связанных РЭУ, обладающих свойством изменения структуры в целях сохранения работоспособности при выполнении технических задач в составе РЭ системы или в режиме самостоятельного применения. Радиоэлектронной устройство (РЭУ) – есть РЭС в виде функционально законченной сборочной единицы, которая выполнена на несущей конструкции и реализует функции приема, преобразования и передачи информации или решает техническую задачу на их основе

Понятия радиоэлектроники и радиотехники (продолжение) Электрическая схема РЭС – совокупность РЭ, соединенных между собой в соответствии с заданным принципом действия РЭ системы или в соответствии с функциями, выполняемыми данным РЭС внутри другого РЭС более высокого уровня Схемотехника – прикладная научная дисциплина, занимающаяся анализом и синтезом электрических схем РЭС Конструкция РЭС – совокупность изделий электронной техники (ИЭТ), электротехнических изделий (ЭТИ) и конструктивных деталей, находящихся в определенной пространственно-механической, информационной и энергетической взаимосвязи, которая обеспечивает выполнение данным РЭС необходимых функций с высокой надежностью. Надежность – это свойство РЭС сохранять во времени в установленных пределах значения всех требуемых характеристик, параметров и показателей при заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.

Понятия радиоэлектроники и радиотехники (продолжение) Технология РЭС как область техники – совокупность способов обработки, изменения состояния, свойств и формы материалов, изготовления полуфабрикатов (деталей, узлов, устройств) и их сборки с определенной точностью и производительностью в процессе производства для получения готового РЭС. С другой стороны, технология РЭС как прикладная научная дисциплина – это обобщенное представление физических химических, механических и других закономерностей и методов воздействия на материалы соответствующими орудиями производства. Эксплуатация РЭС как область техники – совокупность способов транспортировки, хранения, установки и технического обслуживания РЭС при их функциональном использовании по назначению. В то же время эксплуатация РЭС как прикладная научная дисциплина – это системное представление и условий наилучшего использования аппаратуры для заданных целей с высокой надежностью и эффективностью.

Основные понятия надежности технических систем Термины надежность, безопасность, опасность и риск часто смешивают, при этом их значения перекрываются. Часто термины анализ безопасности или анализ опасности используются как равнозначные понятия. Наряду с термином анализ надежности они относятся к исследованию как работоспособности, отказов оборудования, потери работоспособности, так и процесса их возникновения. Обеспечение надежности систем охватывает самые различные аспекты человеческой деятельности. Надежность является одной из важнейших характеристик, учитываемых на этапах разработки, проектирования и эксплуатации самых различных технических систем. Надежность. В соответствии с ГОСТ 27. 002 89 под надежностью понимают свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.

Основные положения теории надёжности. Теория надёжности, как научное направление, сформировалась в последние 20 30 лет в результате разностороннего теоретического и экспериментального изучения закономерностей, связанных с обеспечением безотказной работы современных технических средств Теория надёжности рассматривает: • закономерности возникновения отказов и восстановления работоспособности машин, механизмов, аппаратов, приборов, устройств; • влияние внешних и внутренних воздействий на процессы в технических устройствах; • методы количественного определения и сравнительной оценки надёжности; • мероприятия по повышению надёжности при конструировании и производстве машин, а также способы поддержания необходимого уровня их надёжности в процессе эксплуатации.

Надежность объекта является комплексным свойством, ее оценивают по четырем показателям — безотказности, долговечности, ремонтопригодности и сохраняемости или по сочетанию этих свойств. Безотказность — свойство объекта сохранять работоспособность непрерывно в течение некоторого времени или некоторой наработки. Это свойство особенно важно для машин, отказ в работе которых связан с опасностью для жизни людей. Безотказность свойственна объекту в любом из возможных режимов его существования, в том числе, при хранении и транспортировке. Долговечность — свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Предельное состояние — состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно. Ремонтопригодность — свойство объекта, заключающееся в его приспособленности к поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонта. Важность ремонтопригодности технических систем определяется огромными затратами на ремонт машин. Сохраняемость — свойство объекта сохранять в заданных пределах значения параметров, характеризующих способность объекта выполнять требуемые функции, в течение и после хранения и (или) транспортирования.

Надежность объекта характеризуется следующими состояниями: исправное, неисправное, работоспособное, неработоспособное. Исправное состояние — такое состояние объекта, при котором он соответствует всем требованиям нормативно технической и (или) конструкторской (проектной) документации. Исправное изделие обязательно работоспособно. Неисправное состояние — такое состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно технической и (или) конструкторской (проектной) документации. Различают неисправности, не приводящие к отказам, и неисправности, приводящие к отказам. Например, повреждение окраски автомобиля означает его неисправное состояние, но такой автомобиль работоспособен. Работоспособным состоянием называют такое состояние объекта, при котором он способен выполнять заданные функции, соответствующие требованиям нормативно технической и (или) конструкторской (проектной) документации. Неработоспособное изделие является одновременно неисправным.

Важной задачей науки о надёжности является изучение физических причин отказов, а также разработка теоретических основ и методов ускоренных испытаний на надёжность, обеспечивающих возможность оценки эксплуатационной надёжности машин

Отказ — событие, заключающееся в нарушении работоспособного состояния объекта. Отказы по характеру возникновения подразделяют на случайные и неслучайные (систематические). Случайные отказы вызваны непредусмотренными нагрузками, скрытыми дефектами материалов, погрешностями изготовления, ошибками обслуживающего персонала. Неслучайные отказы — это закономерные явления, вызывающие постепенное накопление повреждений, связанные с влиянием среды, времени, температуры, облучения и т. п. В зависимости от возможности прогнозировать момент наступления отказа все отказы подразделяют на внезапные (поломки, заедания, отключения) и постепенные (износ, старение, коррозия). По причинам возникновения отказы классифицируют на конструктивные (вызванные недостатками конструкции), производственные (вызванные нарушениями технологии изготовления) и эксплуатационные (вызванные неправильной эксплуатацией).

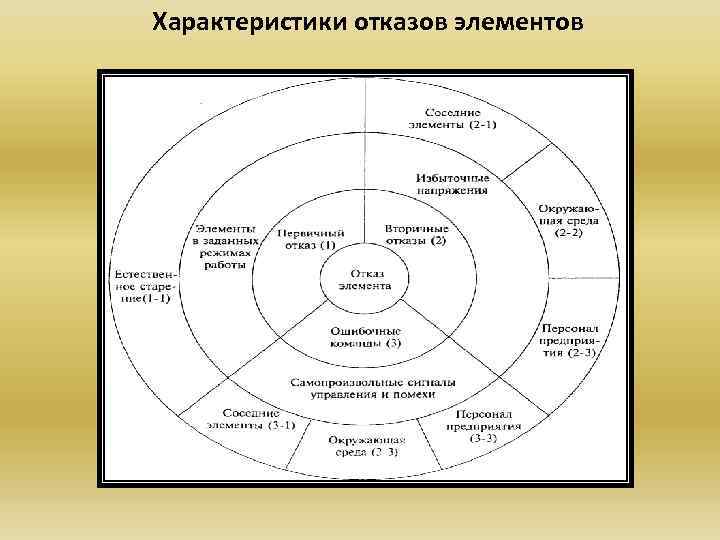Характеристики отказов элементов

Показатели надежности Показателями надежности называют количественные характеристики одного или нескольких свойств объекта, составляющих его надежность. К таким характеристикам относят, например, временные понятия — наработку, наработку до отказа, наработку между отказами, ресурс, срок службы, время восстановления. Значения этих показателей получают по результатам испытаний или эксплуатации. По восстанавливаемости изделий показатели надежности подразделяют на показатели для восстанавливаемых изделий и показатели невосстанавливаемых изделий. Применяются также комплексные показатели. Надежность изделий, в зависимости от их назначения, можно оценивать, используя либо часть показателей надежности, либо все показатели.

Показатели безотказности: Ø вероятность безотказной работы — вероятность того, что в пределах заданной наработки отказ объекта не возникает; Ø средняя наработка до отказа — математическое ожидание наработки объекта до первого отказа; Ø средняя наработка на отказ — отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки; Ø интенсивность отказов — условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Этот показатель относится к невосстанавливаемым изделиям.

Показатели долговечности. Показатели, связанные со сроком службы изделия: Øсрок службы — календарная продолжительность эксплуатации от начала эксплуатации объекта или ее возобновление после ремонта до перехода в предельное состояние; Ø средний срок службы — математическое ожидание срока службы; Øсрок службы до первого капитального ремонта агрегата или узла – это продолжительность эксплуатации до ремонта, выполняемого для восстановления исправности и полного или близкого к полному восстановления ресурса изделия с заменой или восстановлением любых его частей, включая базовые; Ø срок службы между капитальными ремонтами, зависящий преимущественно от качества ремонта, т. е. от того, в какой степени восстановлен их ресурс; Øсуммарный срок службы – это календарная продолжительность работы технической системы от начала эксплуатации до выбраковки с учетом времени работы после ремонта; Ø гамма-процентный срок службы — календарная продолжительность эксплуатации, в течение которой объект не достигнет предельного состояния с вероятностью γ, выраженной в процентах.

Показатели долговечности. Показатели, связанные с ресурсом изделия: Øресурс — суммарная наработка объекта от начала его эксплуатации или ее возобновление после ремонта до перехода в предельное состояние. Øсредний ресурс — математическое ожидание ресурса; для технических систем в качестве критерия долговечности используют технический ресурс; Øназначенный ресурс – суммарная наработка, при достижении которой эксплуатация объекта должна быть прекращена независимо от его технического состояния; Øгамма-процентный ресурс — суммарная наработка, в течение которой объект не дотигнет предельного состояния с заданной вероятностью γ, выраженной в процентах.

Критерии и количественные характеристики надежности Критерием надежности называется признак, по которому можно количественно оценить надежность различных устройств. К числу наиболее широко применяемых критериев надежности относятся: 1– вероятность безотказной работы в течение определенного времени Р(t); 2– средняя наработка до первого отказа Тср; 3– наработка на отказ tcp; 4– частота отказов f(t) или a(t); 5– интенсивность отказов λ(t);

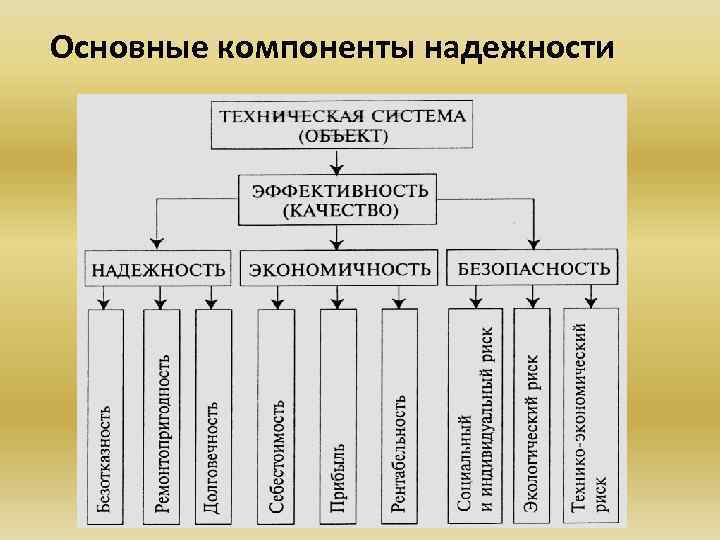Основные компоненты надежности

Любые системы можно подразделить на простые и сложные. Системы, в которых условная эффективность (относительно событий отказа элементов) может принимать только 2 дискретных значения является простой. Все остальные системы – сложными. При рассмотрении теории надежности и эффективности удобно представлять физическую модель системы в виде многополюсника с входным и выходными параметрами. Входные: параметры входных сигналов, элементов системы, параметры внешней и внутренней сред и т. д. . Выходные: амплитудно частотные, фазочастотные характеристики, импеданс, чувствительность и избирательность приемника, показатели точности, надежности и эффективности системы. Среди входных параметров можно условно выделить первичные параметры, к которым относятся параметры элементов и устройств системы, которые непосредственно воспринимают воздействие внешней и внутренней среды и , изменяя которые можно управлять качеством системы на этапах разработки, изготовления и эксплуатации. Выходные параметры системы некоторым оператором связаны с входными параметрами. При изменении входных – выходные параметры также изменятся.

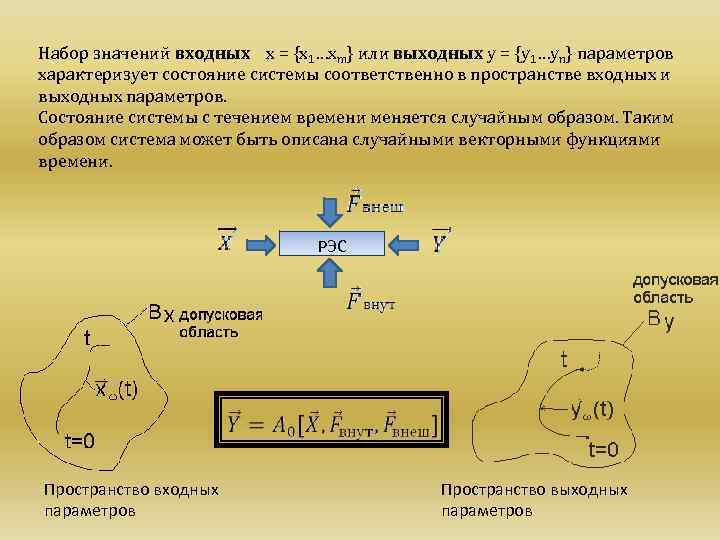Набор значений входных х = {x 1…xm} или выходных y = {y 1…yn} параметров характеризует состояние системы соответственно в пространстве входных и выходных параметров. Состояние системы с течением времени меняется случайным образом. Таким образом система может быть описана случайными векторными функциями времени. РЭС Пространство входных параметров Пространство выходных параметров

Случайность выходного параметра Y определяется случайным характером воздействия Рвнут. , Рвнеш. и случайностью самих параметров х (например, разбросом значений), при детермини рованном операторе системы. Могут быть системы со случайным оператором, который изменяется в зависимости от некоторых состояний системы и среды (так называемые адаптивные системы, т. е. приспосабливающиеся системы). Эволюция состояний в общем случае описывается случайными функциям x(t), Y(t). Так как оператор связи параметров сред Рвнут. , Рвнеш. с входными параметрами часто неизвестен, то из за этого случайный характер первичных параметров усиливается, и требуются специальные испытания и исследования для определения статистических характеристик х в условиях воздействия внешней и внутренней сред. В этом случае выражение запишем в другом виде: Y = A{x}

В пространстве входных или выходных параметров у ряда систем можно выделить соответствующие области Вх или By, в пределах которых условная эффективность не зависит от эволюции технического состояния и остается постоянной, а за пределами этой области она равна нулю. Подобные системы называют простыми. Для них справедлива запись Область Вх является отображением области By. Эти области характеризуют области определения функции и ее аргументов и их можно назвать допусковыми областями на входные или выходные параметры.

Системы, в которых не удается четко выделить аналогичные области, называются сложными системами. Иногда сложные системы в первом приближении сводят к простым, задав предельный уровень снижения условной эффективности. В этом случае можно определить границу допусковых областей, но уже для эквивалентной в некотором смысле простой системы и дать определение ее отказа. При современном уровне интеграции можно создать системы с большим числом элементов и большой структурной избыточностью, но все же они будут относиться к простым системам. Большие системы, как правило, одновременно бывает и сложным (в указанном смысле), так как при конструировании для повышения их живучести обеспечивается не бинарное значение условной эффективности при возникновении тех или иных неисправностей в подсистемах и элементах.

Основные показатели надежности простых систем В простых системах время пребывания изображающей состояние точки в допусковой области называется временем "жизни". Выход изображающей состояние точки за границы Вх или By является отказом простой системы. После отказа восстанавливаемые системы ремонтируются, и от качества ремонта зависит будущее время "жизни" системы. Во всех случаях время "жизни" представляет собой случайную величину и характеризуется функцией распределения, плотностью вероятности или моментами случайной величины. Время "жизни" до 1 го отказа Тж Время "жизни" между отказами (для восстанавливаемых систем) Тж

Исчерпывавшей характеристикой времени "жизни" является функция распределения. F 1(t) = τ{Tж (1) < t } или F(t) = τ { Tж < t } Функция распределения F 1(t) определяет вероятность возникновения первого отказа на интервале (О, t), a F(t) вероятность отказа на интервале (t(к) , t (к)+ t). t – момент к го восстановления системы Отсчет времени t производится от момента предыдущего отказа (восстановления). Вероятность отказа на интервале (0, t) или (t(к) , t(к) + t) обозначается через Q 1(t) или Q(t). Q 1(t)=F 1(t) или Q(t)=F(t) Как правило, Qi(t) = Q(t) = Fi(t) = F(t).

Как правило, справедливо равенство P 1(t) = P(t). Если функция F 1(t) или F(t) дифференцируема, то существует плотность вероятности времени "жизни" f 1 (t)= (d/dt) F 1(t) = (d/dt)Q 1(t) = (d/dt) P 1 (t) или f(t)= (d/dt) F(t) = (d/dt)Q(t) = (d/dt)P(t) Как правило, fi(t) = f(t). F(t)= ʃ f(τ)dτ и P(t) = ʃ f(τ) dτ. Если отсчитывать время работы объекта от произвольного не случайного времени t, то для достаточно удаленного t →∞ на практике существует стационарная вероятность безотказной работы системы Р∞(τ) на интервале (t, t + τ), не зависящая от t. Так как после каждого отказа система восстанавливается, и момент t может совпасть со случайным периодом восстановления, то для определения стационарной вероятности безотказной работы необходимо учесть характеристики случайного времени восстановления ξ

Исчерпывающей характеристикой времени является функция распределения времени восстановления FB(t) (предполагается, что эта функция не зависит от номера отказа). FB(t) = P{ξ ≤ t} По аналогии с плотностью вероятности времени "жизни" рассматривается, и плотность вероятности времени восстановления f. B(t) = (d/dt)FB(t) Также исчерпывающими характеристиками времени "жизни" до 1 го отказа и времени восстановления являются специально введенные функции вида λ (t) = f 1(t) / (1 – F 1(t)) μ(t) = f(t) / (1 - F(t))

В общем же случае для характеристики восстанавливаемых систем, когда последовательные отказы образуют случайней поток отказов и соответственно поток восстановлений, используют поня тие параметра потока. При отсутствии групповых отказов в один и тот же момент времени (ординарный поток) параметр потока ω определяется. ω= lim (РΔ=1 (t, t + τ)) / τ = Р 1 (t) где РΔ =1 (t, t + τ) вероятность появления ровно одного отказа (Δ = 1) на интервале (t, t + τ). Важной характеристикой восстанавливаемых систем является: функция восстановления (H(t)), которая равна среднему числу отказов (восстановлений), происшедших на интервале (0, t), a также плотность восстановления h(t), равная производной от функции восстановления: h(t) = (d/dt) H(t)

Функция восстановления и плотность восстановления связаны с функцией распределения и плотностью вероятности времени "жизни" интегральными уравнениями H(t)= F(t) =ʃ H(t τ) d. F(τ) H(t)= f(t) +ʃ h(t τ) f(τ)dτ Интерес представляет стационарный случай при t →∞. При t →∞ lim h(t) = 1/Т, lim (H(t)/t) = (1/ Т), H(t) ≈ (t/T) + (σt 2/2 T 2) 1/2, для больших t, где σt 2 дисперсия времени "жизни", Т = М [Тж] = ʃ P(τ)dτ Зная H(t) можно найти среднее число n(t, t 2) отказов на интервале (t 1, t 2) N (t 1, t 2) = H(t 2) H(t 1)

Для характеристики восстанавливаемых систем часто используется коэффициент готовности Kr(t), который равен вероятности того, что в момент t система будет готова к применению. Обычно рассматривается стационарное значение коэффициента готовности Кг, не зависящее от t (при t →ω). Кr = Т / (Т+Тв) Cтационарная вероятность безотказной работы на интервале (t, t +x ) при t →ω равна P∞(τ)=l/(T+TB) ʃ(l F(t))dt Легко заметить, что при τ = 0 Р(0) = Кr. Важно еще раз подчеркнуть, что P∞(τ) характеризует вероятность безотказной работы за время τ, отсчитываемого от неслучайного достаточно удаленного момента t. Если же τ отсчитывать от случайного момента последнего полного восстановления, то P(t) = 1 τ(t)

Сводка показателей надежности простых РЭС: üP(t) вероятность безотказной работы на интервале ( 0, t) или (τi, τi + τ), где τi случайный момент i го полного восстановления системы (τ начало отсчета); üQ(t) вероятность отказа на интервале ( 0, t) или (τi, τi + τ); üPt(x) вероятность безотказной работы на интервале (t, t + τ), где t не случайный момент отсчета; üP∞(τ) стационарная вероятность безотказной работы; üQt(τ) вероятность отказа на интервале (t, t + τ); üQ∞(τ) стационарная вероятность отказа на интервале (t, t + τ ) при t →∞ üТ 0 средняя наработка до отказа (для РЭС без восстановления); üf(t) плотность вероятности отказа; üλ(t), μ. (t) соответственно интенсивность отказа и восстановления; üТ среднее время "жизни" (для РЭС с восстановлением) до первого üотказа или между отказами (средняя наработка на отказ); üТв среднее время восстановления; üω(t) параметр потока отказов или восстановлений; üH(t) функция восстановления; . üh(t) плотность восстановления

Если к моменту t. K (момент контроля) стало известно, что система исправна, (Тж > tk), то апостериорная (условная) функция распределения имеет вид f РΔ ((t /Тж) > t. K ) = f(t) /( ʃ f(x) dx ) = f(t) / ( 1 - F(t. K)) Апостериорная вероятность безотказной работы равна: Р PA((t /Тж) > t. K ) = 1 – τ ((t /Тж) > t. K ) = P(t)/P(t. K) где P(t) = ʃ f(τ) dτ, P(t. K) = ʃ f(τ)dτ при t ≥ t. K Можем рассматривать апостериорную (условную) интенсивность отказа λ PΔ((t /Тж) > t. K) = f PΔ((t /Тж) > t. K) / [ 1 - F PΔ((t /Тж) > t. K )] Может наблюдаться более сложное событие "В" по сравнению с Тж > t. K. Тогда используются условные законы f(t / В), F(t/B). Апостериорное среднее время "жизни" (оставшееся среднее время "жизни") определяется формулой Т РΔ(Тж > t. K) = ʃ Р РΔ(Тж > t. K) dt где Т РΔ отсчитывается от t. K

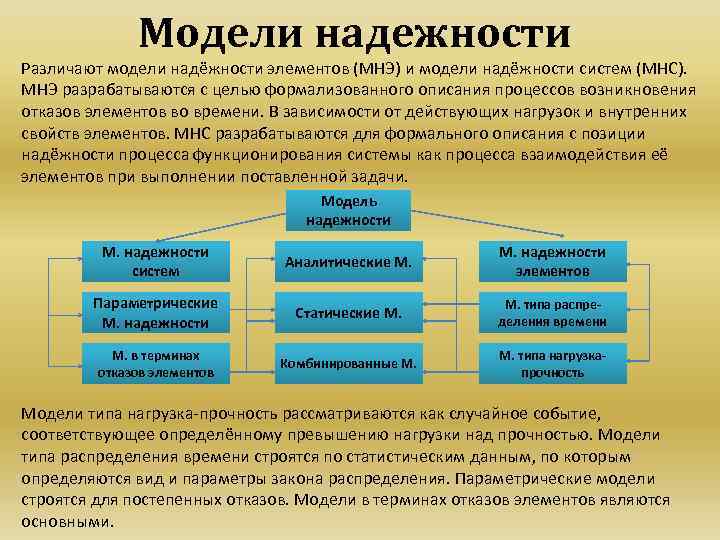Модели надежности Различают модели надёжности элементов (МНЭ) и модели надёжности систем (МНС). МНЭ разрабатываются с целью формализованного описания процессов возникновения отказов элементов во времени. В зависимости от действующих нагрузок и внутренних свойств элементов. МНС разрабатываются для формального описания с позиции надёжности процесса функционирования системы как процесса взаимодействия её элементов при выполнении поставленной задачи. Модель надежности М. надежности систем Аналитические М. надежности элементов Параметрические М. надежности Статические М. типа распределения времени М. в терминах отказов элементов Комбинированные М. типа нагрузкапрочность Модели типа нагрузка прочность рассматриваются как случайное событие, соответствующее определённому превышению нагрузки над прочностью. Модели типа распределения времени строятся по статистическим данным, по которым определяются вид и параметры закона распределения. Параметрические модели строятся для постепенных отказов. Модели в терминах отказов элементов являются основными.

Методы повышения надежности технических систем «Жизненный» цикл технической системы содержит следующие основные этапы: проектирование, производство, эксплуатация (применение по назначению). На каждом из этих этапов существуют и успешно применяются различные методы повышения и поддержания надежности. Наиболее эффективно методы повышения надежности используются на этапе проектирования, когда «закладываются» соответствующие показатели надежности. На последующих этапах задача, прежде всего, сводится к обеспечению и (или) поддержанию заложенных показателей надежности. Это не означает, что на этапах производства и эксплуатации такие показатели не могут быть улучшены, однако подобный результат будет достигаться более дорогой ценой (более высокая стоимость, большее время и т. п. ). Методы повышения надежности, используемые в настоящее время, могут быть разделены на группы: 1. Методы, связанные с увеличением надежности комплектующих изделий за счет применения новых принципов, конструкций, материалов, технологии изготовления и т. п. 2. Методы, защищающие элементы технических систем от воздействия внешней среды. 3. Методы рационального проектирования, приводящие к уменьшению общего числа элементов, снижению переходных процессов и т. п. 4. Методы введения избыточности различного вида. 5. Методы обеспечения надежности за счет стабилизации технологических процессов. 6. Методы предупреждения отказов путем профилактических замен элементов, проявивших признаки износа или старения.

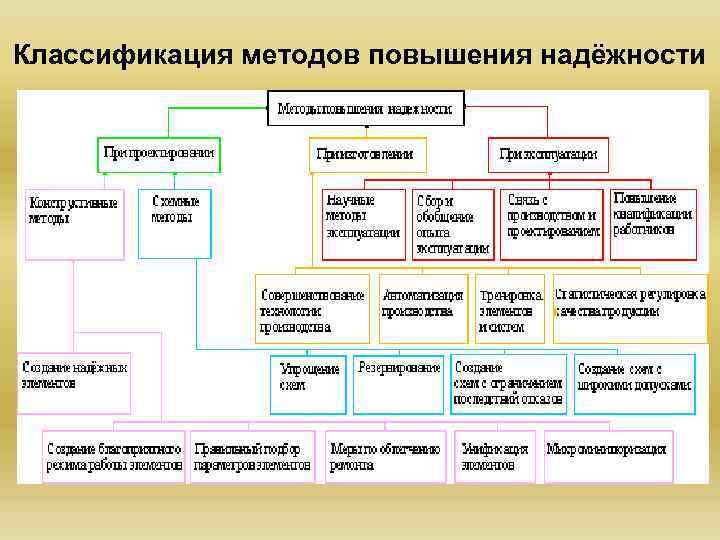Классификация методов повышения надёжности

Резервирование — метод повышения надежности объекта путем введения дополнительных элементов и функциональных возможностей сверх мини мально необходимых для нормального выполнения объектом заданных функций. В этом случае отказ наступает только после отказа основного и всех резервных элементов. Систему можно представить из ряда ступеней, выполняющих отдельные функции. Задача резервирования состоит в нахождении такого числа резервных образцов оборудования на каждой ступени, которое будет обеспечивать заданный уровень надежности системы при наименьшей стоимости. Выбор наилучшего варианта зависит главным образом от того увеличения надежности, которое можно достичь при заданных расходах. Основной элемент — элемент основной физической структуры объекта, минимально необходимой для нормального выполнения объектом его задач. Резервный элемент — элемент, предназначенный для обеспечения работоспособности объекта в случае отказа основного элемента. Виды резервирования Структурное (элементное) резервирование — метод повышения надеж ности объекта, предусматривающий использование избыточных элементов, входящих в физическую структуру объекта. Обеспечивается подключением к основной аппаратуре резервной таким образом, чтобы при отказе основной аппаратуры резервная продолжала выполнять ее функции. Резервирование функциональное — метод повышения надежности объекта, предусматривающий использование способности элементов выполнять дополнительные функции вместо основных и наряду с ними. Временное резервирование — метод повышения надежности объекта, предусматривающий использование избыточного времени, выделенного для выполнения задач. Другими словами, временное резервирование — такое планирование работы системы, при котором создается резерв рабочего вре мени для выполнения заданных функций. Резервное время может быть использовано для повторения операции, либо для устранения неисправности объекта.

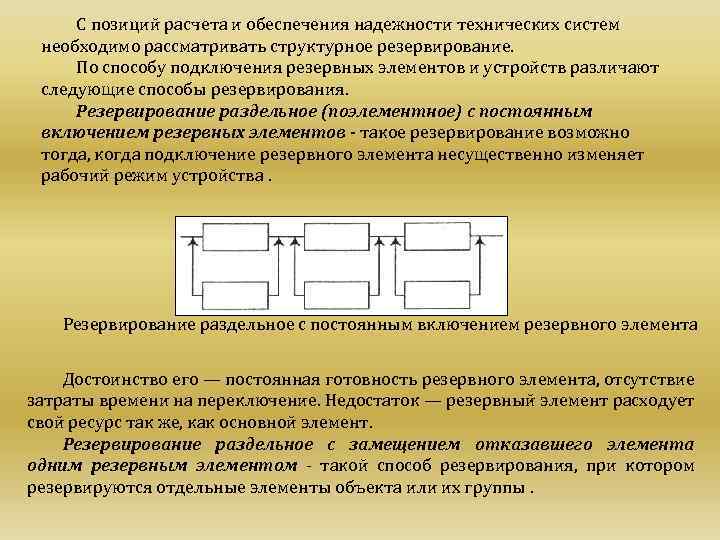С позиций расчета и обеспечения надежности технических систем необходимо рассматривать структурное резервирование. По способу подключения резервных элементов и устройств различают следующие способы резервирования. Резервирование раздельное (поэлементное) с постоянным включением резервных элементов - такое резервирование возможно тогда, когда подключение резервного элемента несущественно изменяет рабочий режим устройства. Резервирование раздельное с постоянным включением резервного элемента Достоинство его — постоянная готовность резервного элемента, отсутствие затраты времени на переключение. Недостаток — резервный элемент расходует свой ресурс так же, как основной элемент. Резервирование раздельное с замещением отказавшего элемента одним резервным элементом такой способ резервирования, при котором резервируются отдельные элементы объекта или их группы.

Резервирование раздельное с замещением отказавшего элемента В этом случае резервный элемент находится в разной степени готовности к замене основного элемента. Достоинство этого способа в том, что резервный элемент сохраняет свой рабочий ресурс, либо может быть использован для выполнения самостоятельной задачи. Рабочий режим основного устройства не искажается. Недостаток способа в том, что необходимость затрачивать время на подключение резервного элемен та. Резервных элементов может быть меньше, чем основных. Отношение числа резервных элементов к числу резервируемых называется кратностью резервирования — т. При резервировании с целой кратностью величина т есть целое число, при резервировании с дробной кратностью величина т есть дробное несокращаемое число. Например, т = 4/2 означает наличие ре зервированияс дробной кратностью, при котором число резервных элемен товравно четырем, число основных — двум, а общее число элементов равно шести. Сокращать дробь нельзя, так как если т = 4/2 = 2/1, то это означает, что имеет место резервирование с целой кратностью, при котором число ре зервныхэлементов равно двум, а общее число элементов равно трем.

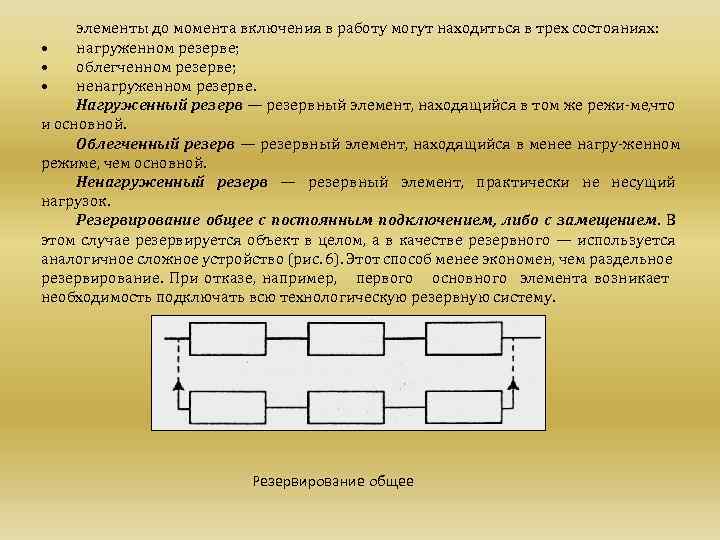элементы до момента включения в работу могут находиться в трех состояниях: • нагруженном резерве; • облегченном резерве; • ненагруженном резерве. Нагруженный резерв — резервный элемент, находящийся в том же режи ме, что и основной. Облегченный резерв — резервный элемент, находящийся в менее нагру женном режиме, чем основной. Ненагруженный резерв — резервный элемент, практически не несущий нагрузок. Резервирование общее с постоянным подключением, либо с замещением. В этом случае резервируется объект в целом, а в качестве резервного — используется аналогичное сложное устройство (рис. 6). Этот способ менее экономен, чем раздельное резервирование. При отказе, например, первого основного элемента возникает необходимость подключать всю технологическую резервную систему. Резервирование общее

Основные законы распределения, используемые в теории надежности При любом законе распределения можно получить выражение для вероятности безотказной работы P(t) на основе знания X(t). λ(t) = - (P 1(t) / P(t)) = - (d/dt) In P(t) Отсюда P(t)=eхр(-ʃ λ(ν)dν) при Р(0)=1

Экспоненциальный закон. При λ(v) = λ = const получим так называемый экспоненциальный закон распределения. Для этого закона справедливы следующие соотношения: f(t) = k exp( λt) T=l/λ; σt=l/λ 2 Р∞(τ) = kr еxp ( λt) ; kr = Т/(Т +Тв) h(t) = ω(t) = λ F(t) = 1 – exp ( λt ) n(t 1, t 2) = λ(t 2 t 1) P(t) = exp( λt) H(t) = ht = λt При λt << 1 удобно пользоваться приближением exp( λt) ≈ 1 λt.

Закон Вейбулла. Для него справедливы следующие соотношения P(t) = еxp (-λ 0 ta) F(t) = 1 - еxp (-λ 0 ta) f(t) = λ 0 ata-1 еxp (-λ 0 ta) Т=1/(λ 1/2) Г((1/а)+1) где Г ((1/а) + 1) гамма функция. λ (t) = λ 0 a t a-1 (при а > 1, λ(t) возрастает, а при a < 1 λ(t) монотонно убывает). P(t) ≈ l – λ 0 ta при λ 0 ta <<1

Нормальный закон распределения. Так как время "жизни" является положительной величиной, то при использовании нормального закона берут усеченный нормальный закон при t > О P(t) = Со[1/2 – Ф ((t - Т) / σt)], F(t) = 1 -P(t), T = М[Тж], где С 0 = 1/ (1/2 - Ф(Т / σt) f(t) = (C 0 / (√ 2Π σt)) eхр (-(t/T)^(2/2σt 2 ) σt 2 = М[(Тж - T)2] Закон Эрланга. Интерес представляет закон Эрланга, являющийся законом распределения суммы случайных величин, каждая из которых имеет экспоненциальное распределение. f(t) = (t / Т)к -1/ (Т 0 Г(к)) еxp (-t/T 0); Тж = (σ2/к)τ ж; β = σ2/Т 0; Т = к. Т 0; Т 0 = σ2/β. σ2 = к. Т 02;

Методы расчёта надёжности 1) Прикидочный расчёт; 2) Ориентировочные расчёты; 3) Окончательный расчёт. Эти методы применяются на различных этапах проектирования аппаратуры. Этапы единой системы контрольной документации (ЕСКД): v. Техническое задание v. Техническое предложение v. Техническое проектирование v. Изготовление рабочих чертежей Прикидочный расчёт проводится на этапе технического предложения. Надёжности всех элементов принимаются одинаковыми. Ориентировочные расчёты надёжности проводятся на этапе эскизного проектирования. Окончательные расчёты надёжности проводятся на этапе технического проектирования, когда становятся известны все режимы работы.