Основы теории надежности Лекция 27 Законы распределения

Основы теории надежности Лекция № 27 Законы распределения сроков службы до отказа 1

Основные законы распределения сроков службы до отказа: 1. Нормальный закон (Гаусса). 2. Логарифмически – нормальный закон. 3. Экспоненциальный закон. 4. Распределение Релея. 5. Распределение Вейбулла. 6. Гамма-распределение. 7. Распределение Стьюдента. 8. Распределение Коши. 9. Распределение Парето. 10. Распределение Симпсона (треугольное). 11. Равномерное распределение. 2

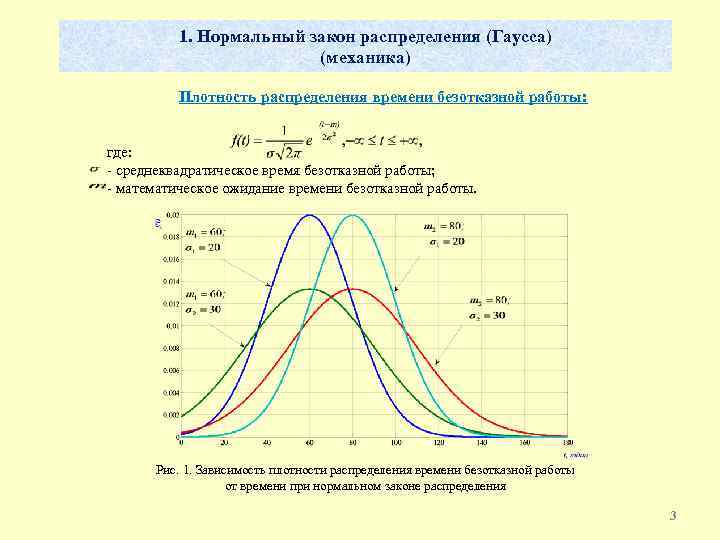1. Нормальный закон распределения (Гаусса) (механика) Плотность распределения времени безотказной работы: где: - среднеквадратическое время безотказной работы; - математическое ожидание времени безотказной работы. Рис. 1. Зависимость плотности распределения времени безотказной работы от времени при нормальном законе распределения 3

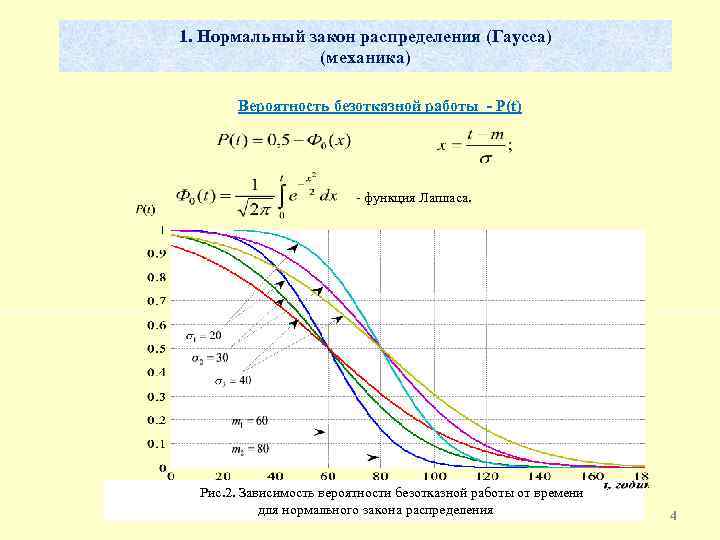1. Нормальный закон распределения (Гаусса) (механика) Вероятность безотказной работы - P(t) - функция Лапласа. Рис. 2. Зависимость вероятности безотказной работы от времени для нормального закона распределения 4

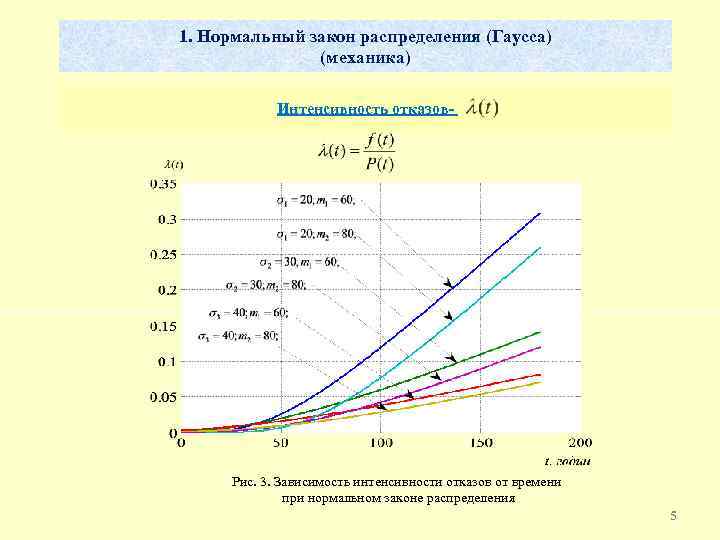1. Нормальный закон распределения (Гаусса) (механика) Интенсивность отказов- Рис. 3. Зависимость интенсивности отказов от времени при нормальном законе распределения 5

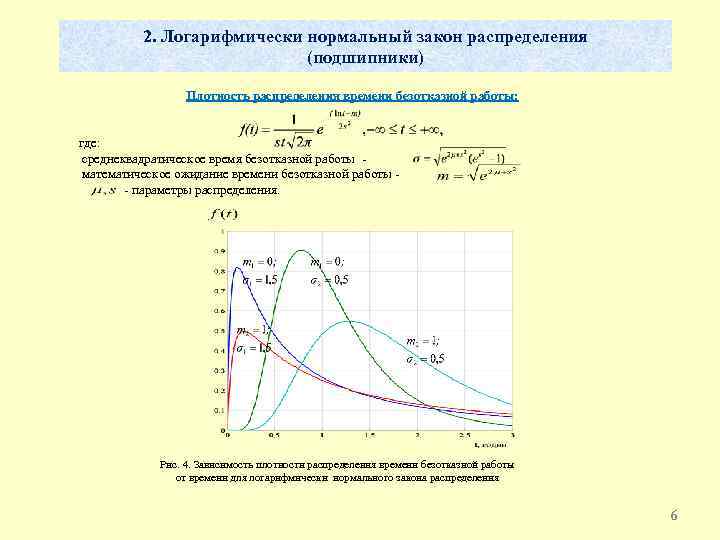2. Логарифмически нормальный закон распределения (подшипники) Плотность распределения времени безотказной работы: где: среднеквадратическое время безотказной работы - математическое ожидание времени безотказной работы - - параметры распределения. Рис. 4. Зависимость плотности распределения времени безотказной работы от времени для логарифмически нормального закона распределения 6

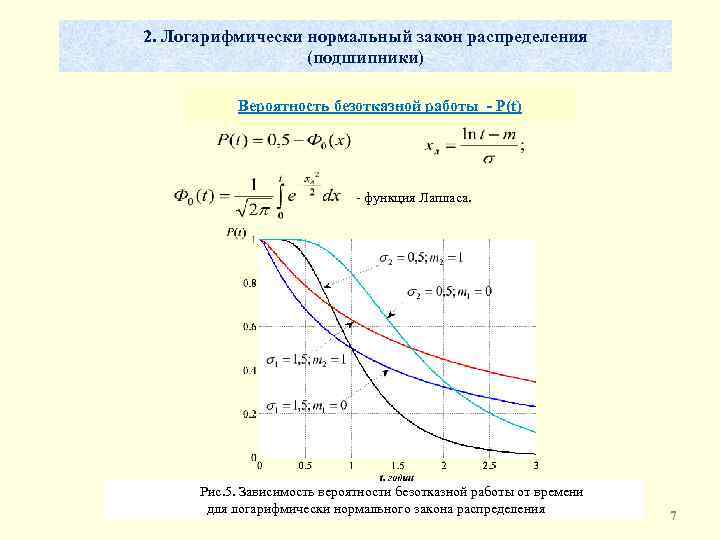2. Логарифмически нормальный закон распределения (подшипники) Вероятность безотказной работы - P(t) - функция Лапласа. Рис. 5. Зависимость вероятности безотказной работы от времени для логарифмически нормального закона распределения 7

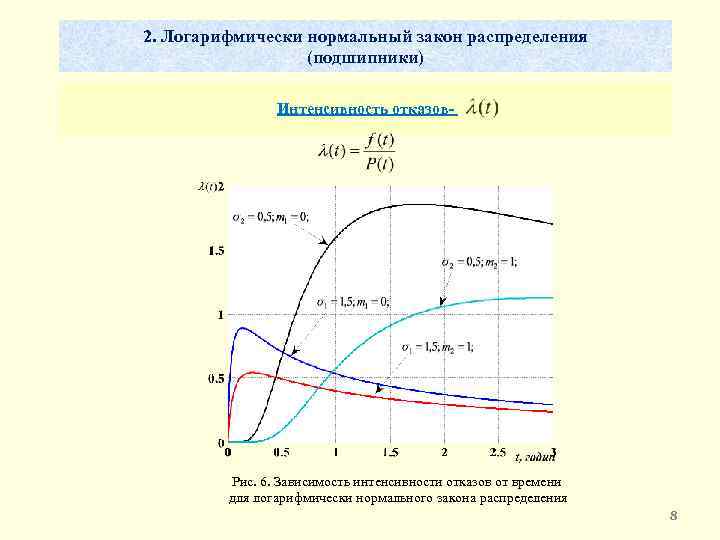2. Логарифмически нормальный закон распределения (подшипники) Интенсивность отказов- Рис. 6. Зависимость интенсивности отказов от времени для логарифмически нормального закона распределения 8

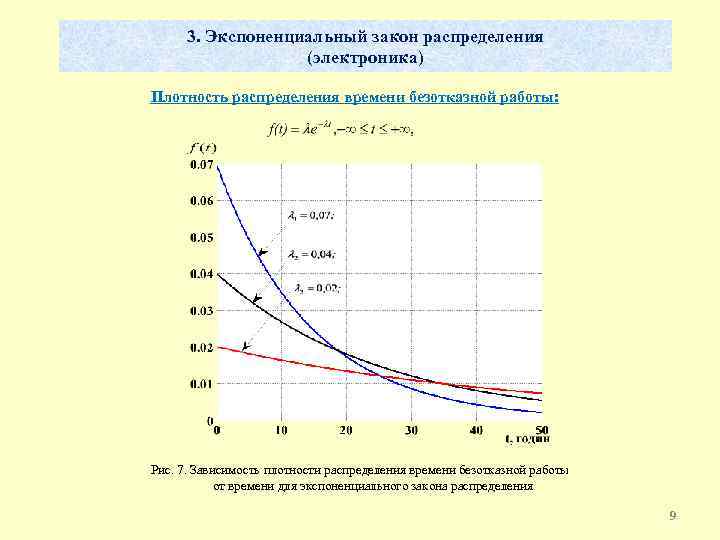3. Экспоненциальный закон распределения (электроника) Плотность распределения времени безотказной работы: Рис. 7. Зависимость плотности распределения времени безотказной работы от времени для экспоненциального закона распределения 9

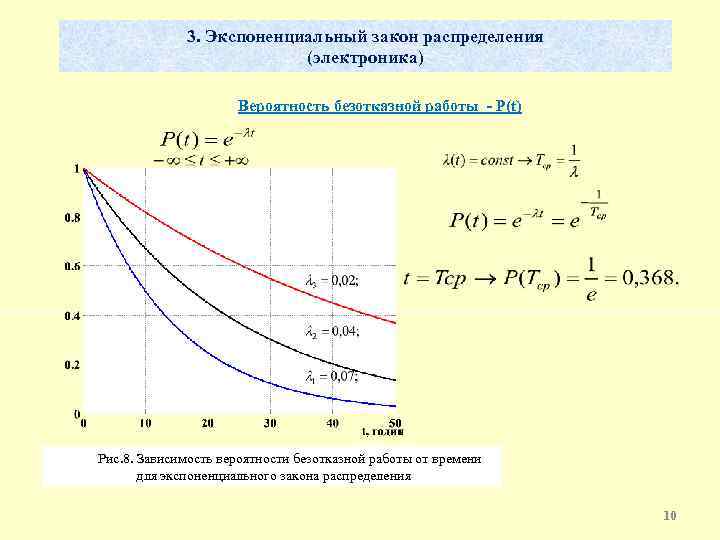3. Экспоненциальный закон распределения (электроника) Вероятность безотказной работы - P(t) Рис. 8. Зависимость вероятности безотказной работы от времени для экспоненциального закона распределения 10

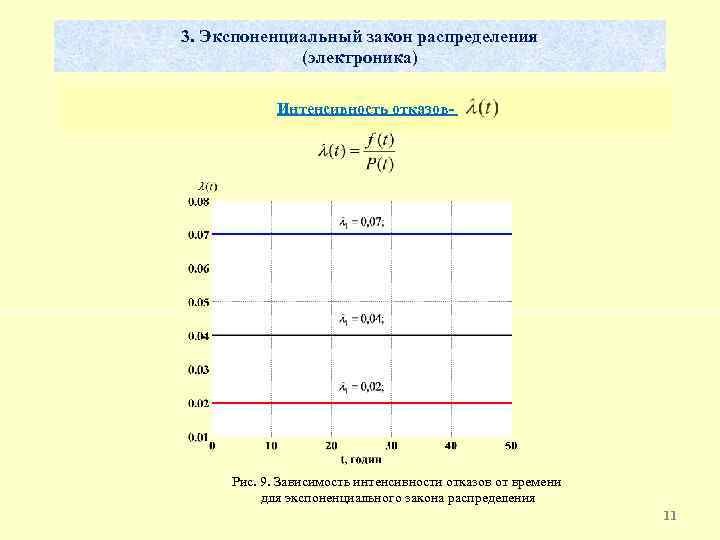3. Экспоненциальный закон распределения (электроника) Интенсивность отказов- Рис. 9. Зависимость интенсивности отказов от времени для экспоненциального закона распределения 11

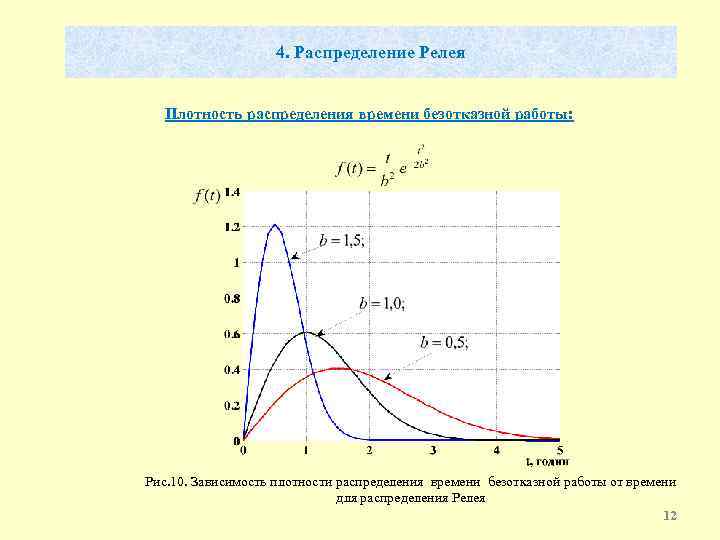4. Распределение Релея Плотность распределения времени безотказной работы: Рис. 10. Зависимость плотности распределения времени безотказной работы от времени для распределения Релея 12

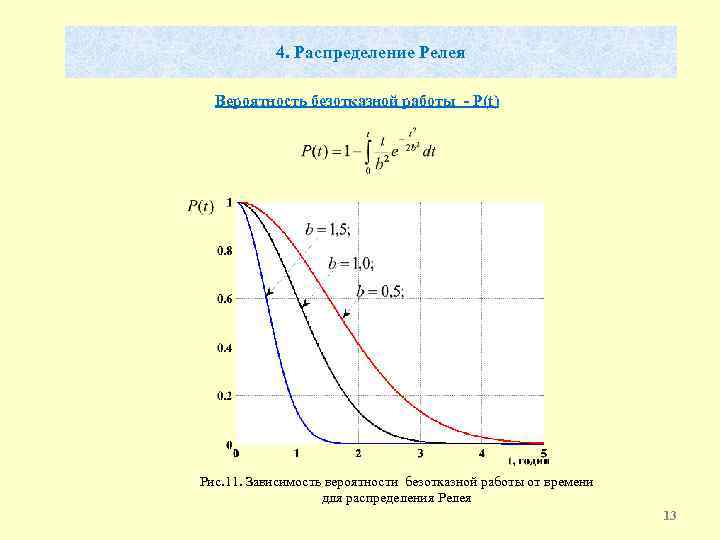4. Распределение Релея Вероятность безотказной работы - P(t) Рис. 11. Зависимость вероятности безотказной работы от времени для распределения Релея 13

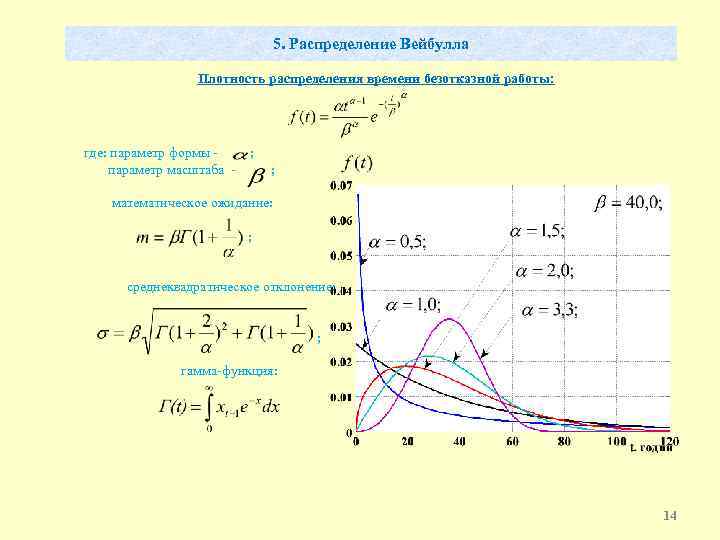5. Распределение Вейбулла Плотность распределения времени безотказной работы: где: параметр формы - ; параметр масштаба - ; математическое ожидание: ; среднеквадратическое отклонение: ; гамма-функция: 14

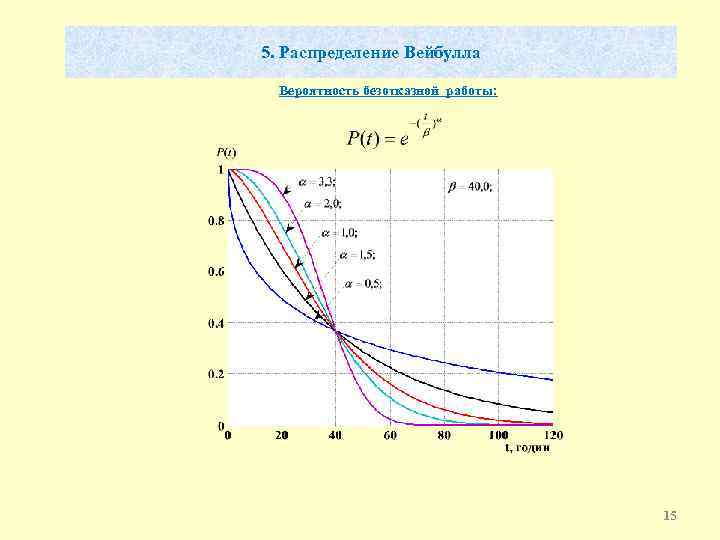5. Распределение Вейбулла Вероятность безотказной работы: 15

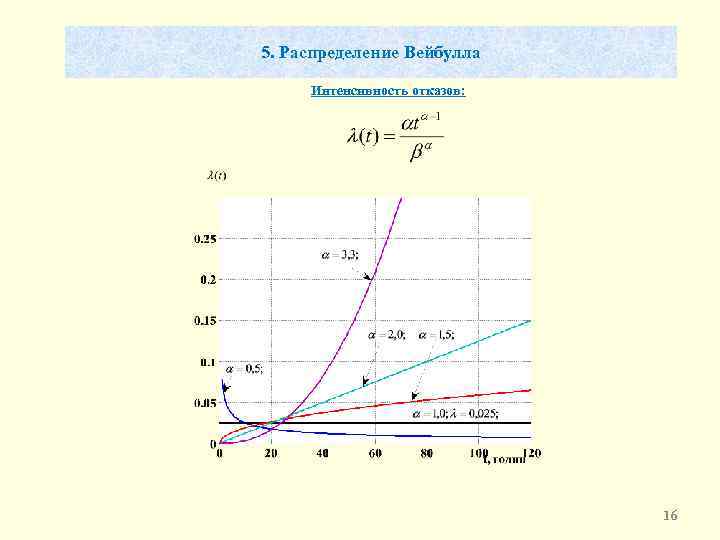5. Распределение Вейбулла Интенсивность отказов: 16

5. Распределение Вейбулла Среднее время безотказной работы: Универсальность распределения Вейбулла: 1. При - распределение Вейбулла превращается в экспоненциальное; 2. При - функции плотности распределения и интенсивности отказов - убывающие; 3. При - функция интенсивности отказов - возрастающая; 4. При - распределение Вейбулла превращается в распределение Релея; 5. При - распределение Вейбулла близко к нормальному. 17

6. Гамма – распределение Плотность распределения времени безотказной работы: Вероятность безотказной работы: Математическое ожидание и среднеквадратическое отклонение связаны с параметрами и следующими соотношениями: и . Параметр характеризует асимметрию гамма - распределения и определяет вид характеристик надежности. При интенсивность отказов убывает. При интенсивность отказов возрастает. При интенсивность отказов постоянна, т. е. гамма – распределение превращается в экспоненциальное. 18

Композиция законов распределения: Для несколько случайных величин , с плотностями распределения Закон распределения случайно величины называется композицией законов распределения величин - . Плотность распределения величины - является композицией распределений Композиция может существовать для любого числа случайных величин. Композиция законов распределения имеет ряд общих и частных свойств. Общие свойства не зависят от вида рассматриваемого закона распределения, а частные применимы только к определенным законам распределения. Общие свойства композиции законов распределения: Математическое ожидание композиции распределения равно сумме математических ожиданий независимых случайных величин, образующих сложную случайную величину: Дисперсия композиции распределения равно сумме дисперсий независимых случайных величин, образующих сложную случайную величину: Частные свойства композиции законов распределения: Композиция распределений Пуассона дает только распределение Пуассона при любом количестве распределений. Композиция нормальных распределений дает только нормальное распределение при любом количестве распределений. Композиция экспоненциальных распределений дает новое гамма-распределение. 19

Контрольные вопросы по теме лекции № 9: 1. 2. 3. 4. 5. 6. 7. 8. Основные законы распределения сроков службы до отказа. Определение основных критериев надежности при нормальном законе распределения. Определение основных критериев надежности при логарифмически нормальном законе распределения. Определение основных критериев надежности при экспоненциальном законе распределения. Определение основных критериев надежности при распределении Релея. Определение основных критериев надежности при распределения Вейбулла. Определение основных критериев надежности при гамма - распределении. Композиция законов распределения. Общие и частные свойства композиции законов распределения. 20