Основы теории информации Информация Свойства информации

Основы теории информации

Информация. Свойства информации

Теория информации - это раздел математики, исследующий различные формы информации и процессы её хранения, преобразования и передачи. Теория информации тесно связана с криптографией.

Основоположником теории информации считается американский инженер и математик Клод Элвуд Шеннон.

Информация – это совокупность сведений, подлежащих хранению, передаче, обработке и использованию в человеческой деятельности. Сведения — это знания, выраженные в сигналах, сообщениях, известиях, уведомлениях либо иной форме. Информацию, представленную в формализованном виде, позволяющем осуществлять ее обработку с помощью технических средств, называют данными.

Информация может быть представлена в аналоговой форме, в цифровой – в виде двоичнокодированных чисел либо алфавитно-цифровых кодов или в командной. Разница между аналоговой информацией и цифровой в том, что аналоговая информация непрерывна, а цифровая дискретна Этапы обращения информации: 1. Восприятие информации (анализ информации о каком-либо объекте, в результате которого формируется образ объекта, проводится его опознание и оценка);

2. 3. 4. 5. 6. Подготовка информации (получение сигнала в форме, удобной для передачи или обработки (аналого-цифровое преобразование и пр. )); Передача и хранение информации; Обработка информации (выделение общих и существенных взаимосвязей для выбора управляющих воздействий); Отображение информации (представление информации в форме, способной воздействовать на органы чувств человека); Воздействие информации (осуществляются необходимые изменения в системе).

Свойства информации: 1. Объективность информации характеризует её независимость от чьего-либо мнения, а также от методов получения. 2. Полнота - информацию можно считать полной, когда она содержит минимальный, но достаточный для принятия правильного решения набор сведений. 3. Достоверность - верность информации, не вызывающая сомнений. 4. Адекватность – степень соответствия смысла реально полученной информации и её ожидаемого содержимого.

5. 6. Доступность информации мера возможности получить ту или иную информацию. Актуальность информации - это степень соответствия информации текущему моменту времени.

Информационные системы

Информационной системой называется комплекс, включающий вычислительное и коммуникационное оборудование, программное обеспечение, информационные ресурсы, а также системный персонал и обеспечивающий удовлетворение информационных потребностей пользователей. Автоматизированными называют ИС, в которых применяются технические средства, в частности ЭВМ.

Классификации ИС: 1. По степени распределенности: настольные (desktop), или локальные ИС, в которых все компоненты (БД, СУБД, клиентские приложения) находятся на одном компьютере; распределённые (distributed) ИС, в которых компоненты распределены по нескольким компьютерам.

Распределённые ИС, в свою очередь, разделяют на: файл-серверные ИС; клиент-серверные ИС.

По степени автоматизации: автоматизированные ИС, в которых автоматизация может быть неполной (то есть требуется постоянное вмешательство персонала); автоматические ИС, в которых автоматизация является полной, то есть вмешательство персонала не требуется или требуется только эпизодически. 3. По характеру обработки данных: 2.

информационно-справочные, или информационно-поисковые ИС, в которых нет сложных алгоритмов обработки данных, а целью системы является поиск и выдача информации в удобном виде; ИС обработки данных, или решающие ИС, в которых данные подвергаются обработке по сложным алгоритмам. К таким системам относят автоматизированные системы управления и системы поддержки принятия решений.

4. 5. По сфере применения По охвату задач (масштабности): персональная ИС предназначена для решения некоторого круга задач одного человека. групповая ИС ориентирована на коллективное использование информации членами рабочей группы или подразделения. корпоративная ИС охватывает все информационные процессы целого предприятия, достигая их полной согласованности.

Носитель информации. Сигнал. Сообщение

Материальным носителем называют материальный объект или среду, которые служат для представления или передачи информации. Материальными носителями информации могут быть: бумага, воздух, электромагнитное поле и т. п. Сигнал — материальный носитель информации, используемый для передачи сообщений в системе связи.

Сигналом является изменение некоторой характеристики носителя с течением времени. Значение этой характеристики, отнесенное к некоторой шкале измерений, называется параметром сигнала (способ передачи – компьютерная сеть, процесс – электрический ток, параметр сигнала – частота и амплитуда электрических колебаний в линии связи).

Ширина частотного спектра (Fs) – диапазон частот, в пределах которого находится наиболее существенная часть спектра сигнала. Она определяет скорость изменения сигнала внутри интервала его существования. Спектр сигнала может быть неограниченным. В технике связи спектр сигнала часто сознательно сокращают, т. к. аппаратура и линия связи имеют ограниченную полосу пропускаемых частот.

Выделяют два типа сигналов: 1. Аналоговый (непрерывный) сигнал – это зависящие от времени ток или напряжение, которые непрерывно изменятся по определенному закону. Аналоговый сигнал принимает бесконечное множество значений в пределах динамического диапазона. Примерами непрерывных сигналов являются речь и музыка, изображение, показание термометра (параметр сигнала – высота столба спирта или ртути – имеет непрерывный ряд значений)

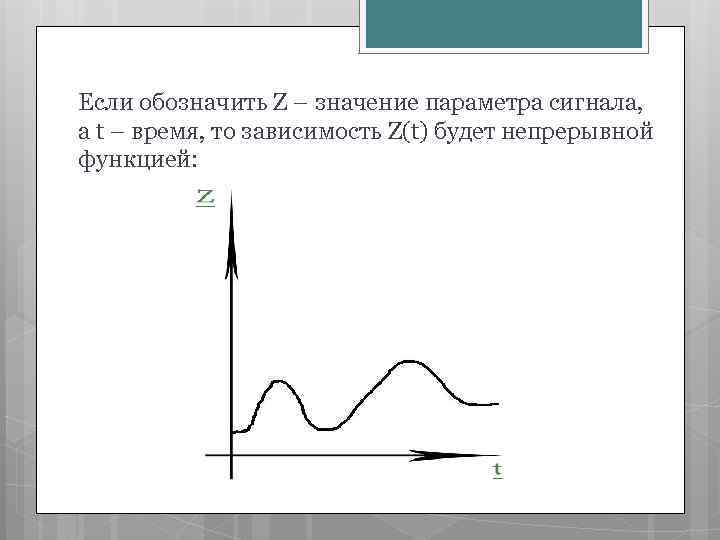Если обозначить Z – значение параметра сигнала, а t – время, то зависимость Z(t) будет непрерывной функцией:

Цифровой (дискретный) сигнал – это коды, которые соответствуют дискретным отсчетам и уровням квантования аналоговых сигналов (квантование - разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов). Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала. Примерами устройств, использующих дискретные сигналы, являются часы (электронные и механические), цифровые измерительные приборы, книги, табло и пр. 2.

Дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров Z

Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т. е. приписать каждому из конечного числа возможных значений сигнала знак, который будет отличать данный сигнал от другого. Знак – это элемент некоторого конечного множества отличных друг от друга сущностей. Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков или дискретным множеством знаков.

Набор знаков, в котором установлен порядок их следования, называется алфавитом. Алфавит содержит минимум два знака – такой алфавит называется двоичным.

Для передачи информации используется ряд следующих друг за другом сигналов, называемых сообщением. Сообщение – это информация, выраженная в определенной форме и подлежащая передаче. От источника к приемнику информация передается в виде сообщений. Сообщение выступает в качестве материальной оболочки для представления информации при передаче. Следовательно, сообщение служит переносчиком информации, а информация является содержанием сообщения. Соответствие между сообщением и содержащейся в нем информацией называется правилом интерпретации сообщения.

Это соответствие может быть однозначным и неоднозначным. При однозначном соответствии сообщение имеет лишь одно правило интерпретации. Неоднозначность соответствия между сообщением и информацией возможна в двух вариантах: одна и та же информация может передаваться различными сообщениями (например, прогноз погоды может быть получен по радио, из газеты, по телефону и пр. );

одно и то же сообщение может содержать различную информацию для разных приемников Решающим фактором для извлечения информации из сообщения является знание языка сообщения или способа его кодирования.

Информационные процессы

Информационный процесс – это изменение с течением времени содержания информации или представляющего сообщения. Два типа информационных процессов: 1. Изменение сообщения с сохранением содержащейся в нем информации (передача информации без потерь и обратимая перекодировка); 2. Изменение сообщения, сопровождающееся преобразованием информации (созданиеуничтожение, необратимая перекодировка, передача с потерями, обработка с появлением новой информации).

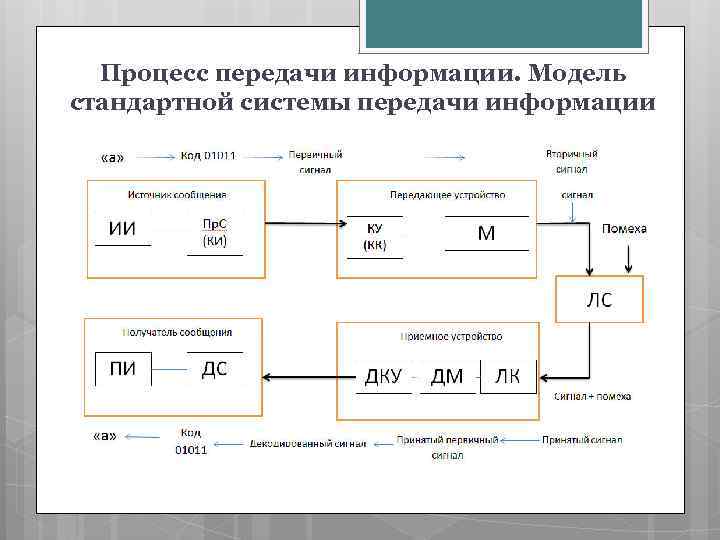Процесс передачи информации. Модель стандартной системы передачи информации

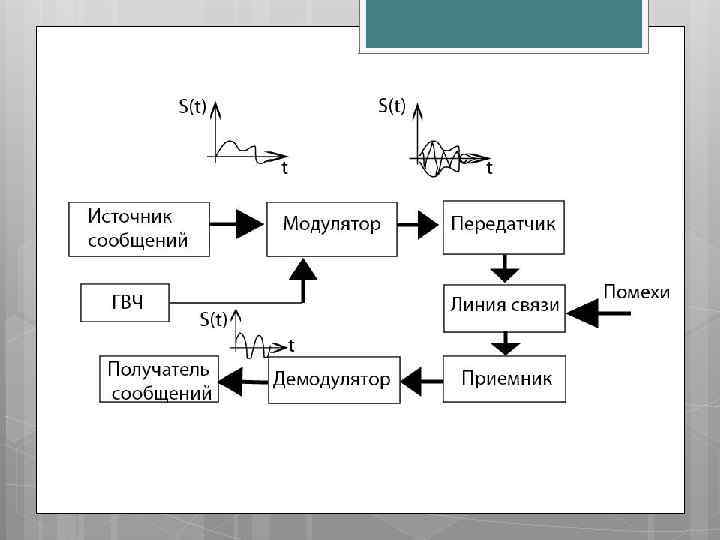
Система передачи информации – совокупность технических средств (передатчик, приемник, линия связи), обеспечивающих возможность передачи сообщений от источника к получателю. Источник сообщения в общем случае образует совокупность источника информации (исследуемого или наблюдаемого объекта) и преобразователя сообщений. Источником информации (ИИ) могут быть люди, технические устройства, а также терминалы под управлением операторов и других устройств.

Преобразователь сообщений (Пр. С) – выполняет две функции: первая – преобразование сообщения любой физической природы в первичный электрический сигнал; вторая – преобразование большого объема алфавита сообщений в малый объем алфавита первичного сигнала (кодирование). Из-за того, что Пр. С выполняет две функции его иногда называют кодером источника (КИ). Передающее устройство осуществляет преобразование сообщений в сигналы, удобные для прохождения по конкретной линии связи. В его состав может входить устройство, обеспечивающее помехоустойчивое кодирование – кодирующее устройство (КУ), или кодер канала (КК).

Первичный электрический сигнал непосредственно не передается по линиям связи. В передатчике первичный сигнал преобразуется во вторичный (высокочастотный) сигнал, пригодный для передачи по линии связи. Такое преобразование осуществляется посредством модулятора (М), который изменяет один из параметров высокочастотного колебания в соответствии с изменением первичного сигнала. Линия связи (ЛС) – это физическая среда, которая связывает между собой передатчик и приемник. Сигналы на выходе линии связи могут отличаться от сигналов на ее входе вследствие затухания, искажения и воздействия помех.

Помехой называют любые мешающие возмущения, как внешние, так и внутренние, вызывающие отклонения принятых сигналов от переданных сигналов. Приемное устройство обрабатывает зашумленный сигнал: отделяет полезный сигнал от помехи и восстанавливает по нему переданное сообщение. Принимаемый полезный высокочастотный сигнал фильтруется и усиливается линейным каскадом (ЛК) приемного устройства и поступает на демодулятор (ДМ), в котором высокочастотный сигнал преобразуется в низкочастотный первичный сигнал.

В декодирующем устройстве (ДКУ) низкочастотный сигнал преобразуется в кодовую комбинацию символов первичного сигнала. Одновременно ДКУ обнаруживает и исправляет искаженные символы первичного сигнала. На выходе ДКУ имеется кодовая комбинация символов первичного сигнала, соответствующая передаваемому сообщению. Детектор сигнала (ДС) преобразует кодовую комбинацию символов первичного сигнала в соответствующее сообщение, которое поступает на вход получателя информации (ПИ), которому была адресована исходная информация.

Каналы связи

Понятие канал связи включает в себя материальную среду, а также физический или иной процесс, посредством которого осуществляется передача сообщений, т. е. распространение сигналов в пространстве с течением времени (например: канал связи – компьютерные сети, среда – проводник, носитель информации – электрический ток, процесс, используемый для передачи сообщений – перемещение электрических зарядов).

В каналах связи используется четыре режима передачи данных: 1. Симплексный, когда сигнал передается только в одном; 2. Полудуплексный, передача данных может осуществляться в обоих направлениях, но не одновременно; 3. Дуплексный, характеризуется передачей данных в обоих направлениях, но только между двумя пунктами;

4. Расширенный дуплексный режим, передача данных возможна одновременно в обоих направлениях, но между различными пунктами, т. е. один абонент передает информацию второму и одновременно получает информацию от третьего. Возможен только в многоканальных системах связи.

Параметры канала связи: 1. Ширина полосы пропускания – интервал частот, используемых данным каналом связи для передачи сигналов. Наиболее важна не сама ширина полосы пропускания, а максимальное значение частоты из данной полосы, поскольку именно ей определяется возможная скорость передачи информации по каналу. 2. Пропускная способность (С) - среднее количество информации, передаваемое по каналу за единицу времени. Количество информации выражается в битах, а длительность сигнала – в секундах, то единицей измерения C будет бит/с. Помехи приводят к снижению пропускной способности канала.

Бит в секунду – базовая единица измерения скорости передачи информации. Более крупная единица — байт в секунду равная 8 бит/c. Для обозначения больших скоростей передачи применяют более крупные единицы, образованные с помощью приставок кило-, мега-, гига- : Килобиты в секунду — Кбит/c (Kbps) Мегабиты в секунду — Мбит/c (Mbps) Гигабиты в секунду — Гбит/c (Gbps) 1 кило- в данном случае равняется 1024. Например, 8 Кбит/c = 8192 бит/с = 1 КБ/c.

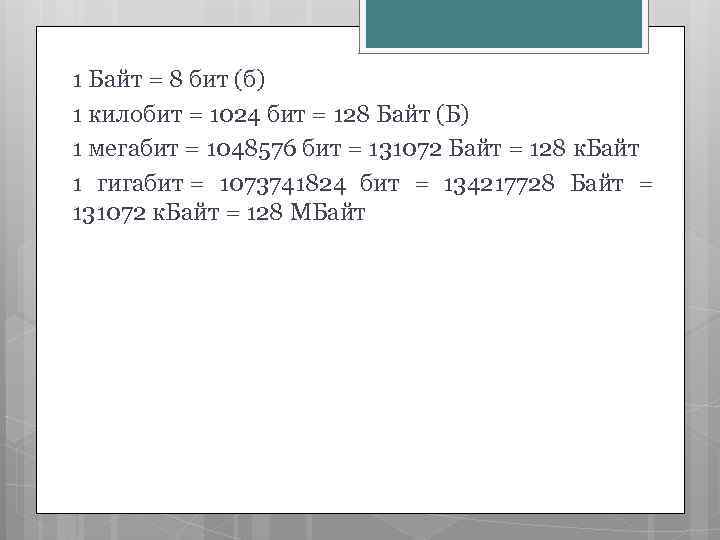1 Байт = 8 бит (б) 1 килобит = 1024 бит = 128 Байт (Б) 1 мегабит = 1048576 бит = 131072 Байт = 128 к. Байт 1 гигабит = 1073741824 бит = 134217728 Байт = 131072 к. Байт = 128 МБайт

3. Скорость передачи информации – величина, характеризующая быстроту передачи информации (J). Измеряется в бит/с. Максимальная скорость передачи информации по каналу связи равна его пропускной способности.

Дискретный канал связи – это совокупность средств, предназначенных для передачи цифровых сигналов. На вход такого канала подаются дискретные сообщения, которые преобразуются в кодированные сигналы. В дискретном канале связи без помех каждому входному сигналу соответствует тот же сигнал на выходе. Эти сигналы связана однозначной зависимостью.

Непрерывный канал связи – это совокупность средств, предназначенных для передачи непрерывных сигналов. Для описания непрерывных сигналов используются средние статистические характеристики: среднее значение случайной величины (математическое ожидание), дисперсия (мера разброса случайной величины относительно среднего значения), корреляционная функция (степень взаимной зависимости случайных значений процесса в разные моменты времени), функция плотности распределения вероятностей, интегральная функция распределения вероятностей.

Линии связи Составной частью любого канала передачи информации является линия связи – физическая среда, обеспечивающая поступление сигналов от передающего устройства к приемному. В зависимости от среды линии связи делятся: на проводные (воздушные); кабельные (медные и волоконно-оптические); беспроводные (наземной и спутниковой связи). Проводная линия связи представляет собой проложенные между опорами провода без какихлибо экранирующих или изолирующих оплеток. Помехозащищенность и скорость передачи данных в этих линиях низкая (пример: телефонные линии).

Кабельные линии связи представляют собой пучок проводов, заключенных в одну или несколько защитных трубок. Важнейшими параметрам кабеля являются: максимальное затухание передаваемого сигнала на разных частотах и задержка распространения сигнала в кабеле на единицу длины. В современных системах связи применяют кабели двух типов:

На основе витых пар медных проводов – отличаются способностью снижать влияние внешних помех на сигналы, передаваемые по кабелю. Конструктивно витая пара может быть неэкранированной и экранированной. В кабелях с экранированной витой парой каждая витая пара помещается в металлическую оплетку (экран) для уменьшения излучений кабеля, защиты от внешних электромагнитных помех и снижения влияния пар проводов друг на друга. В процессе эксплуатации необходимо применять специальные экранированные разъемы. Достоинство неэкранированной витой пары – простота монтажа разъемов на концах кабеля, простота ремонта любых повреждений.

Волоконно-оптический кабель – представляет собой проводник света и состоит из сердцевины (стеклянного волокна), стеклянной оболочки, обладающей меньшим коэффициентом преломления, чем сердцевина, и внешней оболочки. Свет распространяется в результате полного внутреннего отражения от границы раздела сердцевины и стеклянной оболочки. Позволяют передавать информацию на большие расстояния с более высокой скоростью передачи данных.

Беспроводные линии связи – различаются радиусом действия, поддерживаемыми скоростями передачи данных и технологией кодирования данных. Наиболее распространенным является протокол беспроводной сети IEEE 802. 11 (стандарт 802. 11 b/g).

Помехи в линиях связи По форме помехи делятся на несколько видов: Синусоидальные – от промышленной сети с частотой 50 Гц, от медицинских установок и различных аппаратов; Импульсные – в виде отдельных импульсов или групп импульсов (помехи от систем зажигания двигателей внутреннего сгорания); Хаотические – типа теплового шума (броуновское движение заряженных частиц). По характеру мешающего воздействия помехи делятся на: Аддитивные – когда в канале связи помеха складывается с полезным сигналом;

Мультипликативные – когда воздействие помехи эквивалентно изменению коэффициента передачи канала связи. Аддитивные помехи подразделяются на: Помехи соседних радиоканалов (перекрестные помехи) – возникают из-за перекрытия спектров соседних каналов связи; Промышленные помехи (искусственные помехи) – возникают вследствие затухания затухающих колебаний при искрообразовании в различных электрических устройствах; Флуктуационные помехи – источником являются внутренние шумы, представляют собой случайные колебания токов и напряжений в элементах радиоаппаратуры.

Помехи в виде случайного процесса – нежелательный процесс, который сопровождает передачу сигналов в линиях связи. Часть помех в линии связи вносят электронные компоненты – различные шумы: тепловой, (возникает в процессе теплового возбуждения атомов проводника или резистора; в результате появляются свободные электроны, движение которых приводит к появлению случайной разности потенциалов на концах проводника или резистора), дробовой (присутствует везде, где через какое-либо активное устройство течет постоянный или переменный ток и происходят случайные колебания величины этого тока, которые накладываются на сигнал и искажают его),

Аналоговые системы передачи информации На начальном этапе развития системы передачи информации были только аналогового типа, так как большинство физических источников информации (микрофоны, датчики) вырабатывали аналоговый сигнал, а задача системы передачи информации – перенести этот сигнал на заданное расстояние. Аналоговые системы передачи информации (АСПИ) менее помехоустойчивы по сравнению с цифровыми системами.

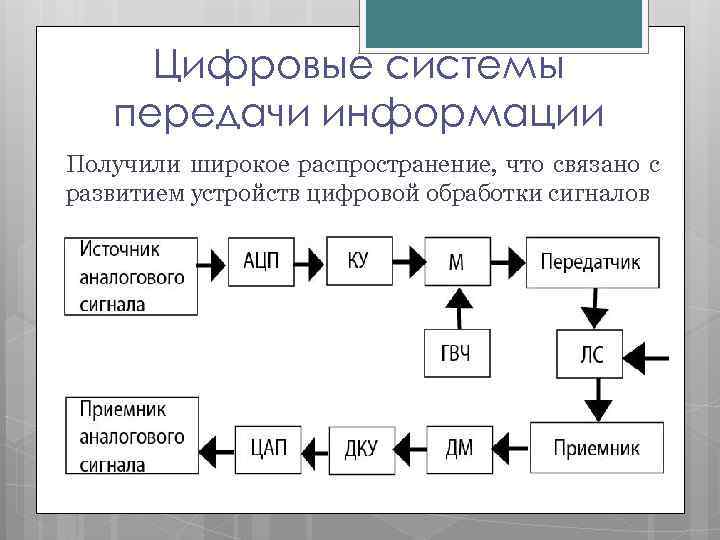Цифровые системы передачи информации Получили широкое распространение, что связано с развитием устройств цифровой обработки сигналов

В структурную схему ЦСПИ включается аналогоцифровой преобразователь (АЦП) и КУ, в котором выполняется помехоустойчивое кодирование. Модулятор передатчика выполняет вторичную модуляцию колебаний с ГВЧ. На входе приемника стоит ДМ, который извлекает информацию из параметра передаваемого по ЛС несущего колебания. С помощью ДКУ извлекается информация из импульсной последовательности, а цифро-аналоговый преобразователь (ЦАП) формирует аналоговый сигнал. ЦСПИ характеризуются высокой помехоустойчивостью и широкими функциональными возможностями. Цифровые сигналы менее аналоговых восприимчивы к помехам,

обусловленным шумами, так как при цифровой передаче для опознания логического состояния сигналов нет необходимости в точной оценке амплитуды, частоты или фазы. Цифровые сигналы более удобны для обработки и хранения, а скорость их передачи проще адаптировать к окружению и стыковать с различными типами оборудования.

Способы преобразования сообщений Между непрерывными и дискретными сообщениями возможны четыре вида преобразований:

Примером устройств, в которых осуществляется преобразование типа N 1 N 2, является микрофон (звук преобразуется в электрические сигналы); телекамера (изображение и звук превращаются в электрические сигналы) и т. п. Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации. Потери связаны с помехами, которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину.

В ряде устройств искажение происходит в силу особенностей преобразования в них сообщений (например телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса). С математической точки зрения перевод сигнала из аналоговой формы в дискретную означает замену описывающей его непрерывной функции времени Z(t) на некотором отрезке [t 1, t 2] конечным множеством (массивом) {Zi, ti} (i=0…n, где n – количество точек разбиения временного интервала). Такое преобразование называется дискретизацией непрерывного сигнала и осуществляется посредством двух операций: развертки по времени и квантования по величине сигнала.

Развертка по времени состоит в том, что наблюдение за изменением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом t. Квантование по величине – это отображение вещественных значений параметра сигнала в конечное множество чисел, кратных некоторой постоянной величине – шагу квантования ( Z). Совместное выполнение обоих операций эквивалентно нанесению масштабной сетки на график Z(t).

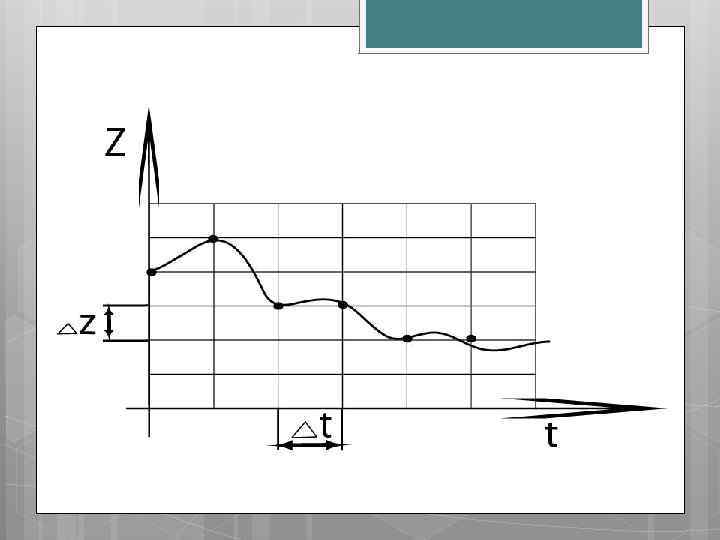
Далее, в качестве пар значений {Zi, ti} выбираются узлы сетки, расположенные наиболее близко к Z(ti). Полученное таким образом множество узлов оказывается дискретным представлением исходной непрерывной функции. Любое сообщение, связанное с ходом Z(t), может быть преобразовано в дискретное, т. е. представлено посредством некоторого алфавита. При такой замене очевидно, что чем меньше n (больше t), тем меньше узлов, но и точность замены Z(t) значениями Zi будет меньше. При дискретизации может происходить потеря части информации, связанная с особенностями функции Z(t).

Теорема Отсчетов: Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале (теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы; любое подобное устройство использует не весь спектр частот колебаний, а лишь какую-то его часть и согласно теореме отсчетов определяющим является значение верхней границы частоты (Vm)). Дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью

восстановить исходный аналоговый сигнал, если развертка по времени будет выполнена в соответствии со следующим соотношением: (1) Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать t, определяемый в соответствии с формулой 1.

Например: для точной передачи речевого сигнала с частотой до Vm = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду, а временной интервал наблюдений составит 0, 000125 с. Шаг квантования определяется чувствительностью приемного устройства. Указанные рекомендации по выбору шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, лазерный проигрыватель и т. п. Термины «цифровая запись» , «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита

Преобразование сигналов типа N D и обратное D N может осуществляться без потери содержащейся в них информации. Преобразование типа D 1 D 2 состоит в переходе при представлении сигналов от одного алфавита к другому – такая операция называется перекодировка и может осуществляться без потерь. Пример: шифровка и дешифровка текста, вычисления на калькуляторе. Преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другим достоинствам дискретной формы сообщений относят:

высокую помехоустойчивость; простоту и надежность устройств по обработке информации; точность обработки информации; универсальность устройств. Универсальность обусловлена тем, что любые дискретные сообщения, составленные в различных алфавитах, посредством обратимого кодирования можно привести к единому алфавиту. Это позволяет выделить некоторый алфавит в качестве базового и представлять в нем любую дискретную информацию. Тогда устройство, работающее с информацией в базовом алфавите, оказывается универсальным в том отношении, что оно может быть использовано для переработки любой иной исходной дискретной

информации. Базовым алфавитом является двоичный, а использующим его универсальным устройством – компьютер.

Вероятностный подход к определению количества информации Наиболее известным и широко применяемым на практике является вероятностный подход к измерению информации. Математическим аппаратом вероятностной теории информации является теория вероятностей. Любые действия, приводящие к появлению некоторого события, принятию величиной некоторого значения, называются в вероятностной теории опытом. Считается, что до осуществления опыта известно все множество его исходов, но не известно, каким из этих исходов он закончится.

По окончании опыта неопределенность относительно его результата или совсем исчезает, или уменьшается. Уменьшение неопределенности касательно исхода опыта в результате его осуществления понимается в вероятностной теории как получение информации. Энтропия конечного множества случайных событий Имеется конечное множество Х случайных событий х1, х2, …, х. N, которые могут произойти в некотором опыте. Эти события независимы и несовместны и известны вероятности p(x 1)=p 1, …, p(x. N)=p. N их осуществления в опыте. Они образуют полную группу событий: p 1+p 2+…+p. N=1.

1. 3. Если вероятности всех событий, кроме одного, равны 0, а этого единственного – единице, то H(X) = 0 (в данном случаев любом опыте с множеством Х результат известен заранее и неопределенность в исходе опыта отсутствует). Энтропия максимальна, если все события множества равновероятны (этом случае исход опыта наиболее неопределенен). Н(Х)max = log N.

Количество информации, получаемое в опыте с конечным множеством случайных событий За меру количества информации в вероятностной теории принята разность неопределенностей исхода опыта до и после его осуществления. Опыты, проводимые с множеством событий, делятся на 2 категории. К первой относятся такие, которых наблюдаемые события всегда признаются за истинные, достоверные, действительно осуществившиеся в опыте. Во вторую категорию опытов входят такие, в которых наблюдаемые события являются лишь отражением тех истинных событий, которые действительно имеют место в опыте.

Алфавитный подход к измерению информации - позволяет определить количество информации, заключенной в тексте. Алфавитный подход является объективным, т. е. он не зависит от субъекта (человека), воспринимающего текст. Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:

Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен: I = К * i, где i — информационный вес одного символа в используемом алфавите, К- количество символов в тексте, I – количество информации, содержащейся в тексте (информационный объем текста).

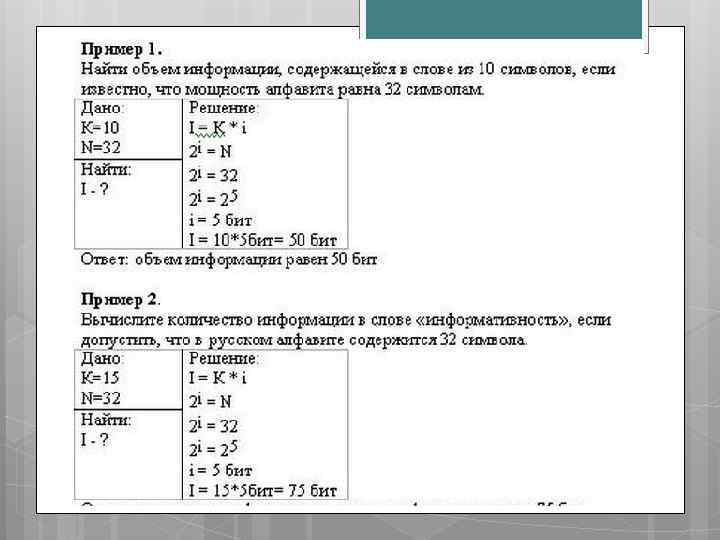
При алфавитном подходе к измерению информации ее количество не зависит от содержания, а зависит от мощности алфавита и количества символов в тексте. Правило для измерения информации с точки зрения алфавитного подхода: 1) Найти мощность алфавита – N 2) Найти информационный вес одного символа i из уравнения 3) Найти количество символов в тексте - К 4) Найти количество информации – I

Например: Книга, набранная с помощью компьютера содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге? Решение. Мощность компьютерного алфавита равна 256. Один символ несет 1 байт информации. Значит, страница содержит 40*60=2400 байт информации. Объем всей информации в книге равен: 2 400*150=360 000 байт

Вычислить количество информации, содержащейся во фразе «экзамен сдан» , если мощность алфавита составляет 32 символа. Вычислить количество информации, содержащейся в слове «сигнал» , если известно, что вес одного символа равен 4. Найти информационный объем слова 5 букв, если известно, что мощность алфавита составляет 64 символа.

Вероятностные дискретные источники В вероятностной теории информации рассматриваются дискретные источники со случайным характером выдачи элементов. Источники, вырабатывающие случайные последовательности элементов, называются вероятностными дискретными источниками (ВДИ). Элементы последовательности, выдаваемой ВДИ, могут быть статистически независимы и зависимы. Если значение элемента зависит в статистическом смысле от значения ранее выданных элементов, то такой источник называется источником с памятью.

Скорость выдачи информации источником называется производительностью источника. Чем больше I(XT), тем большей производительностью обладает источник. Производительность – важнейшая характеристика источника. Максимальная производительность источника, характеризуя его потенциальные возможности, не определяет той истинной производительности, которую он имеет. Это лишь предельно достижимая производительность источника.

Избыточность последовательности, выдаваемой ВДИ

Изменение избыточности путем кодирования http: //www. technofresh. ru/technology/poligon/cryptography-1. html Операциями, позволяющими изменять избыточность информации, выдаваемой ВДИ, являются кодирование 2 и 3 -го типов. Под кодированием информации понимается установление взаимнооднозначного соответствия между отрезками последовательности, выдаваемой ВДИ, и некоторыми другими ограниченными по длине последовательностями элементов из конечного алфавита Z мощности m=|Z|. Элементы указанного алфавита будут называться символами, а последовательности этих элементов, используемые при кодировании – кодовыми комбинациями.

Все множество Y кодовых комбинаций, применяемое при кодировании, называется кодом, а преобразователи, выполняющие указанные операции, - кодерами. Для кодирования отрезков конечной длины последовательности применяют блоковые коды. Код называется блоковым, если каждая его комбинация имеет ограниченную длину. БК делятся на равномерные и неравномерные. Код называется равномерным, если все его комбинации имеют одну и ту же длину, и неравномерным – если длины его комбинаций различны.

Например: пятисимвольный двоичный блоковый код является равномерным, т. к. каждая его комбинация состоит из пяти двоичных символов, а код Морзе является неравномерным, т. к. используемые в нем комбинации при кодировании букв содержат от 1 до 4 двоичных символов, при кодировании цифр – 5 двоичных символов, при кодировании знаков препинания – 6 двоичных символов. Неравномерные коды подразделяют на коды с разделительными и без разделительных знаков. Код называется кодом с разделительными знаками, если однозначное разделение последовательности его комбинаций на отдельные комбинации невозможно осуществить без использования специального знака. Пример – код Морзе.

Код называется кодом без разделительных знаков, если любая последовательность его комбинаций однозначно разделяется на отдельные комбинации без использования специального знака. Код без разделительных знаков может содержать только такие комбинации, которые удовлетворяют условию: ни одна из них в целом не является началом другой. Например, у такой код могут входить комбинации 10 и 001, но не могут 10 и 100, т. к. при появлении в последовательности символов 10 невозможно точно указать, являются ли они комбинацией 10 или первыми символами комбинации 100.

искаженные символы, появляющиеся в его комбинациях в результате действия помех и отказов элементов аппаратуры. Некорректирующим является код, который не позволяет обнаруживать искаженные символы в своих комбинациях. Кодирование, позволяющие уменьшать избыточность, называют эффективным. Его используют для наиболее экономного представления информации. Кодирование, приводящее к увеличению избыточности, называют помехоустойчивым. Его применяют для повышения верности представления информации.

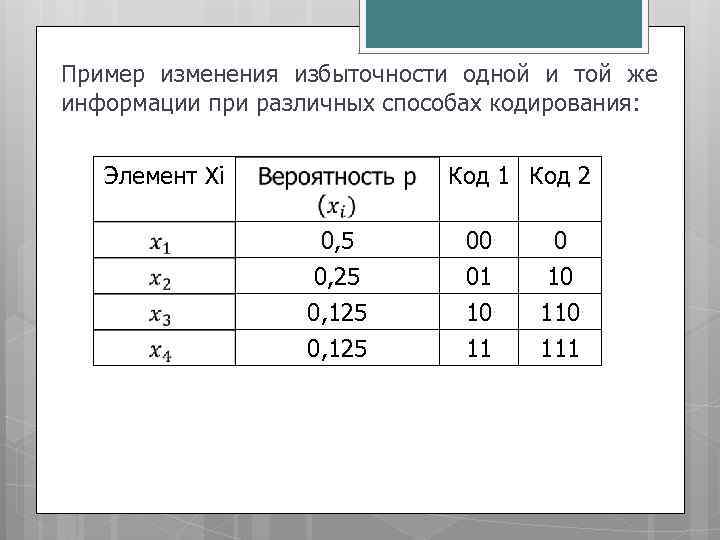Пример изменения избыточности одной и той же информации при различных способах кодирования: Элемент Хi Код 1 Код 2 0, 5 0, 25 0, 125 00 01 10 11 0 10 111

Данная теорема получила название основной теоремы эффективного кодирования. Алгоритмы построения оптимальных неравномерных кодов Для нахождения оптимальных по длине комбинаций неравномерного кода используют один из двух алгоритмов: Шеннона-Фано или Д. Хаффмана. Алгоритм Шеннона-Фано построения оптимального неравномерного кода. Алгоритм может быть применен для нахождения комбинаций неравномерного кода без разделительных знаков с любым основанием m. При построении такого кода по данному алгоритму необходимо выполнить следующую последовательность действий.

Код, построенный по данному алгоритму, это код без разделительных знаков. Это обусловлено тем, что данный алгоритм обеспечивает построение кода, у которого ни одна из комбинаций не является в целом началом другой. Первая теорема Шеннона (о кодировании при отсутствии помех): при отсутствии помех всегда возможен такой вариант кодирования, при котором среднее число знаков кода, приходящееся на один знак первичного алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов. Первичный алфавит – алфавит источника сообщения; вторичный – алфавит кодирующего устройства.

образуется единственная вспомогательная группа. На этом построение кода заканчивается. Сами комбинации кода получают, записывая в обратной последовательности вес символы, которые были приписаны набору и его вспомогательным группам. Код Хаффмана является самым экономичным из всех возможных – ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.

Длина кода выражается целым числом, следовательно, K(C, 2)=8. В компьютерных системах любому символу ставится в соответствие код из 8 двоичных разрядов (8 бит). Эта последовательность сохраняется и обрабатывается как единое целое. Кодирование символов 8 битами получило название байтовое кодирование. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении. По причине того, что вариантов сопоставления знакам первичного алфавита байтовых цепочек очень много, для совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование кодов.

Подобное согласование осуществляется в форме стандартизации кодовых таблиц. Первым стандартом был EBCDIC (расширенная двоичная кодировка десятичного кода обмена); в ПК и телекоммуникационных системах базовым стандартом являлся байтовый код ASCII.

Кодирование с неравной длительностью элементарных сигналов на примере кода Морзе В коде каждому символу соответствует некоторая последовательность точек (короткий импульс+короткая пауза) и тире (длинный импульс+короткая пауза), разделяемых паузами. Принцип кодирования заключался в том, что буквы, которые встречаются чаще, должны иметь более короткие коды, для сокращения времени передачи. Несмотря на большую избыточность, данный код был широко распространен в ситуациях, когда источником и приемником сигналов являлся человек и главным было удобство восприятия кода, а не его экономичность.

Блочное двоичное кодирование При алфавитном кодировании передаваемое сообщение представляет собой последовательность кодов отдельных знаков первичного алфавита. При блочном кодировании кодовый знак (блок) относится сразу к нескольким буквам первичного алфавита или к целому слову первичного языка. Блочное кодирование позволяет снизить избыточность почти до 0. Недостатки: • необходимо хранить огромную кодовую таблицу и постоянно к ней обращаться при кодировании и декодировании, что замедлит работу и потребует значительных ресурсов памяти;

помимо основных слов разговорный язык содержит много производных от них и в данном способе кодирования им всем нужно присвоить свои коды, что приведет к увеличению кодовой таблицы еще в несколько раз; • возникает проблема согласования (стандартизации) этих громадных таблиц; • алфавитное кодирование имеет то преимущество, что буквами можно закодировать любое слово, а при кодировании слов – можно использовать только имеющийся словарный запас. По указанным причинам блочное кодирование представляет лишь теоретический интерес, на практике же применяется кодирование алфавитное. •

Системы счисления Система счисления – это правило записи чисел с помощью заданного набора специальных знаков – цифр. Системы счисления можно объединить в следующие группы: 1. Унитарная – это система счисления, в которой для записи чисел используется только один знак – I. Следующее число получается из предыдущего добавлением новой I; их количество равно самому числу. Число представляется наиболее простым способом и, следовательно, просты операции с ним.

Непозиционная – это такая система, у которой каждая цифра сохраняет свое значение независимо от места нахождения в числе. Пример – римская система счисления, в которой базовые числа обозначены заглавными латинскими буквами: 1 -I, 5 – V, 10 – X, 50 – L, 100 – C, 500 – D, 1000 – M. Все другие числа строятся комбинациями базовых в соответствии со следующими правилами: если цифра меньшего значения стоит справа от большей, то их значения суммируются, если слева – то меньшее вычитается из большего (IV=4, XIX=19); цифры I, X, C, M могут следовать подряд не более трех раз каждая; цифры V, L, D могут использоваться в записи числа не более одного раза. 2.

Запись чисел в такой системе громоздка и неудобна, выполнение арифметических операций – затруднительно. 3. Позиционная – это система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. Количество цифр для построения чисел равно основанию системы счисления (десятичная 10 двоичная 2). Максимальная цифра на 1 меньше основания (для 10 – это 9, для 2 - 1). Главной особенностью позиционного представления чисел является то, что в нем посредством конечного набора знаков можно записать неограниченное количество различных чисел.

Двоичная система счисления – это позиционная система счисления с основанием 2. В этой системе числа записываются с помощью двух символов (0 и 1). Двоичная система счисления является частным случаем сдвоенных двоичных показательных позиционных систем счисления с обоими основаниями (a и b) равными 2.

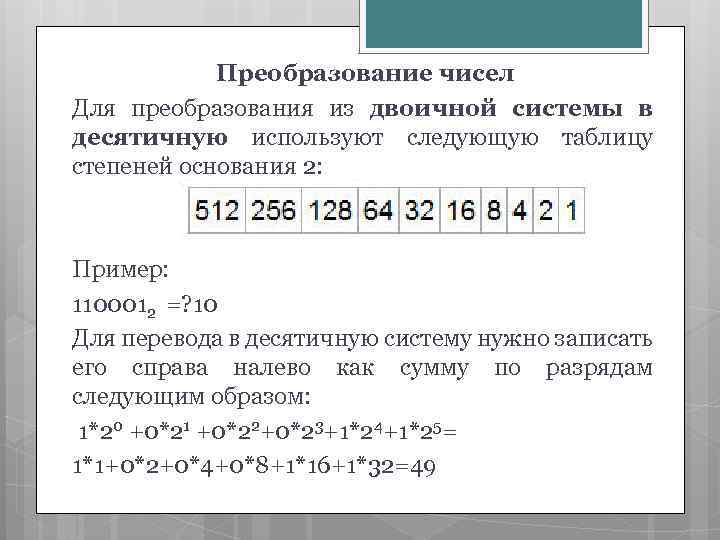Преобразование чисел Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2: Пример: 1100012 =? 10 Для перевода в десятичную систему нужно записать его справа налево как сумму по разрядам следующим образом: 1*20 +0*21 +0*22+0*23+1*24+1*25= 1*1+0*2+0*4+0*8+1*16+1*32=49

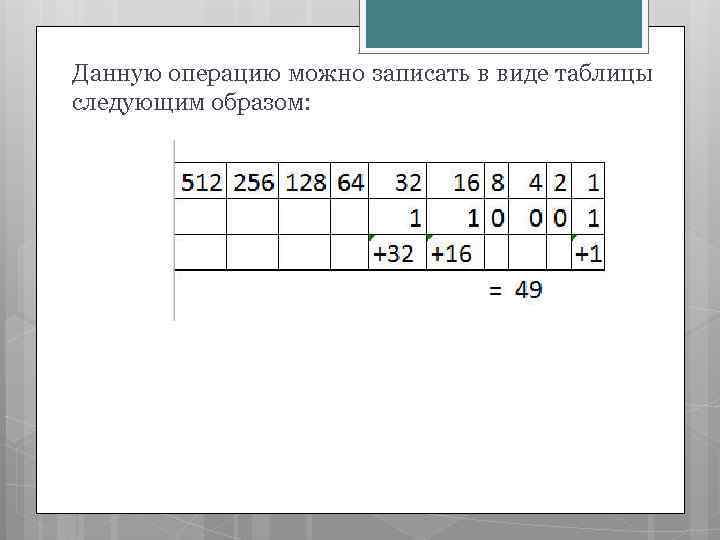Данную операцию можно записать в виде таблицы следующим образом:

Для преобразования из десятичного числа в двоичное необходимо каждое частное делить на 2 и записывать остаток в конец двоичной записи. Продолжать деление до тех пор, пока в частном не будет 0. Результат записывается справа налево, т. е. нижнее число будет самым левым и т. д. 1810 = 100102

Преобразование дробных десятичных чисел в двоичные Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму: Вначале переводится целая часть десятичной дроби в двоичную систему счисления; Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления; В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага. Пример: Требуется перевести дробное десятичное число 206, 116 в дробное двоичное число. Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

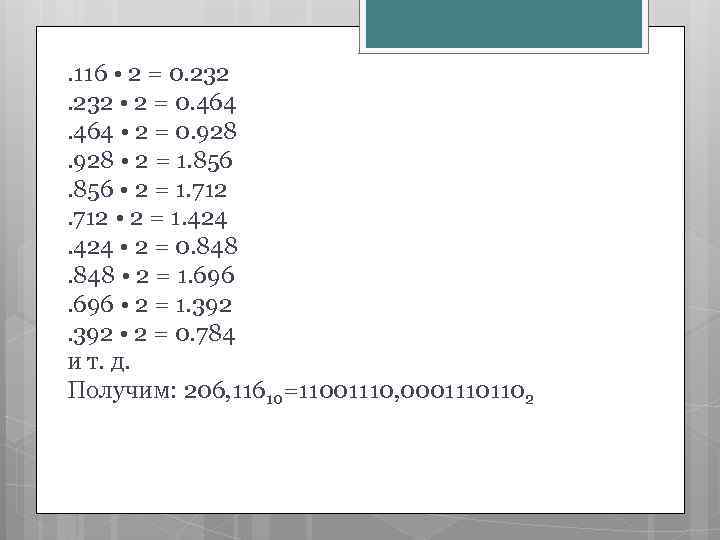. 116 • 2 = 0. 232 • 2 = 0. 464 • 2 = 0. 928 • 2 = 1. 856 • 2 = 1. 712 • 2 = 1. 424 • 2 = 0. 848 • 2 = 1. 696 • 2 = 1. 392 • 2 = 0. 784 и т. д. Получим: 206, 11610=11001110, 00011101102

Операции над двоичными числами Сложение, вычитание, умножение двоичных чисел производится по следующим правилам: 0+0=0 0+1=1 1+0=1 1+1=10 0 -0=0 1 -0=1 1 -1=0 10 -1=1 0*0=0 0*1=0 1*0=0 1*1=1

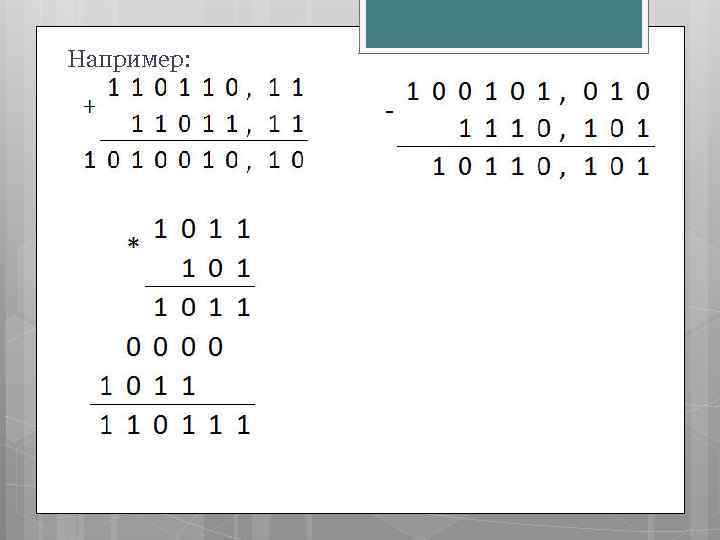Например:

Восьмеричная система счисления - позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры 0 до 7. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Восьмеричная система часто использовалась в областях, связанных с цифровыми устройствами, но в настоящее время почти полностью вытеснена шестнадцатеричной.

Для перевода чисел из десятичной системы счисления в восьмеричную используют тот же "алгоритм замещения", что и при переводе из десятичной системы счисления в двоичную, только в качестве делителя используют 8. Для перевода восьмеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания восьмеричной системы счисления на соответствующие цифры в разрядах восьмеричного числа: 23578=(2· 83)+(3· 82)+(5· 81)+(7· 80) = 2· 512 + 3· 64 + 5· 8 + 7· 1 = 126310

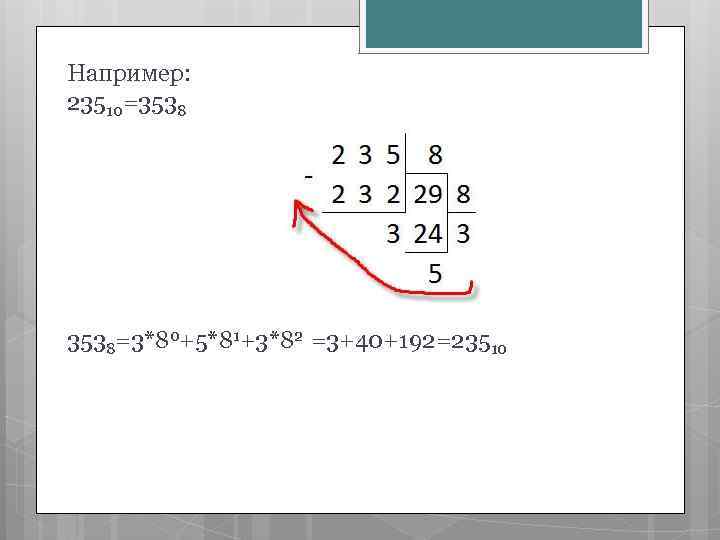Например: 23510=3538=3*80+5*81+3*82 =3+40+192=23510

Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например: 25418 = 010 101 100 0012 Таблица перевода восьмеричных чисел в двоичные: 08 = 0002 18 = 0012 28 = 0102 38 = 0112 48 = 1002 58 = 1012 68 = 1102 78 = 1112

Для перевода двоичного числа в восьмеричное необходимо разбить это двоичное число на триады, начиная с младшего разряда, если старшая триада не заполнена до конца, следует дописать в ее старшие разряды нули. После этого необходимо заменить двоичные триады, начиная с младшей, на числа, равные им в восьмеричной системе. Например: 1010011102=5168 10011012=1158

Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16. В качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8 -битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр. Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде (#cf 12 db).

Перевод чисел из шестнадцатеричной системы в десятичную Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа. Например: 5 А 316 = ? 10 5*162+10*161+3*160=1280+160+3=144310

Перевод чисел из десятичной системы в шестнадцатеричную Для перевода чисел из десятичной системы счисления в шестнадцатеричную используют тот же "алгоритм замещения", что и при переводе из десятичной системы счисления в двоичную и восьмеричную, только в качестве делителя используют 16, основание шестнадцатеричной системы счисления. Например: 3276710 = ? 16 3276710 = 7 FFF 16

Перевод чисел из двоичной системы в шестнадцатеричную Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Например: 0101101000112 = 0101 1010 0011 = 5 A 316

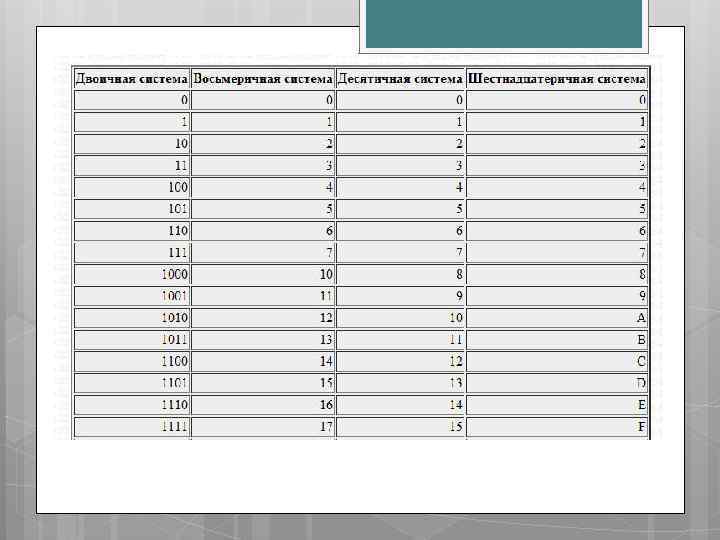
Кодирование числовой информации Помехоустойчивое кодирование применяется для обнаружения и исправления ошибок, которые могут возникнуть в дискретном сигнале при его передаче по каналам связи. В качестве базового кода, подвергающегося помехоустойчивому кодированию, используется двоичный код постоянной длины. Такой исходный код называется первичным. Количество разрядов n в кодовой комбинации называется значностью кода или длиной. Количество единиц в коде называется весом кодовой комбинации.

Например: кодовая комбинация 1100101 характеризуется значностью n=7 и весом V=4. Степень отличия кодовых комбинаций характеризуется кодовым расстоянием d (кодовое расстояние по Хеммингу). Для двух двоичных слов кодовое расстояние по Хеммингу есть число разрядов, в которых разнятся эти слова. Например, для слов 11011 и 10110 кодовое расстояние d = 3, так как эти слова различаются в трех разрядах (первом, третьем и четвертом). С ошибкой связано понятие ее кратности q – число искаженных разрядов. При этом « 1 0» и « 0 1» . Если произошла ошибка в одном разряде, она называется однократной, иначе – двукратной, трехкратной и т. д.

Для указания разрядов в кодовой комбинации, где произошли ошибки, используется понятие вектор ошибки e. Вектор ошибки n-разрядного кода – это n-разрядная комбинация, где единицы указывают положение разрядов искаженных символов. Например: е = 0101, то искажены символы в первом и третьем разрядах. Вес вектора ошибки характеризует кратность ошибки me. Помехоустойчивые коды характеризуются корректирующей способностью, которая определяется вероятностью обнаружения или исправления ошибки. Корректирующая способность кода основана на понятиях разрешенных и запрещенных кодовых комбинаций. Помехоустойчивость кодов обеспечивается за счет

введения избыточности, т. е. из общего количества n символов комбинации для передачи используется только часть – m символов (m

Если после приема сигнала установлено, что комбинация относится к группе разрешенных, то считается, что сигнал пришел без искажения. В противном случае сигнал считается искаженным. От эффективности метода кодирования, а именно от алгоритма кодирования и его реализации, зависит качество цифровой передачи данных.

Кодирование с проверкой на четность Для данного метода кодирования выполняют суммирование цифр по модулю 2 (остаток от деления на 2), входящих в контролируемый код. Вместе с передаваемым кодом передается один контрольный разряд. Его значение (1 или 0) выбирается с условием, чтобы сумма цифр в передаваемом коде была по модулю 2 равна 0 – для случая четности и 1 – для случая нечетности. При таком кодировании допускается, что может возникнуть только одна ошибка. Признаком отсутствия искажений в процессе приема-передачи является равенство контрольного числа нулю (сумма по модулю 2 исходной комбинации и контрольного разряда).

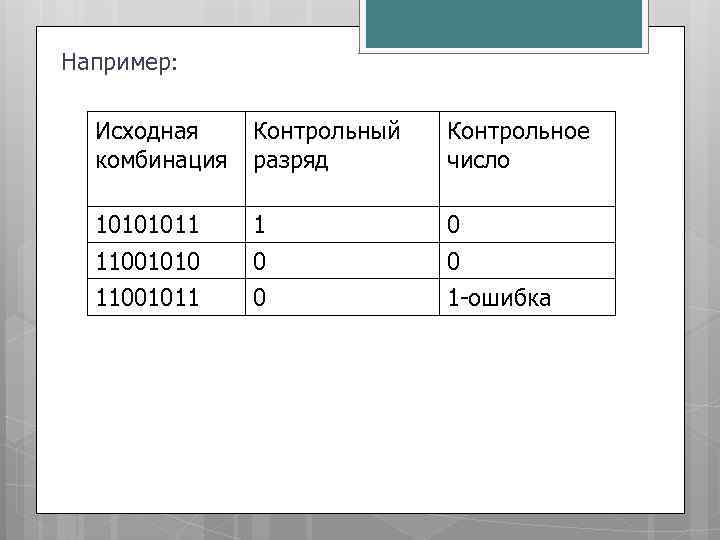Например: Исходная комбинация Контрольный разряд Контрольное число 10101011 1 0 11001010 0 0 11001011 0 1 -ошибка

Кодирование с удвоением элемента Данный метод характеризуется наличием дополнительного символа для каждого информационного символа передаваемого кода. Информация « 1» представляется как 10, а « 0» - как 01 (например: исходная комбинация 1011 преобразуется в 10011010). Показателем искажения являются сочетания типа 00 и 11 в парных элементах. Код не исправляет ошибки, приводящие к двукратным противоположным изменениям разрядов в парных элементах. Помехоустойчивость данного кода выше, чем кода с проверкой на четность, но существенно возрастает избыточность кода.

Инверсное кодирование В основе метода лежит повторение кодовой комбинации. Если исходная комбинация содержит четное число единиц, то повторная комбинация в точности повторяет исходную. Иначе повторение происходит в инверсном виде. Например, комбинация 01010 в инверсном коде представляется как 01010, а комбинация 11010 – как 1101000101. Проверка производится суммированием единиц основной комбинации. Если их число четно, то элементы второй части принимаются в том же виде, после чего обе части комбинации сравниваются поэлементно – первый элемент первой части с первым элементом второй части. При несовпадении хотя бы одного элемента принятая комбинация считается неверной.

Инверсный код позволяет обнаружить практически все ошибки приема-передачи. Не обнаруживается лишь одновременное искажение парных элементов в обеих частях кодовой комбинации.

Код проверки по методу Хэмминга Исправляет одиночные ошибки. Содержит комбинация m информационные и k = n-m –избыточных символов. Избыточная часть кода строится так, чтобы при декодировании можно было установить не только наличие ошибки, но и ее положение. Это достигается путем многократной проверки принятой комбинации на четность. Количество проверок равно значению избыточных символов k. При каждой проверке охватывается часть информационных символов и один избыточный, при этом получают один контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение « 0» , если нечетное – « 1» . В результате всех проверок получается k-разрядное двоичное число,

Линейные коды. Циклические коды Значения проверочных символов линейных кодов определяются в результате проведения линейных операций над определенными информационными символами. Для случая двоичных кодов каждый проверочный символ выбирают таким образом, чтобы его сумма с определенными информационными символами была равна 0. Символ проверочной позиции имеет значение 1, если число единиц информационных разрядов, входящих в данное проверочное равенство, нечетно, и 0, если оно четно. Число проверочных равенств (а следовательно, и число проверочных символов) и номера конкретных информационных разрядов, входящих в каждое из равенств, определяется тем, какие и сколько ошибок должен исправлять или обнаруживать данный код.

Проверочные символы могут располагаться на любом месте кодовой комбинации. При декодировании определяется справедливость проверочных равенств. В случае двоичных кодов такое определение сводится к проверкам на четность числа единиц среди символов, входящих в каждое из равенств (включая проверочные). Совокупность проверок дает информацию о том, имеется ли ошибка, а в случае необходимости и о том, на каких позициях символы искажены. Любой двоичный линейный код является групповым, так как совокупность входящих в него кодовых комбинаций образует группу

Циклические коды. Основное свойство циклических кодов: если некоторая комбинация принадлежит циклическому коду, то комбинация, полученная циклическим сдвигом (перемещение элементов кодовой комбинации справа налево без нарушения порядка их следования) исходной комбинации, также принадлежит данному коду: (a 1, a 2, …, an)→(an, a 1, a 2, …, an-1) Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином (многочлен, состоящий из величин, отделенных знаками + или -), называемый производящим. Данное свойство используется при построении кодов кодирующих и декодирующих устройств, а также при обнаружении и

исправлении ошибок. Циклические коды относятся к систематическим блочным (n, k) помехоустойчивым кодам, в которых k первых разрядов представляют собой комбинацию первичного кода, а последующие (n -k) разрядов являются проверочными. В основе построения циклических кодов лежит операция деления передаваемой кодовой комбинации на порождающий неприводимый полином степени r. Остаток от деления используется при формировании проверочных разрядов. При этом операции деления предшествует операция умножения, осуществляющая сдвиг влево k-разрядной информационной кодовой комбинации на r разрядов. При декодировании принятой n-разрядной комбинации опять производится деление на порождающий полином.

Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на порождающий полином. Если синдром равен нулю, то считается, что ошибок нет. В противном случае с помощью полученного синдрома можно определить номер разряда принятой комбинации, в котором произошла ошибка и исправить ее.

Способы передачи данных в линиях связи В компьютерных линиях связи используются два способа передачи: последовательный, когда биты передаются поочередно, начиная с младшего; параллельный, когда передаются одновременно все биты машинного слова.

Последовательная передача данных Для передачи информации на большие расстояния, например, при объединении компьютеров в сети, используется последовательный способ передачи. Возможны два режима последовательной передачи: синхронный и асинхронный. При синхронной передаче каждый передаваемый бит сопровождается импульсом синхронизации, информирующим приемник о наличии в линии информационного бита. Синхронизирующие импульсы управляют приемом информации. Следовательно, между передатчиком и приемником должны быть протянуты минимум три провода: один – для передачи данных, второй – для передачи синхроимпульсов, третий – общий заземленный.

Синхронная последовательная передача начинается с пересылки в приемник одного или двух символов синхронизации. Получив такой символ (символы), приемник начинает прием данных и их преобразование в параллельный формат. При такой организации синхронной последовательной передачи она целесообразна лишь для пересылки массивов слов, а не отдельных символов. Это обстоятельство, а также необходимость использования для обмена сравнительно дорогих линий связи привели к тому, что синхронный способ передачи данных связи не получил широкого распространения.

Асинхронный способ передачи не требует синхронизации действий приемника и передатчика; по этой причине для связи достаточно линии из двух проводников. Возможно использование неспециализированных компьютерных линий (например, телефонных). При этом источник и приемник информации должны быть согласованы по формату и скорости передачи. Передача производится машинными словами (информационными битами), дополненными несколькими служебными.

Процедура асинхронной последовательной передачи данных: Стандартный формат асинхронной последовательной передачи данных, используемый в ЭВМ и ВУ, содержит n пересылаемых бит информации (при пересылке символов n равно 7 или 8 битам) и 3 -4 дополнительных бита: стартовый бит, бит контроля четности (или нечетности) и 1 или 2 стоповых бита. Бит четности (или нечетности) может отсутствовать. Когда передатчик бездействует (данные не посылаются на линию), на линии сохраняется уровень сигнала, соответствующий логической 1, например +5 В:

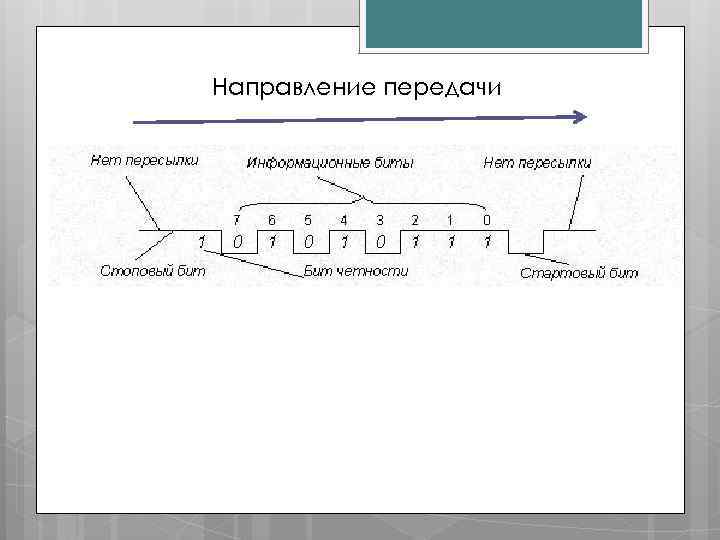Направление передачи

Передатчик может начать пересылку символа в любой момент времени посредством генерирования стартового бита, т. е. перевода линии в состояние логического 0 на время продолжительности элементарного сигнала τ0 – по нему приемник узнает, что передача началась. Затем происходит передача битов символа, начиная с младшего значащего бита, за которым следует дополнительный бит контроля по четности или нечетности. Далее с помощью стопового бита линия переводится в состояние логической 1. Стоповых бит может быть 1 или 2. Состояние логической 1 должно поддерживаться в течение промежутка времени, равного 1 или 2 временам передачи бита.

Промежуток времени от начала стартового бита до конца стопового бита (стоповых бит) называется кадром. Новый стартовый бит может быть послан в любой момент времени после окончания стопового бита, поэтому передача и называется асинхронной. Данная схема передачи требует предварительного согласования передатчика и приемника по продолжительности элементарного сигнала. Кроме того, для обеспечения максимальной защищенности сигнала от искажений приемник настраивается на считывание бита в середине его длительности. Преимуществом данного способа передачи является то, что в нем нет ограничений на дальность передачи.

Параллельная передача данных является по своей организации наиболее простым способом обмена. Для одновременной передачи нескольких сигналов требуется линия связи, количество проводников в которой совпадает с числом передаваемых сигналов. Такая линия связи называется шиной. Количество проводников определяет ширину или разрядность шины.

линия параллельной передачи, связывающая регистр АЛУ и ячейку памяти компьютера Шина обеспечивает наиболее быстрый способ передачи информации, поскольку за два такта синхрогенератора компьютера передается целое машинное слово.

Параллельный способ передачи используется во внутренних линиях связи компьютера (на материнской плате; при обмене информацией с устройствами внешней памяти – магнитными дисками, CD-ROM), а также для связи с внешними устройствами, подключаемыми к параллельному порту компьютера (LPT – порту): принтером, плоттером (графопостроителем) и др.

К недостаткам параллельного способа передачи следует отнести, во-первых, то, что им невозможна передача на большие расстояния, поскольку между параллельными проводниками имеется электроемкость, увеличивающаяся с их длиной, существование которой приводит к тому, что при протекании импульса по какому-либо одному проводнику возникают наводки в других. Во-вторых, данный способ требует многожильных специальных проводов для связи, что существенно повышает стоимость линии.

Данные Классификация. Представление. Иерархические структуры Данные – это сведения, характеризующие какую-то систему, явление, процесс или объект, представленные в определенной форме и предназначенные для дальнейшего использования. В компьютерных системах любая информация, представленная в доступной для компьютера форме, считается данными. Классификационные признаки данных: Тип данных. Он определяет: Набор их допустимых значений; Правила их обработки;

Порядок размещения в ОЗУ и ВЗУ при хранении; Порядок доступа к ним (обращение и извлечение с места хранения). Деление данных на элементарные (одиночные, простые) и структурированные (сложные). К элементарным данным относят символы, числа и логические данные. Особенностью одиночные данных является то, что каждое из них имеет одно значение и собственное имя (идентификатор). По возможности изменения значений данных в ходе общей обработки их подразделяют на переменные и постоянные. Переменные могут изменять свое значение по ходу исполнения программы, а константы – нет.

В зависимости от того, на каком этапе обработки данные используются, они подразделяются на: Исходные (входные) – необходимые для исполнения программы и вносимые в нее до или в процессе работы; Промежуточные – формируются в ходе исполнения программы и пользователю недоступны; Выходные – результат работы программы. Представление данных является важным фактором, обеспечивающим компактный способ записи информации при хранении и быстрый доступ к нужным данным при использовании. Выделяют три уровня представления данных:

1. 2. 3. Концептуальный – на данном уровне определяется общая структура информационного массива – модель данных; Логический – определяет способы представления элементарных данных, их перечень при объединении в структуру, а также характер связей между ними; Физический – определяет форматы размещения созданной логической структуры данных на внешних носителях. Классификация структур данных Классификационные признаки структур данных:

1. 2. По порядку данных структуры делятся на упорядоченные и неупорядоченные. В упорядоченных элементы размещаются по порядку в соответствии со значением некоторого признака, например порядкового номера элемента. Порядковый номер – внешний признак, который присваивается элементу независимо от его значения. В неупорядоченных структурах (множествах) не определен порядок элементов, единственное, что можно установить для данных – это их принадлежность выбранному множеству. Однородность. К однородным относят структуры, содержащие данные только одного типа (массивы, стеки). Неоднородные – объединяют данные разных типов (записи).

Характер отношений: линейные структуры – все элементы равноправны; нелинейные структуры – между элементами существуют отношения подчиненности или они м. б. связаны логическими условиями (деревья, графы). Массив – упорядоченная линейная совокупность однородных данных. Стек – упорядоченная, линейная, неоднородная структура. Реализуется как специальная область ОЗУ или самостоятельный блок памяти. Вход в стек возможен только через первую ячейку памяти (вершину стека) и извлекаться первой будет та информация, которая была занесена последней. Дерево (иерархия) – нелинейная структура, в которой элемент каждого уровня (кроме первого) входит в один элемент следующего (более высокого) уровня. 3.

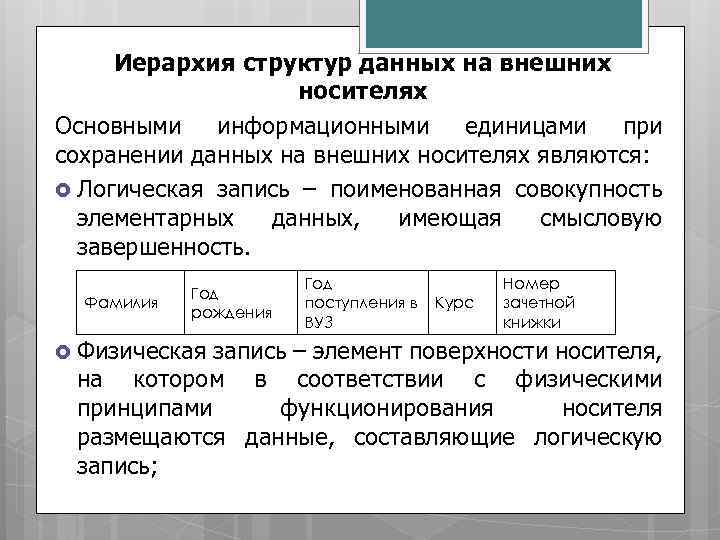Иерархия структур данных на внешних носителях Основными информационными единицами при сохранении данных на внешних носителях являются: Логическая запись – поименованная совокупность элементарных данных, имеющая смысловую завершенность. Фамилия Год рождения Год поступления в ВУЗ Курс Номер зачетной книжки Физическая запись – элемент поверхности носителя, на котором в соответствии с физическими принципами функционирования носителя размещаются данные, составляющие логическую запись;

Файл – совокупность физических записей, рассматриваемая как единое целое и имеющая описание в системе хранения информации; Каталог – место размещения файлов, определенных каким-либо признаком. FTA – таблица размещения файлов, в которую заносятся имена и атрибуты файлов, а также номер кластера, с которого начинается размещение файла.