Математические задачи в ЭЭ Основы расчета.pptx
- Количество слайдов: 33
 Основы расчета установившихся режимов электроэнергетических систем Математические задачи в ЭЭ
Основы расчета установившихся режимов электроэнергетических систем Математические задачи в ЭЭ
 1. Техническая постановка задачи 1. 2. 3. 4. Определяется особенностями ЭЭС. Включает в себя большое количество элементов. Элементы ЭЭС вырабатывают, преобразуют, распределяют, потребляют эл. энергию. Элементы ЭЭС образуют сложнозамкнутую разветвленную структуру.
1. Техническая постановка задачи 1. 2. 3. 4. Определяется особенностями ЭЭС. Включает в себя большое количество элементов. Элементы ЭЭС вырабатывают, преобразуют, распределяют, потребляют эл. энергию. Элементы ЭЭС образуют сложнозамкнутую разветвленную структуру.
 Факторы, обуславливающие функционирование ЭЭС 1. 2. 3. Непрерывность процесса производства, распределения, потребления ЭЭ. Динамизм ЭЭС ( постоянное изменение техологических параметров). Сложность структурных связей. Режимом работы ЭЭС называется состояние системы в любой момент времени или на некотором интервале времени. Под установившимся режимом понимается такое состоянии ЭЭС, когда параметры системы на рассматриваемом интервале времени сохраняются неизменными или изменяются достаточно медленно.
Факторы, обуславливающие функционирование ЭЭС 1. 2. 3. Непрерывность процесса производства, распределения, потребления ЭЭ. Динамизм ЭЭС ( постоянное изменение техологических параметров). Сложность структурных связей. Режимом работы ЭЭС называется состояние системы в любой момент времени или на некотором интервале времени. Под установившимся режимом понимается такое состоянии ЭЭС, когда параметры системы на рассматриваемом интервале времени сохраняются неизменными или изменяются достаточно медленно.
 Задача расчета установившихся режимов ЭЭС - 1. 2. 3. 4. 5. определение совокупности параметров, характеризующих работу системы: напряжений в различных точках системы, токов в ее элементах, потоков энергии и потерь мощности и т. д. Этапы расчета: Предварительное преобразование и переход к расчетной схеме ЭЭС. Формирование уравнений состояния по известным исходным данным. Выбор метода расчета, составление алгоритма и программы. Проведение расчета установившегося режима. Анализ точности полученных результатов.
Задача расчета установившихся режимов ЭЭС - 1. 2. 3. 4. 5. определение совокупности параметров, характеризующих работу системы: напряжений в различных точках системы, токов в ее элементах, потоков энергии и потерь мощности и т. д. Этапы расчета: Предварительное преобразование и переход к расчетной схеме ЭЭС. Формирование уравнений состояния по известным исходным данным. Выбор метода расчета, составление алгоритма и программы. Проведение расчета установившегося режима. Анализ точности полученных результатов.
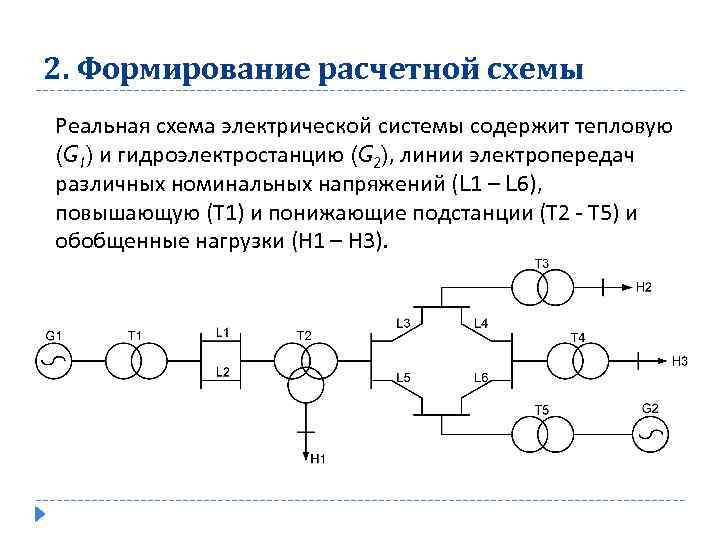 2. Формирование расчетной схемы Реальная схема электрической системы содержит тепловую (G 1) и гидроэлектростанцию (G 2), линии электропередач различных номинальных напряжений (L 1 – L 6), повышающую (Т 1) и понижающие подстанции (Т 2 - Т 5) и обобщенные нагрузки (Н 1 – Н 3).
2. Формирование расчетной схемы Реальная схема электрической системы содержит тепловую (G 1) и гидроэлектростанцию (G 2), линии электропередач различных номинальных напряжений (L 1 – L 6), повышающую (Т 1) и понижающие подстанции (Т 2 - Т 5) и обобщенные нагрузки (Н 1 – Н 3).
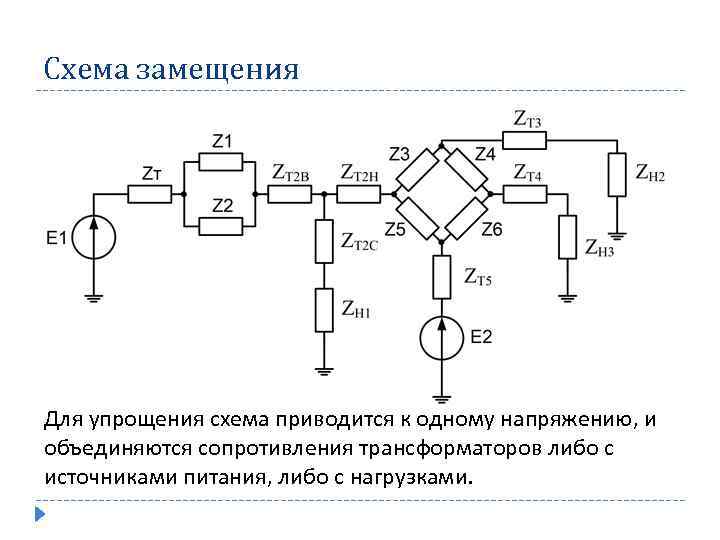 Схема замещения Для упрощения схема приводится к одному напряжению, и объединяются сопротивления трансформаторов либо с источниками питания, либо с нагрузками.
Схема замещения Для упрощения схема приводится к одному напряжению, и объединяются сопротивления трансформаторов либо с источниками питания, либо с нагрузками.
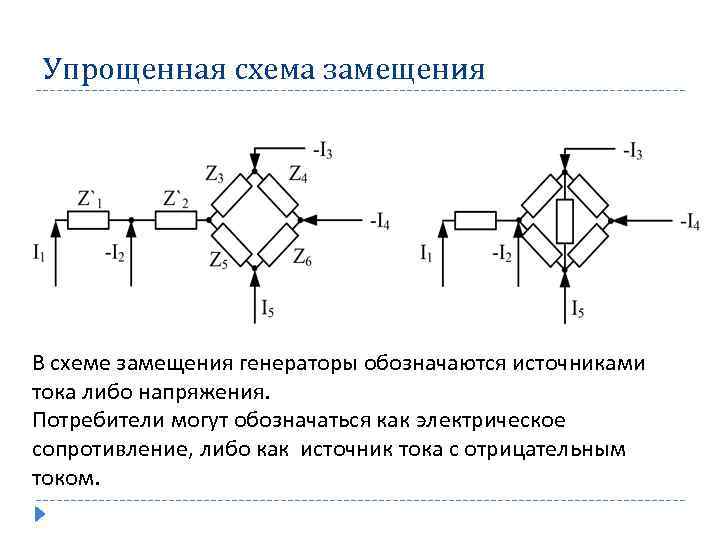 Упрощенная схема замещения В схеме замещения генераторы обозначаются источниками тока либо напряжения. Потребители могут обозначаться как электрическое сопротивление, либо как источник тока с отрицательным током.
Упрощенная схема замещения В схеме замещения генераторы обозначаются источниками тока либо напряжения. Потребители могут обозначаться как электрическое сопротивление, либо как источник тока с отрицательным током.
 Составление графа на основе метода контурных токов
Составление графа на основе метода контурных токов
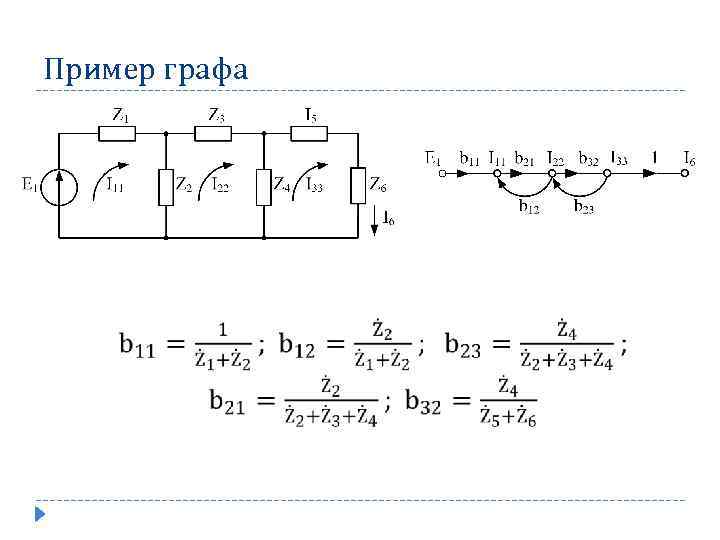 Пример графа
Пример графа
 Составление графов на основе метода узловых потенциалов
Составление графов на основе метода узловых потенциалов
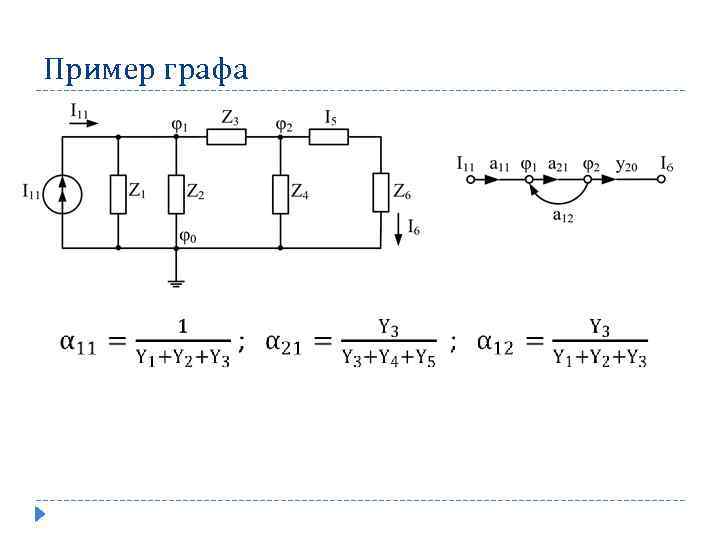 Пример графа
Пример графа
 3. Матричная форма представления основных законов электротехники
3. Матричная форма представления основных законов электротехники
 Матричная форма уравнений состояния ЭЭС Матричное уравнение состояния ЭЭС - система уравнений, описывающая режим работы ЭЭС. Виды матричных уравнений состояния: Обобщенное уравнение состояния. Уравнение узловых напряжений. Уравнение контурных токов.
Матричная форма уравнений состояния ЭЭС Матричное уравнение состояния ЭЭС - система уравнений, описывающая режим работы ЭЭС. Виды матричных уравнений состояния: Обобщенное уравнение состояния. Уравнение узловых напряжений. Уравнение контурных токов.
 1) Обобщенное уравнение состояния
1) Обобщенное уравнение состояния
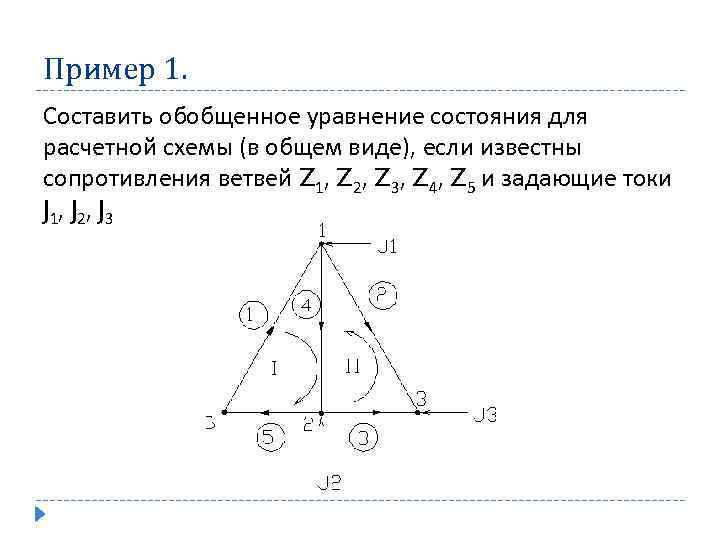 Пример 1. Составить обобщенное уравнение состояния для расчетной схемы (в общем виде), если известны сопротивления ветвей Z 1, Z 2, Z 3, Z 4, Z 5 и задающие токи J 1, J 2, J 3
Пример 1. Составить обобщенное уравнение состояния для расчетной схемы (в общем виде), если известны сопротивления ветвей Z 1, Z 2, Z 3, Z 4, Z 5 и задающие токи J 1, J 2, J 3
 Пример 1. Составим матрицы инциденций M и N
Пример 1. Составим матрицы инциденций M и N
 Пример 1. Составим матрицы задающих параметров
Пример 1. Составим матрицы задающих параметров
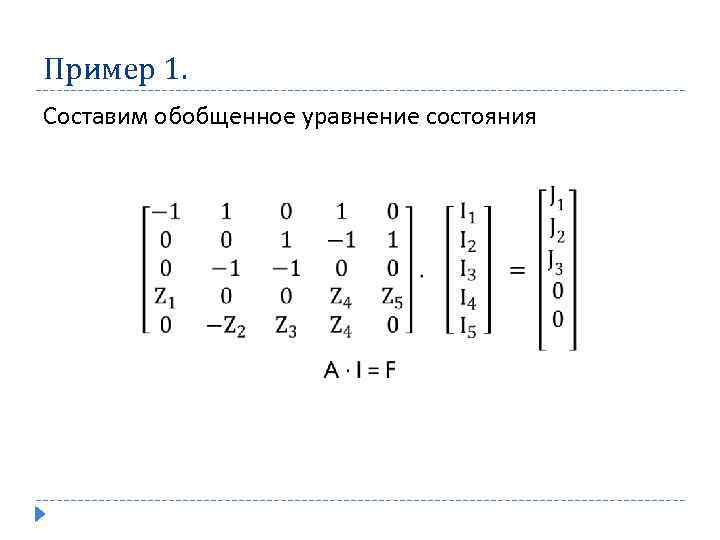 Пример 1. Составим обобщенное уравнение состояния
Пример 1. Составим обобщенное уравнение состояния
 Пример 1. Рассчитаем установившийся режим работы ЭЭС 1) Определим токи в ветвях схемы I = A-1 F 2) Рассчитаем падения напряжений в ветвях схемы на основе закона Ома UB = ZBI - EB 3) Определим узловые напряжения по уравнению связи параметров UΔ = Mt-1 UB 4) На основе полученных данных рассчитаем остальные параметры режима: потоки мощности P, Q; потери ΔР, ΔQ и т. д.
Пример 1. Рассчитаем установившийся режим работы ЭЭС 1) Определим токи в ветвях схемы I = A-1 F 2) Рассчитаем падения напряжений в ветвях схемы на основе закона Ома UB = ZBI - EB 3) Определим узловые напряжения по уравнению связи параметров UΔ = Mt-1 UB 4) На основе полученных данных рассчитаем остальные параметры режима: потоки мощности P, Q; потери ΔР, ΔQ и т. д.
 2) Матричная форма представления уравнения узловых напряжений
2) Матричная форма представления уравнения узловых напряжений
 Этапы расчета по методу узловых напряжений
Этапы расчета по методу узловых напряжений
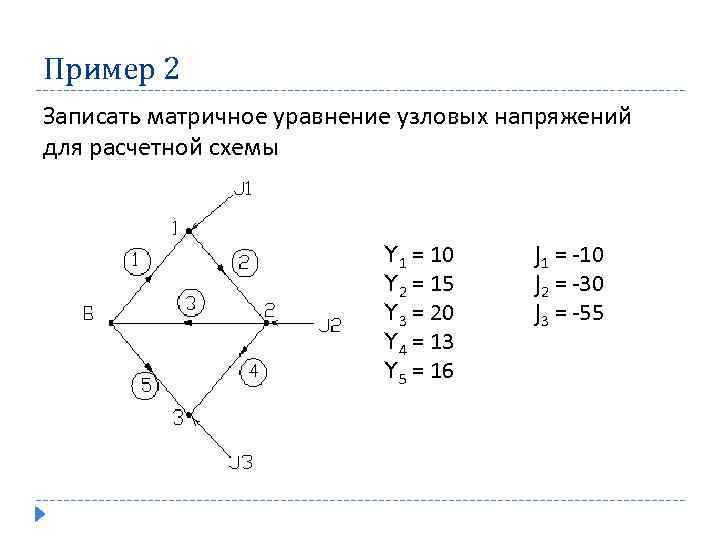 Пример 2 Записать матричное уравнение узловых напряжений для расчетной схемы Y 1 = 10 J 1 = -10 Y 2 = 15 J 2 = -30 Y 3 = 20 J 3 = -55 Y 4 = 13 Y 5 = 16
Пример 2 Записать матричное уравнение узловых напряжений для расчетной схемы Y 1 = 10 J 1 = -10 Y 2 = 15 J 2 = -30 Y 3 = 20 J 3 = -55 Y 4 = 13 Y 5 = 16
 Пример 2 Составим матрицу инциденций M, найдем транспонированную матрицу М
Пример 2 Составим матрицу инциденций M, найдем транспонированную матрицу М
 Пример 2
Пример 2
 Пример 2
Пример 2
 3) Матричная форма представления уравнений контурных токов
3) Матричная форма представления уравнений контурных токов
 Матричная форма представления уравнений контурных токов при наличии задающих токов
Матричная форма представления уравнений контурных токов при наличии задающих токов
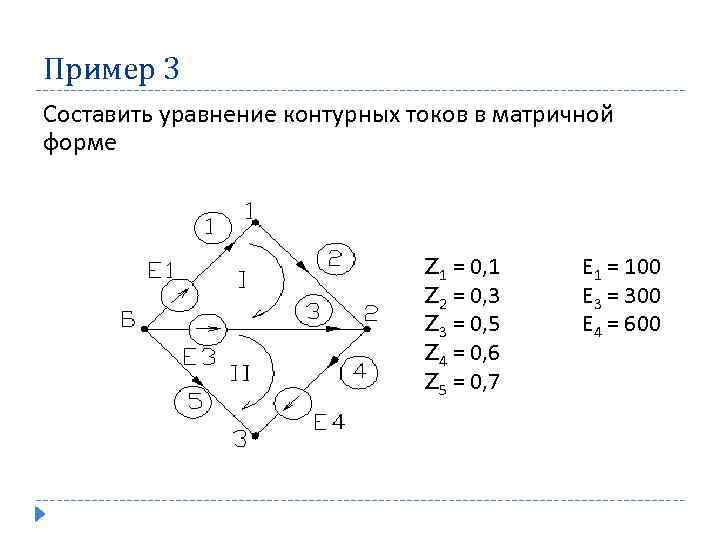 Пример 3 Составить уравнение контурных токов в матричной форме Z 1 = 0, 1 Е 1 = 100 Z 2 = 0, 3 Е 3 = 300 Z 3 = 0, 5 Е 4 = 600 Z 4 = 0, 6 Z 5 = 0, 7
Пример 3 Составить уравнение контурных токов в матричной форме Z 1 = 0, 1 Е 1 = 100 Z 2 = 0, 3 Е 3 = 300 Z 3 = 0, 5 Е 4 = 600 Z 4 = 0, 6 Z 5 = 0, 7

 Пример 3
Пример 3
 Пример 3
Пример 3
 Пример 3
Пример 3
 Литература: 1. 2. 3. 4. 5. Электрические системы. Математические задачи электроэнергетики. – М. : Высшая школа, 1981. Жуков Л. А. , Стратан И. П. Установившиеся режимы сложных электрических сетей и систем. Методы расчетов. – М. : Энергия, 1979. Электрические системы. Режимы работы электрических систем и сетей / Под ред. В. А. Веникова. – М. : Высш. шк. , 1975 Касаткин А. С. , Немцов М. В. Электротехника: учеб. пособие. – М. : Энергоатомиздат, 1983. Лыкин А. В. Электрические системы и сети: учеб. пособие. – М. : Университетская книга; Логос, 2006.
Литература: 1. 2. 3. 4. 5. Электрические системы. Математические задачи электроэнергетики. – М. : Высшая школа, 1981. Жуков Л. А. , Стратан И. П. Установившиеся режимы сложных электрических сетей и систем. Методы расчетов. – М. : Энергия, 1979. Электрические системы. Режимы работы электрических систем и сетей / Под ред. В. А. Веникова. – М. : Высш. шк. , 1975 Касаткин А. С. , Немцов М. В. Электротехника: учеб. пособие. – М. : Энергоатомиздат, 1983. Лыкин А. В. Электрические системы и сети: учеб. пособие. – М. : Университетская книга; Логос, 2006.


