ОСНОВЫ РАБОТЫ В MS EXCEL РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО

ОСНОВЫ РАБОТЫ В MS EXCEL. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА БАЗЕ MS Excel Лабораторная работа № 4 1

Цель работы • Получить и закрепить навыки работы с числовыми данными и диаграммами в табличном процессоре MS Excel. • Освоить методику решения линейных задач оптимизации с помощью средств MS Excel. 2

Задания 1. Создать в MS Excel книгу ведомостей и консолидации заработной платы небольшой фирмы за первый квартал некоторого года. 2. Найти решение с помощью MS Excel производственной задачи. 3

Краткая теория • Для вычисления значений в ячейках используются формулы, которые начинаются со значка «=» . • Ячейки с необходимыми значениями адресуются в формулах буквой (буквами или номером) столбца и номером строки. Пример: A 20, BC 11. • Можно использовать относительную адресацию. • В этом случае необходимо включить стиль ссылок R 1 C 1. Данная настройка осуществляется через меню Сервис -> Параметры, вкладка «Общие» . • Пример: – Формула вписывается в ячейку с адресом R 15 C 3. Необходимо использовать ячейку, которая отступает по горизонтали на две позиции влево, а по вертикали на три позиции вниз. В этом случае такая ячейка адресуется как R[-2]C[3]. 4

Краткая теория • • Если значения в колонке или в строке вычисляется по одной и той же формуле, которая на соответствующие ячейки соседних колонок или строк, то достаточно эту формулу ввести один раз и распространить на оставшиеся ячейки либо через буфер обмена или с помощью мыши, «потянув» нижний правый угол ячейки в нужную сторону. Если для расчет смежных ячеек необходимо провести расчет с использование значения одной и той же ячейки, то на нее лучше ссылаться с помощью абсолютного адреса (например, $A$20 или R 29 C 1) или этой ячейке присвоить уникальное имя. 5

• Когда в расчете требуется использовать значения, хранящиеся в ячейках, которые расположены в других листах книги, то можно использовать имена листов и «!» . – Пример: СУММ(‘Лист1’!A 1: A 20). • Если требуется консолидировать данные из нескольких смежных листов (листы, которые идут подряд), то в формуле указывается диапазон листов через двоеточие. – Пример: СУММ(‘Январь’: ’Декабрь’!A 20). 6

Задание 1 • Создать в MS Excel книгу ведомостей и консолидации заработной платы небольшой фирмы за первый квартал некоторого года. • Книга должна содержать пять листов. • Первый лист под названием «Оклады и проценты» должен содержать справочные сведения (процент надбавки от оклада и процент компенсации от оклада, ставка подоходного налога, ставка удержания в ПФР и оклады сотрудников). 7

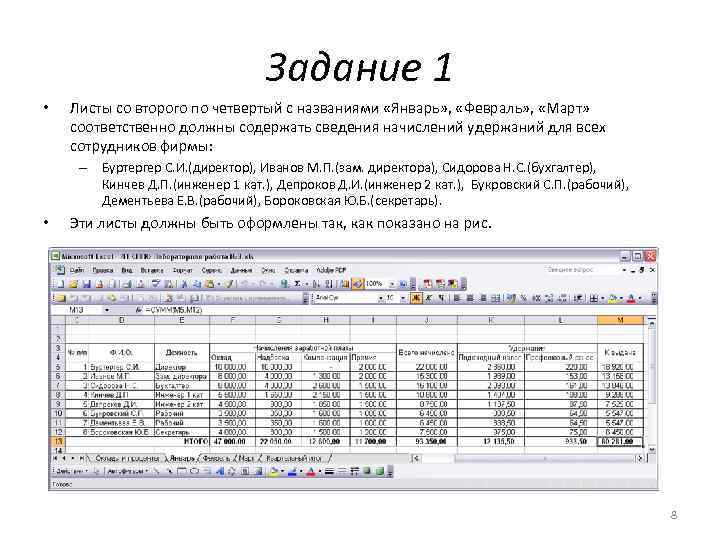
Задание 1 • Листы со второго по четвертый с названиями «Январь» , «Февраль» , «Март» соответственно должны содержать сведения начислений удержаний для всех сотрудников фирмы: – Буртергер С. И. (директор), Иванов М. П. (зам. директора), Сидорова Н. С. (бухгалтер), Кинчев Д. П. (инженер 1 кат. ), Депроков Д. И. (инженер 2 кат. ), Букровский С. П. (рабочий), Дементьева Е. В. (рабочий), Бороковская Ю. Б. (секретарь). • Эти листы должны быть оформлены так, как показано на рис. 8

Задание 1 Расчеты ведутся по следующим формулам: Надбавка = Оклад * %надбавки / 100 Компенсация = Пост. часть + Оклад * Процент / 100 Премия вводится произвольно Всего начислено = Оклад + Надбавка + Компенсация + Премия • Подоходный налог = Всего начислено * Ставка подоходного налога, % / 100 • Профсоюзный взнос = Всего начислено * Ставка профсоюзного взноса, % / 100 • К выдаче = Всего начислено – Подоходный налог – Профсоюзный взнос • • • 9

Задание 1 • В марте оклад у всех сотрудников повышается на 15%. • Пятый лист должен содержать консолидацию всех сведений о начислениях, удержаниях и выдачи заработной платы для всех сотрудников. Под консолидацией мы будем понимать сумму конкретной позиции на всех листах заданного диапазона, например, сумма начислений за январь, февраль и март. • Оформление листа идентично по отношению к оформлению листов «Январь» , «Февраль» и «Март» . 10

Задание 1 • На этом же листе создать две диаграммы: • суммы начислений заработной платы для всех сотрудников (круговая) – рис. ; • динамика фонда оплаты труда за первый квартал (график) – рис. 11

Задание 2 • Задача планирования производства: 12

Краткая теоретическая часть • Любое мероприятие характеризуется различными параметрами. • На некоторые из них могут напрямую воздействовать участники мероприятия. • Такие параметры или, как принято называть, факторы называют контролируемыми. • Некоторые мероприятия предполагают достижение заранее поставленной цели. • Такие мероприятия принято называть операциями, а их участников – оперирующими сторонами. 13

Задачи исследования операций • Достижение цели может происходить одним единственным доступным путем или существует несколько путей. • Путь к поставленной цели определяется совокупностью контролируемых факторов. • И во втором случае может ставиться задача нахождения наиболее эффективного пути по заданному критерию (минимальное время, минимальные финансовые затраты и т. д. ), т. е. поиска соответствующего набора контролируемых факторов. • Такие задачи называют задачами исследования операций (ЗИО) и науку, которая рассматривает вопросы их решения с применением математических методов, - исследование операций. 14

Задачи исследования операций • Исследование операции предполагает три последовательных этапа: 1. формулирование математической постановки задачи; 2. анализ постановки задачи, определение класса принадлежности и выбор метода решения; 3. решение задачи. 15

Задачи исследования операций • Формулирование постановки задачи в виде математических соотношений является самым сложным этапом, от ее качества зависит эффективность решения. • Математическая постановка задачи исследования операций состоит из двух принципиальных частей: целевой функции (критерия эффективности), значение которой определяет степень достижения цели, и ограничений, которые определяют множество значений контролируемых факторов или область допустимых решений. 16

Задачи исследования операций 17

Задачи линейного программирования 18

Задачи линейного программирования 19

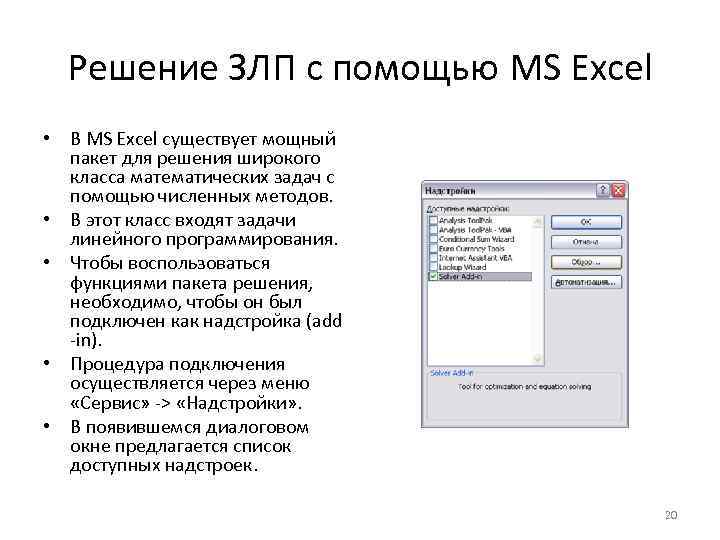
Решение ЗЛП с помощью MS Excel • В MS Excel существует мощный пакет для решения широкого класса математических задач с помощью численных методов. • В этот класс входят задачи линейного программирования. • Чтобы воспользоваться функциями пакета решения, необходимо, чтобы он был подключен как надстройка (add -in). • Процедура подключения осуществляется через меню «Сервис» -> «Надстройки» . • В появившемся диалоговом окне предлагается список доступных надстроек. 20

Решение ЗЛП с помощью MS Excel • Просматривая список, необходимо убедиться, чтобы надстройка «Solver Add-In» (Пакет поиска решения) в нем присутствовала и напротив него стояла галочка. • Когда модуль подключен, то можно приступать к подготовке к решению ЗЛП: заполнение ячеек исходными данными (коэффициенты в целевой функции и в ограничениях) и начальными значениями контролируемых факторов (часто вводят нулевой вектор), расчеты текущего значения целевой функции, промежуточные расчеты в ограничениях. При этом полезной является следующая функция: – СУММПРОИЗВ (список векторов через точку с запятой). • Она вычисляет скалярное произведение векторов. Например, СУММПРОИЗВ(c; x) даст значение, равное , если соответствующие группы смежных ячеек поименованы (присваивать уникальное имя можно не только ячейке, но и группе ячеек). 21

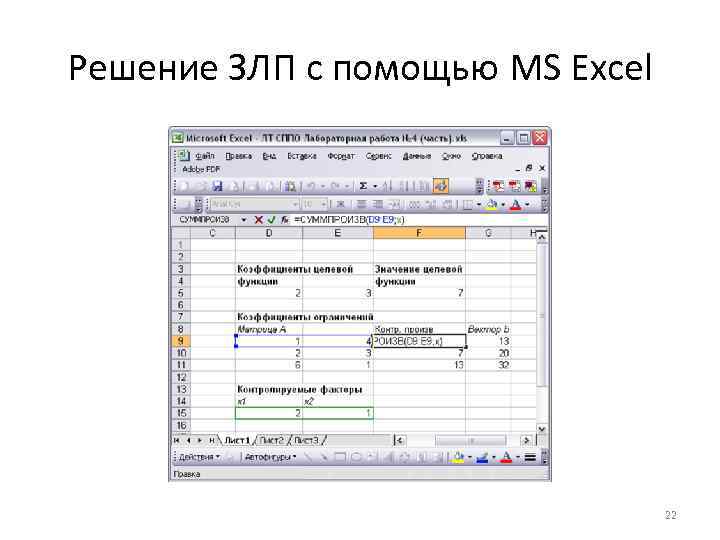
Решение ЗЛП с помощью MS Excel 22

Решение ЗЛП с помощью MS Excel • Расчет значения целевой функции выполнен таким же способом. Контрольные произведения в системе ограничений вычисляется для того, чтобы убедиться, что контролируемые факторы попадают в область допустимых решений (ОДР). • Эти значения (ячейки) также нужны для блока поиска решений. • Когда исходные данные подготовлены, можно приступать к поиску решения. Вызов модуля осуществляется через меню «Сервис» -> «Solver» (поиск решения). 23

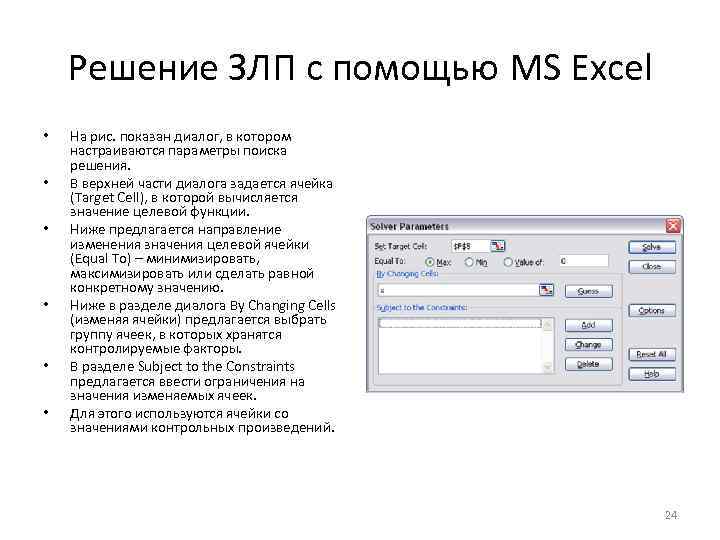
Решение ЗЛП с помощью MS Excel • • • На рис. показан диалог, в котором настраиваются параметры поиска решения. В верхней части диалога задается ячейка (Target Cell), в которой вычисляется значение целевой функции. Ниже предлагается направление изменения значения целевой ячейки (Equal To) – минимизировать, максимизировать или сделать равной конкретному значению. Ниже в разделе диалога By Changing Cells (изменяя ячейки) предлагается выбрать группу ячеек, в которых хранятся контролируемые факторы. В разделе Subject to the Constraints предлагается ввести ограничения на значения изменяемых ячеек. Для этого используются ячейки со значениями контрольных произведений. 24

Решение ЗЛП с помощью MS Excel • Добавление ограничения осуществляется с помощью кнопки Add. • В появившемся диалоге (рис. ) устанавливается ссылка на ячейку с контрольным произведением (Cell Reference) и на ячейку с ограничением (Constraint). • Нажатием кнопки Add можно добавить все необходимые ограничения. 25

Решение ЗЛП с помощью MS Excel • В диалоге Solver Parameters (рис. Слайд 24) необходимо нажать кнопу Options (параметры) в соответствующем окне (рис. ) поставить галочку напротив надписи Assume Linear Model (линейная модель). 26

Решение ЗЛП с помощью MS Excel • После этих настроек можно наживать кнопку Solve и подтвердить/не подтвердить сохранение результатов (рис. ). • Можно заметить, что значения контролируемых факторов изменилось при соблюдении всех ограничений (они были вида «меньше либо равно), а целевая функция увеличилась. 27

Варианты заданий 28

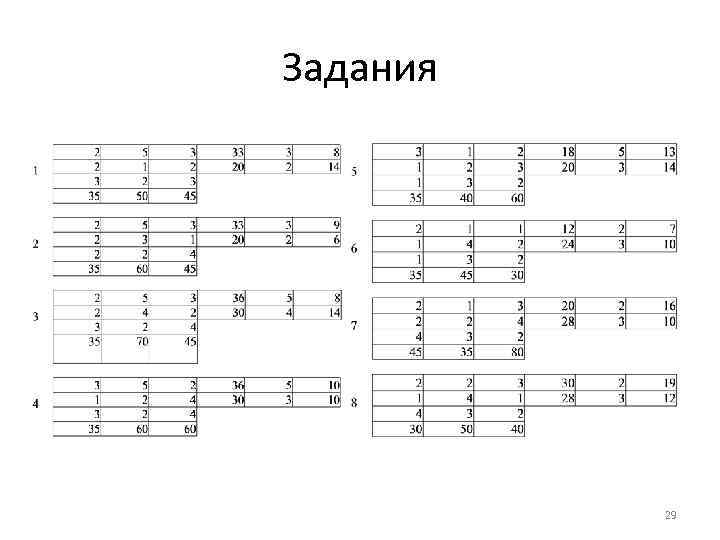
Задания 29

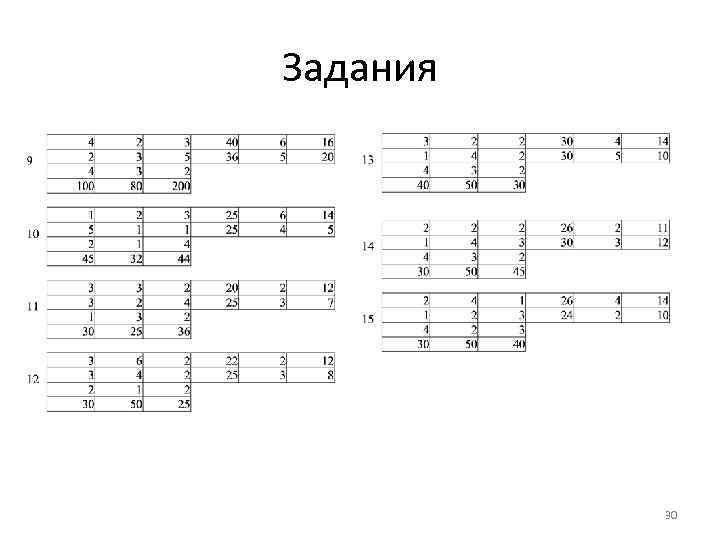
Задания 30