ОСНОВЫ ПРОГРАМИРОВАНИЯ В MATLAB 1 Операторы цикла

ОСНОВЫ ПРОГРАМИРОВАНИЯ В MATLAB 1

Операторы цикла В MATLAB повторяющиеся действия осуществляются с помощью операторов циклов for и while. Самое простое использование for осуществляется следующим образом: 2

For count = start: step: final Команды MATLAB End Здесь count – переменная цикла; n start, final – начальное и конечное действительное значение; n step – шаг из множества действительных чисел (по умолчанию равен 1, его можно опустить). Цикл заканчивается, как становиться больше final. только count 3

Пример 1 Вычислить сумму при x= -1, 0, 1. Решение В редакторе M-file создадим файл-программу. Сохраняем её в файле Summa. m S = 0; for k = 1 : 10 S = S + x. ^ k / factorial(k); End S В командной строке x = -1: 1: 1; Summa S = -0. 6 0 1. 7 Заметим, что переменные k, s глобальные. 4

Удобнее для этого примера использовать файлфункцию. В редакторе М-файлов В командной строке создаем файл-функцию function S = funsum(x, N) > f = funsum (-1 : 1, 10) S = 0; > f = for m = 1 : N -0. 6 0 1. 7 S = S + x. ^ m / factorial(m); end Здесь переменные s, m локальные. 5

Пример 2 Создать матрицу Гильберта порядка n. Решение n = 4; a = zeros (n, n); for i = 1 : n for j = 1: n a (i, j) = 1 / (i+j-1); end a 6

Замечание Перед заполнением матриц и векторов следует сначала создать их и заполнить нулями командой zeros, для увеличения скорости алгоритма (то есть a = zeros (n, n) быстрее, чем a(i, j) = 0, i, j = 1, …, n). 7

Цикл for оказывается полезным, при выполнении повторяющихся действий, когда их число заранее известно. В случае, если их число заранее неизвестно можно воспользоваться циклом while: While условие цикла Команды MATLAB Еnd 8

Пример 3 Найти сумму ряда для заданного x До бесконечности суммировать не удастся, но можно накапливать сумму, пока слагаемые не будут слишком маленькими, например, пока 9

Замечание Малость слагаемого – понятие относительное, слагаемое, может быть, скажем, порядка 10 -10, но и сама сумма того же порядка. В этом случае нельзя останавливать суммирование. Не будем пока обращать на это внимание и вернемся к решению. 10

M-file функция В командной строке function S = mysin(x) > f = mysin (1) S = 0; 0. 8415 k = 0; while abs(x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10 S = S + (-1)^k * x. ^ (2*k + 1)/factorial(2*k + 1); k = k + 1; end 11

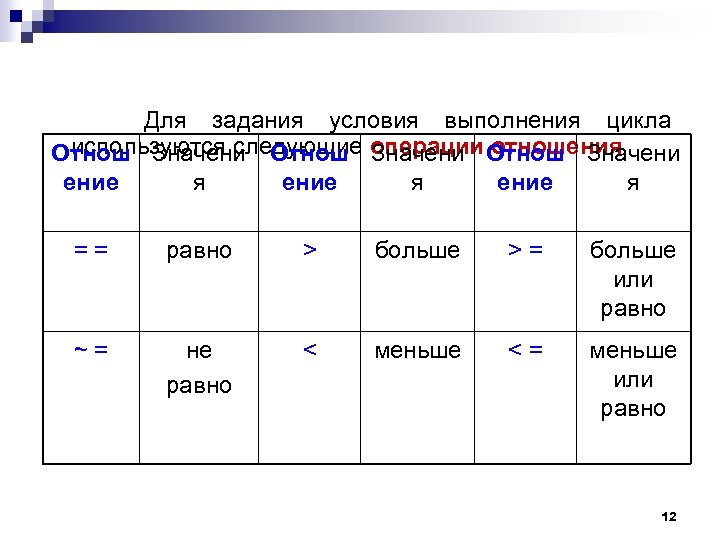
Для задания условия выполнения цикла используются следующие операции отношения Отнош Значени ение я = = равно > больше > = больше или равно ~ = не равно < меньше < = меньше или равно 12

и логические операторы: Оператор Условие Запись в MATLAB Эквивалентная запись Логическое «и» x < 3 и k = 4 and(x < 3, k = =4) (x < 3) & (k = 4) Логическое «или» x = 1 или x = 2 or(x= = 1, x= = 2) (x= = 1) | (x= = 2) Отрицание «не» a ≠ 1. 9 not (a = = 1. 9) ~ (a = = 1. 9) 13

Вернемся к нашему примеру, и заметим, что если ряд расходится, то условие на малость текущего слагаемого может никогда не выполнится и программа зациклиться. Поэтому ограничим число слагаемых 100. 000 Условие будет выглядеть так or (abs (x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10, k <= 100000) Порядок выполнения логических операций позже. 14

Обработка исключительных ситуаций 1) break – прерывание цикла и выполнение оператора следующего за end (например, выход из внутреннего цикла); 2) Часть некорректных математических операций в MATLAB, не приводит к завершению работы программы (например, = inf, = Na. N). Выходом является конструкция try Операторы, выполнение которых может привести к ошибке catch Операторы в случае ошибки end 15

Операторы ветвления Условный оператор В MATLAB используются следующие операторы ветвления: n if – условный оператор; n switch – оператор переключения 16

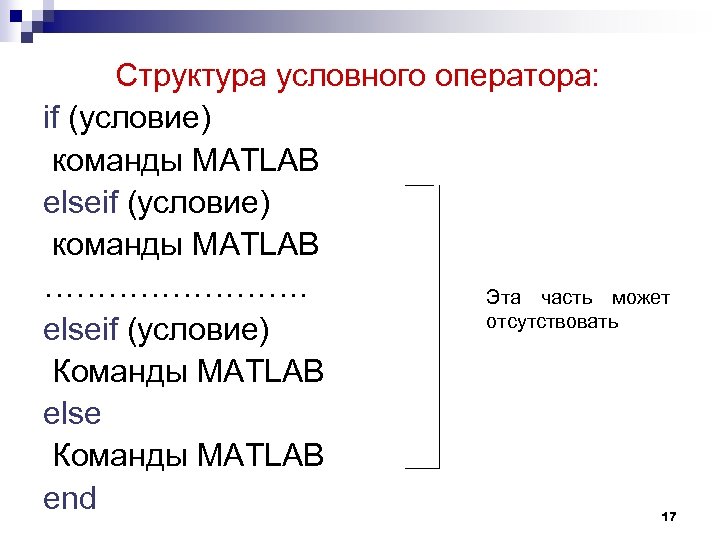
Структура условного оператора: if (условие) команды MATLAB elseif (условие) команды MATLAB …………. Эта часть может отсутствовать elseif (условие) Команды MATLAB else Команды MATLAB end 17

При составлении М-файла, использующего операторы ветвления, полезно применять 1) команду warning (‘текст’) – для вывода предупреждения в командное окно; 2) функцию error (‘текст’) – для прекращения выполнения программы. 18

Пример 4 Дано квадратное уравнение ax 2 + bx +c = 0, a ≠ 0. Напишем М-функцию вычисляющую корни квадратного уравнения. Сделаем проверку на количество входных и выходных параметров, а так же на то, что входные параметры являются числами, а не векторами и матрицами. Более того, учтем случай комплексного корня. Программа выглядит так: 19

function [x 1, x 2] = root 2 (a, b, c) if (nargin <3) error (‘Задайте три коэффициента квадратного уравнения’) end [Na, Ma] = size (a); [Nb, Mb] = size (b); [Nc, Mc] = size (c); if (Na~=1) | (Ma~=1) | (Nb~=1) | (Mb~=1) | (Nc~=1) | (Mc~=1) error (‘Входные аргументы должны быть числами’) end D = b^2 – 4*a*c; If D <0 error (‘Комплексные корни’) end x 1 = (-b + sqrt(D))/2*a; x 2 = (-b – sqrt(D))/2*a; if nargout = = 1 warning (‘Это только один корень’) disp (‘Для получения двух корней используйте’) disp (‘[x 1, x 2] = root 2(a, b, c)’) end 20

Замечание Для написания собственных вычислительных программ большую пользу может принести самостоятельное изучение стандартных файл-функций в подкаталогах Toolbox. Большинство из них имеют открытый код, что позволяет понять принципы программирования в MATLAB. Другие функции (например, cos. m) являются встроенными. Они содержат комментарии об использовании функций. Приведем еще один пример. 21

Пример 5 Вычисление кусочно-заданной функции входным элементом, которой является матрица. Программа выглядит так: 22

function y = kusfun (x) If nargin ~= 1 error (‘Должен быть один входной аргумент’) end [Nx, Mx] = size(x); y = zeros (size(x)); % инициализирует входной аргумент for i = 1 : Nx for j = 1 : Mx if x (i, j) <-pi y (i, j) = sin (x (i, j)) – 1; elseif x (i, j) < pi % проверка x >= -pi не нужна! y (i, j) = x (i, j) / pi; else y (i, j) = - cos(x (i, j)) end end 23

Оператор switch удобно применять тогда, когда есть соответствие между дискретными значениями некоторой переменной и последующими действиями. 24

Структура оператора видна из следующего примера: switch a case -1 disp (‘a = -1’) case 0 disp (‘a = 0’) otherwise disp (‘a не равно -1, 0’) end 25

Оператор switch хорошо подходит для решения поставленной задачи о выводе различных графиков исследуемой функции (каркасная поверхность (а=1), линии уровня (а=2) и т. д. ). 26

Логические выражения с массивами и числами Универсальным способом обработки матричных данных служат логические операции. Поскольку MATLAB представляет числа массивами 1 1, то естественно ожидать, что массивы могут входить в логические выражения. Сейчас мы рассмотрим расширение логических операций и операций отношения на случай массивов. 27

Операции отношения Результат операции отношения в MATLAB может быть или логическая единица (‘истина’) или логический нуль (‘ложь’). Причем в отличие от многих языков программирования арифметические переменные могут использоваться в одном выражении с логическими. 28

Пример 6 • > a = 1; b = 3; c = 1; > a + (b > c) ans = 2 > a + (b<=c) ans = 1 29

• > A = [1 2; 3 4]; B = [1 3; 4 5]; > C = A = = B C = 30

Замечание Так же как и в поэлементных арифметических операциях, допустимо использовать числа в качестве одного из аргументов операции отношения. В этом случае происходит сравнение каждого элемента массива с числом, результатом является массив того же размера, что и исходный. 31

Логические операции Применение логических операций к массивам приводит к поэлементному их выполнению над элементами массивов. n А and B – дает единицу, если соответствующие элементы не равны нулю; n A or B - дает единицу, если хотя бы один элемент не равен нулю; 32

not A – применяется к одному массиву, если элемент не равен нулю, то ставится нуль, иначе – единица; n all (v) – проверка наличия нулевых элементов в векторе, возвращает единицу, если нет нулевых элементов. Если v – матрица, то результат по столбцам; n any (v) – возвращает единицу, если во входном векторе есть хотя бы один ненулевой элемент. n 33

Приоритет операций 1. Отрицание; 2. Транспонирование, возведение в степень (в том числе поэлементное), знак плюс и минус перед числом; 3. Умножение и деление (в том числе поэлементное); 4. Сложение и вычитание; 5. Операции отношения; 6. Логическое ‘и’, логическое ’или’. 34

Логическое индексирование Выделение части массива, элементы которого удовлетворяют определенному условию производится функцией find. 35

Пример 7 > a = [2 3 0 -1 0 3]; > u = find ((a < 1) & (a >= -1)) 3 4 5 > anew = a(u) 0 -1 0 36

Пример 8 Заменить самостоятельно элементы квадратной матрицы 5 x 5 случайных чисел из интервала (0, 1), больших среднего значения всех элементов на 10%, на среднее значение. Решение > A = rand (5); > S = sum (sum A) / 25; > A(find (A > S* 1. 1)) = S В данном случае функция find выдает 2 вектора номера строк и номера столбцов. 37

Полиномы в MATLAB Полином p (х) =anxn+an-1 xn-1+. . . +a 0, an≠ 0 в MATLAB задается вектор-строй р=[an, an-1, . . . , a 0] , где ai – любые комплексные числа, an≠ 0. Заметим, что степень полинома вычисляется так: n=length(р)-1 (при n=0 получается const). 38

Основные команд для действий с полиномами таковы: n n n r=roots(р) – вектор-столбец, содержащий все корни полинома; p=poly(r) – построение полинома по корням, заданным в векторе-столбце r, причем, если r квадратная матрица, то р - характеристический многочлен; y=polyval(p, x) – поэлементное вычисление у значений полиному р на множестве х, где х может быть вектором или матрицей; 39

n n n polyder(p) – вектор-строка, производная от p (дифференцирование полинома p); polyder(p, q) –производная от произведения полиномов p и q; [a, b]= polyder(p, q) – производная от частного полиномом p и q, где a и b являются числителем и знаменателем получившейся дроби; 40

n n n p=polyfit(x, y, n) – приближение функции y(x) полиномом p n-й степени по методу, минимизирующему расстояние между графиком полинома и истиной кривой, усредненное по всей их длине; conv(p, q) – вектор-строка, произведение полиномов p и q; [w, r]=deconv(p, q) – деление p на q, причем w-частное, r-остаток и p=conv (q, w) +r; 41

n [r, p, k]=residue(a, b) – разложение рациональной функции на простые дроби над полем комплексных чисел с выделением целой части k(х) или где ri – вычеты (элементы r), pi – полюса (элементы p). Эта команда работает и в обратную строну [a, b] =residue(r, p, k) 42

Замечание 1. Если в residue (a, b) полином b(х), а в roots(p) полином р(х) имеют кратные или близкие друг к другу корни, то результаты могут быть неверными, поскольку такая задача плохо обусловлена. Плохая обусловленность – это крайне сильная зависимость результата от коэффициентов (аналог устойчивости решения в дифференциальных уравнениях). 43

2. При работе с полиномами возникают полиномы вида [0, . . . ], а MATLAB автоматически не проверяет an≠ 0, и возникают ошибки (нужно самим следить). 44