Основы молекулярной физики и термодинамика Молекулярная физика

Основы молекулярной физики и термодинамика Молекулярная физика

• Молекулярная физика – раздел физики, в котором изучаются физические и физико химические свойства макроскопических тел в различных агрегатных состояниях, исходя из молекулярно кинетических представлений об их строении. • Молекулярная физика основывается на трех основных положениях: • Все макроскопические тела состоят из очень большого числа частиц – молекул (атомов); • Молекулы находятся в непрерывном хаотическом движении (тепловое движение); • Молекулы взаимодействуют друг с другом, притягиваясь на больших и отталкиваясь на малых расстояниях.

Разделами молекулярной физики являются: физика газов, физика жидкостей, физика твердых тел, физика конденсированных систем (полимеры, жидкие кристаллы, наночастицы и др. ). • В них рассматриваются: строение вещества в различных агрегатных состояниях и его изменение под влиянием внешних факторов (давления, температуры, электрических и магнитных полей), поведение вещества в экстремальных условиях, релаксационные процессы, фазовые переходы (конденсация, кристаллизация, испарение, плавление и др. ), явления переноса (диффузия, теплопроводность, вязкость), критическое состояние вещества, поверхностные явления на границе раздела фаз. • • •

• Термодинамика – это наука о тепловых явлениях. • В противоположность молекулярно кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. • Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно кинетические модели для иллюстрации своих выводов.

• Общим для всех разделов молекулярной физики является теоретический подход, основанный на применении феноменологического (термодинамического) и статистического (молекулярного) методов исследования. • Хотя эти методы качественно различны, они тесно связаны и взаимно дополняют друга. • Термодинамический метод основан на началах термодинамики, имеющих общий характер и не использующих представления о молекулярном строении вещества. • Молекулярно кинетический подход подразумевает рассмотрение конкретной молекулярной модели вещества. • Несмотря на внешние различия этих методов, они внутренне связаны между собой, поскольку все выводы, полученные из рассмотрения частных молекулярных моделей, должны согласовываться с общими выводами термодинамики.

• Атомы и молекулы, взаимодействую друг с другом, образуют разнообразные вещества (системы). • Если число частиц невелико (десятки, сотни), то мы имеем микросистему. • Если число частиц системы во много раз больше (миллионы и более), то такую систему называют макросистемой. Например, газ, состоящий из очень большого числа молекул — это макросистема. • Большое число частиц системы приводит к появлению у нее новых свойств, которыми отдельные частицы не обладают. Например, давление газа есть результат непрерывного действия всех молекул на стенки сосуда, хотя не каждая молекула сталкивается со стенками.

• Для описания состояния макросистемы вводят параметры, которые называются параметрами состояния. • Различают микропараметры и макропараметры состояния. • Микропараметры — это параметры, характеризующие отдельную частицу. Например, масса молекулы, ее скорость, энергия. • Макропараметры — это параметры, характеризующие систему в целом. Например, объем V, давление p, средняя скорость молекул , температура T, концентрация n и т. д. Значения этих параметров могут быть установлены с помощью измерительных приборов.

• Объем газа V — это объем сосуда, в котором газ находится. В СИ измеряется в м 3. Часто используется несистемная единица измерения 1 литр: 1 л = 10 3 м 3. • Давление р — скалярная физическая величина, равная отношению силы F к значению площади S площадки, на которую эта сила действует. • Газ оказывает давление вследствие столкновений молекул со стенками сосуда. В СИ единица давления 1 Н/м 2 = 1 Па (Паскаль). • Внесистемные единицы измерения — 1 мм. рт. ст и 1 атмосфера. • Нормальное давление равно одной физической атмосфере. • 1 физическая атмосфера = 1 атм = 760 мм. рт. ст. • 1 мм. рт. ст. = 133 Па.

• Температура — скалярная физическая величина вводится для количественной характеристики внутренней энергии тела. Опыт показывает, что она характеризует состояние теплового равновесия тела. • По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (°С). За 1 °С принята одна сотая промежутка от температуры плавления льда (0 °С) до температуры кипения воды (100 °С). • Абсолютная температурная шкала — шкала температур, в которой за начало отсчета принят абсолютный нуль. Температура здесь обозначается буквой T, измеряется в кельвинах (К). За единицу измерения в этой шкале принят один градус Цельсия, т. е. изменение на один кельвин (1 К) равно изменению на один градус Цельсия. • T = (t + 273) К или t = (T – 273) °С, • где T — абсолютная термодинамическая температура (К); t — температура по шкале Цельсия (°С).

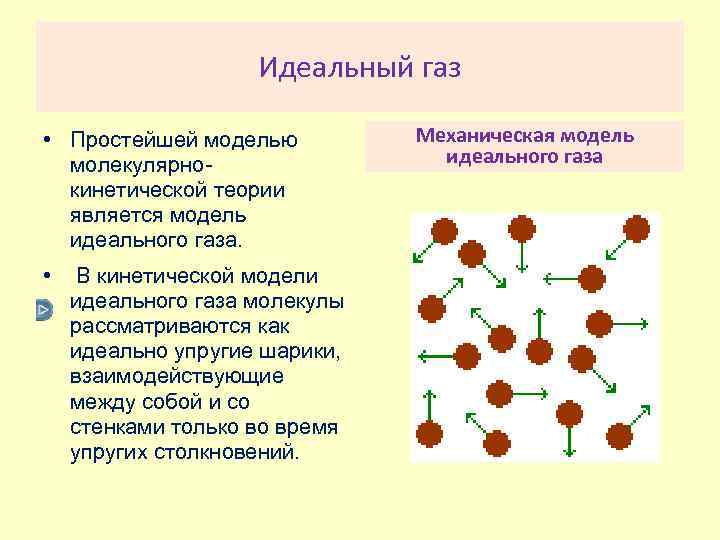Идеальный газ • Простейшей моделью молекулярнокинетической теории является модель идеального газа. • В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Механическая модель идеального газа

Идеальный газ • Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. • Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур.

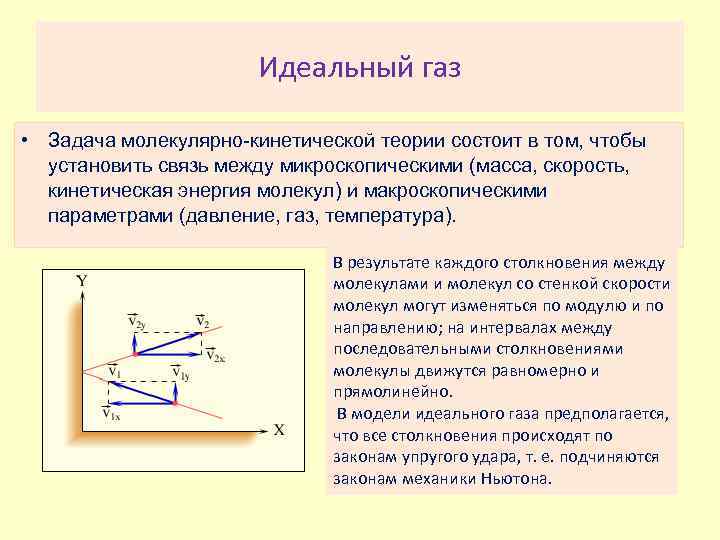Идеальный газ • Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, газ, температура). В результате каждого столкновения между молекулами и молекул со стенкой скорости молекул могут изменяться по модулю и по направлению; на интервалах между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

Состояние системы • Система состоит из совокупности тел. • Тела, не входящие в систему, называют окружающей средой. • Дан газ (система) в закрытом цилиндре под поршнем (окружающая среда). • Изменение положения поршня или температуры изменяют состояние системы.

Состояние системы • Величины, характеризующие состояние системы, называются ее параметрами. • Состояние таких простейших систем, как газ, характеризуется следующими макроскопическими параметрами: • объемом V, давлением р, температурой Т.

Состояние системы •

Состояние системы • Если внешние условия неизменны, то система с течением времени приходит в равновесное состояние: выравниваются давления и температуры ее отдельных систем. • В равновесном состоянии системы между параметрами имеется связь: заданные два параметра системы (например, ее температура и объем) однозначно определяют третий (давление). • F(V, p, T)= 0 – уравнение состояния.

Состояние системы Равновесное состояние может быть изображено точкой на плоскости. Под процессом понимается всякий переход системы из одного состояния в другое. При бесконечно медленном протекании процесса можно считать, что в каждый данный момент времени состояние системы равновесно. Такой процесс называют равновесным процессом и его можно представить себе как последовательность равновесных состояний.

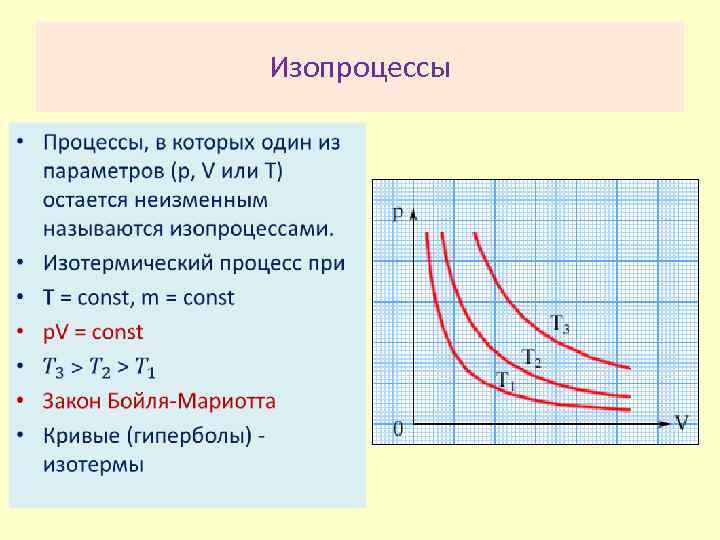Изопроцессы •

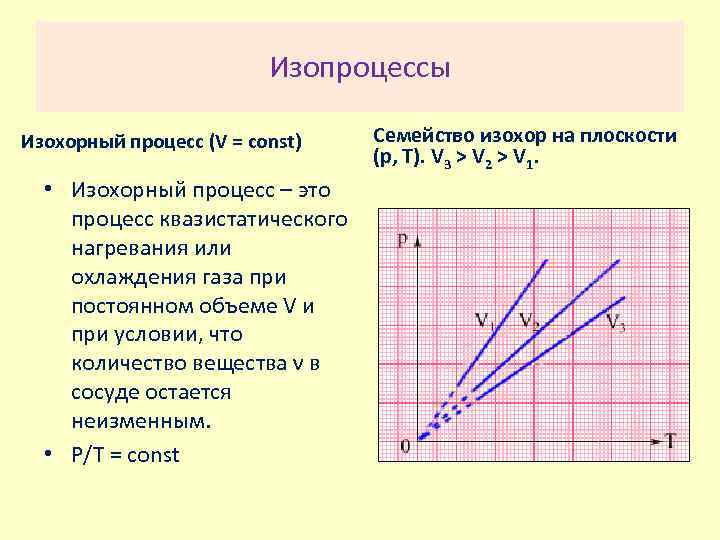Изопроцессы Изохорный процесс (V = const) • Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным. • P/T = const Семейство изохор на плоскости (p, T). V 3 > V 2 > V 1.

Закон Шарля • Уравнение изохорного процесса называется законом Шарля и может быть записано в виде: • где p 0 – давление газа при T = T 0 = 273, 15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273, 15) К– 1, называют температурным коэффициентом давления.

Изопроцессы Изобарный процесс p=const • • В области низких температур все изобары идеального газа сходятся в точке T=0. Но это не означает, что объем реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может. Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.

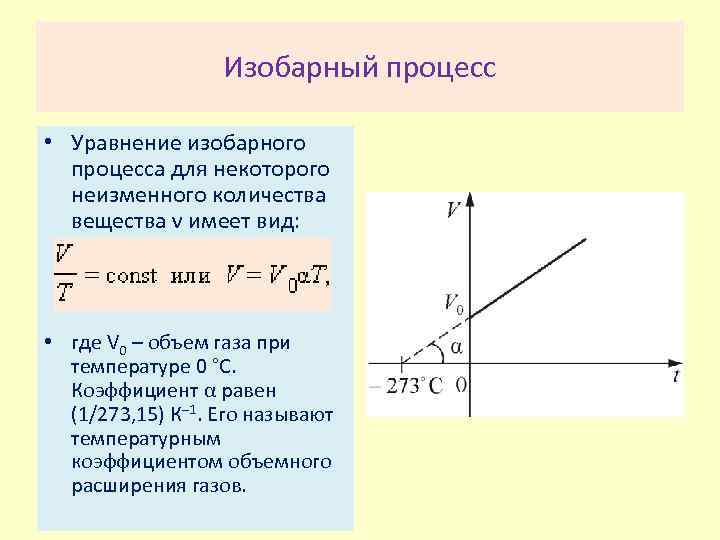Изобарный процесс • Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид: • где V 0 – объем газа при температуре 0 °С. Коэффициент α равен (1/273, 15) К– 1. Его называют температурным коэффициентом объемного расширения газов.

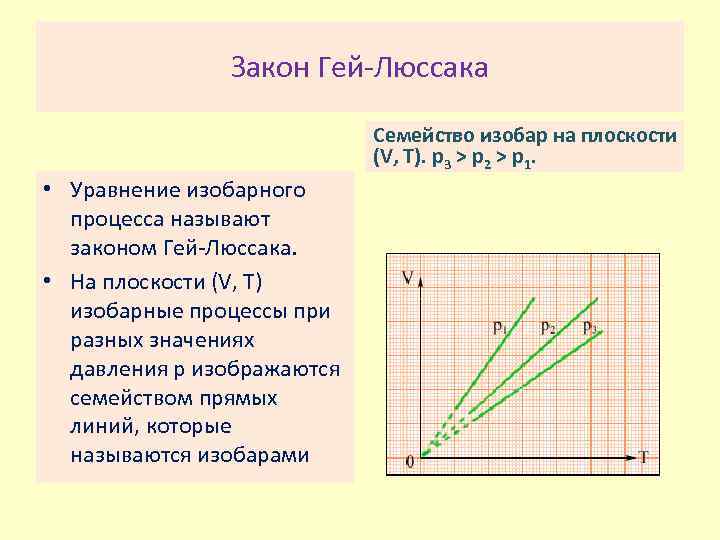Закон Гей Люссака Семейство изобар на плоскости (V, T). p 3 > p 2 > p 1. • Уравнение изобарного процесса называют законом Гей Люссака. • На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий, которые называются изобарами

Закон Авогадро •

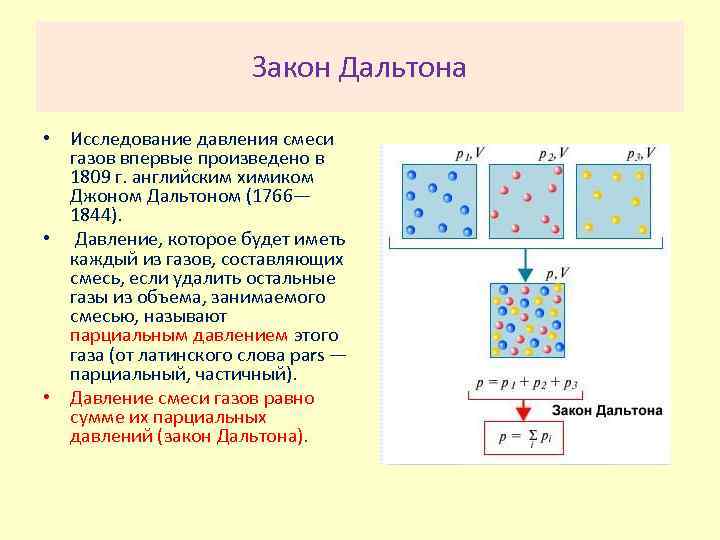Закон Дальтона • Исследование давления смеси газов впервые произведено в 1809 г. английским химиком Джоном Дальтоном (1766— 1844). • Давление, которое будет иметь каждый из газов, составляющих смесь, если удалить остальные газы из объема, занимаемого смесью, называют парциальным давлением этого газа (от латинского слова pars — парциальный, частичный). • Давление смеси газов равно сумме их парциальных давлений (закон Дальтона).

Уравнение Клапейрона Менделеева • Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля Мариотта, Шарля и Гей Люссака для данной массы газы уравнение Клапейрона

Уравнение Клапейрона Менделеева •

Уравнение Клапейрона Менделеева •

Давление идеального газа •

Основное уравнение молекулярно кинетической теории идеальных газов •

•

•

•

•

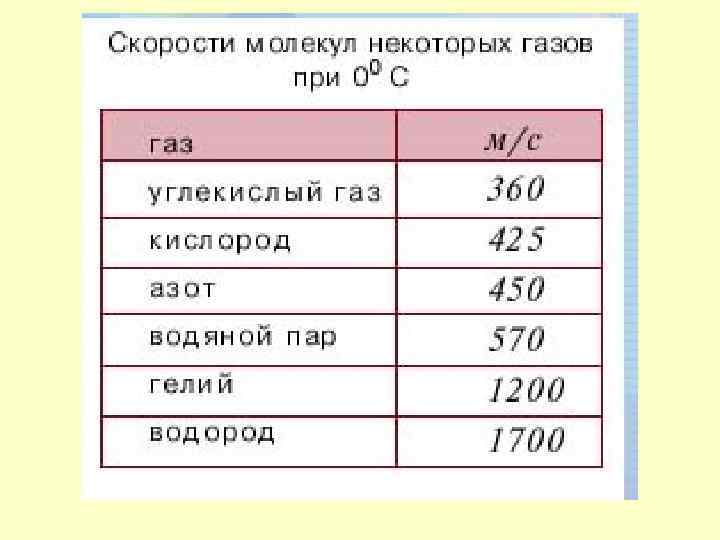
Закон Максвелла для распределения молекул идеального газа по скоростям • Из за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направ лении в среднем движется одинаковое число молекул. • Средняя квадратичная скорость молекул массой т0 в газе, находящемся в состоянии равновесия при Т= const. остается постоянной и равной • В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоро стям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом (1831 1849).

• Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. • Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул d. N(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул d. N(v)/N, скорости которых лежат в интервале от v до v+dv, • т. е.

• Применяя методы теории вероятностей, Максвелл нашел функцию f(v) – закон распределения молекул идеального газа по скоростям • Выводы: • Вид распределения молекул газа по скоростям для каждого газа зависит от рода газа (m) и от параметра состояния (Т). Давление P и объём газа V на распределение молекул не влияют.

• В показателе степени стоит отношение • т. е. кинетической энергии, соответствующей данной скорости υ к (k. Т) – средней энергии теплового движения молекул при данной температуре, значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии (то есть показывает, какова вероятность при данной температуре иметь именно такое значение кинетической энергии).

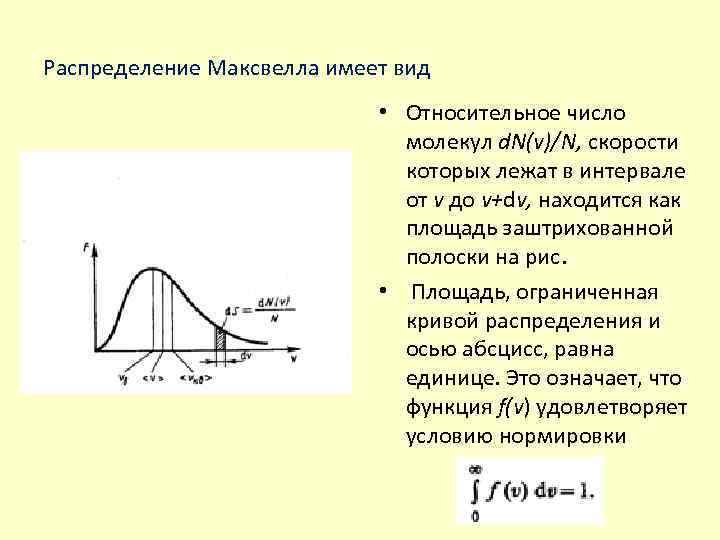Распределение Максвелла имеет вид • Относительное число молекул d. N(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рис. • Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки

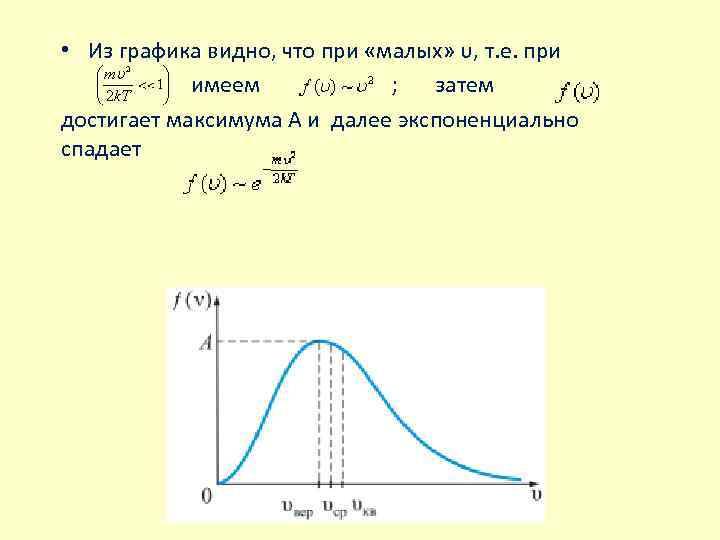• Из графика видно, что при «малых» υ, т. е. при имеем ; затем достигает максимума А и далее экспоненциально спадает

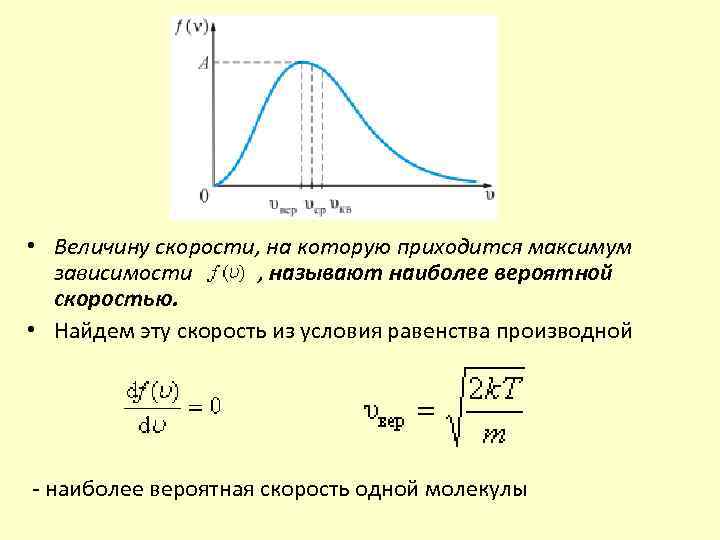• Величину скорости, на которую приходится максимум зависимости , называют наиболее вероятной скоростью. • Найдем эту скорость из условия равенства производной наиболее вероятная скорость одной молекулы

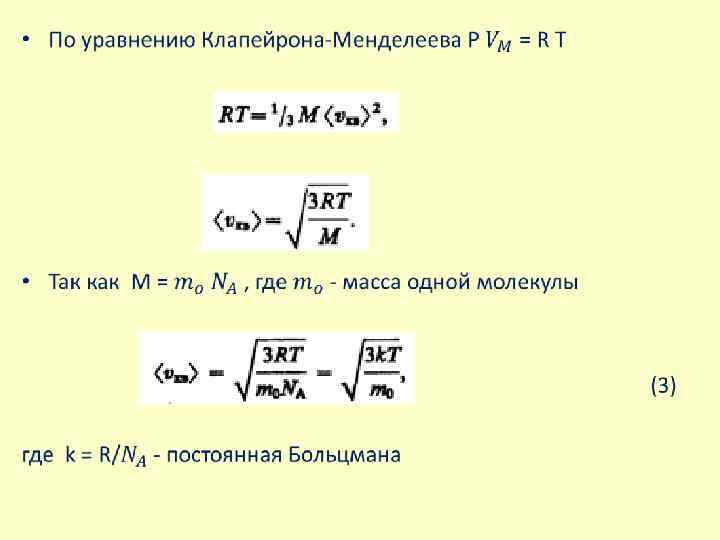
• Для одного моля газа: • где µ молярная масса, m – масса молекулы • Среднюю квадратичную скорость найдем, используя • соотношение • для одной молекулы, • для одного моля газа

• Средняя арифметическая скорость: • где число молекул со скоростью от υ до υ+dυ. Если подставить сюда f(υ) и вычислить, то получим: • для одной молекулы, • для одного моля газа

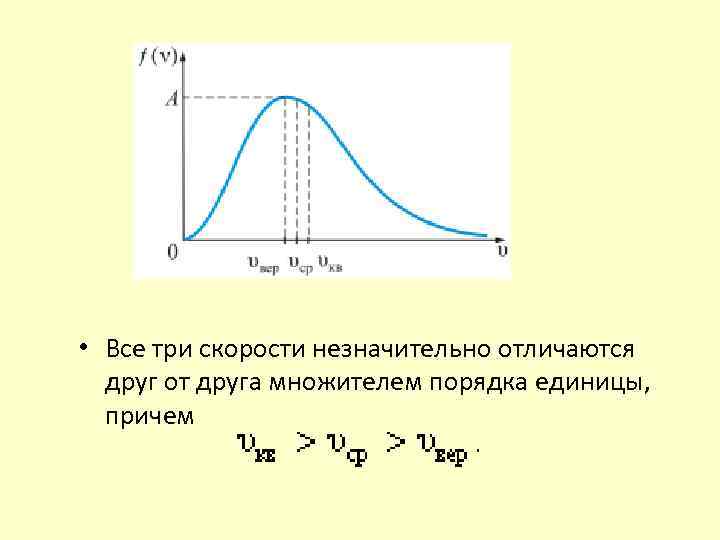• Все три скорости незначительно отличаются друг от друга множителем порядка единицы, причем

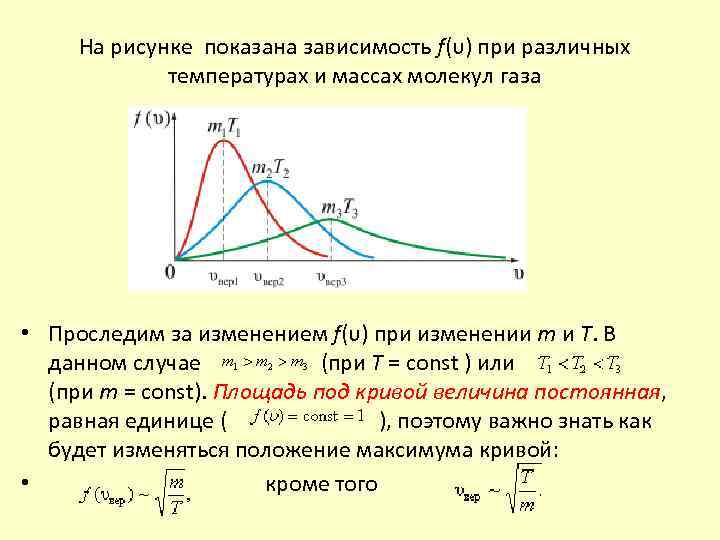На рисунке показана зависимость f(υ) при различных температурах и массах молекул газа • Проследим за изменением f(υ) при изменении m и T. В данном случае (при T = const ) или (при m = const). Площадь под кривой величина постоянная, равная единице ( ), поэтому важно знать как будет изменяться положение максимума кривой: • кроме того

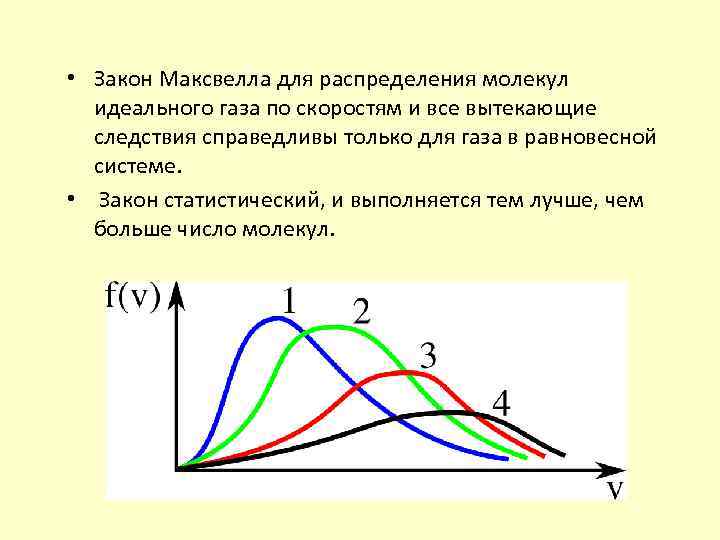• Закон Максвелла для распределения молекул идеального газа по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. • Закон статистический, и выполняется тем лучше, чем больше число молекул.

Распределение Больцмана • В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана: • n = n 0 exp( mgh / k. T ) • где n концентрация молекул на высоте h, • n 0 концентрация молекул на начальном уровне h = 0, • m масса частиц, • g ускорение свободного падения, • k постоянная Больцмана, • T температура

Распределение Больцмана • Анимация показывает схематически движение молекул газа в присутствии гравитационного поля. • Мы можем видеть, что концентрация молекул у дна сосуда оказывается выше, чем концентрация в верхней части сосуда. • Под действием теплового движения молекулы подбрасываются вверх, а затем падают вниз за счет действия сил тяжести.

• Если высота сосуда много меньше чем k. T/mg, то зависимостью концентрации от высоты можно пренебречь. С другой стороны, в атмосфере концентрация молекул быстро уменьшается с увеличением высоты и, поэтому, величина атмосферного давления также уменьшается. • Принимая во внимание, что P = nk. T, мы можем записать так называемую барометрическую формулу, описывающую изменение атмосферного давления в зависимости от высоты: P = P 0 exp( mgh / k. T ) • Измеряя давление за бортом самолёта, мы можем вычислить при помощи барометрической формулы приблизительную высоту полёта.

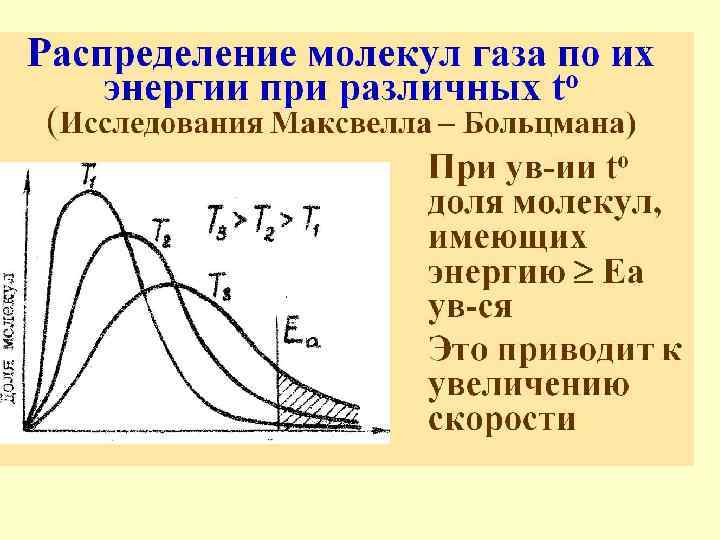
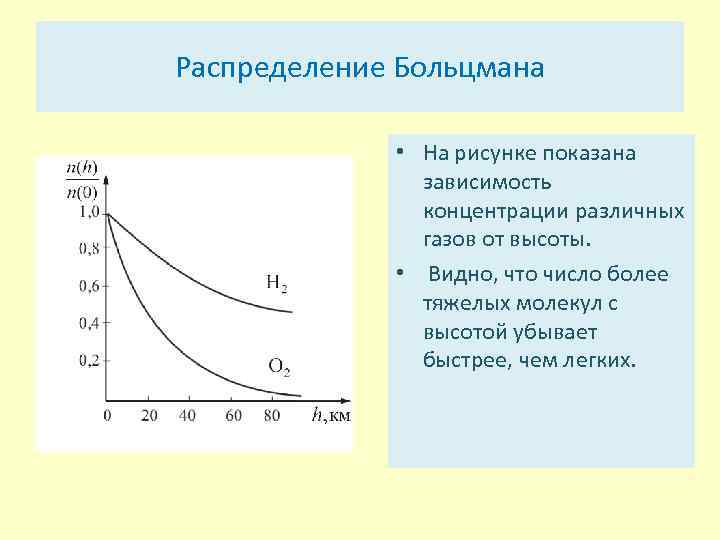Распределение Больцмана • На рисунке показана зависимость концентрации различных газов от высоты. • Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

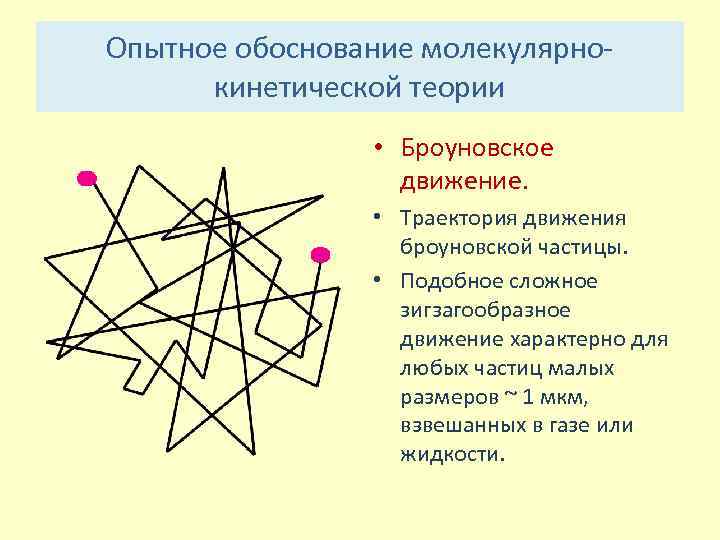Опытное обоснование молекулярно кинетической теории • Броуновское движение. • Траектория движения броуновской частицы. • Подобное сложное зигзагообразное движение характерно для любых частиц малых размеров ~ 1 мкм, взвешанных в газе или жидкости.

Броуновское движение • В 1827 год шотландский ботаник Броун (1773 1858), занимаясь изучением поведения цветочной пыльцы под микроскопом , обнаружил, что отдельные споры совершают абсолютно хаотичные импульсные движения. • Он определил, что эти движения никак не связаны ни с завихрениями и токами воды, ни с ее испарением, после чего, описав характер движения частиц, честно расписался в собственном бессилии объяснить происхождение этого хаотичного движения. Однако, будучи дотошным экспериментатором, Броун установил, что подобное хаотичное движение свойственно любым микроскопическим частицам.

Броуновское движение • Лишь в 1905 году Альберт Эйнштейн установил, что это явление служит наилучшим экспериментальным подтверждением правоты атомной теории строения вещества. • Он объяснил его примерно так: взвешенная в воде спора подвергается постоянной «бомбардировке» со стороны хаотично движущихся молекул воды.

Броуновское движение • В среднем, молекулы воздействуют на нее со всех сторон с равной интенсивностью и через равные промежутки времени. Использовав законы математической статистики и молекулярно кинетической теории газов, Эйнштейн вывел уравнение, описывающее зависимость среднеквадратичного смещения броуновской частицы от макроскопических показателей, будь то пыльца растений, взвеси минералов или вообще любая измельченная субстанция.

Броуновское движение • Интенсивность броуновского движения повышается с ростом температуры, с уменьшением вязкости и размеров частиц. • Броуновское движение взвешенных частиц вызывается ударами молекул среды.

Первое экспериментальное определение скорости молекул. Опыты Штерна.

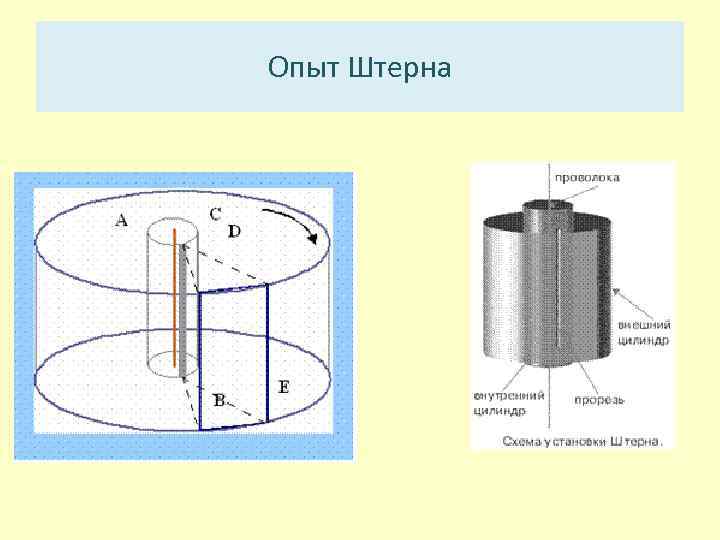
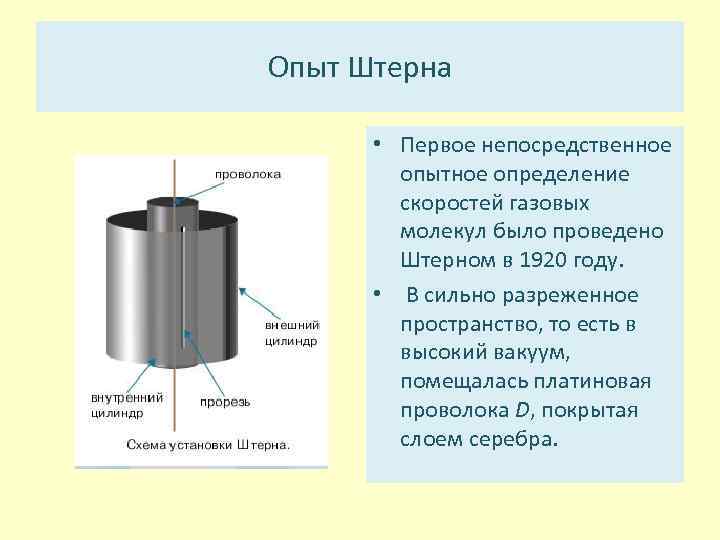Опыт Штерна • Первое непосредственное опытное определение скоростей газовых молекул было проведено Штерном в 1920 году. • В сильно разреженное пространство, то есть в высокий вакуум, помещалась платиновая проволока D, покрытая слоем серебра.

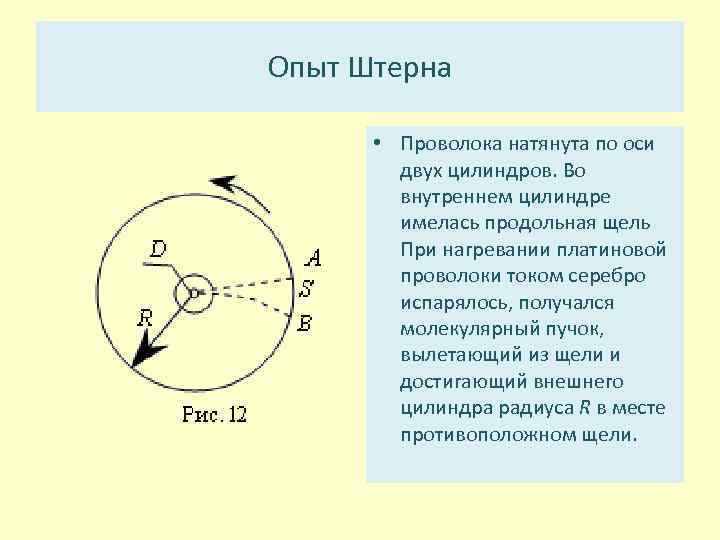Опыт Штерна • Проволока натянута по оси двух цилиндров. Во внутреннем цилиндре имелась продольная щель При нагревании платиновой проволоки током серебро испарялось, получался молекулярный пучок, вылетающий из щели и достигающий внешнего цилиндра радиуса R в месте противоположном щели.

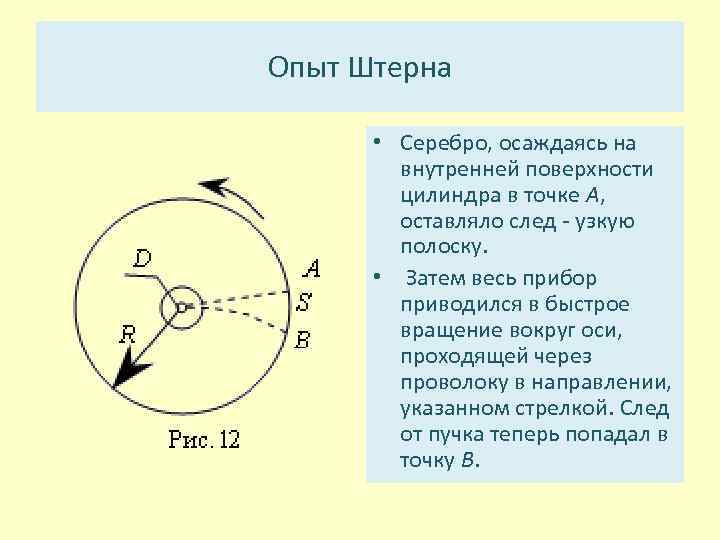Опыт Штерна • Серебро, осаждаясь на внутренней поверхности цилиндра в точке А, оставляло след узкую полоску. • Затем весь прибор приводился в быстрое вращение вокруг оси, проходящей через проволоку в направлении, указанном стрелкой. След от пучка теперь попадал в точку В.

• Легко связать это смещение S со скоростью молекул v. Молекулы достигают стенки за время t, равное . • За это время каждая точка на стенке сосуда пройдет путь • где угловая скорость вращения прибора. • Из этого выражения получим время t: Приравнивая выражение для времени, получим или

• По формуле рассчитывали скорость. • Но след в точке В был не таким, как в точке А, он был размазан. • Этого и следовало ожидать, так как атомы серебра вылетают с различными скоростями. • Измерение плотности осевшего серебра позволило подтвердить справедливость распределения Максвелла молекул по скоростям.

Опыт Штерна

• Температура нити в опытах Штерна равнялась 1200 °С, что соответствует среднеквадратичной скорости • В эксперименте для этой величины получилось значение от 560 до 640 м/с. Кроме того, изображение щели всегда оказывалось размытым, что указывало на то, что атомы Ag движутся с различными скоростями. • Таким образом, в этом опыте были не только измерены скорости газовых молекул, но и показано, что они имеют большой разброс по скоростям. Причина – в хаотичности теплового движения молекул. Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь друг с другом, как то «распределяются» по скоростям, причём вполне определённым образом.