Основы математического моделирования Статистический анализ взаимосвязи и взаимозависимости

Основы математического моделирования Статистический анализ взаимосвязи и взаимозависимости признаков: корреляционный анализ, регрессионный анализ (линейные корреляции, подгонка кривых), расчёт отношений шансов и рисков.

Анализ взаимосвязи различных признаков очень часто встречается в процессе обработки данных биомедицинских исследований. В самом деле, нередко бывает необходимо строго доказать взаимосвязь между неким воздействием и изучаемым эффектом ( «исходом» ), а также оценить силу и характер подобной взаимосвязи.

Корреляционный анализ Корреляция – статистическая взаимосвязь двух параметров между собой; сила этой вза имосвязи измеряется т. н. коэффициентом корреляции. Коэффициент корреляции (r) – показывает, в какой степени значения одного признака изменяются при пропорциональном изменении значений другого признака. Изменяется от 1 до +1. Ноль – отсутствие корреляции. Прямая, обратная корреляции. | r | ≤ 0, 25 – слабая корреляция 0, 25 < | r | < 0, 75 – умеренная корреляция | r | ≥ 0, 75 – сильная корреляция Корреляция: статистически значимая, но клинически незначимая (R≤ 0, 25). Клинически значимая, но статистически незначимая (p>0, 05; малый размер выборки).

В малых выборках высока вероятность выявления взаимосвязей, обусловленных исключительно случайным сочетанием значений параметров, причем меньше размер выборки, тем выше роль случайности в результатах статистической обработки. Статистическая обработка данных, полученных при анализе выборок, включающих менее 20 наблюдений, почти всегда не имеет смысла.

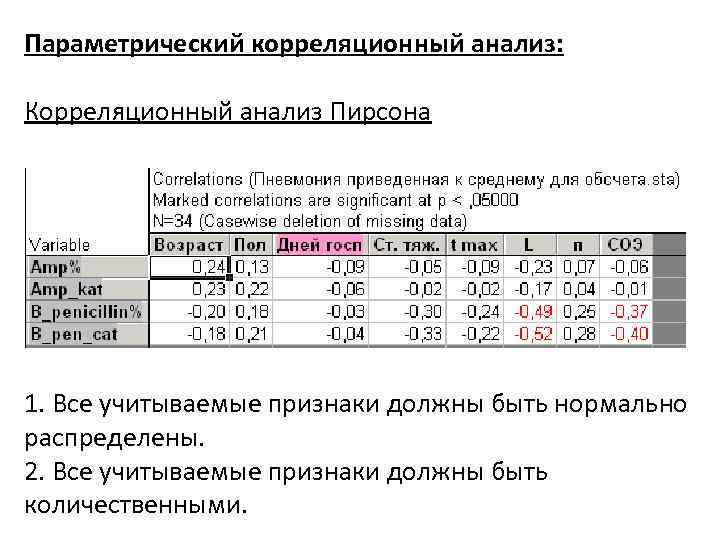Параметрический корреляционный анализ: Корреляционный анализ Пирсона 1. Все учитываемые признаки должны быть нормально распределены. 2. Все учитываемые признаки должны быть количественными.

Непараметрический корреляционный анализ: Корреляционный анализ Спирмена, Кендалла, Гамма 1. Количественные признаки, распределение хотя бы одного из них не является нормальными либо неизвестно. 2. Смесь количественных и порядковых признаков. 3. Несколько порядковых признаков. Ранговая корреляция Спирмена (ρ) – универсальный метод, используется для оценки взаимосвязи количественных (независимо от вида распределения) и/или порядковых признаков.

Ранговая корреляция Тау Кендалла (τ): используется для оценки взаимосвязи порядковых признаков или смеси количественных и порядковых признаков. Гамма-корреляция (γ): используется, когда в переменных имеется много совпадающих значений.

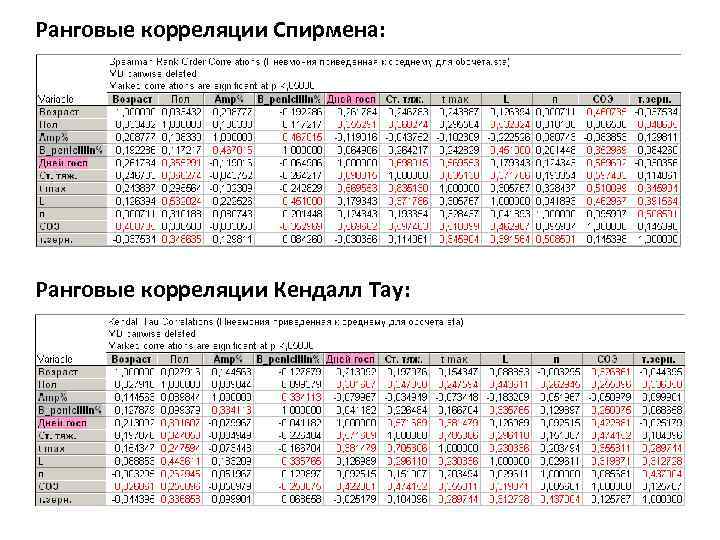Ранговые корреляции Спирмена: Ранговые корреляции Кендалл Тау:

Доверительный интервал для коэффициента корреляции 1. Вычисляется функция z: 2. Вычисляется стандартная ошибка m для z: n – количество наблюдений в выборке, для которых рассчитывается коэффициент корреляции. 3. Вычисляются нижняя и верхняя границы (z 1 и z 2) величины z: t – значение t критерия для данного числа степеней свободы и заданного уровня значимости.

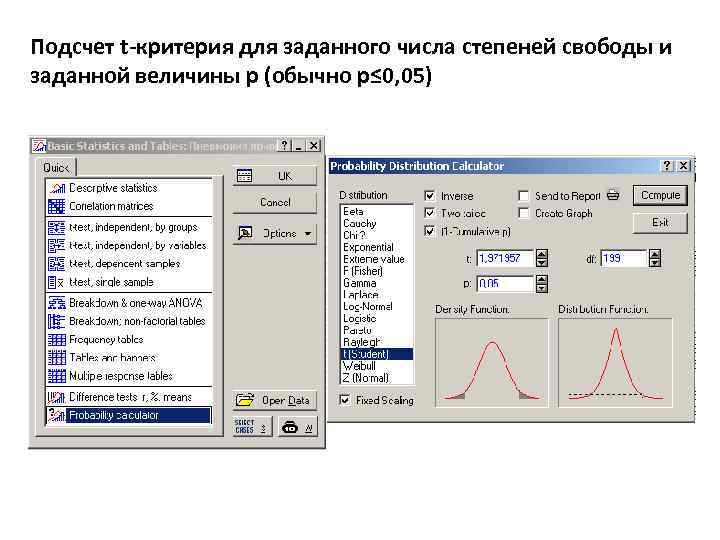Подсчет t-критерия для заданного числа степеней свободы и заданной величины р (обычно р≤ 0, 05)

Доверительный интервал для коэффициента корреляции 4. Вычисляются нижний и верхний пределы ДИ для коэффициента корреляции r: С вероятностью 95% истинное значение коэффициента корреляции находится в указанных границах.

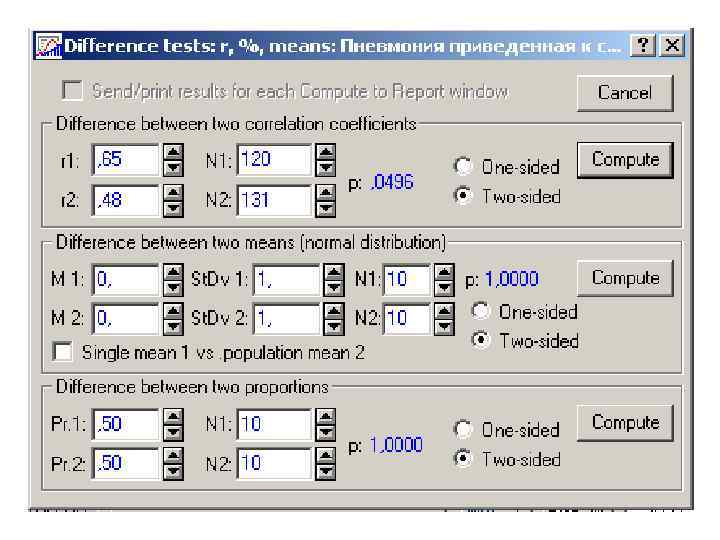
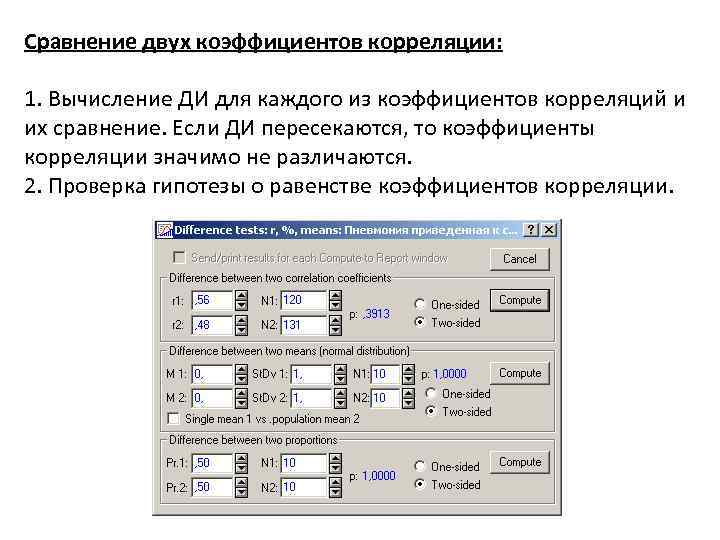Сравнение двух коэффициентов корреляции: 1. Вычисление ДИ для каждого из коэффициентов корреляций и их сравнение. Если ДИ пересекаются, то коэффициенты корреляции значимо не различаются. 2. Проверка гипотезы о равенстве коэффициентов корреляции.

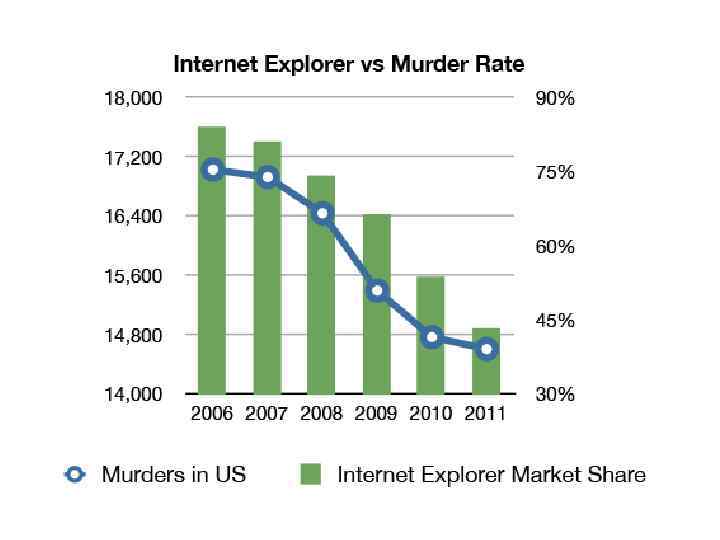
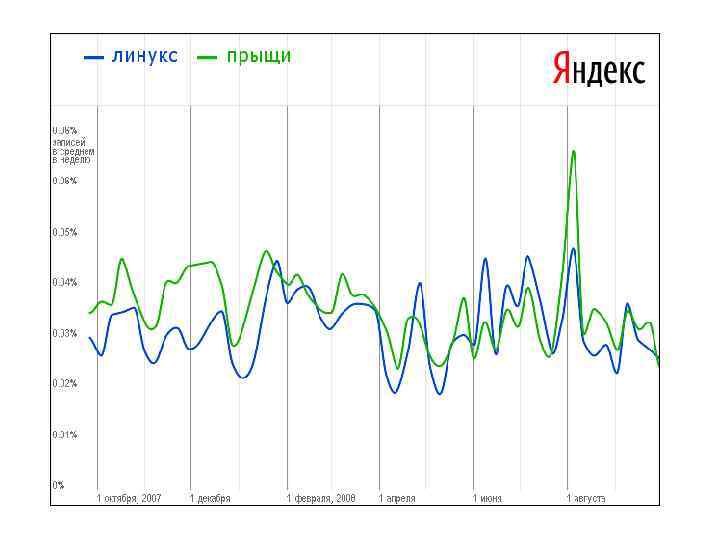
Наличие корреляций двух признаков (любой силы) не может интерпретироваться как доказательство причинно-следственной связи этих признаков. Корреляционный анализ устанавливает наличие и силу только статистической связи. Описание взаимосвязи качественных (порядковых) признаков правильнее называть ассоциацией. Если два признака по чистой случайности изменяются сходным образом, они будут коррелировать между собой. Доля объясненной дисперсии: r 2× 100 (%)

1. Корреляция, даже статистически высокозначимая, должна характеризоваться достаточным числом наблюдений (не менее 20 в каждой); 2. Устанавливать уровень значимости (α) с поправкой на множественность сравнений, т. е. он должен быть разумно низким, например, ≤ 0, 01 или даже ≤ 0, 001 – это повышает вероятность того, что корреляция не будет являться результатом случайного совпадения; 3. Каждая выявленная корреляционная зависимость должна получать четкое логическое обоснование, подтверждая некоторый известный науке феномен либо внятную, обоснованную гипотезу.

Регрессионный анализ Позволяет установить параметры функции зависимости одного признака (т. н. «зависимого» либо «объясняемого» ) от одного либо нескольких других признаков ( «независимых» , «факторов» либо «ковариат» ). Относится к методам математического моделирования. Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. Может быть: 1. Однофакторный (один независимый признак) и многофакторный (два и более независимых признаков) 2. Линейный (полиноминальная функция первой степени) и нелинейный (логит, пробит, пропорциональных рисков по Коксу, экспоненциальная регрессия и т. п. ).

Классический регрессионный анализ не предусматривает использования количественных дискретных и качественных признаков (но есть специальные модификации). Результат регрессионного анализа – построение регрессионного уравнения с наибольшим коэффициентом детерминации (R 2).

Однофакторный линейный регрессионный анализ (простая регрессия) Один из вариантов двумерного статистического анализа. 1. Число объектов исследования в несколько раз больше числа независимых признаков; 2. Все анализируемые признаки – количественные, непрерывные, нормально распределенные; 3. Каждому значению Х соответствует только одно значение Y; 4. В случае множественного регрессионного анализа – также отсутствие линейных корреляций между независимыми признаками (т. н. отсутствие мультиколлинеарности объясняющих признаков).

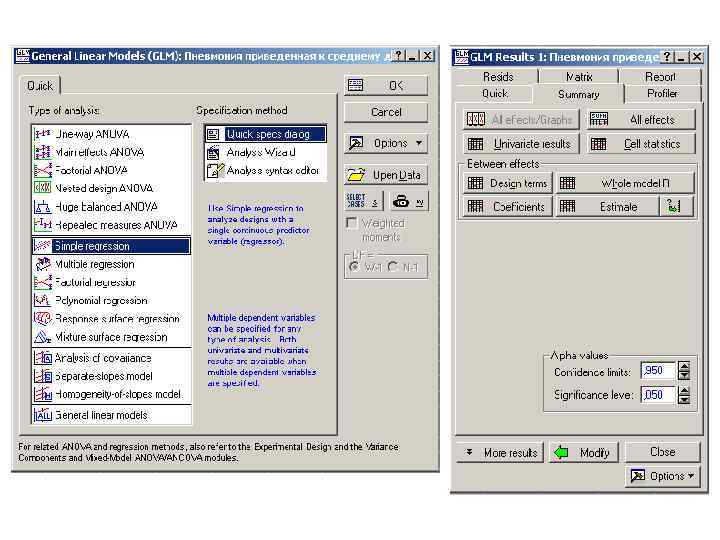
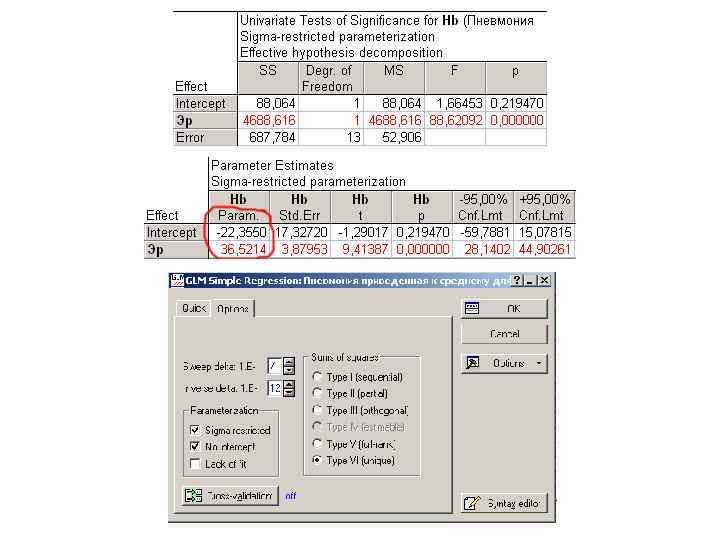
Формула простой линейной регрессии: Формула множественной линейной регрессии: В данном случае: либо

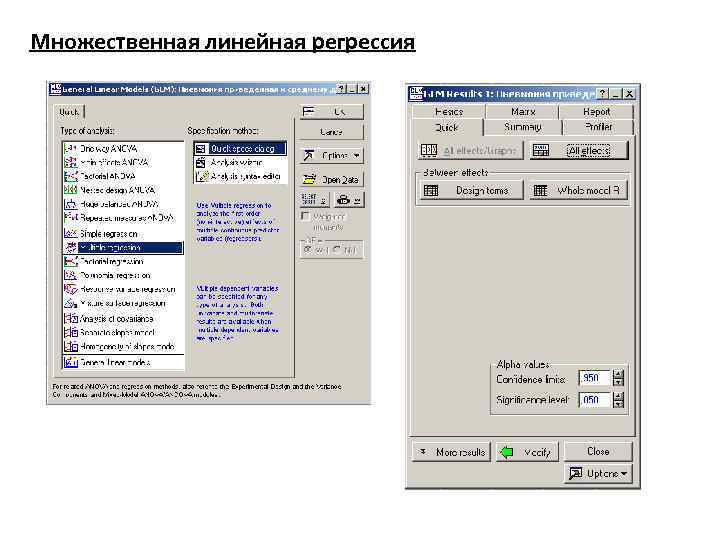Множественная линейная регрессия

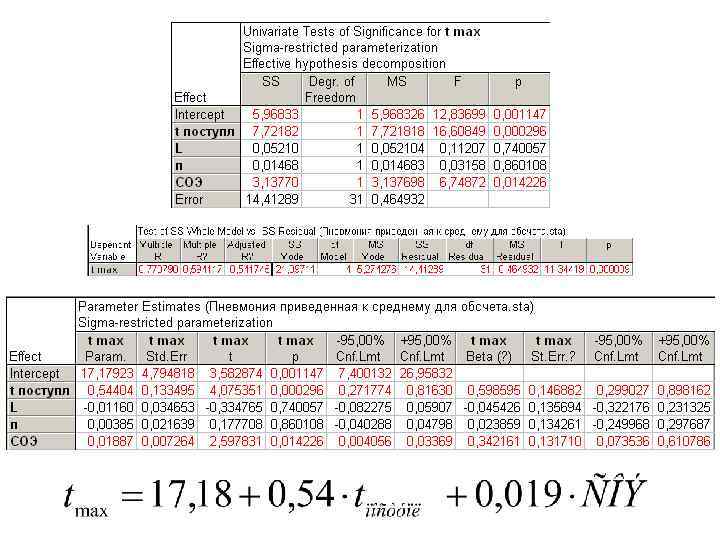
Качество построенной математической модели характеризуется показателем р (≤α), а также коэффициентом детерминации R 2 (должен максимально приближаться к единице). R 2× 100 (%) – это т. н. доля объясненной дисперсии, о которой шла речь ранее. Смысл данного понятия в том, что изменение признака Х приводит к изменению признака Y в R 2× 100 процентах случаев.

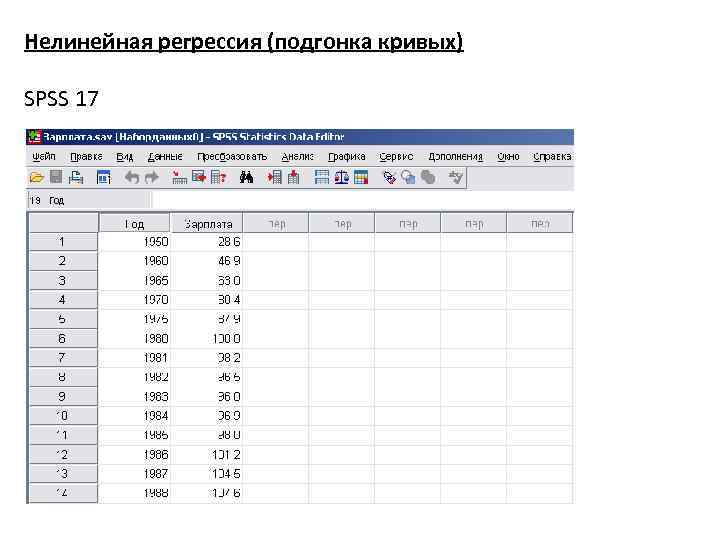Нелинейная регрессия (подгонка кривых) SPSS 17

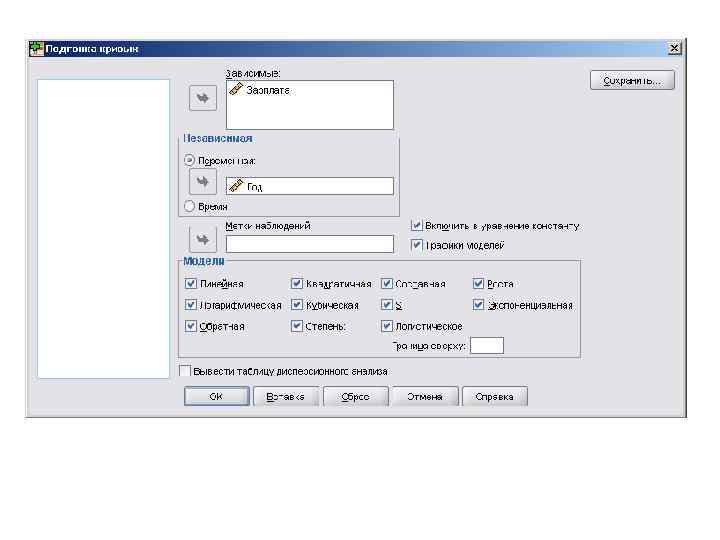
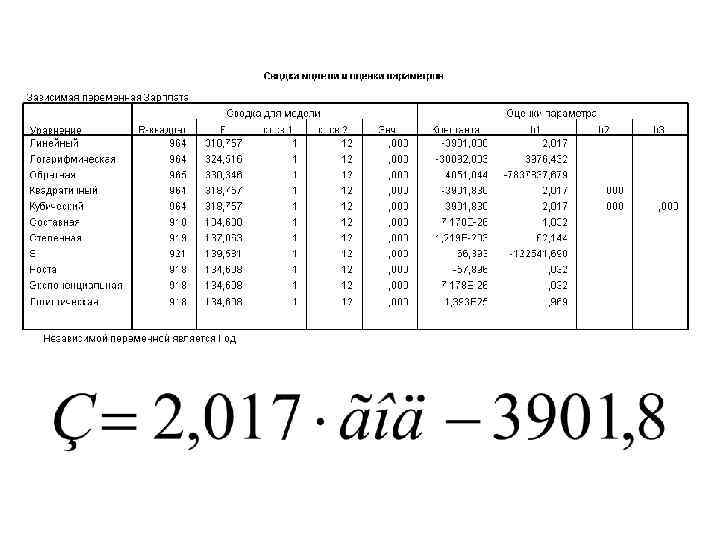
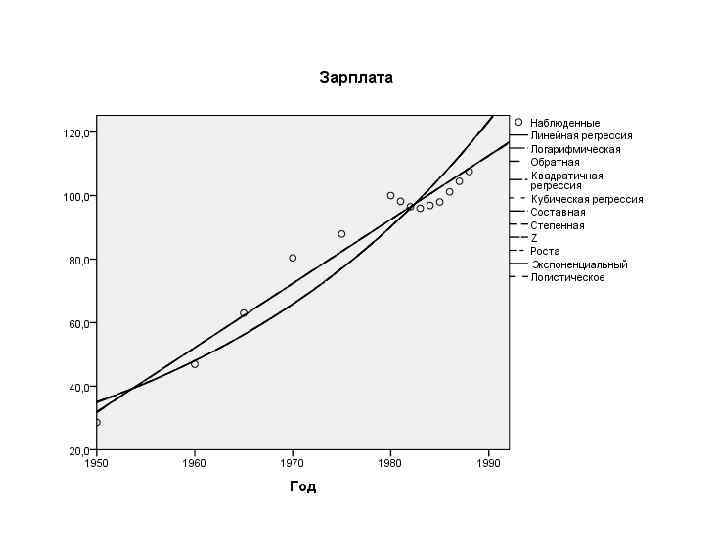
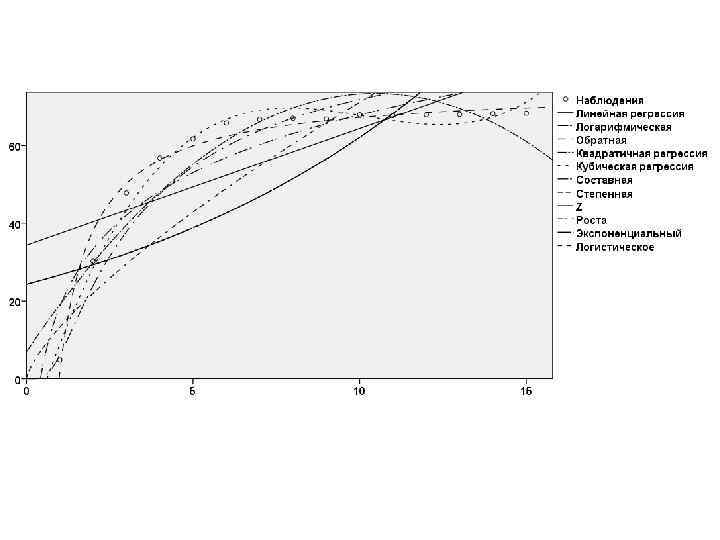
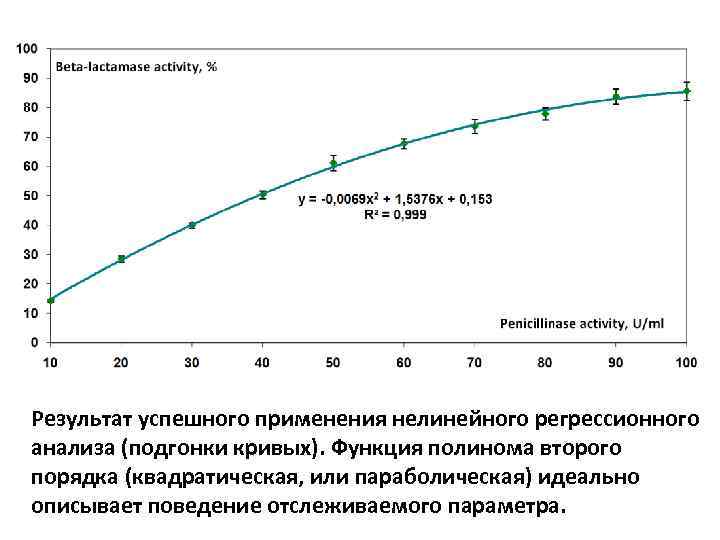Результат успешного применения нелинейного регрессионного анализа (подгонки кривых). Функция полинома второго порядка (квадратическая, или параболическая) идеально описывает поведение отслеживаемого параметра.

Цель выполнения регрессионного анализа – нахождение математической модели, наилучшим образом описывающей наблюдающуюся в эксперименте закономерность. Данная модель в дальнейшем может использоваться в медицине (например, предсказание прогноза заболевания и возможности развития его осложнений по некоторым ключевым параметрам, отслеживаемым при поступлении пациента в стационар или на ранних этапах госпитализации). Хорошие математические модели могут лечь в основу разработки анкет, опросников и шкал для диагностики различных заболеваний и определения лечебной тактики.

Признаки «хорошей» модели: Скупость (простота). Предпочтение отдается модели, содержащей меньшее число объясняющих переменных Единственность. Максимальное соответствие. Для хорошей модели значение R 2 должно составлять не менее 0, 93… 0, 95. Согласованность с теорией. Прогнозные качества.

Результаты регрессионного анализа применимы только к тому интервалу значений данных, на котором они получены. Например, если анализировалась вероятность развития заболевания по данным тестов для лиц 20 40 лет, то для лиц старше 40 и моложе 20 лет данную модель использовать некорректно.

Вне указанного интервала описанная математической моделью закономерность может (хоть и не обязана) случайным образом отличаться от таковой в пределах интервала.

Анализ взаимозависимости качественных признаков (установление взаимосвязи между воздействием и исходом) 1) Риск наступления изучаемого события (исхода) к моменту Х: Риск некоторое число в интервале между 0 и 1. 2) Шанс наступления изучаемого события (исхода) к моменту Х Шанс некоторое число между 0 и бесконечностью, приблизительно равен риску, если частота исхода невелика. Шанс с величиной N означает, что вероятность наступления исхода в N раз выше, чем того, что данный исход не наступит.

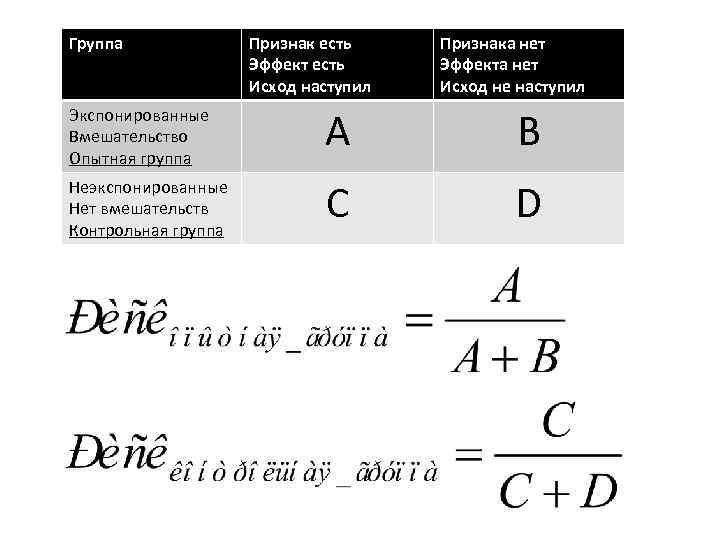Группа Признак есть Эффект есть Исход наступил Признака нет Эффекта нет Исход не наступил Экспонированные Вмешательство Опытная группа А В Неэкспонированные Нет вмешательств Контрольная группа C D

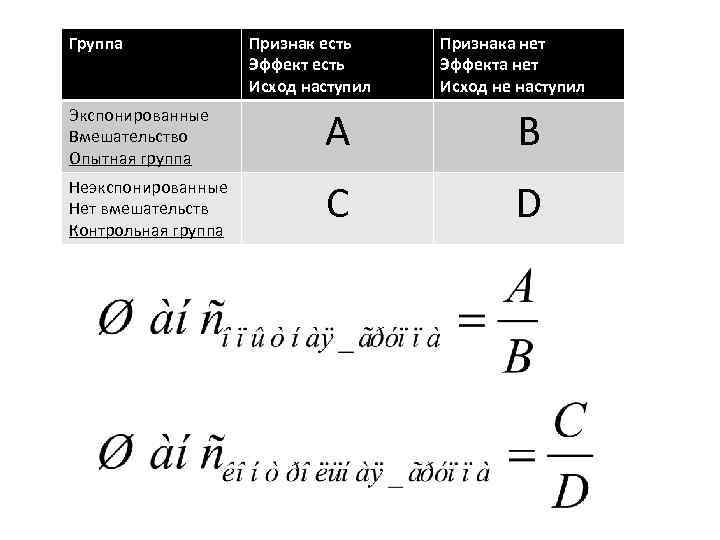Группа Признак есть Эффект есть Исход наступил Признака нет Эффекта нет Исход не наступил Экспонированные Вмешательство Опытная группа А В Неэкспонированные Нет вмешательств Контрольная группа C D

Сравнение частоты развития исхода в различных группах производится путем вычисления относительных характеристик относительного риска (relative risk, risk ratio) и отношения шансов (odds ratio).

Группа Признак есть Эффект есть Исход наступил Признака нет Эффекта нет Исход не наступил Экспонированные Вмешательство Опытная группа А В Неэкспонированные Нет вмешательств Контрольная группа C D

1. Отношение рисков либо шансов, равное 1, означает, что между опытной и контрольной группами нет разницы в вероятности либо, соответственно, шансе события; 2. Отношение рисков либо шансов, меньшее 1, означает, что в опытной группе изучаемые событие либо параметр встречаются реже, чем в контрольной; 3. Отношение рисков либо шансов, большее 1, означает, что в опытной группе изучаемые событие либо параметр встречаются чаще, чем в контрольной.

Поскольку логика научного эксперимента предполагает, что в опытной группе имело место некое исследуемое воздействие, отсутствующее в контрольной группе, RR или OR, превышающее 1, свидетельствует о наличии статистической взаимосвязи между данным воздействием и учитываемым исходом, причем воздействие увеличивает вероятность развития исхода. Соответственно, RR или OR, меньшее 1, также свидетельствует о наличии статистической взаимосвязи между воздействием (фактором) и учитываемым исходом, причем воздействие уменьшает вероятность развития исхода. В такой ситуации можно сказать, что исследуемый фактор оказывает на подопытных лиц протективное воздействие. В том случае, если RR или OR равны 1, статистическая взаимосвязь между воздействием и исходом отсутствует.

Доверительный интервал для относительного риска: 1. Вначале подсчитывают фактор ошибки относительного риска: При использовании коэффициента 1, 96 производится расчет 95% доверительного интервала. 2. Затем вычисляют верхний и нижний пределы доверительного интервала:

Доверительный интервал для отношения шансов: 1. Вначале подсчитывают фактор ошибки отношения шансов: При использовании коэффициента 1, 96 производится расчет 95% доверительного интервала. 2. Затем вычисляют верхний и нижний пределы доверительного интервала:

В том случае, если нижний предел рассчитанного доверительного интервала ≤ 1, изучаемый фактор не может быть достоверной причиной интересующего нас явления. Обратно этому, если ОШ (ОР) > 1, и при этом нижний предел ДИ также > 1, данный фактор может (но не обязан!) быть причиной изучаемого явления. Если же ОШ (ОР) < 1, и верхний предел ДИ также < 1, то изучаемый фактор оказывает протективное влияние, предотвращая появление определённого исхода. Выводы о наличии влияния изучаемого фактора на исход делаются, если вычисленные величины ОШ или ОР достаточно велики (>2 или <0, 5).

Расчет отношений шансов/рисков является простым, но одновременно и довольно грубым способом установления статистической взаимосвязи между воздействием и исходом, поскольку он не учитывает изменения объема исследуемой группы (выборки) в ходе исследования. Существуют гораздо более сложные и точные методы для выявления такой взаимосвязи и оценки ее выраженности – например, анализ дожития по Каплану Мейеру (product limit Kaplan Meier estimation).