3Логика.ppt
- Количество слайдов: 35
 Основы логики и логические основы компьютера Логика – это наука о формах и способах мышления
Основы логики и логические основы компьютера Логика – это наука о формах и способах мышления
 Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта
 Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно
 Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение)
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение)
 Алгебра высказываний В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0)
Алгебра высказываний В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0)
 Логическое умножение (конъюнкция) Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания
Логическое умножение (конъюнкция) Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания
 Операцию логического (конъюнкцию) принято значком «&» или « » F = A & B или F = A B умножения обозначать
Операцию логического (конъюнкцию) принято значком «&» или « » F = A & B или F = A B умножения обозначать
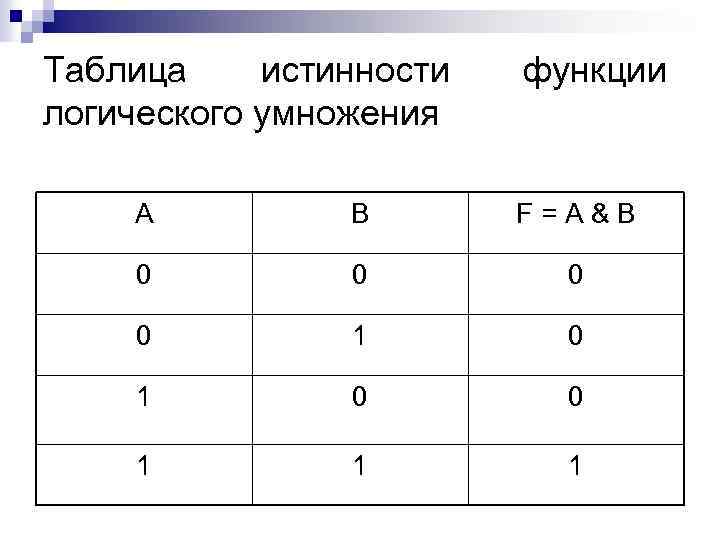 Таблица истинности логического умножения функции A B F=A&B 0 0 1 1 1
Таблица истинности логического умножения функции A B F=A&B 0 0 1 1 1
 Пример Составное высказывание: « 2*2=4 и 3*3=10» Первое высказывание истинно (А=1) Второе высказывание ложно (В=0) По таблице определяем, что логическая функция принимает значение ложь (F=0), то есть данное составное высказывание ложно
Пример Составное высказывание: « 2*2=4 и 3*3=10» Первое высказывание истинно (А=1) Второе высказывание ложно (В=0) По таблице определяем, что логическая функция принимает значение ложь (F=0), то есть данное составное высказывание ложно
 Логическое сложение (дизъюнкция) Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний
Логическое сложение (дизъюнкция) Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний
 Операцию логического (дизъюнкцию) принято значком «+» или « » F = A + B или F = A B сложения обозначать
Операцию логического (дизъюнкцию) принято значком «+» или « » F = A + B или F = A B сложения обозначать
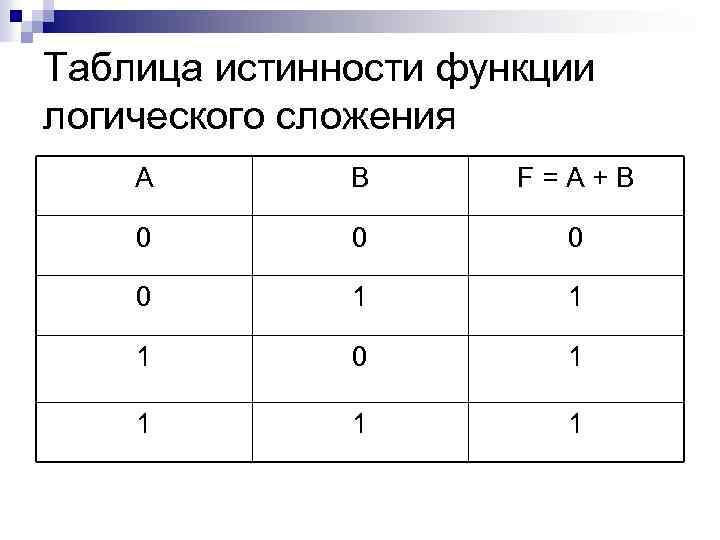 Таблица истинности функции логического сложения A B F=A+B 0 0 1 1 1 0 1 1
Таблица истинности функции логического сложения A B F=A+B 0 0 1 1 1 0 1 1
 Пример Составное высказывание: « 2*2=4 и 3*3=10» Первое высказывание истинно (А=1) Второе высказывание ложно (В=0) По таблице определяем, что логическая функция принимает значение истина (F=1), то есть данное составное высказывание истинно
Пример Составное высказывание: « 2*2=4 и 3*3=10» Первое высказывание истинно (А=1) Второе высказывание ложно (В=0) По таблице определяем, что логическая функция принимает значение истина (F=1), то есть данное составное высказывание истинно
 Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное - истинным
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное - истинным
 Операцию логического отрицания (инверсию) над логическим высказыванием А в алгебре логики принято обозначать А F=A
Операцию логического отрицания (инверсию) над логическим высказыванием А в алгебре логики принято обозначать А F=A
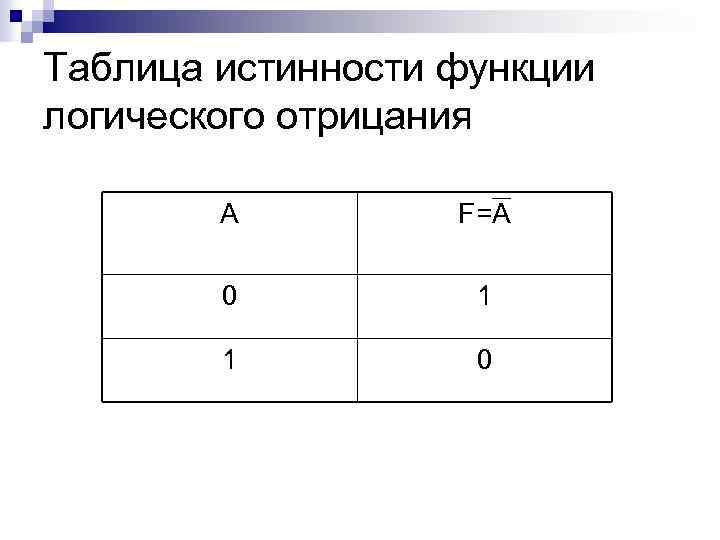 Таблица истинности функции логического отрицания A F=A 0 1 1 0
Таблица истинности функции логического отрицания A F=A 0 1 1 0
 Пример Высказывание «два умножить на два не равно четырем» ложно (А=0), а полученное из него в результате логического отрицания высказывание «два умножить на два равно четырем» истинно (F=1)
Пример Высказывание «два умножить на два не равно четырем» ложно (А=0), а полученное из него в результате логического отрицания высказывание «два умножить на два равно четырем» истинно (F=1)
 Логические выражения и таблицы истинности Составное высказывание «(2*2=5 или 2*2=4) и (2*2=5 или 2*2=4)» А = « 2*2=5» - ложно (0) В = « 2*2=4» - истинно (1) Тогда можно записать в следующей форме: «(А или В) и (А или В)» Теперь запишем в форме логического выражения: F = (A B) & (A B) = (0 1) & (1 0) = 1 & 1 = 1
Логические выражения и таблицы истинности Составное высказывание «(2*2=5 или 2*2=4) и (2*2=5 или 2*2=4)» А = « 2*2=5» - ложно (0) В = « 2*2=4» - истинно (1) Тогда можно записать в следующей форме: «(А или В) и (А или В)» Теперь запишем в форме логического выражения: F = (A B) & (A B) = (0 1) & (1 0) = 1 & 1 = 1
 Последовательность действий при построении таблиц истинности n n Определить количество строк в таблице истинности (если количество логических переменных равно n, то количество строк 2 n) Определить количество столбцов (количество логических переменных плюс количество операций) Построить таблицу и обозначить столбцы, внести в таблицу наборы значений исходных логических переменных Заполнить таблицу (выполнить базовые логические операции в необходимой последовательности)
Последовательность действий при построении таблиц истинности n n Определить количество строк в таблице истинности (если количество логических переменных равно n, то количество строк 2 n) Определить количество столбцов (количество логических переменных плюс количество операций) Построить таблицу и обозначить столбцы, внести в таблицу наборы значений исходных логических переменных Заполнить таблицу (выполнить базовые логические операции в необходимой последовательности)
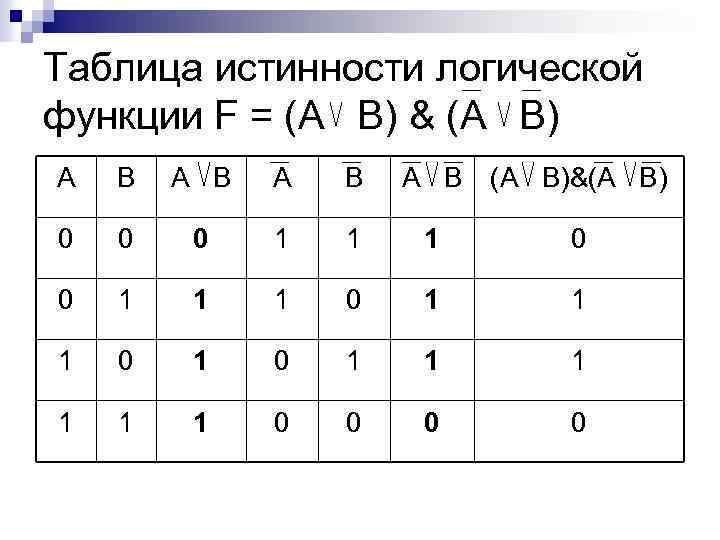 Таблица истинности логической функции F = (A B) & (A B) A B A B (A B)&(A B) 0 0 0 1 1 1 0 1 1 1 0 0
Таблица истинности логической функции F = (A B) & (A B) A B A B (A B)&(A B) 0 0 0 1 1 1 0 1 1 1 0 0
 Равносильные выражения логические Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными Для обозначения равносильных логических выражений используется знак «=»
Равносильные выражения логические Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными Для обозначения равносильных логических выражений используется знак «=»
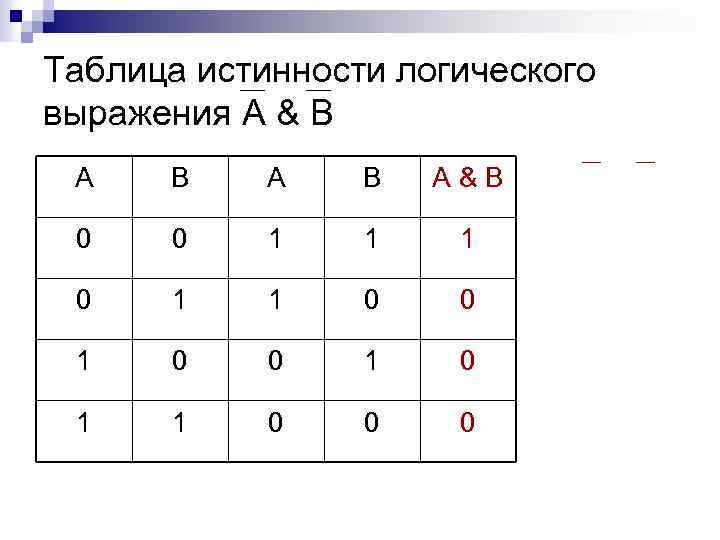 Таблица истинности логического выражения А & В А В А&В 0 0 1 1 1 0 0 1 0 1 1 0 0 0
Таблица истинности логического выражения А & В А В А&В 0 0 1 1 1 0 0 1 0 1 1 0 0 0
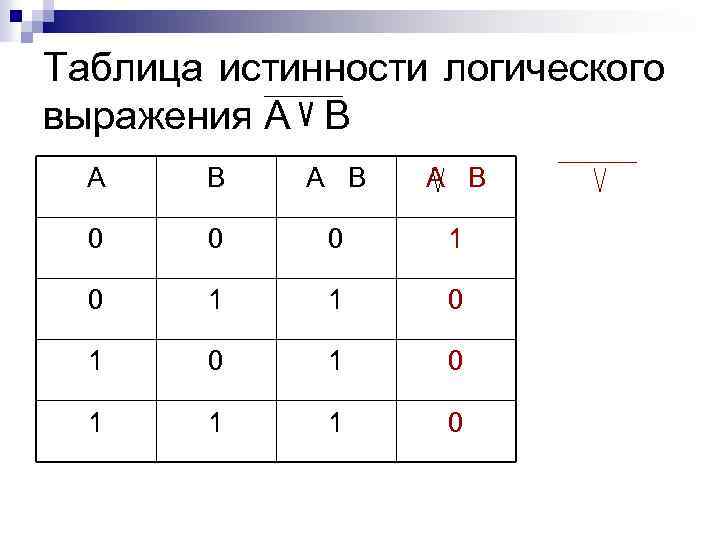 Таблица истинности логического выражения А В А В 0 0 0 1 1 0 1 0 1 1 1 0
Таблица истинности логического выражения А В А В 0 0 0 1 1 0 1 0 1 1 1 0
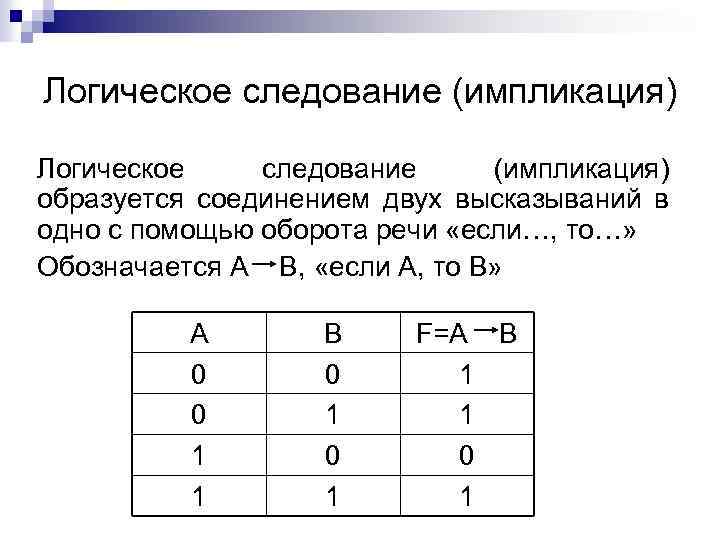 Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…» Обозначается А В, «если А, то В» А 0 0 1 1 В 0 1 F=A B 1 1 0 1
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…» Обозначается А В, «если А, то В» А 0 0 1 1 В 0 1 F=A B 1 1 0 1
 Составное высказывание образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания)следует ложный вывод (второе высказывание)
Составное высказывание образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания)следует ложный вывод (второе высказывание)
 Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда…» Обозначается А ~ В А 0 0 1 1 В 0 1 А~В 1 0 0 1
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда…» Обозначается А ~ В А 0 0 1 1 В 0 1 А~В 1 0 0 1
 Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны
 Закон тождества Всякое высказывание самому себе А=А тождественно
Закон тождества Всякое высказывание самому себе А=А тождественно
 Закон непротиворечия Высказывание не может быть одновременно истинным и ложным. Если высказывание истинно, то его отрицание должно быть ложно. Логическое произведение высказывания и его отрицания должно быть ложно А&A=0
Закон непротиворечия Высказывание не может быть одновременно истинным и ложным. Если высказывание истинно, то его отрицание должно быть ложно. Логическое произведение высказывания и его отрицания должно быть ложно А&A=0
 Закон исключенного третьего Высказывание может быть либо истинным, либо ложным, третьего не дано А А=1
Закон исключенного третьего Высказывание может быть либо истинным, либо ложным, третьего не дано А А=1
 Закон двойного отрицания Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание А=А
Закон двойного отрицания Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание А=А
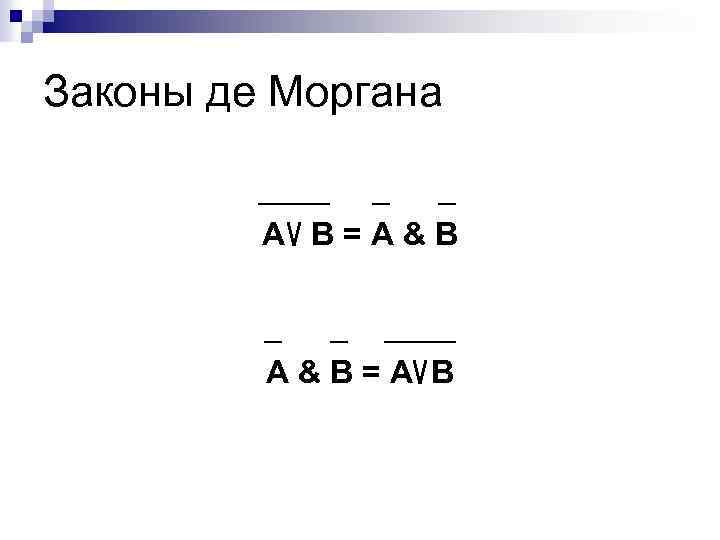 Законы де Моргана А В=А&В А&В=А В
Законы де Моргана А В=А&В А&В=А В
 Закон коммутативности Можно менять местами логические переменные при операциях логического умножения и логического сложения: А & B = B & A (логическое умножение) A B=B A (логическое сложение)
Закон коммутативности Можно менять местами логические переменные при операциях логического умножения и логического сложения: А & B = B & A (логическое умножение) A B=B A (логическое сложение)
 Закон ассоциативности Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебречь скобками или произвольно их расставлять (A & B) & C = A & (B & C) (A B) C = A (B C)
Закон ассоциативности Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебречь скобками или произвольно их расставлять (A & B) & C = A & (B & C) (A B) C = A (B C)
 Закон дистрибутивности В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые (A & B) (A & C) = A & (B C) (A B) & (A C) = A (B & C)
Закон дистрибутивности В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые (A & B) (A & C) = A & (B C) (A B) & (A C) = A (B & C)


