ОСНОВЫ ЛОГИКИ Формальная логика отделяет содержание процесса

ОСНОВЫ ЛОГИКИ

Формальная логика отделяет содержание процесса мышления от его общих принципов. Это означает, например, если вы обещаете прибыть на встречу, то для логики важно прибудете или нет, а на каком виде транспорта и в какой одежде для нее не имеет значения. Или, когда вы говорите: я выпью кофе, если он будет крепким, сладким и горячим, для логики не имеет значения, кто, как, когда и каким способом будет готовить условия для логичного завершения действия.

Логика изучает структуру процесса мышления. Мышление это сложный процесс, но и его можно разложить на некоторое количество форм (то, при помощи чего мы выражаем свои мысли), которые объединяются по общим признакам. Итак, мышление может быть выражено следующими формами. 1. Понятие 2. Суждение (высказывание). 3. Умозаключение 4. Доказательство.

Понятие – форма мышления, отражающая существенные формы предмета или явления. (Яркий свет, круглый камень, холодная погода). Высказывание это форма мышления, выраженная при помощи понятий, когда что-то утверждается или отрицается. - Монета упала изображением номинала (решкой) вверх. - Спортсмен преодолел планку на высоте 2. 20. - Из-за обрыва провода не воспроизводится звук в наушниках MP 3 плейера. - Я еду с требуемой скоростью при виде знака по ее ограничению. Высказывание существует в двух формах – ИСТИНА и ЛОЖЬ Суждение истинно, если оно правильно отражает свойства или отношения реальных вещей. Суждение ложно, если оно искажает объективные отношения.

Фундаментальное понятие логики – она не рассматривает обоснование истинности. В естественном языке высказывание – повествовательное предложение. Высказывания используют формальные языки – математика, физика, химия. Электронные устройства, в том числе и компьютерные тоже могут обмениваться высказываниями (сообщениями), которые, тоже могут подчиняться законам логики. Высказывание считается простым, если никакая из его частей не является высказыванием.

Логические функции. Основная задача - логики рассмотрение сложных логических выражений. Простые высказывания соединяются в сложные при помощи логических связок (функций). Логическая функция это формальное правило преобразования или объединения высказываний, пришедшее в логику из обычной жизни.

Основные логические функции: Инверсия – НЕ Функция преобразующая исходное высказывание в обратное. - Приятель будет звонить мне в 17. 00. (А он не позвонил) - Кран сможет поднять груз на эту высоту. (А он не смог) Дизъюнкция – ИЛИ логическое сложение. - Ты должен помыть посуду или убраться в комнате, тогда пойдешь гулять. (Необходимо выполнить или то, в этом случае результатом будет истина и вы пойдете гулять) Конъюнкция – И логическое умножение. - Вы должны владеть иностранным языком и иметь высшее образование, только тогда вас возьмут на работу. (Наличие одного из условий не обеспечивает вашего приема на работу. Только в случае если и первое и второе выполняется тогда результатом станет истина - прием на работу) Импликация – следование. (Импликация не имеет простой жизненной интерпретации). Для себя я ее определяю по следующему правилу. Трагедия в том, что хотел, но не получилось. В результате: Хотел и получилось - это истина. Не хотел, а получилось, тоже истина. Не хотел и не получилось истина потому, что мне нет до этого никакого дела. Эквиваленция – равенство. Здесь все просто - результат - истина если исходные высказывания эквивалентны: оба истины или ложны.

Таблица обозначений логических связок - функций Логическая связка (функция) Обозначение A и B A & B, A and B, A Λ B Конъюнкция A или B A V B, A or B Дизъюнкция Не А , A неверно _ ¬ A, A Инверсия Из A следует B, Если A то B, A влечет B, B следствие A A -> B, If A then B Импликация Следование A равно B A <--> B Эквиваленция Название

Принято ложь определять как 0, а истину, как 1.

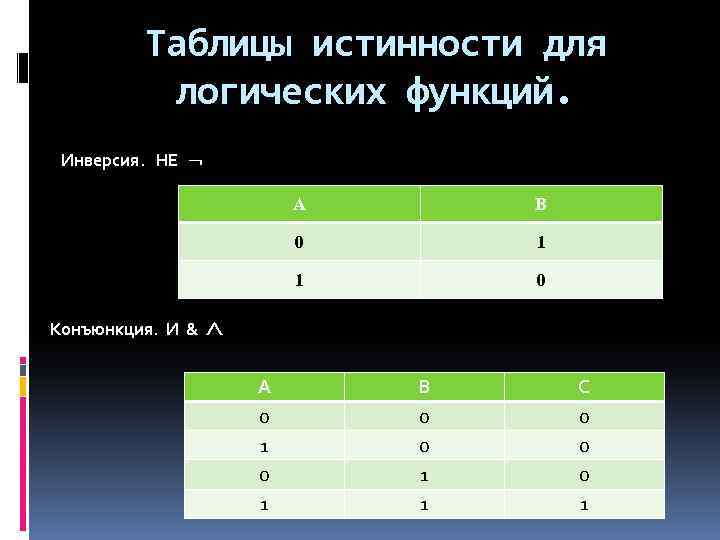Таблицы истинности для логических функций. Инверсия. НЕ A B 0 1 1 0 Конъюнкция. И & A 0 1 B 0 0 1 1 C 0 0 0 1

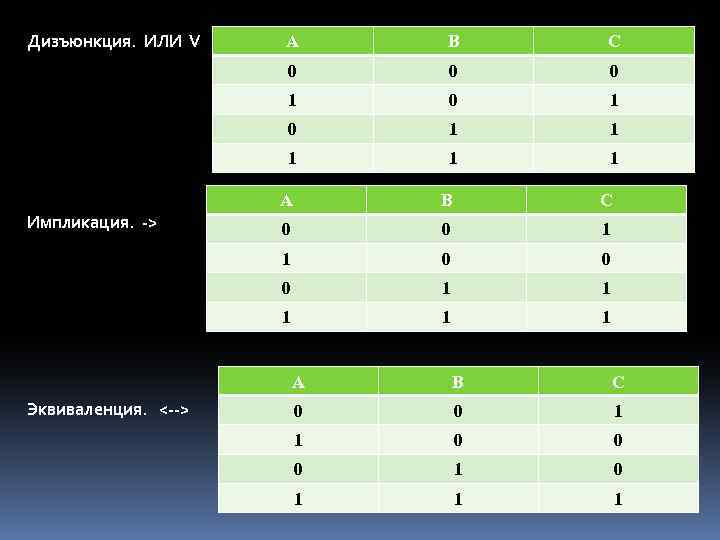Дизъюнкция. ИЛИ V B C 0 0 0 1 0 1 1 1 A B C 0 0 1 1 0 0 0 1 1 1 Импликация. -> A 1 1 A Эквиваленция. <--> B C 0 0 1 1 0 0 0 1 1 1

Построение (запись) логических выражений. Каждое сложное (составное) высказывание можно выразить в виде формулы – логического выражения. В выражение входят: - логические переменные, которые обозначают высказывания - знаки логических операций, которые обозначают логические функции. Для составления выражений на языке алгебры логики нужно выделить простые высказывания и логические связки между ними.

Пример (X * Y = 5 или X * Y = 4 ) И (X * Y ≠ 5 или X * Y ≠ 4) Подставим в выражение значения x=2, y=2 (2 * 2 = 5 или 2 * 2 = 4) И (2 * 2 ≠ 5 или 2 * 2 ≠ 4) Выделяем простые высказывания и связки ( A или B ) И (¬A или ¬B ) Запишем выражение логической функции F = ( A V B ) & (¬A V ¬B ) Подставим в функцию формальные значения высказываний. F = ( 0 V 1) & (1 V 0) = 1 & 1 = 1 - для данных условий результирующим значением функции является истина

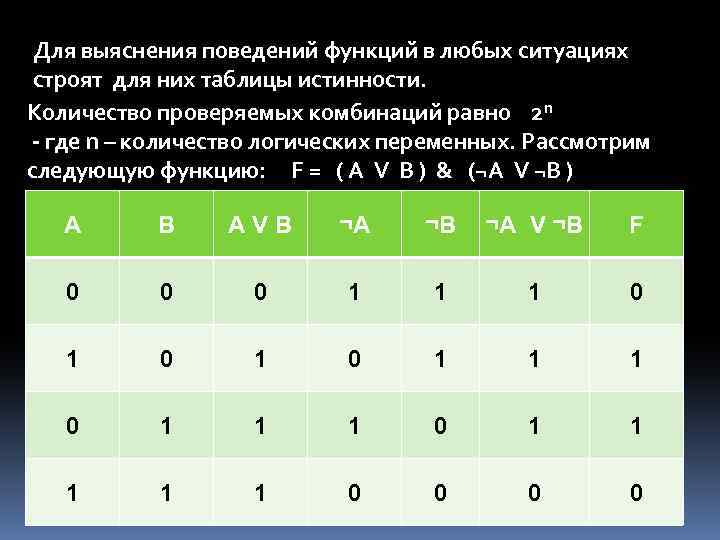Для выяснения поведений функций в любых ситуациях строят для них таблицы истинности. Количество проверяемых комбинаций равно 2 n - где n – количество логических переменных. Рассмотрим следующую функцию: F = ( A V B ) & (¬A V ¬B ) А B A V B ¬A ¬B ¬A V ¬B F 0 0 0 1 1 1 0 1 1 1 0 0

Двойного отрицания А = ¬(¬A) Переместительный (коммутативный) A V B = B V A A & B = B & A Сочетательный (ассоциативный) (A V B) V C = A V (B V C) (A&B) & C = A & (B & C) Распределительный (дистрибутивный) (A V B) & C = (A & C) V (B & C) (A & B) V C = (A V C) & (B V C) Закон общ. инверсии (законы де Моргана) ¬( A V B) = ¬A & ¬B ¬(A & B) = ¬A V ¬B Закон идемпотентности A V A = A A & A = A Законы исключения констант A V 1 = 1, A V 0 = A A & 1 = A, A & 0 = 0 Закон противоречия A V ¬A = 1. A & ¬A= 0. Закон поглощения A V (A & B) = A A & (A V B) = A Закон исключения (склеивания): (A&B) V (¬A & B) = B (A V B) & (¬A V B) = B

Использование законов логики позволяет равносильно преобразовывать логические выражения, что зачастую приводит к их упрощению. А V (┐А & В) = (A V ┐А) & (AV B) = 1 & (AV B) = (1 &A) V (1 &B) = A V B А V (┐А & В) = A V B

(А V В) & (┐A V B) & (С V┐B ) = B & (С V┐B ) = (B&С) V (B &┐B) = (B&┐С) V 0 = (B V 0) & (C V 0) = B & C ┐((A v B) → ┐(B v C)) = A v B & ┐ ┐(B v C) = (A v B) & (B v C) = B v (A & C)