Основы квантовой волновой механики Законы классической механики применимы

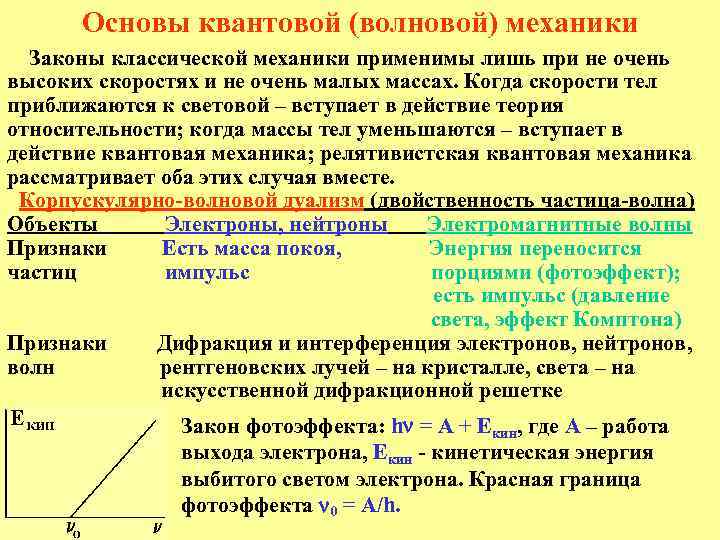Основы квантовой (волновой) механики Законы классической механики применимы лишь при не очень высоких скоростях и не очень малых массах. Когда скорости тел приближаются к световой – вступает в действие теория относительности; когда массы тел уменьшаются – вступает в действие квантовая механика; релятивистская квантовая механика рассматривает оба этих случая вместе. Корпускулярно-волновой дуализм (двойственность частица-волна) Объекты Электроны, нейтроны Электромагнитные волны Признаки Есть масса покоя, Энергия переносится частиц импульс порциями (фотоэффект); есть импульс (давление света, эффект Комптона) Признаки Дифракция и интерференция электронов, нейтронов, волн рентгеновских лучей – на кристалле, света – на искусственной дифракционной решетке Закон фотоэффекта: h = A + Eкин, где А – работа выхода электрона, Eкин - кинетическая энергия выбитого светом электрона. Красная граница фотоэффекта 0 = А/h.

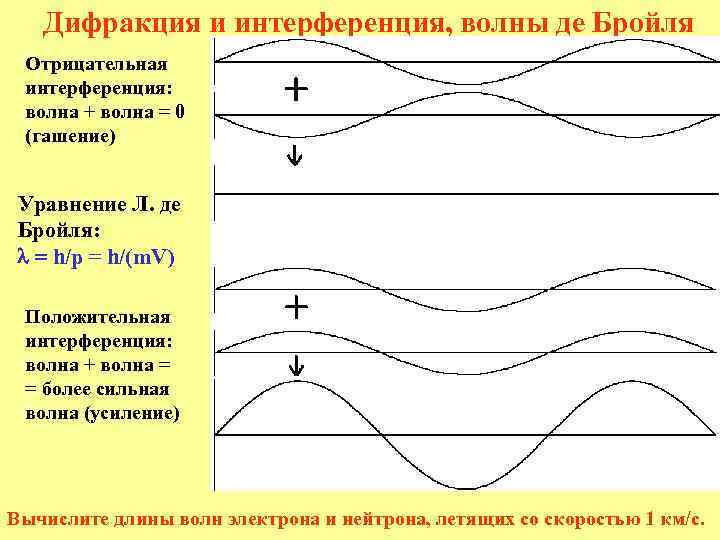Дифракция и интерференция, волны де Бройля Отрицательная интерференция: волна + волна = 0 (гашение) Уравнение Л. де Бройля: l = h/p = h/(m. V) Положительная интерференция: волна + волна = = более сильная волна (усиление) Вычислите длины волн электрона и нейтрона, летящих со скоростью 1 км/c.

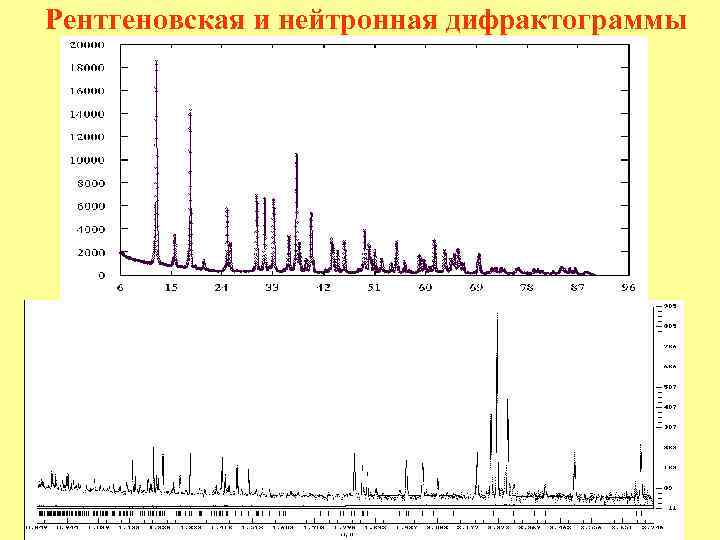Рентгеновская и нейтронная дифрактограммы

Принцип неопределенности Гейзенберга и его философское значение Волновые свойства частиц приводят к тому, что становится невозможно определить одновременно положение и скорость (или импульс) частицы: чем точнее измеряем скорость, тем менее определенным является положение частицы и наоборот. Количественное выражение этого дает соотношение неопределенностей В. Гейзенберга: x* px h/2 p, где x – погрешность определения координаты х, px – погрешность определения проекции импульса на ось х (и то же для осей y и z). Импульс p=m. V. Постоянная Планка так мала, что для макроскопических тел указанные погрешности совершенно незаметны. Но для микрочастиц они очень существенны. Всякое измерение влияет на измеряемый объект !!!

Волновая функция и волновое уравнение Если электрон – волна, то его поведение должно описываться волновой функцией Y, которую можно найти, решив соответствующее дифференциальное уравнение, подобно тому, как колебания струны описываются синусоидальной функцией, получающейся при решении дифференциального уравнения для гармонических колебаний. Y – функция координат и времени: x, y, z, t или r, q, f, t. Сама Y не имеет ясного физического смысла, но ее квадрат (точнее, квадрат ее модуля |Y|2, т. к. Y может быть комплексной величиной) пропорционален плотности вероятности пребывания электрона в данной точке пространства. Если V – объем, а w – вероятность пребывания электрона в этом объеме, то w/V – плотность вероятности. В точке - dw/d. V. |Y|2 = dw/d. V Мы не будем решать волновое уравнение (уравнение Шрёдингера) и даже записывать готовые волновые функции, а рассмотрим важные для химии результаты. У Карапетьянца решения записаны неверно! Правильно – у Коттона и Уилкинсона.

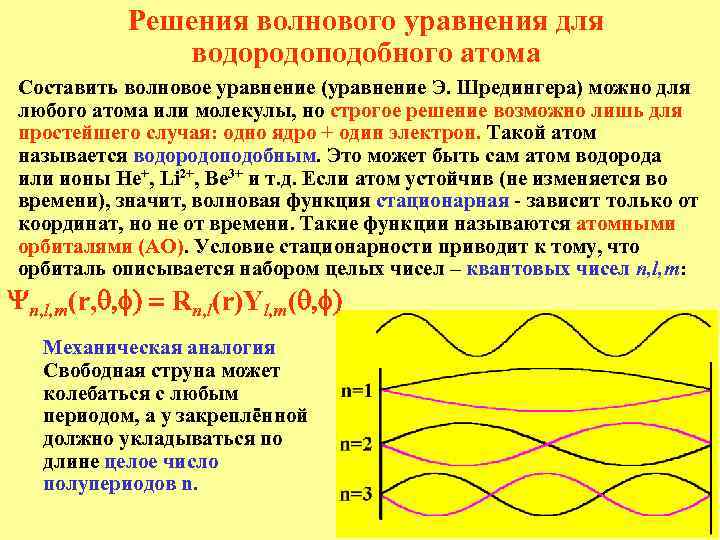Решения волнового уравнения для водородоподобного атома Составить волновое уравнение (уравнение Э. Шредингера) можно для любого атома или молекулы, но строгое решение возможно лишь для простейшего случая: одно ядро + один электрон. Такой атом называется водородоподобным. Это может быть сам атом водорода или ионы He+, Li 2+, Be 3+ и т. д. Если атом устойчив (не изменяется во времени), значит, волновая функция стационарная - зависит только от координат, но не от времени. Такие функции называются атомными орбиталями (АО). Условие стационарности приводит к тому, что орбиталь описывается набором целых чисел – квантовых чисел n, l, m: Yn, l, m(r, q, f) = Rn, l(r)Yl, m(q, f) Механическая аналогия Свободная струна может колебаться с любым периодом, а у закреплённой должно укладываться по длине целое число полупериодов n.

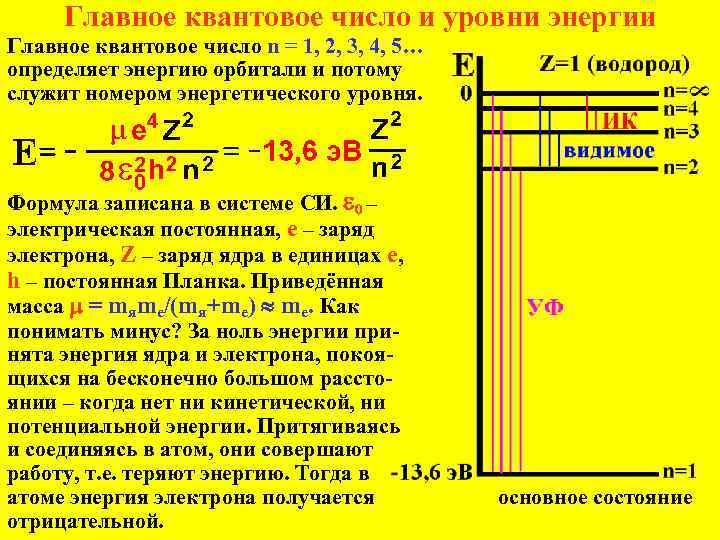Главное квантовое число и уровни энергии Главное квантовое число n = 1, 2, 3, 4, 5… определяет энергию орбитали и потому служит номером энергетического уровня. Формула записана в системе СИ. e 0 – электрическая постоянная, е – заряд электрона, Z – заряд ядра в единицах е, h – постоянная Планка. Приведённая масса = mяme/(mя+me) mе. Как понимать минус? За ноль энергии принята энергия ядра и электрона, покоящихся на бесконечно большом расстоянии – когда нет ни кинетической, ни потенциальной энергии. Притягиваясь и соединяясь в атом, они совершают работу, т. е. теряют энергию. Тогда в атоме энергия электрона получается отрицательной. основное состояние

Атомные спектры Если атомарный водород возбудить, т. е. перевести электрон с первого уровня на более высокий, сообщив ему энергию (например, соударениями атомов при высокой температуре в электрической дуге), то он довольно быстро переходит в состояние с более низкой энергией, теряя энергию в виде электромагнитного кванта. Поскольку уровни энергии строго определённые, то и разности их энергий – тоже, и испускаемое излучение имеет строго определённые частоты и длины волн, а промежуточных не может быть: Спектр испускания водорода У многоэлектронных атомов спектры сложнее, но тоже линейчатые: Спектр испускания натрия Непрерывный спектр Спектр поглощения содержит провалы (чёрные линии) там же, где были яркие линии испускания: поглощаются только кванты этих частот

Другие квантовые числа и обозначения орбиталей Орбитальное квантовое число l = 0, 1, 2, 3 … n-1 Буквенные обозначения s, p, d, f … Число орбиталей на подуровне 1 3 5 7 l определяет симметрию орбитали, т. е. форму облака электронной плотности и величину орбитального момента импульса М= Vr=[l(l+1)]1/2 h/2 p. Магнитное квантовое число ml = -l… 0…+l определяет ориентацию облака в пространстве, т. е. величину проекции орбитального момента на некое выделенное направление (например, направление внешнего электрического поля). Без поля состояния с одинаковыми n и l, но разными ml эквивалентны и образуют один энергетический подуровень, а в поле их энергия становится разной – подуровень расщепляется. Например: 3 s : n = 3, l = 0, ml = 0; 3 px : n = 3, l = 1, ml = -1; 3 py : n = 3, l = 1, ml = 1; 3 pz : n = 3, l = 1, ml = 0; 3 d : n = 3, l = 2, ml = -2, -1, 0, 1, 2. Таким образом, энергия электрона, момент импульса и его ориентация квантованы, т. е. могут принимать значения только из строго определённого набора, а промежуточные значения невозможны.

Угловое распределение электронной плотности Разделение переменных позволяет рассматривать отдельно радиальную часть волновой функции Rn, l(r) и угловую Yl, m(q, f). Yn, l, m(r, q, f) = Rn, l(r)Yl, m(q, f) Угловая часть не зависит от n, поэтому все орбитали, обозначаемые одной буквой (s, p, d или f), имеют одинаковую форму. У s-орбиталей угловая часть – константа, т. е. не зависит от углов, поэтому они сферически симметричны – по всем направлениям электронная плотность одинакова. Три p-орбитали вытянуты вдоль трёх взаимно перпендикулярных осей. На рисунке – одна из них (px). График угловой p-функции – две сферы, касающиеся в центре атома – в ядре. Длина радиус-вектора r пропорциональна величине волновой функции в данном направлении. Она максимальна вдоль x и равна нулю в плоскости y 0 z. Поверхности, где электронная плотность равна нулю, называются узловыми. Плюс и минус – знаки волновой функции. Соответственно, у py -орбитали узловая поверхность x 0 z…

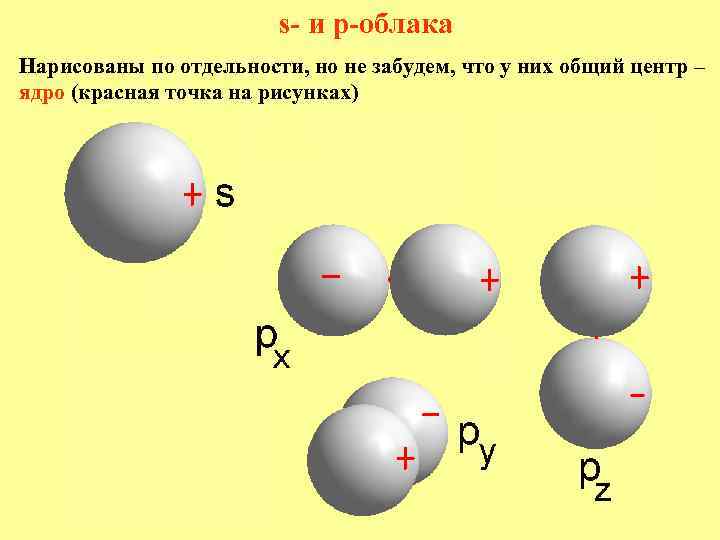s- и p-облака Нарисованы по отдельности, но не забудем, что у них общий центр – ядро (красная точка на рисунках)

Радиальное распределение электронной плотности Рассмотрим шаровой слой бесконечно малой толщины dr на расстоянии r от ядра. Его площадь 4 pr 2, а объём 4 pr 2 dr. Поскольку плотность вероятности равна Y 2, вероятность найти электрон в этом объёме dw = 4 pr 2 Y 2 dr, а плотность вероятности нахождения электрона на расстоянии r от ядра dw/dr = 4 pr 2 Y 2. Это – функция радиального распределения электронной плотности, без анализа которой трудно понять свойства атомов. Вместо Y достаточно подставить её радиальную часть. Графики на следующем слайде. Основные выводы: - у электрона нет определённой орбиты; при удалении от ядра электронная плотность асимптотически стремится к нулю, но строго в ноль не обращается, поэтому «размер атома» - понятие нестрогое; - число максимумов равно n-l; - если n-l = 1 (1 s, 2 p, 3 d, 4 f – орбитали), то единственный максимум находится на расстоянии rнаивер = n 2 a 0/Z, где «боровский радиус» 1 Å (ангстрем) = 10 -10 м

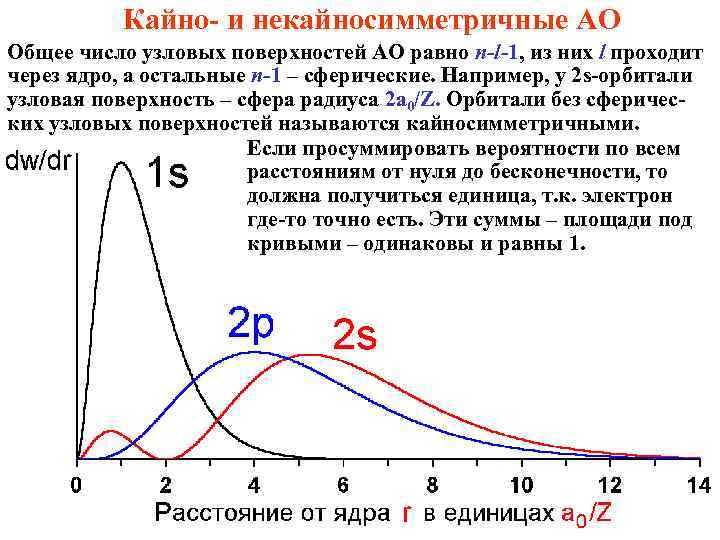Кайно- и некайносимметричные АО Общее число узловых поверхностей АО равно n-l-1, из них l проходит через ядро, а остальные n-1 – сферические. Например, у 2 s-орбитали узловая поверхность – сфера радиуса 2 a 0/Z. Орбитали без сферических узловых поверхностей называются кайносимметричными. Если просуммировать вероятности по всем расстояниям от нуля до бесконечности, то должна получиться единица, т. к. электрон где-то точно есть. Эти суммы – площади под кривыми – одинаковы и равны 1.