ОСНОВЫ КРИСТАЛЛОГРАФИИ ГЕОМЕТРИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ Кристаллография

ОСНОВЫ КРИСТАЛЛОГРАФИИ

ГЕОМЕТРИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ • Кристаллография – наука о кристаллах, их внешней форме, внутреннем строении, физических свойствах, о процессах их образования в земной коре, космосе и закономерностях развития Земли в целом. • У любого материального объекта существуют различные симметрийные уровни структурной организации. Минерал, как природный объект, не исключение, а наоборот, он является одним из главных материальных объектов земной коры, обладающий всеми свойствами кристаллического вещества, на примере которого были изучены и выведены все основные законы симметрии кристалловмногогранников. • Кристаллами называются твёрдые тела с упорядоченным внутренним строением, обладающие трёхмерно-периодической пространственной атомной структурой и имеющие вследствие этого, при определённых условиях образования, форму многогранников.

КРИСТАЛЛОГРАФИЯ Дисциплина фундаментального характера, обязательная для студентов всех естественных специальностей (физиков, химиков, геологов). 1. 2. 3. Основная литература Егоров-Тисменко Е. М. Кристаллография и кристаллохимия. М. : Изд-во МГУ, 2006. 460 с. М. П. Шаскольская. Кристаллография. М. : Высшая школа, 1976. 391 с. Г. М. Попов, И. И. Шафрановский. Кристаллография. М. : Высшая школа, 1972. 346 с.

Кристаллография как наука • Кристаллография – наука о кристаллах и кристаллическом состоянии материи вообще. • Слово «кристалл» греческого происхождения и означает «лед» , «горный хрусталь» . • Кристаллография изучает свойства кристаллов, их строение, рост и растворение, применение, искусственное получение и т. д. • Кристаллами называют твердые тела, в которых материальные частицы расположены закономерно в виде узлов пространственной решетки

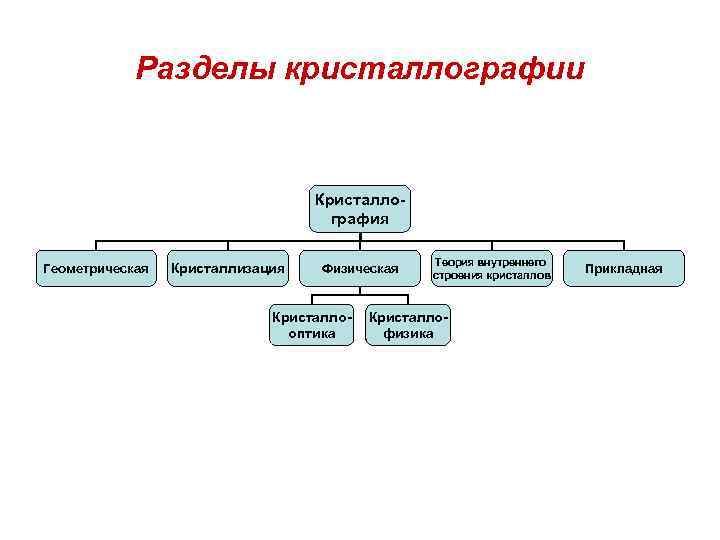Разделы кристаллографии Кристаллография Геометрическая Кристаллизация Физическая Кристаллооптика Теория внутреннего строения кристаллов Кристаллофизика Прикладная

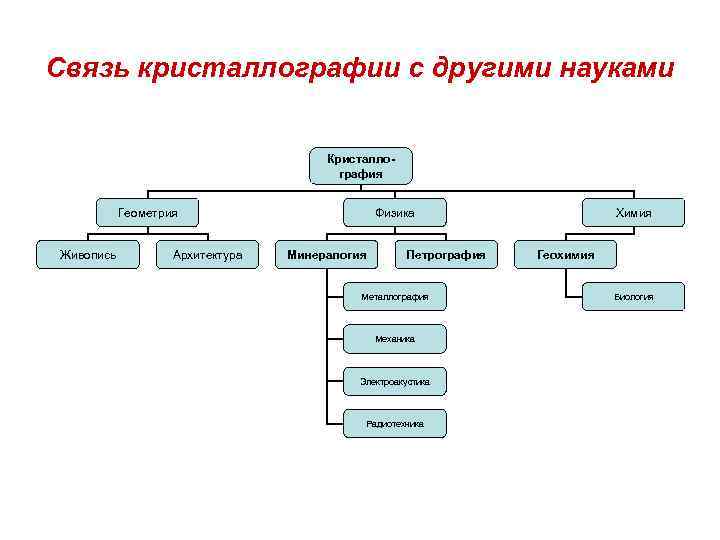Связь кристаллографии с другими науками Кристаллография Геометрия Живопись Архитектура Физика Минералогия Петрография Металлография Механика Электроакустика Радиотехника Химия Геохимия Биология

Значение кристаллографии • Теоретическое значение – познание наиболее общих закономерностей строения материи, в частности земной коры • Практическое значение – промышленное выращивание кристаллов (монокристалльная промышленность)

Понятие о структуре кристаллов • Под структурой кристаллов понимается закономерное расположение материальных частиц ( атомов, молекул, ионов ) внутри кристаллохимического вещества. • Для описания порядка расположения частиц в пространстве их начали отождествлять с точками. Из такого подхода постепенно сформировалось представление о пространственной или кристаллической решетке кристаллов минералов. • Ломоносов, Гаюи, Браве, Федоров заложили основы геометрической теории строения кристаллов. • Пространственная решетка – это бесконечное трёхмерное периодическое образование, элементами которого являются узлы, ряды, плоские сетки, элементарные ячейки. • Главная особенность кристаллохимических структур – закономерная повторяемость в пространстве узлов, рядов и плоских сеток.

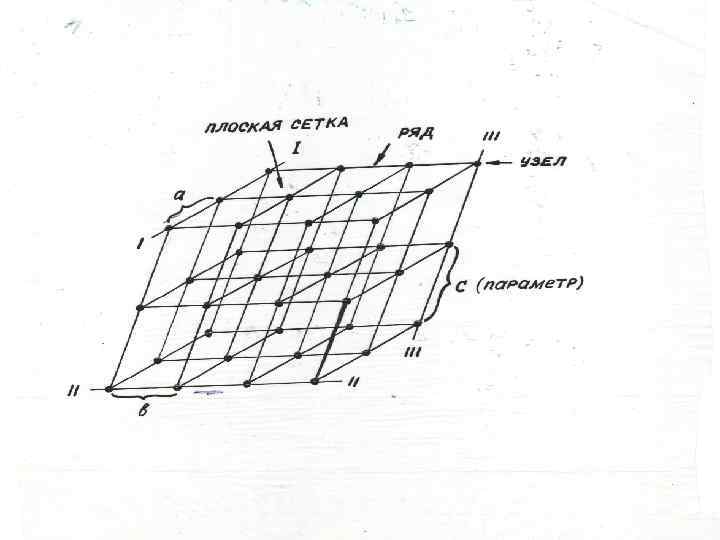
• Узлы пространственной решетки называется точки, в которых располагаются материальные частицы кристаллического вешества – атомы, ионы, молекулы, радикалы. • Ряды пространственной решетки – совокупность узлов лежащих вдоль прямой и периодически повторяющиеся через равные промежутки • Плоская сетка пространственной решетки – совокупность узлов, расположенных в одной плоскости и находящиеся в вершинах равных параллелограммов, ориентированных параллельно и сложные по целым сторонам. • Элементарная ячейка пространственной решетки – называется минимальный по объему параллелипипед образованный системой 3 -х взаимопересекающихся плоских сеток.

14 типов решеток Бравэ • В 1855 г. О. Бравэ вывел 14 пространственных решеток, рознящихся по формам элементарных ячеек и симметрии. Они представляют из себя закономерное повторение узлов пространственной решетки. Эти 14 решеток группируются по сингониям • Любая пространственная решетка может быть представлена в виде параллелипипедов повторяемости, которые перемещаясь в пространстве в направлении его ребер и на их величину формируют бесконечную пространственную решетку. • Параллелипипеды повторяемости ( элементарные ячейки решеток Бравэ ) выбирая по следующим условиям: • 1. сингония выбранного параллелипипеда • 2. число равных ребер и углов между ребрами параллелипипеда должны быть максимальными • 3. при наличии прямых углов между ребрами параллелипипеда их число должно быть наибольшим • 4. при соблюдении первых 3 -х условий объем параллелипипеда должны быть наименьшим. • При выборе элементарной ячейки пользуются уже известными правилами установки кристаллов; • Ребра ячейки – это кратчайшее расстояние вдоль координатных осей между углами решетки. • Для характеристики внешней формы элементарной ячейки используются величины ребер ячейки а, в, с и углы между этими

• Кубическая – форма элементарной ячейки соответствует кубу. • Гексагональная – гексагональная призма с пинакоидом. • Тригональная – ромбоэдр. • Тетрагональная – тетрагональная призма с пинакоидом. • Ромбическая – кирпичик. • Моноклинальная – параллелепипед с одним косым углом и 2 -мя другими прямыми. • Триклинная – косоугольный параллелепипед с неравными ребрами. • В соответствии с расположенными дополнительных узлов решетки в различных частях ячеек, все решетки подразделяются на: • Примитивную ( Р ); • Базоцентрированную ( С ); • Объемноцентрированную ( У ); • Гранецентрированную ( F );

ГЕОМЕТРИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ Элементы ограничения многогранников • Многогранником называется объемное геологическое тело, отделенное от окружающего пространства элементами ограничения. • Элементами ограничения называют геометрические образы, отделяющие многогранник от окружающего пространства. • К элементам ограничения многогранника относятся грани, ребра, вершины, двугранные и многогранные углы. • Грани – это плоские поверхности, ограничивающие многогранник от внешней среды. • Рёбра – это прямые линии, по которым пересекаются грани. • Вершины – это точки, в которых пресекаются ребра. • Двугранные углы – это углы между двумя соседними гранями. Иначе, это углы при ребрах. • Многогранные углы – это углы между несколькими гранями, сходящимися в одной вершине. Иначе, это углы при вершинах.

• • • Среди многогранных углов различают правильные и неправильные. Если при соединении концов ребер, исходящих из вершины многогранного угла, получается правильная геометрическая фигура (правильный треугольник, прямоугольник, ромб, квадрат, правильный шестиугольник и их производные), то образуется правильный многогранный угол. Если при этой же операции получается неправильная геометрическая фигура (неправильный многоугольник), то такой многогранный угол называется неправильным Различают следующие правильные многогранные углы. 1. Тригональный – при соединении концов ребер, исходящих из его вершины, образуется правильный треугольник (тригон): • 2. Ромбический 1 -го рода – соединение концов ребер, исходящих из его вершины, дает фигуру в форме ромба; • 3. Ромбический 2 -го рода – фигура, получаемая при соединении концов ребер, исходящих из его вершины, – прямоугольник: • 4. Тетрагональный – при соединении концов ребер, исходящих из его вершины, образуется квадрат (тетрагон):

• 5. Гексагональный – соединение концов ребер, исходящих из его вершины, дает правильный шестиугольник (гексагон): • Данные пять правильных многогранных углов называются основными. • Кроме того, из тригонального, тетрагонального и гексагонального углов путем их удвоения образуются следующие три производных правильных многогранных угла. • • 1. Дитригональный – образуется путем удвоения граней, составляющих тригональный угол (дитригон): • 2. Дитетрагоналный – образуется при удвоении числа граней тетрагонального угла (дитетрагон): • • 3. Дигексагональный – образуется путем удвоения числа граней, ограничивающих гексагональный угол (дигексагон):

• Во всех производных правильных многогранных углах двугранные углы равны через один, а все стороны фигуры, образованной при соединении концов ребер, исходящих из вершины, равны. • Таким образом, существует всего 8 правильных многогранных углов. Все остальные многогранные углы являются неправильными. Их возможно бесконечное количество. • Между элементами ограничения многогранников существует математическая зависимость, характеризуемая формулой Эйлера. Декарта: Г (грани) + В (вершины) = Р (ребра) + 2. • Например, в кубе 6 граней, 8 вершин и 12 рёбер. • Отсюда: 6+8=12+2. • 2. Элементы симметрии многогранников • Элементами симметрии называются вспомогательные геометрические образы (точка, линия, плоскость и их сочетания), с помощью которых мысленно можно совместить в пространстве равные грани кристалла (многогранника). • При этом под симметрией кристалла понимается закономерное повторение в пространстве равных его граней, а также вершин и ребер. • Различают три основных элемента симметрии кристаллов – центр симметрии, плоскость симметрии и оси симметрии.

• Центром симметрии называется воображаемая точка внутри кристалла, равноудаленная от его элементов ограничения (т. е. противоположных вершин, середин ребер и граней). Центр симметрии является точкой пересечения диагоналей правильной фигуры (куба, параллелепипеда). Центр симметрии обозначается буквой С, а по международной системе Германа-Могена – I. • Центр симметрии в кристалле может быть только один. Однако имеются кристаллы, в которых центр симметрии вообще отсутствует. При решении вопроса о том, имеется ли центр симметрии в Вашем кристалле, необходимо руководствоваться следующим правилом: «При наличии центра симметрии в кристалле каждой его грани соответствует равная и противоположная ей грань» . На практических занятиях с лабораторными моделями наличие или отсутствие центра симметрии в кристалле устанавливается следующим образом. Кладем кристалл какой-либо его гранью на плоскость стола. Проверяем, присутствует ли сверху равная и параллельная ей грань. Повторяем ту же операцию для каждой грани кристалла. Если каждой грани кристалла отвечает сверху равная и параллельная ей грань, то центр симметрии в кристалле присутствует. Если хотя бы для одной грани кристалла не найдется сверху равной и параллельной ей грани, то – центра симметрии в кристалле нет • •

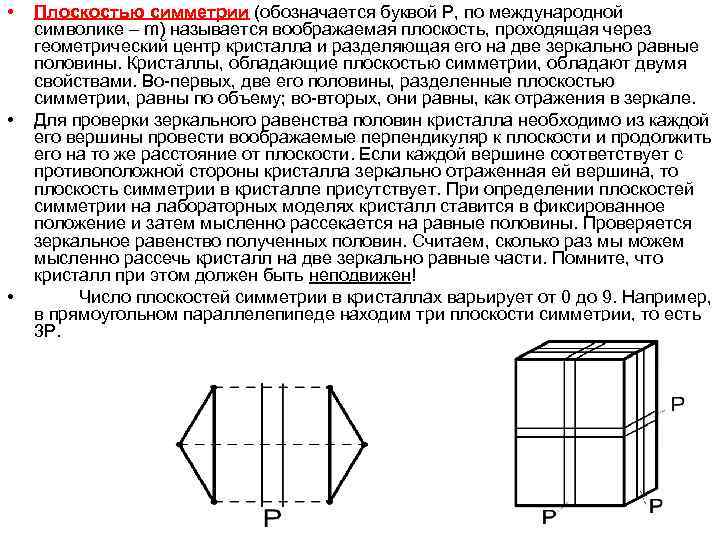• • • Плоскостью симметрии (обозначается буквой Р, по международной символике – m) называется воображаемая плоскость, проходящая через геометрический центр кристалла и разделяющая его на две зеркально равные половины. Кристаллы, обладающие плоскостью симметрии, обладают двумя свойствами. Во-первых, две его половины, разделенные плоскостью симметрии, равны по объему; во-вторых, они равны, как отражения в зеркале. Для проверки зеркального равенства половин кристалла необходимо из каждой его вершины провести воображаемые перпендикуляр к плоскости и продолжить его на то же расстояние от плоскости. Если каждой вершине соответствует с противоположной стороны кристалла зеркально отраженная ей вершина, то плоскость симметрии в кристалле присутствует. При определении плоскостей симметрии на лабораторных моделях кристалл ставится в фиксированное положение и затем мысленно рассекается на равные половины. Проверяется зеркальное равенство полученных половин. Считаем, сколько раз мы можем мысленно рассечь кристалл на две зеркально равные части. Помните, что кристалл при этом должен быть неподвижен! Число плоскостей симметрии в кристаллах варьирует от 0 до 9. Например, в прямоугольном параллелепипеде находим три плоскости симметрии, то есть 3 Р.

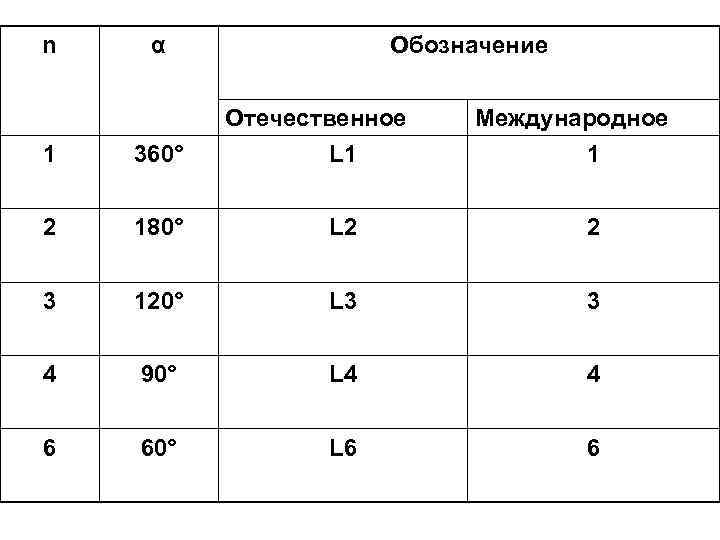
• Осью симметрии называется воображаемая линия, проходящая через • • • геометрический центр кристалла, при повороте вокруг которой кристалл несколько раз повторяет свой внешний вид в пространстве, то есть самосовмещается. Это означает, что после поворота на некоторый угол на место одних граней кристалла становятся другие, равные им грани. Основной характеристикой оси симметрии является наименьший угол поворота, при котором кристалл первый раз «повторяется» в пространстве. Этот угол называется элементарным углом поворота оси и обозначается α. Например: Элементарный угол поворота любой оси обязательно содержится целое число раз в 360°, то есть (целое число), где n – порядок оси. Таким образом, порядком оси называется целое число, показывающее, сколько раз элементарный угол поворота данной оси содержится в 360°. Иначе, порядок оси – это число «повторений» кристалла в пространстве при полном его повороте вокруг данной оси. Оси симметрии обозначаются буквой L. Порядок оси обозначается маленькой цифрой справа внизу: например, L 2. В кристаллах возможны следующие оси симметрии и соответствующие им элементарные углы поворота.

n α Обозначение Отечественное L 1 Международное 1 1 360° 2 180° L 2 2 3 120° L 3 3 4 90° L 4 4 6 60° L 6 6

• • • Осей симметрии и первого порядка в любом кристалле бесконечное количество. Поэтому на практике они не определяются. Осей симметрии 5 -го и любого порядка выше 6 -го в кристаллах вообще не существует. Эта особенность кристаллов практикуется в качестве закона симметрии кристаллов. Закон симметрии кристаллов объясняется специфичностью их внутреннего строения, а именно – наличием пространственной решетки, которая не допускает возможность осей 5 -го, 7 -го, 8 -го и так далее порядков. В кристалле может быть несколько осей одного и того же порядка. Например, в прямоугольном параллелепипеде присутствуют три оси второго порядка, то есть 3 L 2. В кубе присутствуют 3 оси четвертого порядка, 4 оси третьего порядка и 6 осей второго порядка. Оси симметрии наивысшего порядка в кристалле называют главными. Для нахождения осей симметрии на моделях во время лабораторных занятий действуют в следующем порядке. Кристалл берется кончиками пальцев одной руки за его противоположные точки (вершины, середины ребер или граней). Воображаемая ось ставится перед собой вертикально. Запоминаем какой-либо характерный внешний вид кристалла. Затем кристалл вращаем другой рукой вокруг воображаемой оси до тех пор, пока его первоначальный внешний вид не «повторится» в пространстве. Считаем, сколько раз кристалл «повторяется» в пространстве при полном повороте вокруг данной оси. Это и будет ее порядок. Аналогичным образом проверяем все другие теоретически возможные направления прохождения оси симметрии в кристалле.

• Сочетание всех элементов симметрии кристалла, записанное условными обозначениями, называется его формулой симметрии. В формуле симметрии сначала перечисляются оси симметрии, затем плоскости симметрии и последним показывается наличие центра симметрии. Между обозначениями не ставится точек или запятых. Например, формула симметрии прямоугольного параллелепипеда: 3 L 33 PC; куба – 3 L 44 L 36 L 29 PC.

• • • 3. Виды симметрии кристаллов Видами симметрии называются возможные в кристаллах сочетания элементов симметрии. Каждому виду симметрии соответствует определенная формула симметрии. Всего для кристаллов теоретически доказано наличие 32 видов симметрии. Таким образом, всего существует 32 формулы симметрии кристаллов. Все виды симметрии объединяются в 7 ступеней симметрии с учетом наличия характерных элементов симметрии. Примитивная – объединяются виды симметрии, представленные только одиночными осями симметрии разного порядка, например: L 3, L 4, L 6. Центральная – помимо одиночных осей симметрии, присутствует центр симметрии; кроме того, в присутствии четных осей симметрии появляется еще плоскость симметрии, например: L 3 С, L 4 PC, L 6 PC. Планальная (план – плоскость, греч. ) – присутствуют одиночная ось и плоскости симметрии: L 22 P, L 44 P. Аксиальная (аксис – ось, греч. ) – присутствуют только оси симметрии: 3 L 2, L 33 L 2, L 66 L 2. Планаксиальная – присутствуют оси, плоскости и центр симметрии: 3 L 23 PC, L 44 L 25 PC. Инверсионно-примитивная – наличие единственной инверсионной оси симметрии: Li 4, Li 6. Инверсионно-планальная – наличие, помимо инверсионной оси, простых осей и плоскостей симметрии: Li 44 L 22 P, Li 63 L 23 P. В каждую ступень симметрии объединяется разное количество видов симметрии: от 2 до 7.

• • • Сингонией называется группа видов симметрии, обладающих одноименной 4. Сингонии главной осью симметрии и одинаковым общим уровнем симметрии. Син – сходный, гониа – угол, дословно: сингония – сходноугольность (греч. ). Переход от одной сингонии к другой сопровождается повышением степени симметрии кристаллов. Всего выделяют 7 сингоний. В порядке последовательного повышения степени симметрии кристаллов они располагаются следующим образом. Триклинная сингония (клин – угол, наклон, по-гречески) получила название с учетом той особенности кристаллов, что между всеми гранями углы всегда косые. Кроме С, других элементов симметрии нет. Моноклинная (монос – один, по-гречески) – в одном направлении между гранями кристаллов угол всегда косой. В кристаллах могут присутствовать L 2, P и С. Ни один из элементов симметрии не повторяется хотя бы дважды. Ромбическая – получила название по характерному поперечному сечению кристаллов (вспомните углы ромбические 1 -го и 2 -го рода). Тригональная – названа по характерному поперечному сечению (треугольник) и многогранным углам (тригональный, дитригональный). Обязательно присутствует одна L 3. Тетрагональная – характерны поперечное сечение в форме квадрата и многогранные углы – тетрагональный и дитетрагональный. Обязательно присутствует L 4 или Li 4. Гексагональная – сечение в форме правильного шестиугольника, многогранные углы – гексагональный и дигексагональный. обязательно присутствие одной L 6 или Li 6. Кубическая – типична кубическая форма кристаллов. Характерно сочетание элементов симметрии 4 L 3.

• • Сингонии объединяются в 3 категории: низшую, среднюю и высшую. В низшую категорию объединяются триклинная, моноклинная и ромбическая сингонии. В среднюю категорию входят тригональная, тетрагональная и гексагональная сингонии. Характерна одна главная ось симметрии. К высшей категории относится одна кубическая сингония. В отличие от предыдущих категорий, для нее характерно несколько главных осей симметрии.

5. Понятие о простой форме, комбинации и габитусе • На практических занятиях с лабораторными моделями в качестве простой формы рассматривается совокупность равных граней кристалла. Если все грани кристалла одинаковы, то он в целом является простой формой. Наоборот, если все грани кристалла не равны по форме и геометрическим очертаниям, то каждая из его граней является отдельной простой формой. Таким образом, в кристалле будет столько простых форм, сколько у него геометрических типов граней, учитывая также их размеры. Например, в прямоугольном параллелепипеде 3 типа граней. Типы граней в прямоугольном параллелепипеде Следовательно, он состоит из 3 простых форм. Каждая из них в свою очередь, состоит из 2 равных параллельных граней. Названия простым формам даются в зависимости от числа граней и их взаимного расположения. Существует всего 47 простых форм, каждая из которых

• Для определения простых форм на практических занятиях необходимо равные между собой грани мысленно продолжить до их взаимного пересечения. Полученная при этом воображаемая фигура и будет искомой простой формой. • Среди простых форм различают два вида: открытые и закрытые. Грани открытой простой формы не замыкают пространство со всех сторон. Наоборот, грани закрытой простой формы при их взаимном продолжении в пространстве со всех сторон закроют какую-то его часть. • Сочетания простых форм, образующих кристаллы, называются сложными формами, или комбинациями. В комбинации будет столько простых форм, сколько в ней типов граней. Одна открытая простая форма никогда не сможет образовать кристалл, она может встречаться только в комбинации с другими простыми формами. Комбинаций в природе бесконечное количество. • Под габитусом кристалла понимается преобладающая по площади граней простая форма. Название габитуса совпадает с названием простой формы, но дается как определение (например, простая форма – куб, габитус – кубический). Если ни одна из простых по площади граней не преобладает (или трудно это оценить), габитус называется смешанным, или комбинированным.

• 6. Порядок разбора моделей кристаллов • При изучении моделей кристаллов на практических занятиях дается характеристика следующих данных: • 1) формула симметрии кристалла; • 2) сингония; • 3) вид симметрии; • 4) простые формы; • 5) габитус.