Основы криптологии 1 Криптология область науки техники

Основы криптологии (1) Криптология – область науки, техники и практической деятельности, связанная с разработкой, применением и анализом криптографических систем защиты информации Криптология: • криптография • криптоанализ • инженерно-криптографический анализ 1

Основы криптологии (2) Задачи криптографии: • обеспечение конфиденциальности • обеспечение имитостойкости • обеспечение неотказуемости Источник угроз – криптоаналитик Нарушение безопасности, обеспечиваемой криптопреобразованиями - компрометация (взлом, раскрытие) криптосистемы 2

Основы криптологии (3) Основные характеристики криптосистемы: • криптостойкость • производительность 3

История криптологии (1) • … - 1949 г. – Эра донаучной криптографии • 1949 г. – К. Шеннон «Теория связи в секретных системах» • 1975 г. – первый открытый стандарт шифрования США DES • 1975 г. – Криптография с открытым ключом • 1989 г. – открытый стандарт шифрования РФ ГОСТ 28147 -89 4

История криптологии (2) • 2002 г – улучшенный стандарт шифрования AES • 2000 г – криптография на эллиптических кривых • > 2015 – квантовая криптография квантовые компьютеры 5

Системы шифрования (1) • Основные понятия • Шифр - семейство обратимых преобразований открытых сообщений М в зашифрованные сообщения С и обратно, каждое из которых определяется некоторым параметром, называемым ключом 6

Системы шифрования (2) • Е – параметрическое множество преобразований (функций) зашифрования • D – параметрическое множество преобразований (функций) расшифрования • Ключевая система К = (ke, kd) • C = Eke(M) • M = Dkd(C) = Dkd(Eke(M)) 7

Системы шифрования (3) Криптостойкость Принцип Керкхоффа Задачи дешифрования: § Зная С, восстановить М или kd § Зная М и С, восстановить kd § Специальным образом выбирая М и зная С, восстановить kd 8

Классификация шифрсистем 1. Симметричные (ke = kd) 1. 1 Блочные 1. 1. 1 Простые 1. 1. 2 Составные 1. 1. 2. 1 Итеративные 1. 2 Потоковые 1. 2. 1 Синхронные 1. 2. 2 Самосинхронизирующиеся 2. Асимметричные (ke ≠ kd)

Простые шифры 1. Шифр перестановки 2. Шифр подстановки 2. 1 Простая подстановка Шифр Цезаря 2. 2 Полиграммная одноалфавитная подстановка 2. 3. Монограммная сложная (полиалфавитная) подстановка 2. 4. Полиграммная сложная (полиалфавитная) подстановка 10

Простые шифры • Система шифрования Цезаря • Зашифрование • Расшифрование

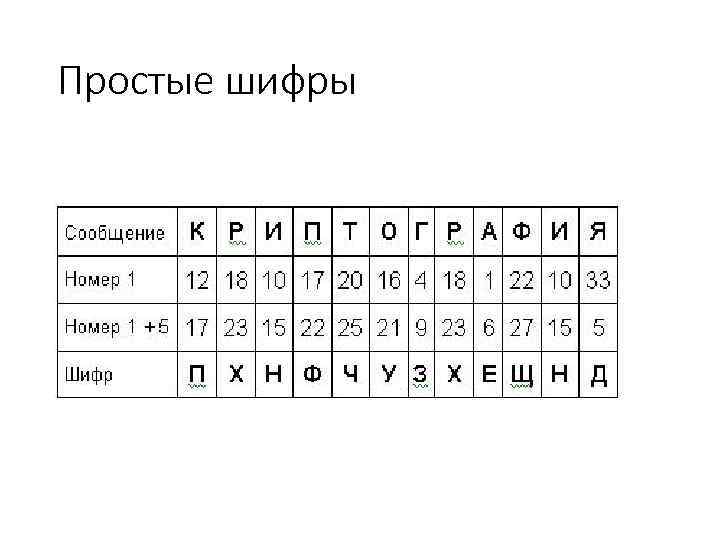
Простые шифры

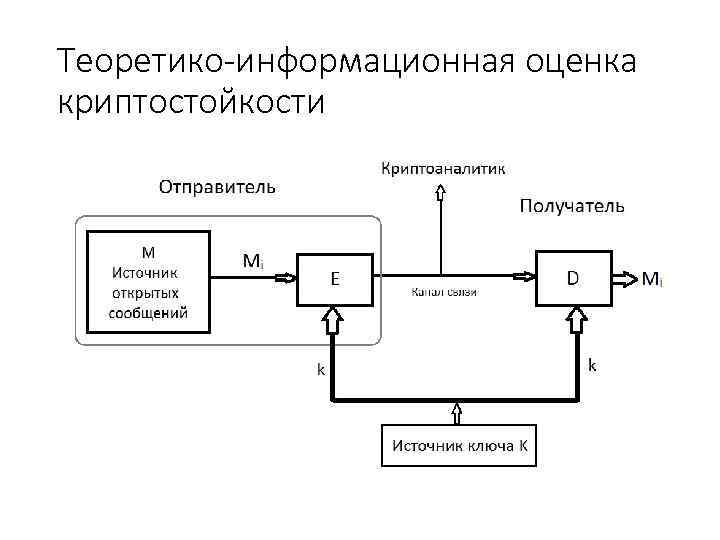
Теоретико-информационная оценка криптостойкости

Теоретико-информационная оценка криптостойкости (1) Модель Шеннона 1. Симметричная шифрсистема 2. Вероятностная природа источников М и К. 3. Абсолютно безопасный канал доставки ключа kd 4. Смена ключа после передачи каждого сообщения 5. Криптоанализ на основе только перехваченного шифртекста 6. Криптоаналитик обладает неограниченными ресурсами 14

Теоретико-информационная оценка криптостойкости (2) Совершенная секретность (безопасность) I = H (M) - HCj (M) = 0 Необходимое и достаточное условие Pr (Mi ) = Pr. Cj (Mi) для всеx Mi и Сj Граница Шеннона || K || ≥ ||M|| 15

Теоретико-информационная оценка криптостойкости (3) Ненадежность шифра: НCj (К) = - ∑ Pr. Cj (Mi)) lg (Pr. Cj (Mi)) Расстояние единственности НCj (Ne) ≈ 0 Оценка расстояния единственности Ne = L K / D 16

Теоретико-сложностная оценка криптостойкости (1) Учет ограниченности ресурсов к/а Объекты оценки: • математичесая модель шифра • конкретная реализация шифра Критерии практической стойкости • вычислительно-сложностный • временной • стоимостный 17

Теоретико-сложностная оценка криптостойкости (2) Wр – рабочая характеристика шифра Wрд – достигнутая рабочая характеристика шифра Wрд ≥ Wр Методы криптоанализа: • универсальные (метод «грубой силы» ) • аналитические 18

Теоретико-сложностная оценка криптостойкости (3) Предположительно стойкий шифр: Wрд ≥ Wгс ≥ Wо Wгс = 2 Lk § Базовая стойкость Wо ≥ 2 128 § Средняя стойкость Wо ≥ 2 192 § Высокая стойкость Wо ≥ 2 256 W рд = F (квалификация криптоаналитика)

Теоретико-сложностная оценка криптостойкости (4) Временная сложность: Твскд = Wрд / Р Тгс = Wгс / Р Р – вычислительный ресурс к/а Предположительно стойкий шифр Твскд ≥ Тгс ≥ То

Теоретико-сложностная оценка криптостойкости (5) № п/п Длина ключа Вычислительная мощность криптоаналитика 10**6 тест/сек 10**12 тест/сек 1 56 1140 лет 10 час 2 64 500 тыс. лет 107 дней 3 128 5*10 **24 лет 5*10**18 21

Теоретико-сложностная оценка криптостойкости (6) Сетевой криптоанализ Динамический характер оценки криптостойкости

Криптоанализ с использованием побочных каналов (Side-channel and fault attacks) § электромагнитное излучение § измерение времени выполнения § потребляемая мощность § sofeware based attack: - cache attacks - branch prediction analysis § fault attacks 23

Криптоанализ с использованием побочных каналов (Side-channel and fault attacks) • Анализ побочных каналов→Дополнительная информация→ • Уменьшение сложности криптоанализа

Принципы построения современных блочных шифров (1) Базовые параметры блочного шифра: Lb – длина блока открытого текста М Lk – длина криптографического ключа Выбор – из условия стойкости к универсальным методам криптоанализа

Принципы построения современных блочных шифров (2) Современные рекомендации: • низкий (базовый) уровень Lb = 64 бит Lk = 128 бит • средний уровень Lb = 128 бит Lk = 192 бит • высокий уровень Lb = 128 бит Lk = 256 бит

Итеративные блочные шифры Требования к шифрпреобразованию: 1. Диффузия (рассеивание) – свойство шифра, при котором каждый бит открытого текста и ключа влияет на все биты криптограммы. 2. Конфузия (перемешивание) – свойство шифра скрывать (затруднять использование) статистическую зависимость между символами открытого текста, ключа и шифрограммы. 3. Стойкость к современным методам криптоанализа при использовании атаки с выбранным открытым текстом

Итеративные блочные шифры Основные параметр: • Архитектура (S-P сеть, сеть Фейстеля) • Количество циклов (раундов, итераций NR) • Вид функции преобразования раунда f • Схема генерации расширенного ключа K = (k 1, k 2, …k. NR)

Итеративные блочные шифры Cовременные методы криптоанализа: - Дифференциальный криптоанализ Анализирует эволюцию разности (расстояния Хэмминга) в процессе шифрования - Линейный криптоанализ Использует линейные приближения для описания работы блочного шифра, которые позволяют предсказать битов ключа, если известно много открытых текстов и соответствующих им шифртекстов.

Шифры первого поколения Заданная криптостойкость при min используемых ресурсов США - DES РФ - ГОСТ 28147 -89

Шифры первого поколения Характерные особенности: 1. Однородная структура алгоритма шифрования. 2. Фиксированный минимальный размер блока (Lb =64 бит) 3. Фиксированный размер ключа 4. Принадлежность к сбалансированным сетям Фейстеля 5. Простая структура преобразования раунд

Сеть Фейстела Зашифрование M=L 0||R 0 Li = Ri-1 Ri = Li-1 XOR f( Ri-1, ki ) i = 1, 2, … , (NR -1) Для последнего цикла L NR = L (NR-1) XOR f(R (NR -1) , k. NR ) R NR = R (NR -1) С = L NR || R NR

Сеть Фейстела Расшифрование С = L NR || R NR = LD 0 || RD 0 LDi = RDi-1 RDi = LDi-1 XOR f( RDi-1, k (NR+1)-i) i = 1, 2, … , (NR -1) Для последнего цикла NR LDNR = LD (NR-1) XOR f( RD (NR -1), k 1 ) RD NR = RD (NR -1) М = LD NR || RD NR

Сеть Фейстела • Свойства • 1. В каждом раунде преобразуется только половина блока • 2. Обратное преобразование может быть реализовано по той же, что и прямое, но при инверсном порядке использования расширенного ключа • 3. Для выполнения п. 2 преобразование последнего раунда отличается по внешнему виду от остальных • 4. Гарантируется обратимость преобразования независимо от вида функции шифрования (может быть даже необратимой

Сеть Фейстела • 4. Размер ключа раунда равна половине длины блока • 5. Четное число раундов

Блочный шифр ГОСТ 28147 -89 Основные характеристики: Итеративный блочный шифр Размер блока фиксированный Lb = 64 бит Размер ключа фиксированный Lk = 256 бит Архитектура - сеть Фейстеля Количество раундов NR = 32

Блочный шифр ГОСТ 28147 -89 Зашифрование M = R 0 || L 0 Li = Ri-1 XOR f (Li-1[+]ki) Ri = Li-1 i = 1, 2, … , 31 где f - функция шифрования ki - i-й элемент расширенного ключа i = 1, 2, …, 31 – номер раунда [+] – сложение по модулю 232

Блочный шифр ГОСТ 28147 -89 Для последнего раунда L 32 = L 31 R 32 = R 31 XOR f (L 31[+]k 32) С = L 32||R 32

Блочный шифр ГОСТ 28147 -89 Расшифрование С = L 32||R 32 = LD 0 || RD 0 LDi = RDi-1 XOR f (Li-1[+]k(33 –i)) Ri = Li-1 i = 1, 2, … , 31 Для последнего раунда L 32 = L 31 R 32 = R 31 XOR f (L 31[+]k 32) M = R 0 || L 0 С = L 32||R 32

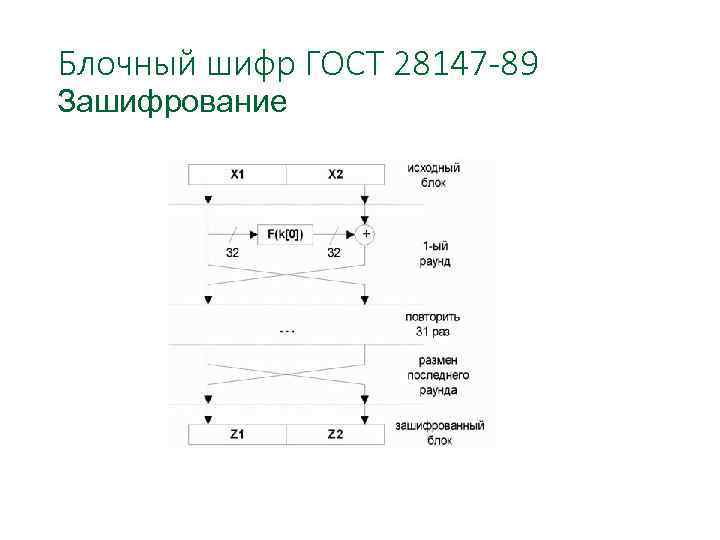
Блочный шифр ГОСТ 28147 -89 Зашифрование

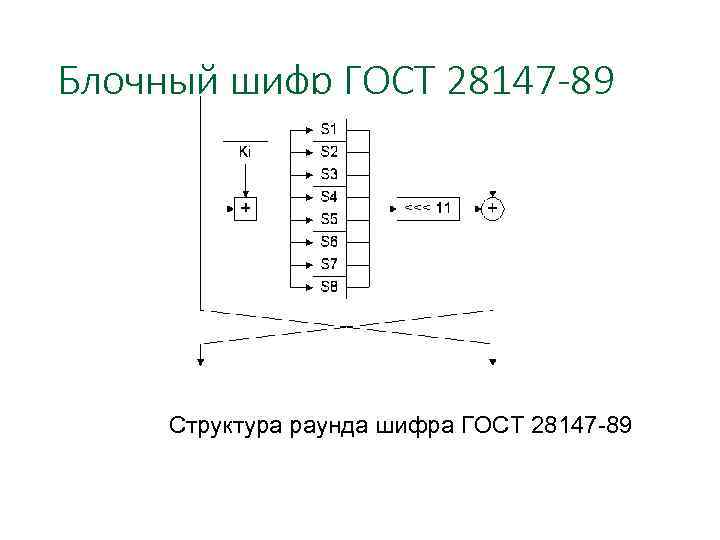
Блочный шифр ГОСТ 28147 -89 Структура раунда шифра ГОСТ 28147 -89

Блочный шифр ГОСТ 28147 -89 Формирование расширенного ключа • Зашифрование • К = К 0||К 1||К 2||К 3||К 4||К 5||К 6||К 7 || • ki = Kj • i = 1, 2, …, 24 • j = (i-1) mod 8 • i = 25, 26, . . . , 32 • j = 32 -i

Блочный шифр ГОСТ 28147 -89 Формирование расширенного ключа • Зашифрование • К 0 К 1 К 2 К 3 К 4 К 5 К 6 К 7 • К 7 К 6 К 5 К 4 К 3 К 2 К 1 К 0

Блочный шифр ГОСТ 28147 -89 Формирование расширенного ключа • Расшифрование • К 0 К 1 К 2 К 3 К 4 К 5 К 6 К 7 • К 7 К 6 К 5 К 4 К 3 К 2 К 1 К 0

Шифры второго поколения (2000 г. ) Требования 1. Удовлетворять современным требованиям к криптостойкости 2. Возможность эффективной программной, микропрограммной и аппаратной реализации 3. Возможность варьировать базовые параметры шифрпреобразования Победитель конкурса – алгоритм Rijndael

Блочный шифр АЕS Основные характеристики: • Итеративный блочный шифр • Размер блока Lb = 128*/192/256 бит • (Nb = 4/6/8 слов) • Размер ключа Lk = 128/192/256 бит • (Nk = 4/6/8 слов) • Архитектура - сеть Square ( «Квадрат» ) • Количество раундов NR = 10/12/14

Протоколы шифрования блочных шифров с секретным ключом (режимы, modes of operations) Простая замена Гаммирование с обратной связью IEEE P 1619 Стандарт криптографической защиты данных на блок-ориентированных устройствах хранения

Режим простой замены (ECB) • М = < М 1, М 2, …, Мn > • Зашифрование • Ci = Ek(Mi) • Расшифрование • Mi = Dk(Ci) ||Мi|| = 64

Режим простой замены (ECB) • Особенности 1. Каждый блок шифруется независимо 2. M'i = Mi xor ei → C‘i = Ci xor ei → М‘i размножение ошибок в пределах блока (псевдостохастическая последовательность 3. Длина М кратна длине блока 4. Если Mi=Mj ↔ Ci = Cj

Режим простой замены

Режим простой замены (ECB) • Область применения Другие протоколы и механизмы криптозащиты, в т. ч. шифрование ключей, генерация ключей

Режим гаммирования (OFB, Counter) • М = < М 1, М 2, …, Мn > • Зашифрование • Гi = Еk (wi) • Ci = Mi xor Гi • C = <S, C 1, C 2, … Cn> • S - синхропосылка

Режим гаммирования (OFB, Counter) • Расшифрование • C = <S, C 1, C 2, … Cn> • Гi = Еk (wi) • Mi = Ci xor Гi • М = < М 1, М 2, …, Мn > • S - синхропосылка

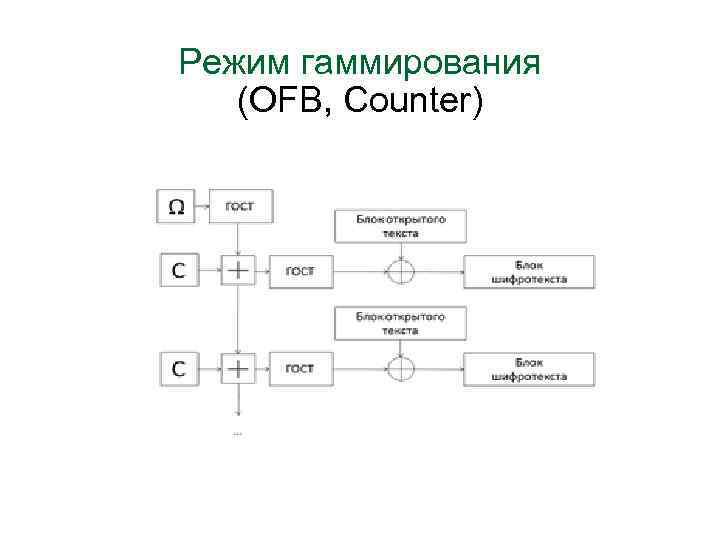
Режим гаммирования (OFB, Counter)

Режим гаммирования Формирование реккурентной последовательности wi = f (wi-1) w 0 = Еk (S) Wi = Yi ║Zi Yi =(Yi-1 + C 2) mod 232 Zi = (Zi-1 + C 1) mod (232 -1) Wi ≠ Wi-1 Период = 232 * (232 -1)

Режим гаммирования Особенности 1. Гi = f (K, S, i) Если Mi=Mj, Гi ≠ Гj → Ci ≠ Cj 2. Уникальность S 3. Длина М (С) может быть не кратны длине блока 4. M'i = Mi xor ei ↔ C‘i = Ci xor ei 5. Г'i ≠ Гi → M'i = (Ci xor Г'i ) ≠ (Mi = Ci xor Гi ) Синхронный блочный шифр

Режимы гаммирования, гамммирования с ОС

Режим гаммирования Область применения 1. Шифрование информации с избыточностью 2. Неполное шифрование 3. Шифрование информации с произвольным доступом

Режим гаммирования c ОС (CFB) • Зашифрование • М = < М 1, М 2, …, Мn > • Ci = Mi xor Гi • Гi = Ek (Ci-1) • Г 1 = Ek (S) • C = <S, C 1, C 2, … Cn>

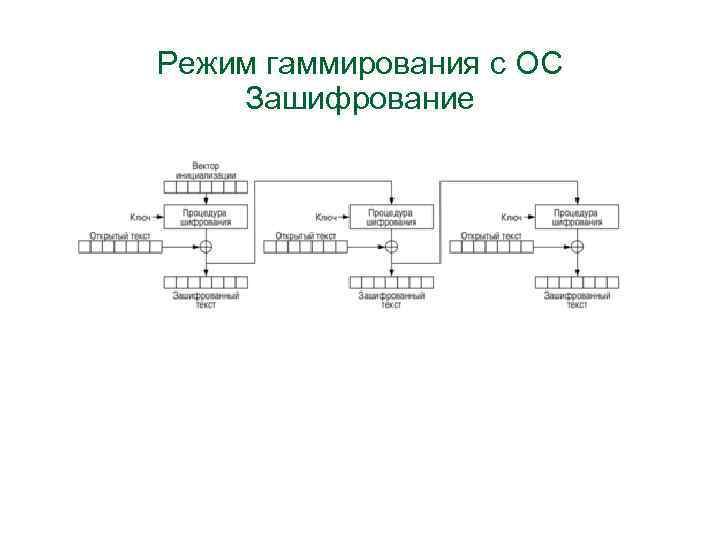
Режим гаммирования c ОС Зашифрование

Режим гаммирования c ОС • Расшифрование • C = <S, C 1, C 2, … Cn> • M’i = C'i xor Г'i • Г'i = Еk (C'i-1) • М’ = < М’ 1, М’ 2, …, М’n >

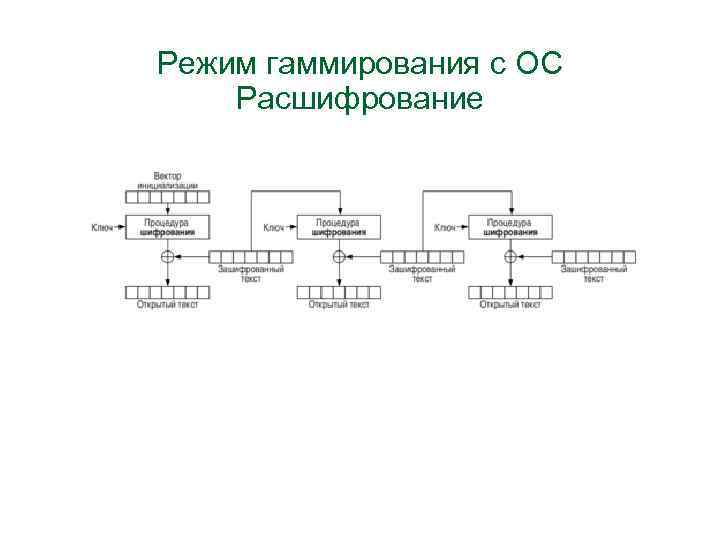
Режим гаммирования c ОС Расшифрование

Режим гаммирования c ОС 1. Зашифрование Гi = f (K, S, M 1, M 2, …M(i-1)) Если Mi=Mj, то Гi ≠ Гj → Ci ≠ Cj Расшифрование Гi = f (K, S, С’(i-1), C’i) 2. Длина М (С) может быть не кратны длине блока

Режим гаммирования c ОС 3. Размножение ошибок 3. 1. M'i = Mi xor ei → C‘i = Ci xor ei C‘j ≠ Ci j = i+1, i+2, … 3. 2 C'i = Ci xor ei M‘i = Mi xor ei M‘j+1 ≠ Mi+1 M‘j = Mj j = (i+2), (i+3

Режим гаммирования c ОС 4. С’ = <S, C 1, C 2, …, C (i-1) , C(i+1), …, Cn> М’ = < М 1, М 2, …, М (i-1) , М’(i+1), …, Мn > Самосинхронизирующийся блочный шифр

Режим гаммирования c ОС • Область применения Системы с возможной потерей блочной синхронизации