ОКТ_ЭЛЕКТРИЧЕСКОЕ ПОЛЕ.ppt
- Количество слайдов: 148

ОСНОВЫ КАБЕЛЬНОЙ ТЕХНИКИ
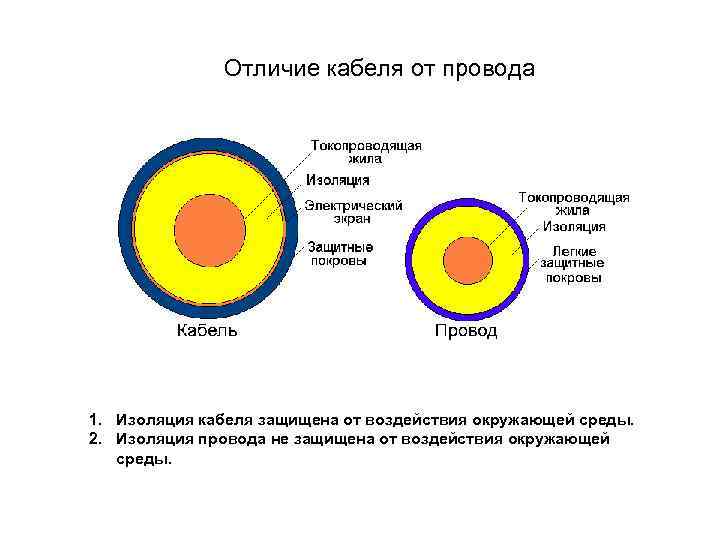
Отличие кабеля от провода 1. Изоляция кабеля защищена от воздействия окружающей среды. 2. Изоляция провода не защищена от воздействия окружающей среды.

МОНТАЖНЫЕ ПРОВОДА И ПРОВОДА ПИТАНИЯ Диапазон сечений монтажных проводов – от 0, 03 до 2, 5 мм 2, а проводов питания – от 0, 35 до 1000 мм 2. Монтажные провода – это провода слабого тока, поэтому сечение жил выбирается исходя из падения напряжения, а не по допустимому току. Монтажные провода используются малыми длинами, по этой причине падение напряжения незначительно даже для малых сечений. Сечение жил проводов питания выбирается исходя из передаваемого по ним тока.

КЛАССИФИКАЦИЯ КАБЕЛЬНЫХ ИЗДЕЛИЙ Классификация по назначению 1. Силовые кабели – для передачи электроэнергии на промышленной частоте 50 Гц (Европа) и 60 Гц (Америка). 2. Кабели связи информации. (электрические или оптические) – для передачи 3. Радиочастотные кабели – для передачи информации и энергии на высокой частоте. 4. Контрольные кабели и кабели управления маломощных сигналов. – для передачи

Классификация по виду изоляции 1. Полиэтиленовая; 2. Поливинилхлоридная и т. д. 3. Резиноваяи т. д.
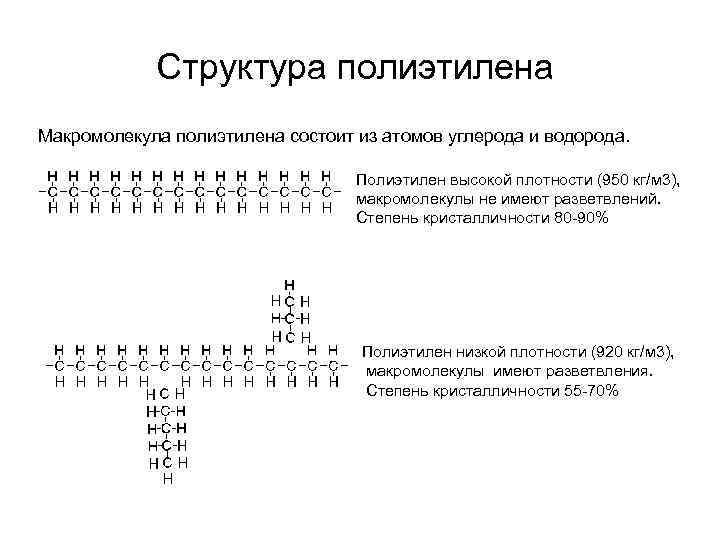
Структура полиэтилена Макромолекула полиэтилена состоит из атомов углерода и водорода. Полиэтилен высокой плотности (950 кг/м 3), макромолекулы не имеют разветвлений. Степень кристалличности 80 -90% Полиэтилен низкой плотности (920 кг/м 3), макромолекулы имеют разветвления. Степень кристалличности 55 -70%
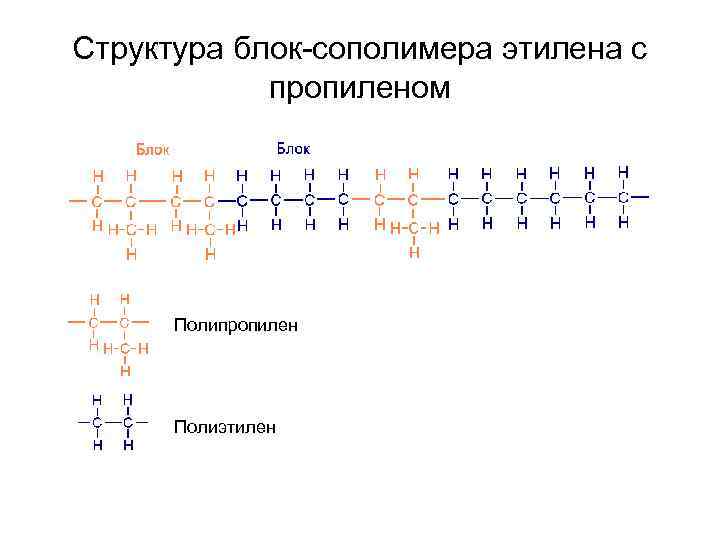
Структура блок-сополимера этилена с пропиленом Полипропилен Полиэтилен
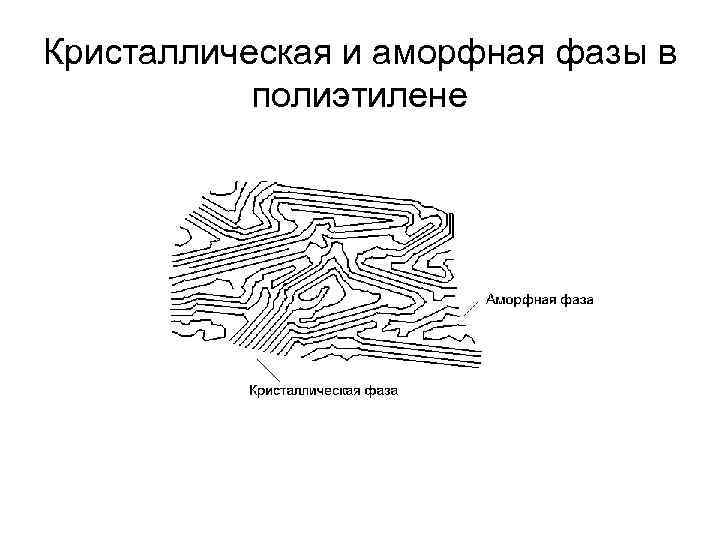
Кристаллическая и аморфная фазы в полиэтилене
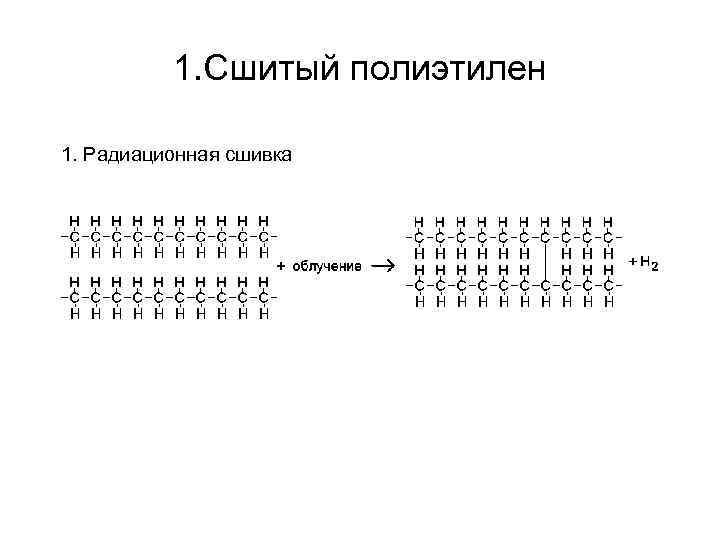
1. Сшитый полиэтилен 1. Радиационная сшивка
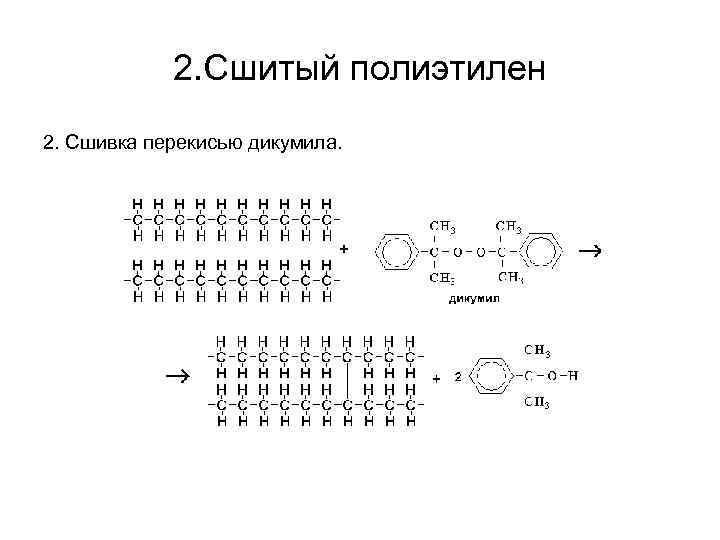
2. Сшитый полиэтилен 2. Сшивка перекисью дикумила.
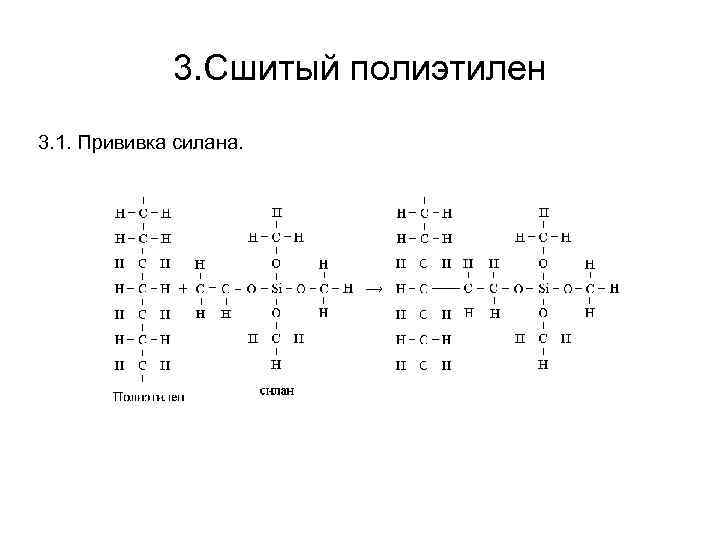
3. Сшитый полиэтилен 3. 1. Прививка силана.

3. 2. Сшивка полиэтилена с привитым силаном.

СИЛОВЫЕ КАБЕЛИ СО СШИТОЙ ПОЛИЭТИЛЕНОВОЙ ИЗОЛЯЦИЕЙ Марка кабеля АПв. П
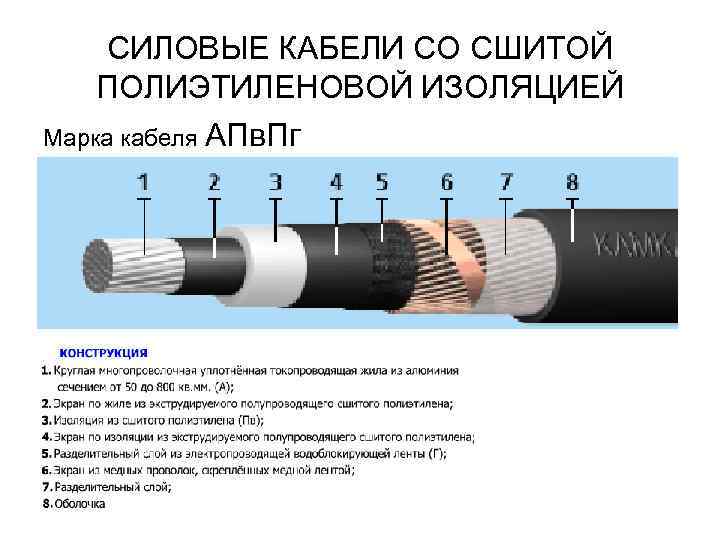
СИЛОВЫЕ КАБЕЛИ СО СШИТОЙ ПОЛИЭТИЛЕНОВОЙ ИЗОЛЯЦИЕЙ Марка кабеля АПв. Пг

СИЛОВЫЕ КАБЕЛИ СО СШИТОЙ ПОЛИЭТИЛЕНОВОЙ ИЗОЛЯЦИЕЙ Марка кабеля АПв. П 2 г

Классификация по области применения 1. Авиационные, автомобильные и тракторные. 2. Аэродромные. 3. Геофизические; 4. Контрольные, сигнализации и блокировки на железных дорогах. 5. Судовые. 6. Шахтные. 7. Управления для подвижных механизмов. 8. Горных разработок и землеройных работ; 9. Нефтяных промыслов; 10. Электросварки. 11. Подвижного состава (электрический транспорт).

АВИАЦИОННЫЕ Предназначены для фиксированного монтажа бортовой электрической сети авиационной техники 1. Токопроводящая жила из медных посеребренных проволок. 2. Изоляция из полиимидно-фторопластовых пленок. 3. Экран из медных посеребренных проволок. АВТОТРАКТОРНЫЕ 1. Токопроводящая жила из медных проволок. 2. Изоляция из ПВХ пластиката
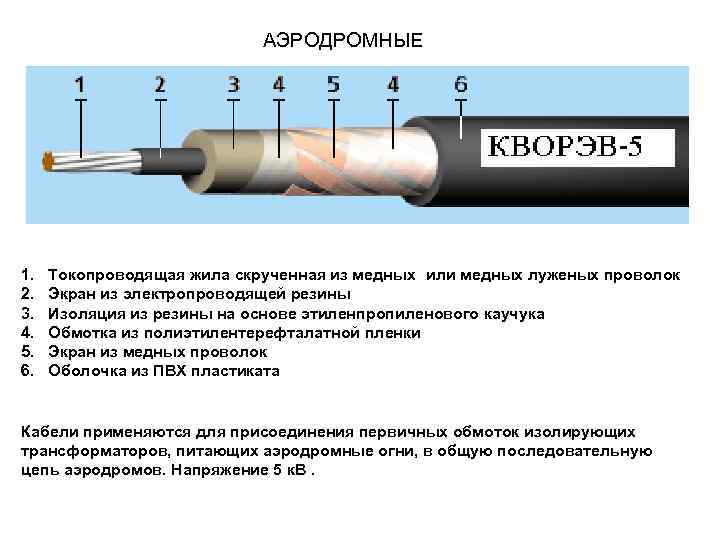
АЭРОДРОМНЫЕ 1. 2. 3. 4. 5. 6. Токопроводящая жила скрученная из медных или медных луженых проволок Экран из электропроводящей резины Изоляция из резины на основе этиленпропиленового каучука Обмотка из полиэтилентерефталатной пленки Экран из медных проволок Оболочка из ПВХ пластиката Кабели применяются для присоединения первичных обмоток изолирующих трансформаторов, питающих аэродромные огни, в общую последовательную цепь аэродромов. Напряжение 5 к. В.

СИГНАЛЬНО-БЛОКИРОВОЧНЫЕ Предназначены для сигнализации блокировки на железных дорогах
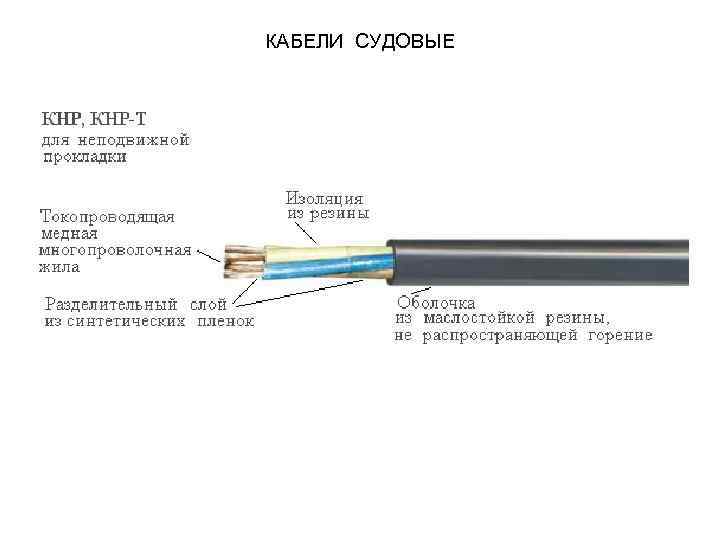
КАБЕЛИ СУДОВЫЕ
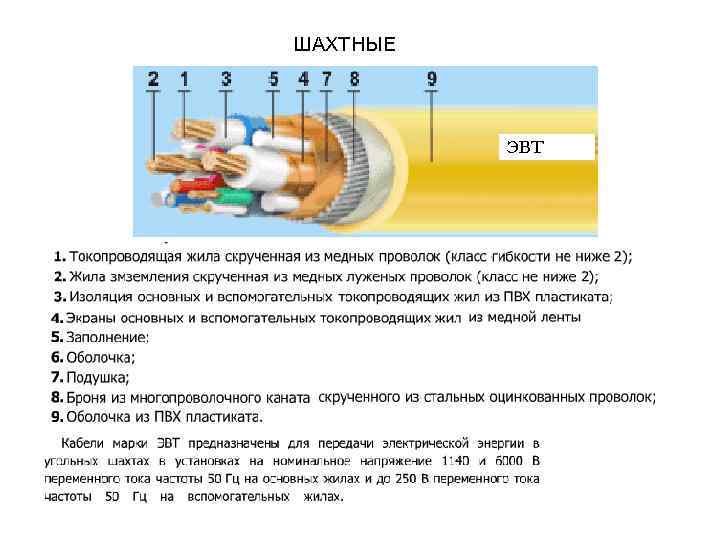
ШАХТНЫЕ

ДЛЯ ГОРНЫХ ЗАЗРАБОТОК И ЗЕМЛЕРОЙНЫХ РАБОТ
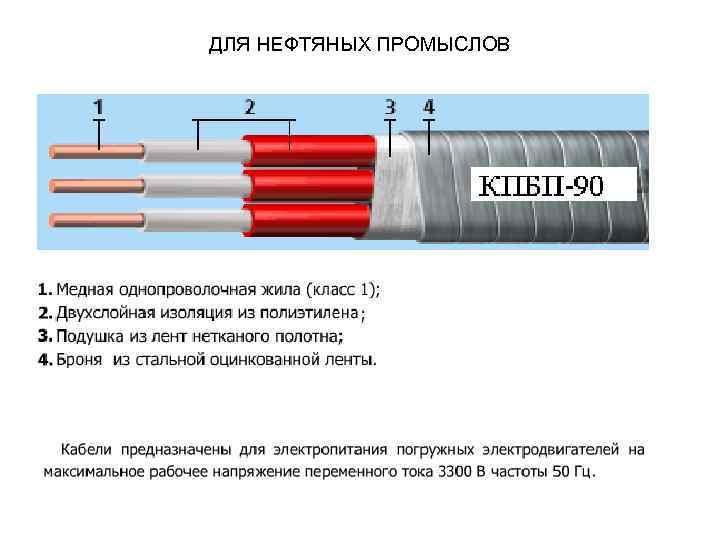
ДЛЯ НЕФТЯНЫХ ПРОМЫСЛОВ
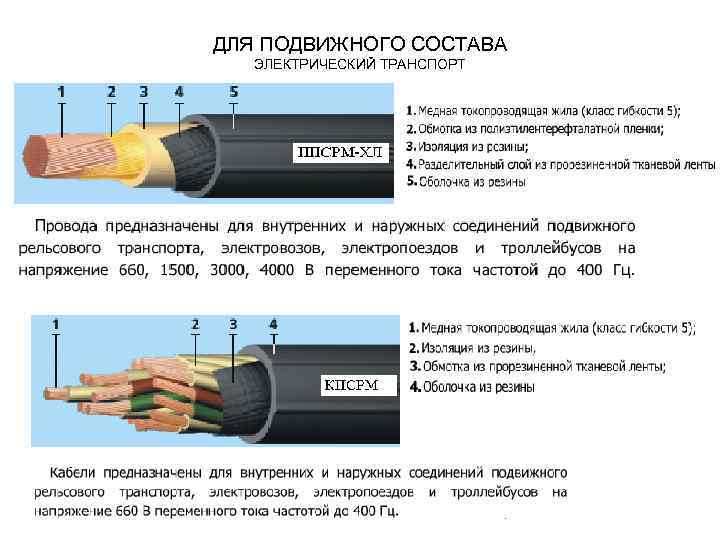
ДЛЯ ПОДВИЖНОГО СОСТАВА ЭЛЕКТРИЧЕСКИЙ ТРАНСПОРТ
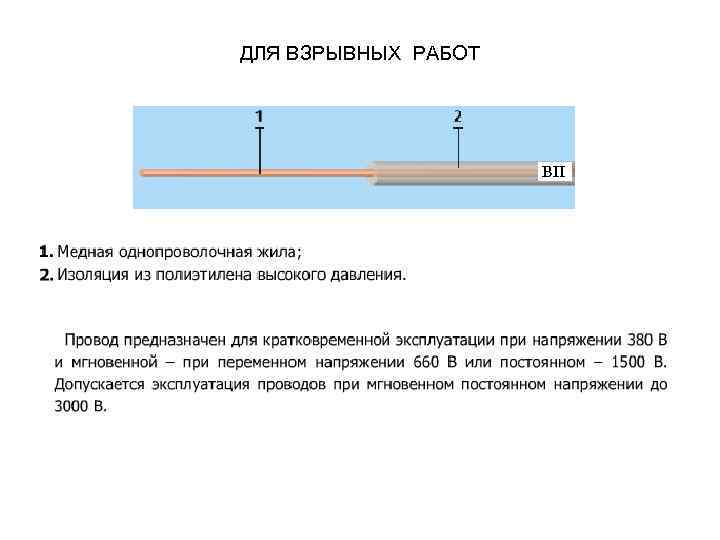
ДЛЯ ВЗРЫВНЫХ РАБОТ
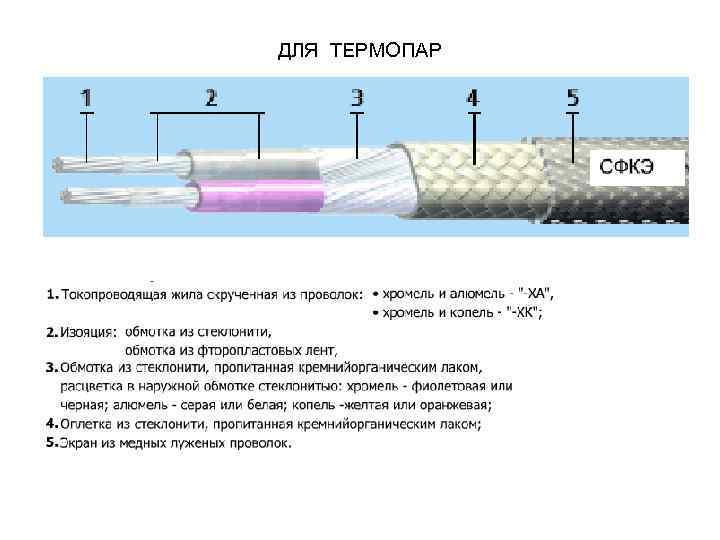
ДЛЯ ТЕРМОПАР
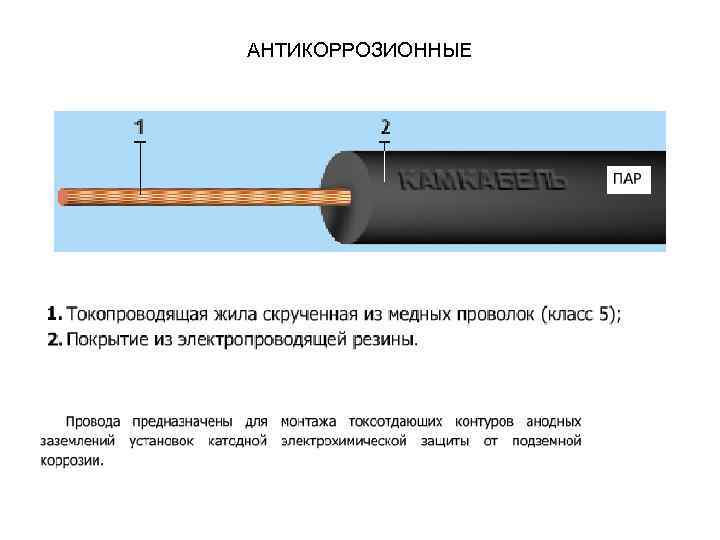
АНТИКОРРОЗИОННЫЕ

Классификация по группам однородной продукции (по технологии производства) 1) провода неизолированные для воздушных линий электропередачи; 2) провода самонесущие изолированные; 3) провода неизолированные контактные; 4) провода неизолированные гибкие; 5) кабели силовые для стационарной прокладки на напряжение менее 1 к. В; 6) кабели силовые для стационарной прокладки на напряжение 1 к. В и выше; 7) кабели силовые для нестационарной прокладки на напряжение 1 к. В; 8) провода силовые для электрических установок; 9) провода силовые бытового назначения; 10) провода автотракторные; 11) провода и шнуры осветительные; 12) провода для выводов обмоток электрических машин; 13) провода силовые общего назначения; 14) провода для взрывных работ; 15) провода и кабели нагревательные; 16) провода и кабели подвижного состава; 17) кабели управления; 18) кабели контрольные; 19) кабели сигнально-блокировочные; 20) кабели и провода термоэлектродные; 21) кабели с минеральной изоляцией; 22) кабели дальней связи; 23) кабели связи телефонные; 24) кабели зоновой связи; 25) кабели связи стационарные и распределительные; 26) провода связи телефонные распределительные и радиотрансляционные; 27) провода и кабели связи полевые; 28) шнуры слаботочные; 29) кабели для компьютерных сетей; 30) провода и кабели монтажные; 31) провода и кабели бытовые; 32) кабели и провода для геофизических работ; 33) кабели судовые; 34) кабели волоконно-оптические; 35) кабели радиочастотные; 36) провода обмоточные с эмалевой изоляцией; 37) провода обмоточные с волокнистой и другими видами изоляции; 38) прокат цветной.
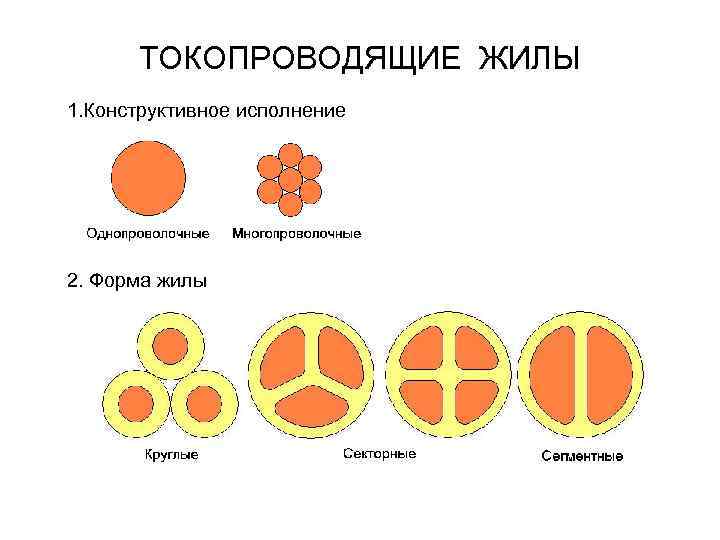
ТОКОПРОВОДЯЩИЕ ЖИЛЫ 1. Конструктивное исполнение 2. Форма жилы
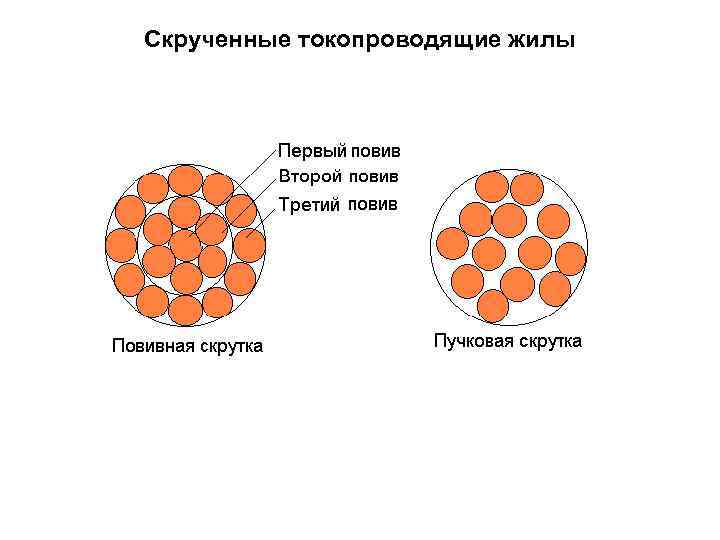
Скрученные токопроводящие жилы

ОДНОНАПРАВЛЕННАЯ И РАЗНОНАПРАВЛЕННАЯ СКРУТКИ

СВОЙСТВА СКРУЧЕННЫХ ЖИЛ При повивной скрутке направление скрутки повивов может чередоваться или оставаться одним и тем же. Наиболее часто применяют чередование направлений скрутки. Свойства жил с чередующимся направлением скрутки повивов: 1) при растяжении жилы не теряют круглой формы и растягиваются незначительно; 2) такие жилы менее гибкие, чем жилы одного направления скрутки. Свойства жил с одним направлением скрутки повивов: 1) при растяжении они сильно удлиняются и теряют круглую форму; 2) эти жилы более гибкие, чем жилы с чередующимся направлением скрутки повивов. Свойства жил пучковой скрутки: 1) каждая проволока в жиле расположена произвольно; 2) все проволоки имеют одно направление скрутки; 3) эти жилы более гибкие, чем жилы повивной скрутки; 4) жилы менее устойчивы, чем жилы правильной скрутки.
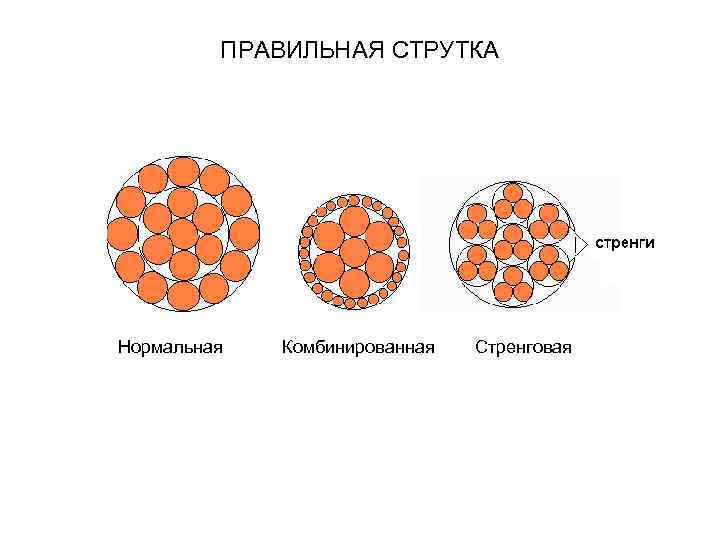
ПРАВИЛЬНАЯ СТРУТКА Нормальная Комбинированная Стренговая

НОМИНАЛЬНЫЙ РЯД СЕЧЕНИЙ ТОКОПРОВОДЯЩИХ ЖИЛ В России принят следующий ряд номинальных сечений токопроводящих жил силовых кабелей: 0, 03; 0, 05; 0, 08; 0, 12; 0, 35; 0, 75; 1, 0; 1, 2; 1, 5; 2, 0; 2, 5; 3, 0; 4, 0; 5, 0; 6, 0; 8, 0; 16; 25; 35; 50; 70; 95; 120; 150; 185; 240; 300; 400; 500; 625; 800; 1000 мм 2. Этот ряд сечений построен в соответствии с рекомендациями Международной электротехнической комиссии (МЭК): одно сечение отличается от другого в. Эти рекомендации МЭК не распространяются на обмоточные провода, неизолированные провода для ЛЭП, кабели и провода связи, так как геометрические размеры жил для них вычисляются исходя из электрических параметров кабелей.
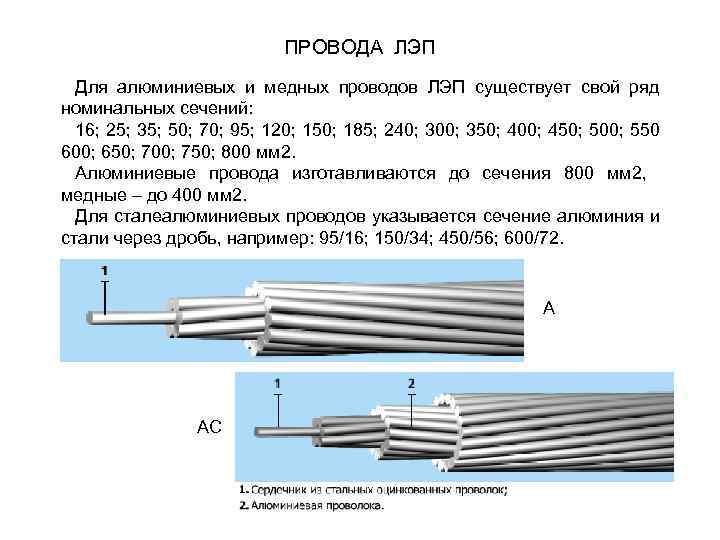
ПРОВОДА ЛЭП Для алюминиевых и медных проводов ЛЭП существует свой ряд номинальных сечений: 16; 25; 35; 50; 70; 95; 120; 150; 185; 240; 300; 350; 400; 450; 500; 550 600; 650; 700; 750; 800 мм 2. Алюминиевые провода изготавливаются до сечения 800 мм 2, медные – до 400 мм 2. Для сталеалюминиевых проводов указывается сечение алюминия и стали через дробь, например: 95/16; 150/34; 450/56; 600/72. А АС
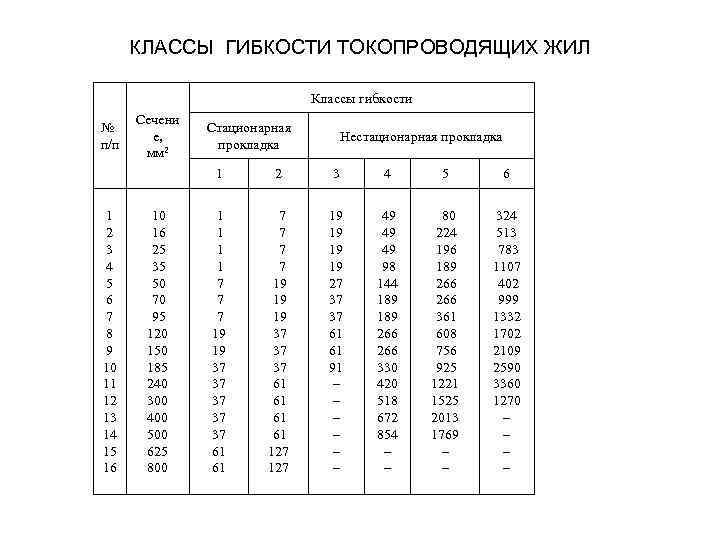
КЛАССЫ ГИБКОСТИ ТОКОПРОВОДЯЩИХ ЖИЛ Классы гибкости № п/п Сечени е, мм 2 Стационарная прокладка Нестационарная прокладка 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 10 16 25 35 50 70 95 120 150 185 240 300 400 500 625 800 2 3 4 5 6 1 1 7 7 7 19 19 37 37 37 61 61 7 7 19 19 19 37 37 37 61 61 127 19 19 27 37 37 61 61 91 – – – 49 49 49 98 144 189 266 330 420 518 672 854 – – 80 224 196 189 266 361 608 756 925 1221 1525 2013 1769 – – 324 513 783 1107 402 999 1332 1702 2109 2590 3360 1270 – –
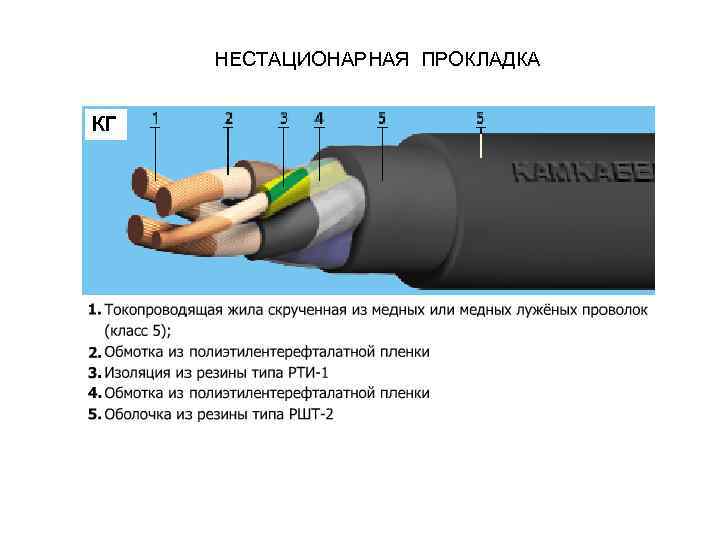
НЕСТАЦИОНАРНАЯ ПРОКЛАДКА
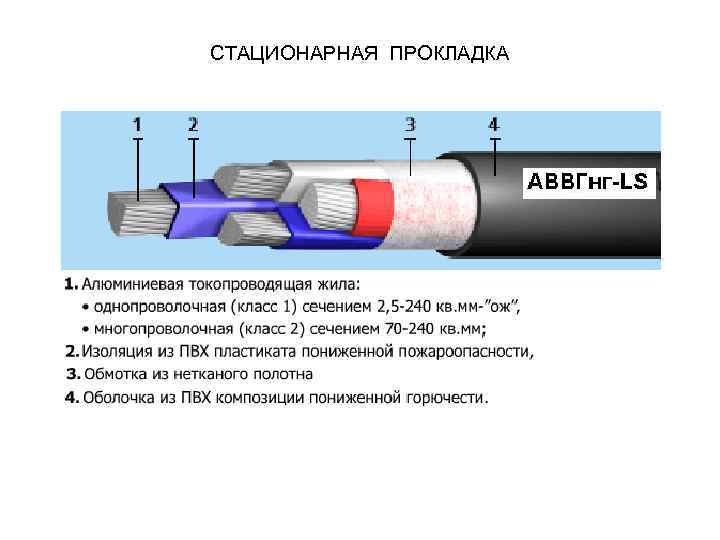
СТАЦИОНАРНАЯ ПРОКЛАДКА
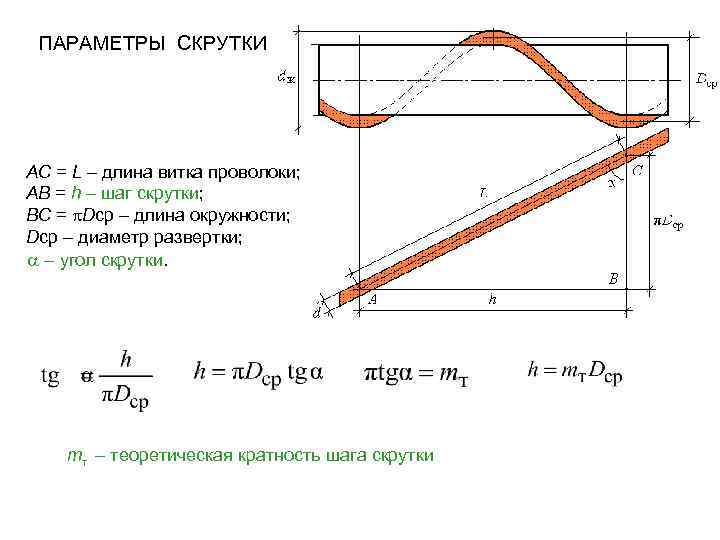
ПАРАМЕТРЫ СКРУТКИ AC = L – длина витка проволоки; AB = h – шаг скрутки; BC = Dср – длина окружности; Dср – диаметр развертки; – угол скрутки. mт – теоретическая кратность шага скрутки

Коэффициент укрутки

Число проволок в повиве Разделим 2 d на d, получим число, на которое проволок в каждом последующем. повиве больше: Следовательно, в каждом следующем повиве на 6, 28 проволоки больше. Учитывая, что количество проволок должно быть целым числом, округляем его в меньшую сторону – до 6 проволок, т. е. между проволоками возникнет зазор. Увеличение числа проволок на 6 в каждом последующем повиве является основным признаком правильной скрутки.

Критический коэффициент укрутки Найдем величину коэффициента укрутки ky, при котором проволоки в повиве будут соприкасаться. Отношение – это число проволок, на которое в каждом следующем повиве больше. Зазор между проволоками будет отсутствовать, если выполняется условие ky = 1, 047 – критический коэффициент укрутки mт ≈ 10

Практическая кратность шага скрутки На производстве удобно измерять диаметр жилы dж, а не Dср, по этой причине применяется практическая кратность шага скрутки

КОНСТРУКЦИИ ТОКОПРОВОДЯЩИХ ЖИЛ 1. Одна проволока в центре. Система скрутки 1 + 6 + 12 + 18 +… Диаметр первого повива – d, второго – 3 d, третьего – 5 d и т. д. , такой ряд соответствует формуле для диаметра жилы где n – число повивов; d – диаметр проволоки. Определим общее число проволок, используя формулы арифметической прогрессии: где N – общее число проволок; a 1 – первый член прогрессии; an – последний член прогрессии; a – разность прогрессии; n – число членов прогрессии.

Для системы скрутки 1 + 6 + 12 + 18 +… применить формулы арифметической прогрессии можно только начиная со второго повива, так как первый повив отличается от второго на 5 проволок (это исключение из правила). В последнем повиве число проволок Общее число проволок в жиле . Эта формула получена без учета центральной проволоки. Запишем эту формулу с учетом центральной проволоки: Коэффициент заполнения жилы:
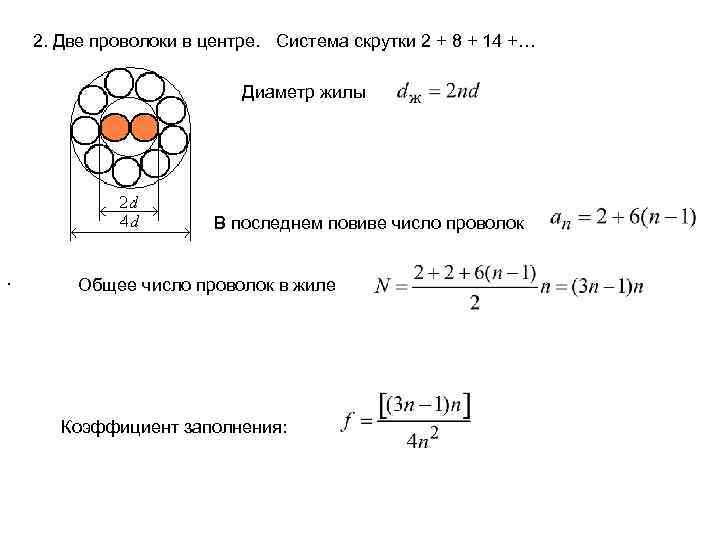
2. Две проволоки в центре. Система скрутки 2 + 8 + 14 +… Диаметр жилы В последнем повиве число проволок. Общее число проволок в жиле Коэффициент заполнения:
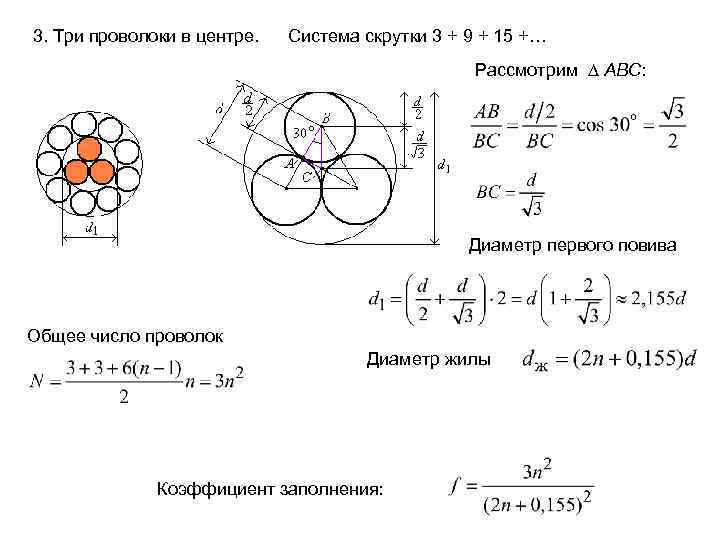
3. Три проволоки в центре. Система скрутки 3 + 9 + 15 +… Рассмотрим ABC: Диаметр первого повива Общее число проволок Диаметр жилы Коэффициент заполнения:
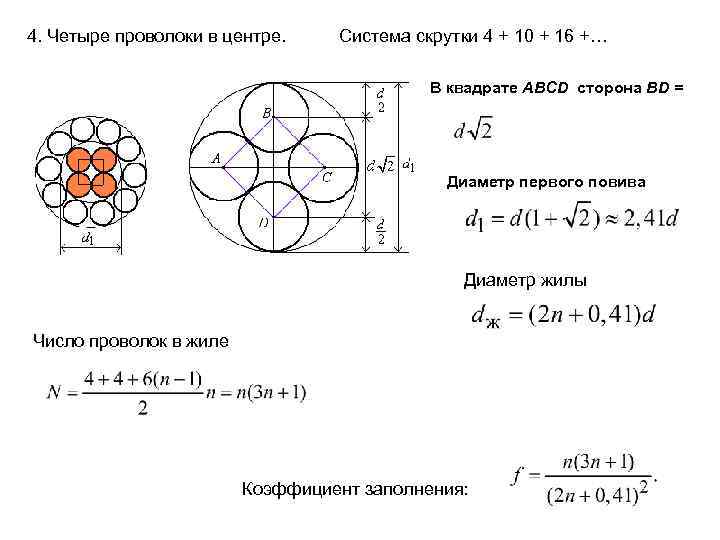
4. Четыре проволоки в центре. Система скрутки 4 + 10 + 16 +… В квадрате ABCD сторона BD = Диаметр первого повива Диаметр жилы Число проволок в жиле Коэффициент заполнения:
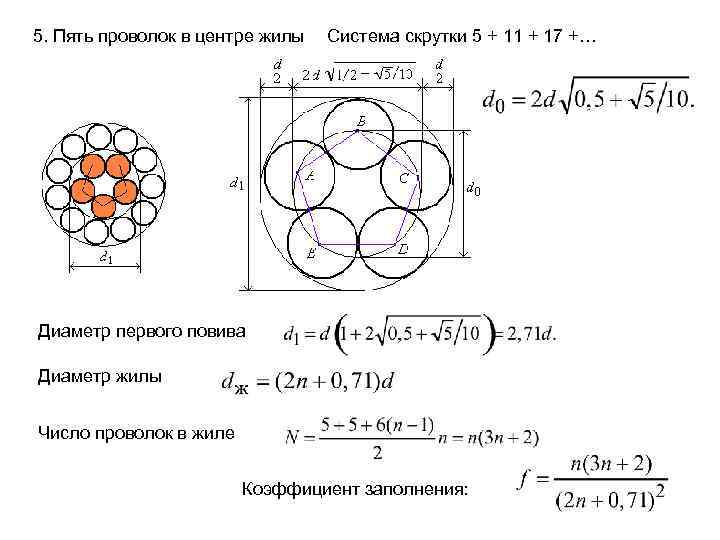
5. Пять проволок в центре жилы Система скрутки 5 + 11 + 17 +… Диаметр первого повива Диаметр жилы Число проволок в жиле Коэффициент заполнения:
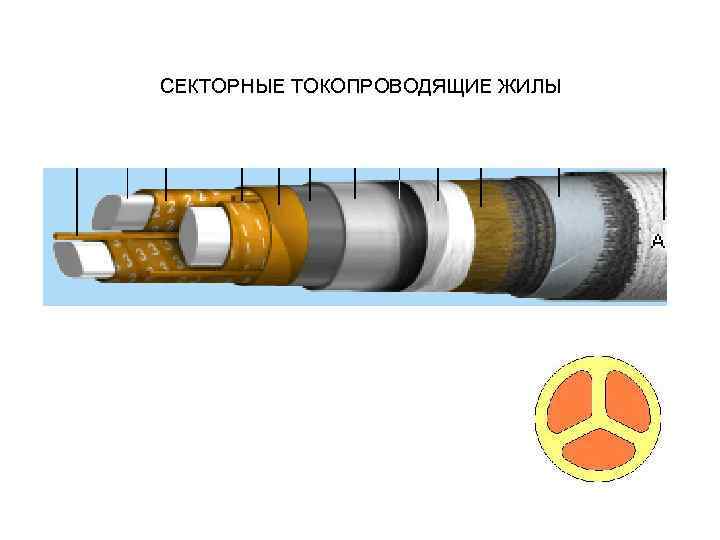
СЕКТОРНЫЕ ТОКОПРОВОДЯЩИЕ ЖИЛЫ
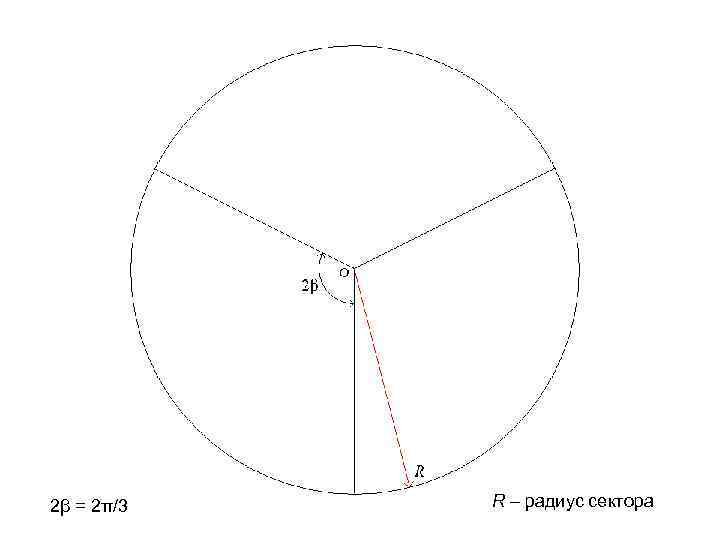
2β = 2π/3 R – радиус сектора
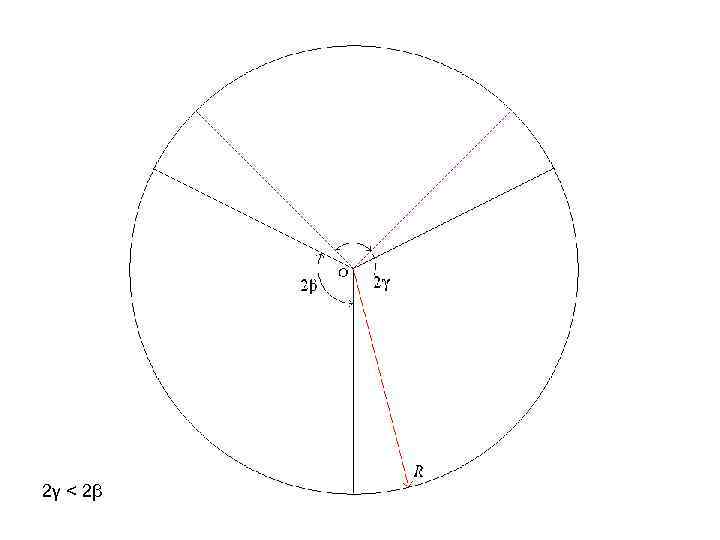
2γ < 2β
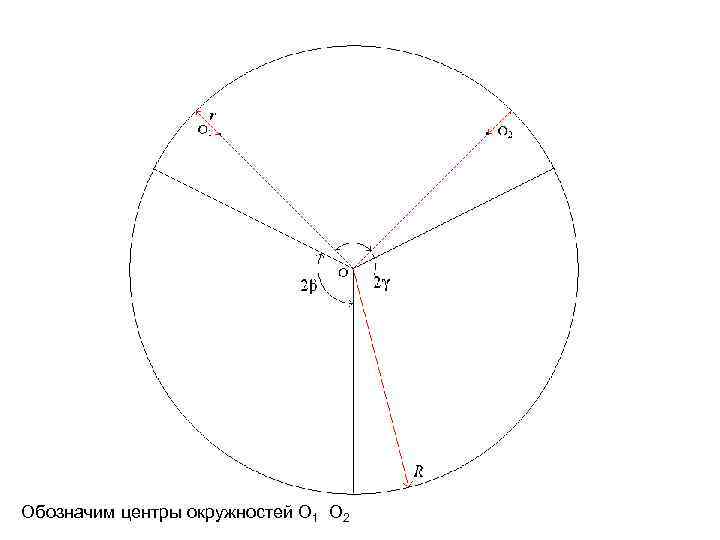
Обозначим центры окружностей О 1 О 2
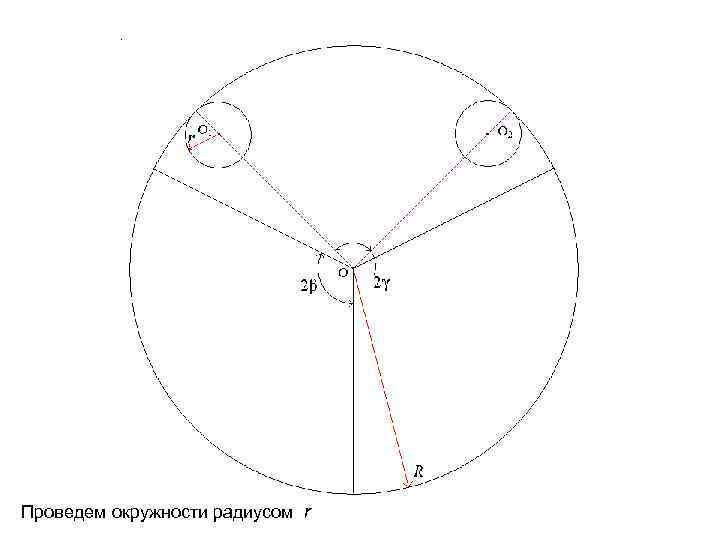
Проведем окружности радиусом r
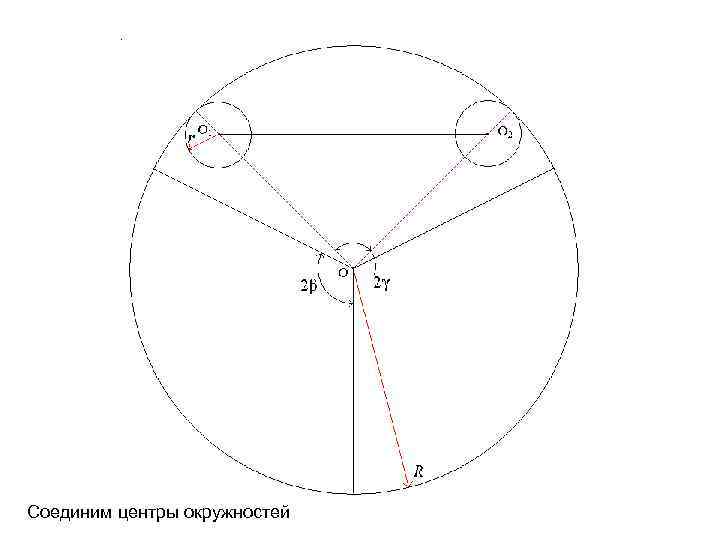
Соединим центры окружностей
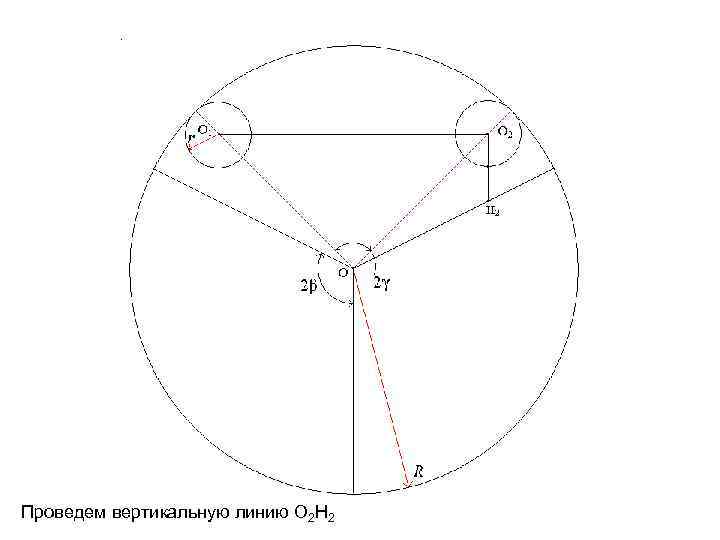
Проведем вертикальную линию O 2 H 2
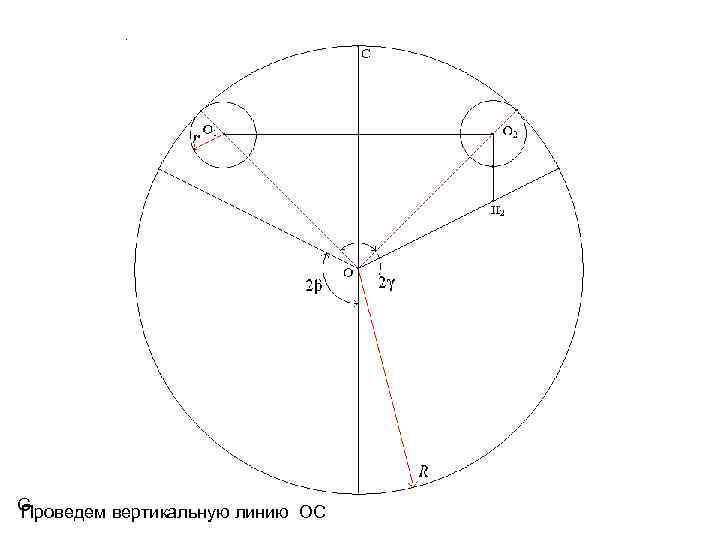
G Проведем вертикальную линию OC
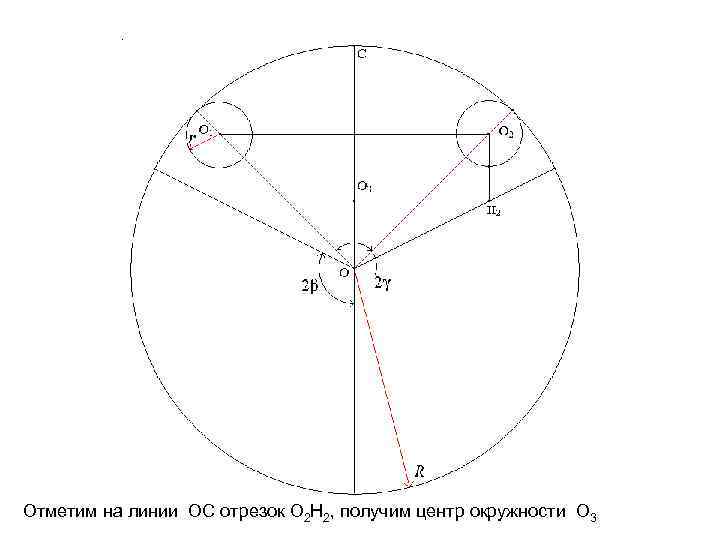
Отметим на линии OC отрезок O 2 H 2, получим центр окружности O 3
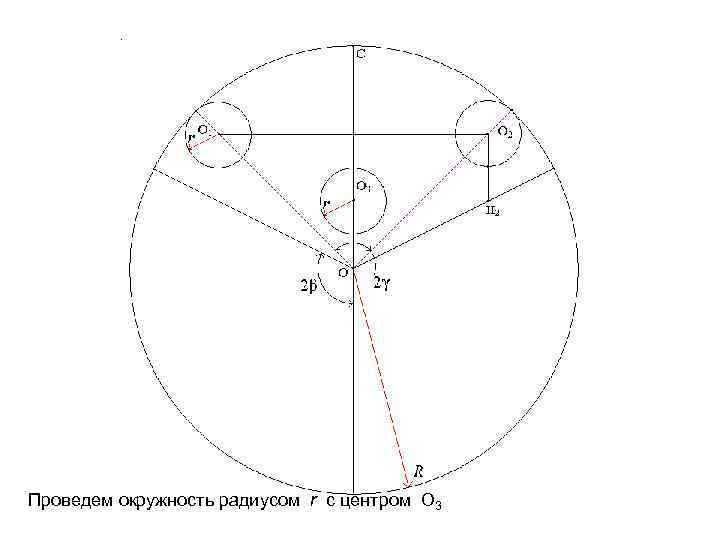
Проведем окружность радиусом r с центром O 3
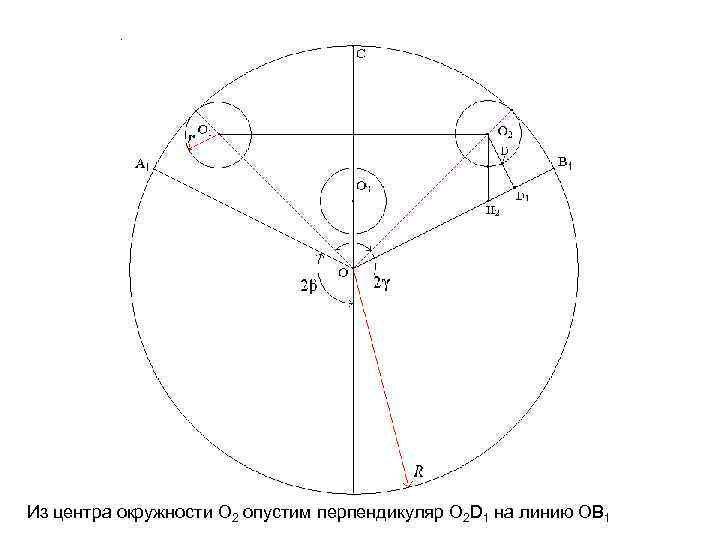
Из центра окружности O 2 опустим перпендикуляр О 2 D 1 на линию OB 1
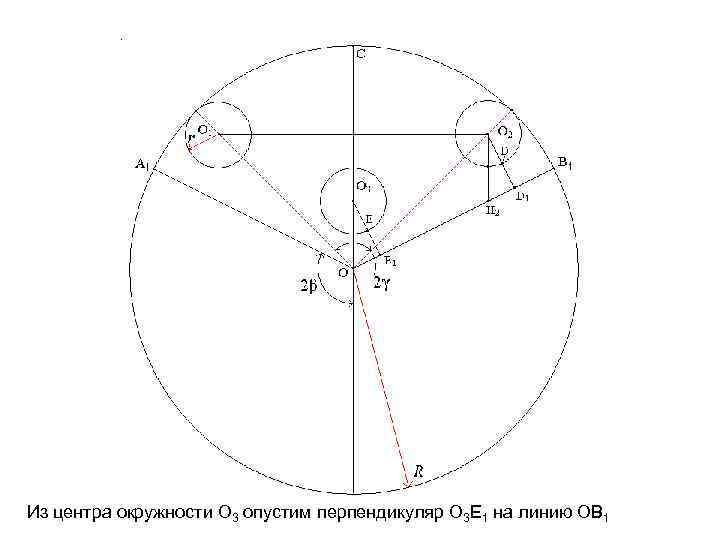
Из центра окружности O 3 опустим перпендикуляр О 3 E 1 на линию OB 1
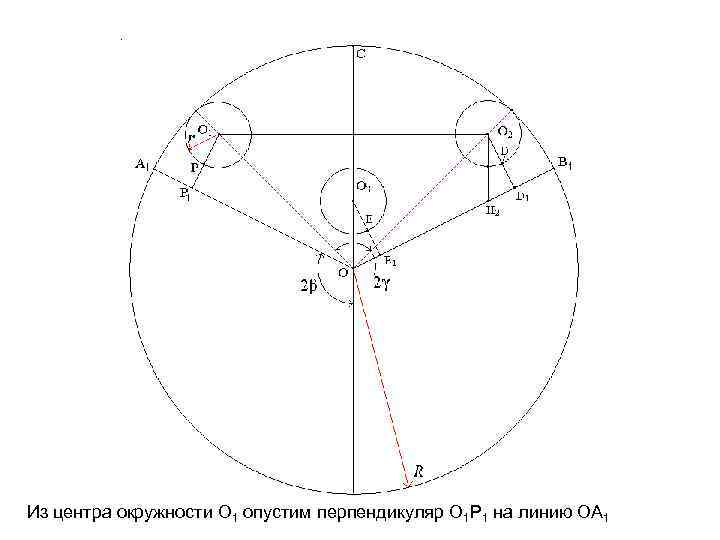
Из центра окружности O 1 опустим перпендикуляр О 1 P 1 на линию OA 1
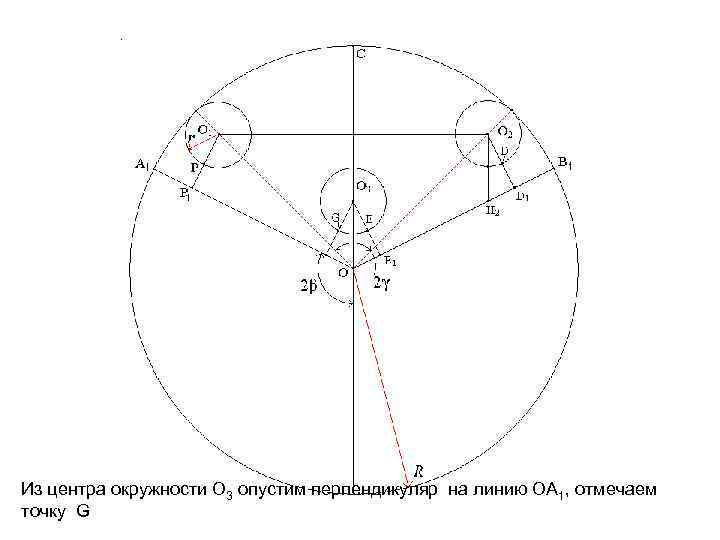
Из центра окружности O 3 опустим перпендикуляр на линию OA 1, отмечаем точку G
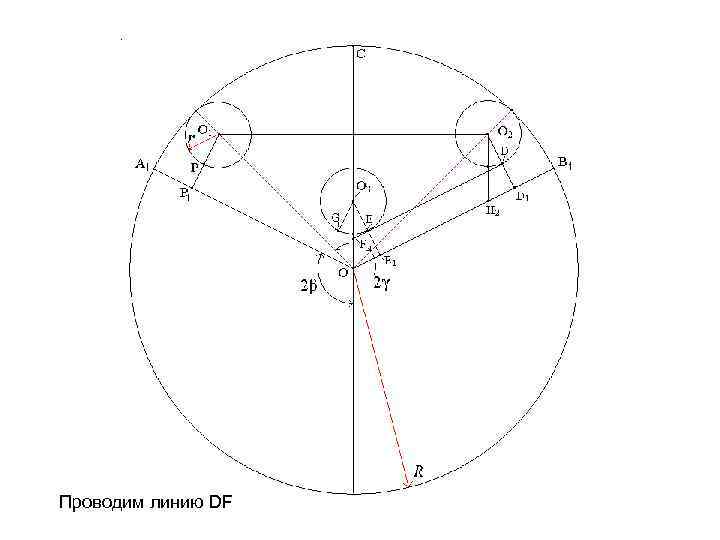
Проводим линию DF
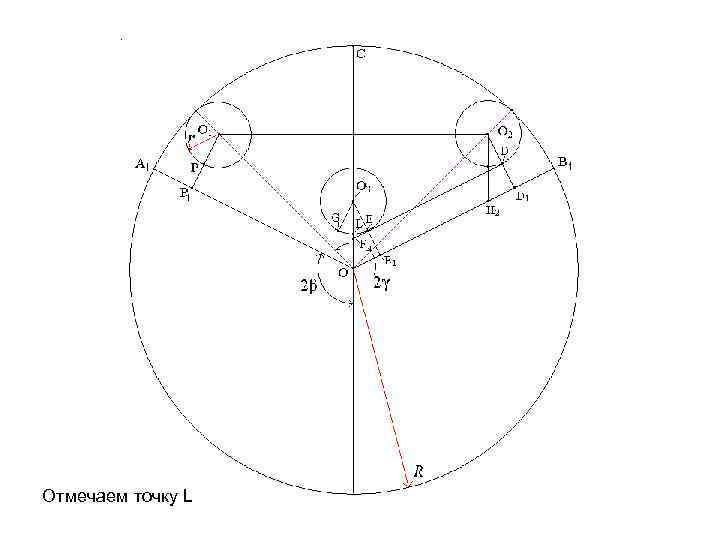
Отмечаем точку L
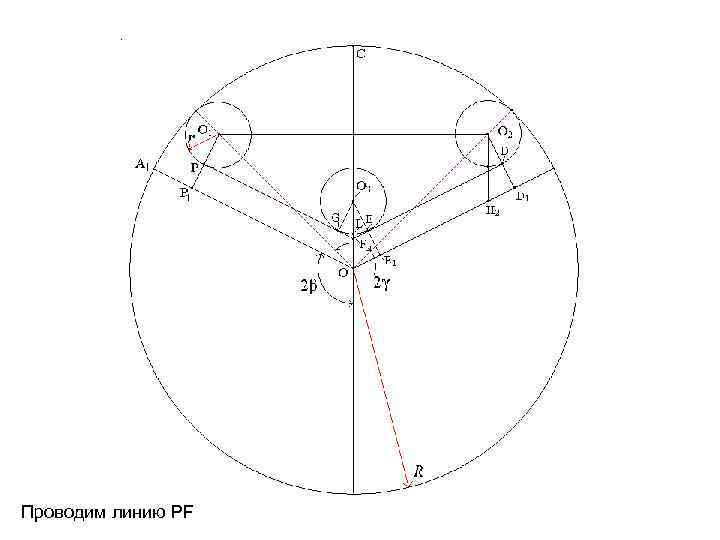
Проводим линию PF
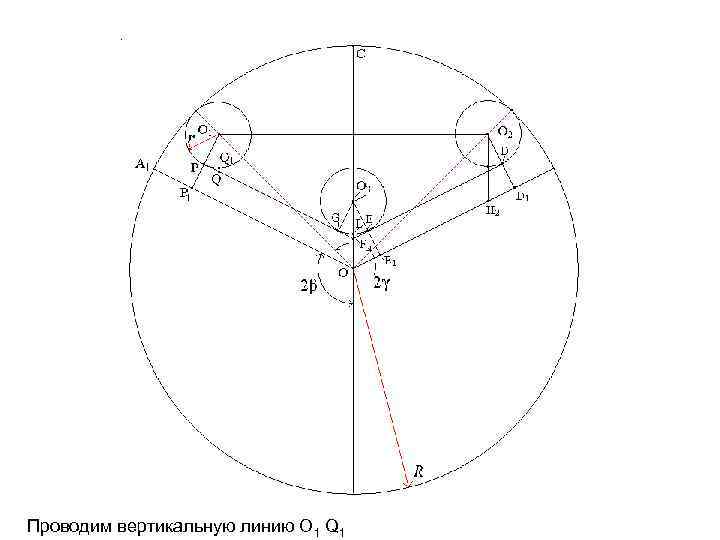
Проводим вертикальную линию О 1 Q 1
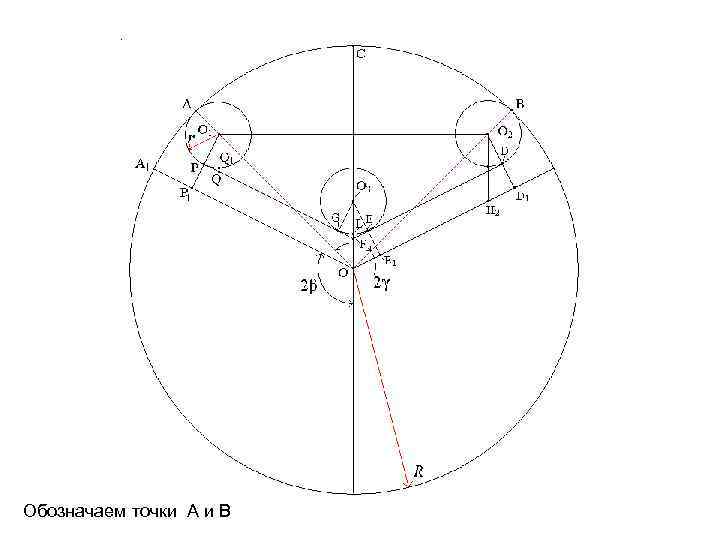
Обозначаем точки A и B
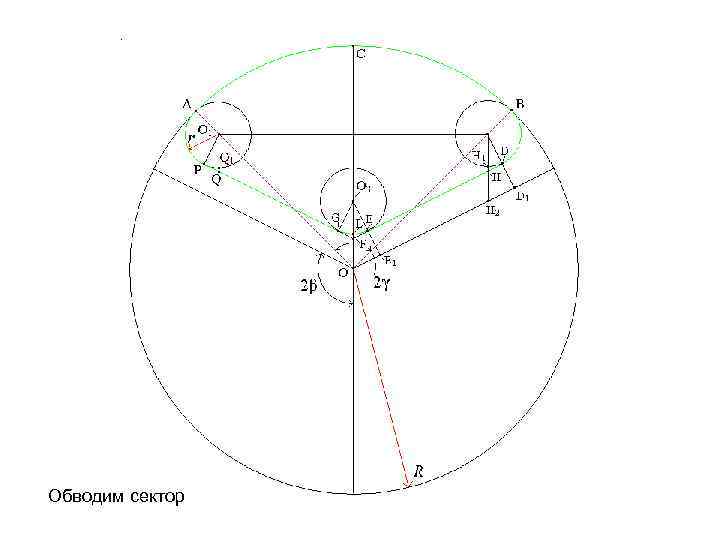
Обводим сектор
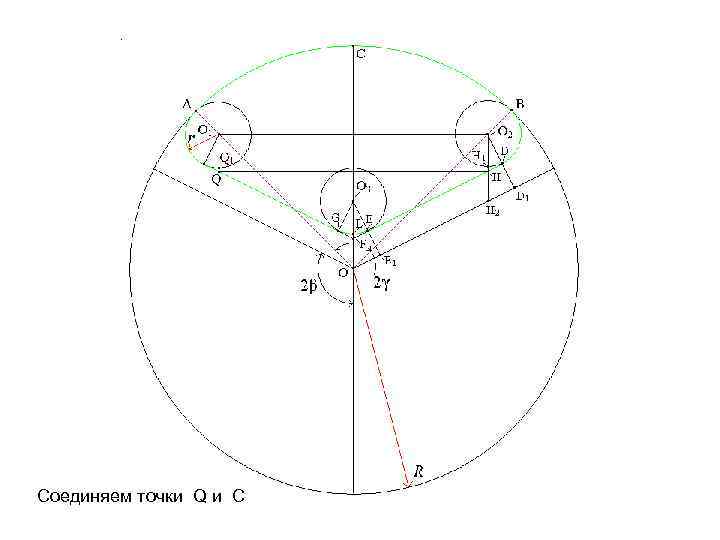
Соединяем точки Q и C
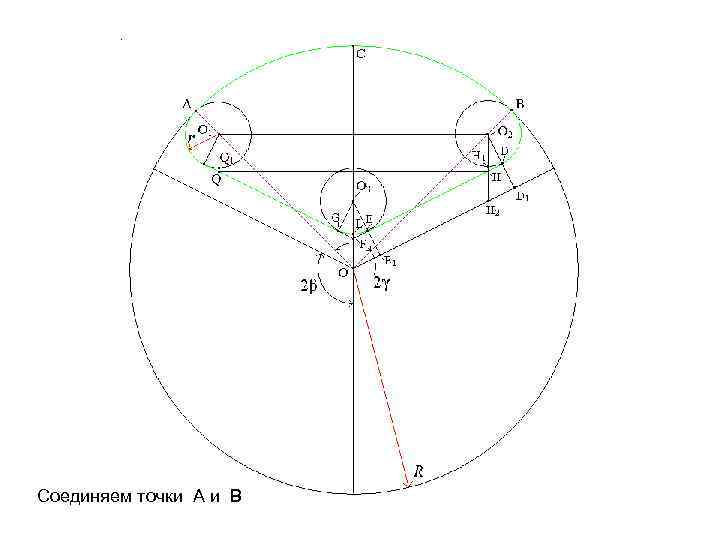
Соединяем точки A и B
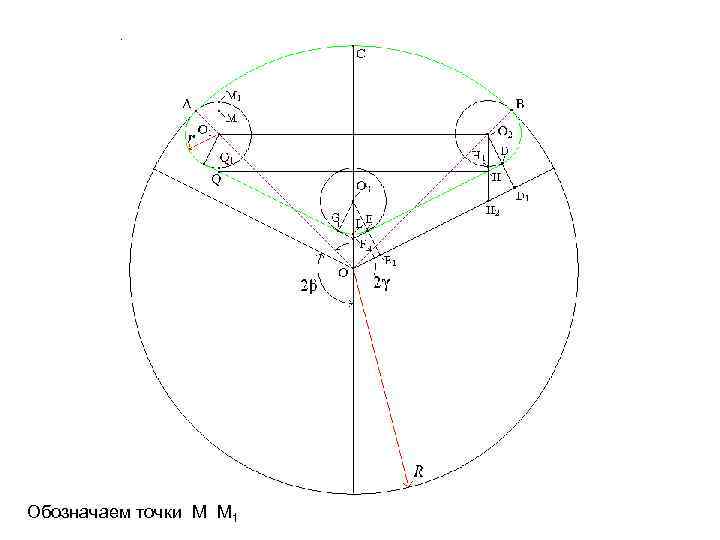
Обозначаем точки M M 1
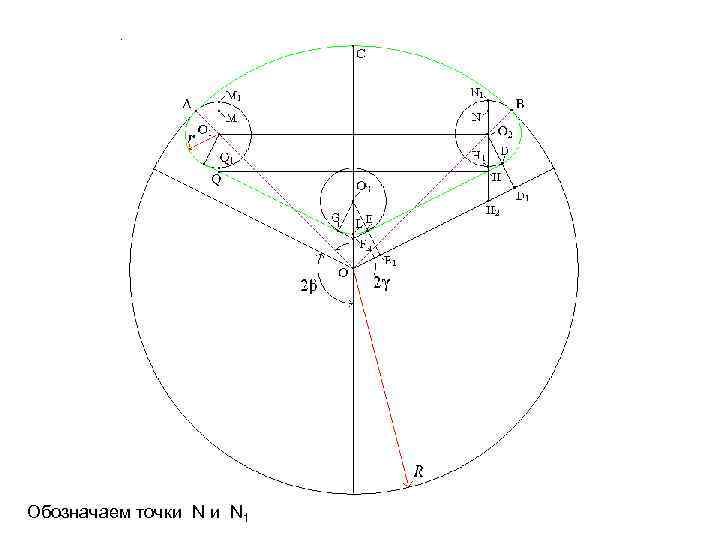
Обозначаем точки N 1
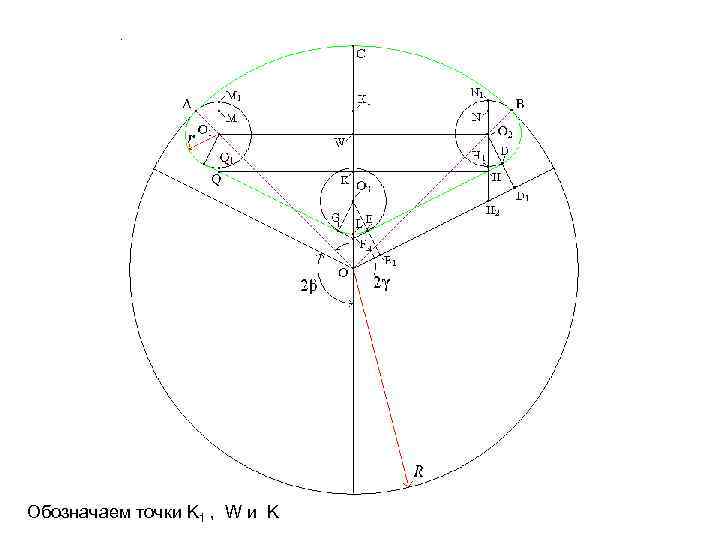
Обозначаем точки K 1 , W и K
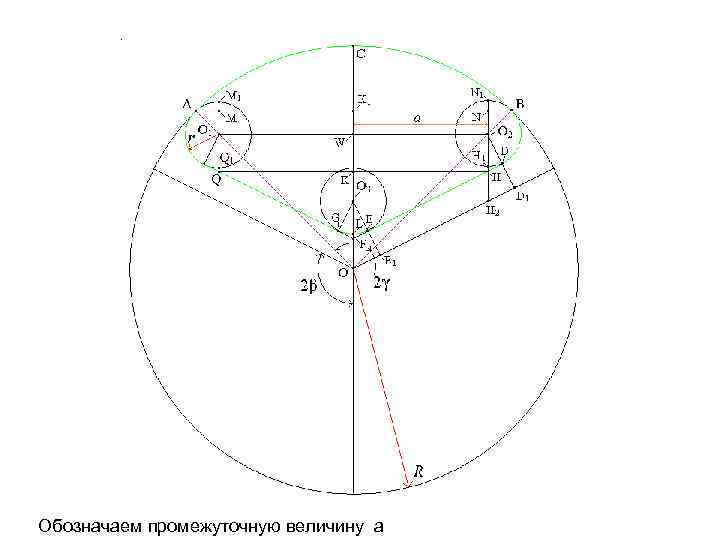
Обозначаем промежуточную величину а
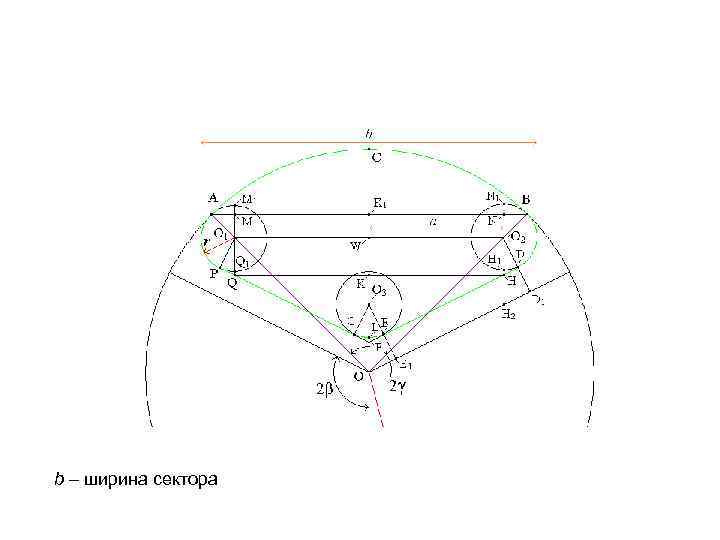
b – ширина сектора
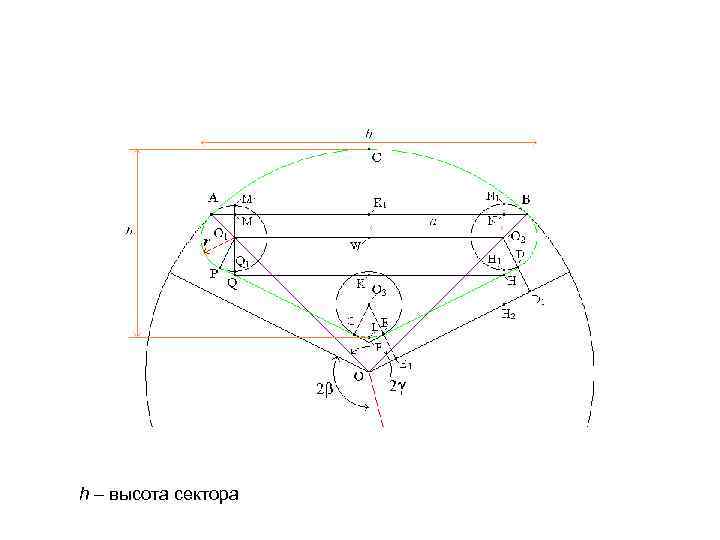
h – высота сектора
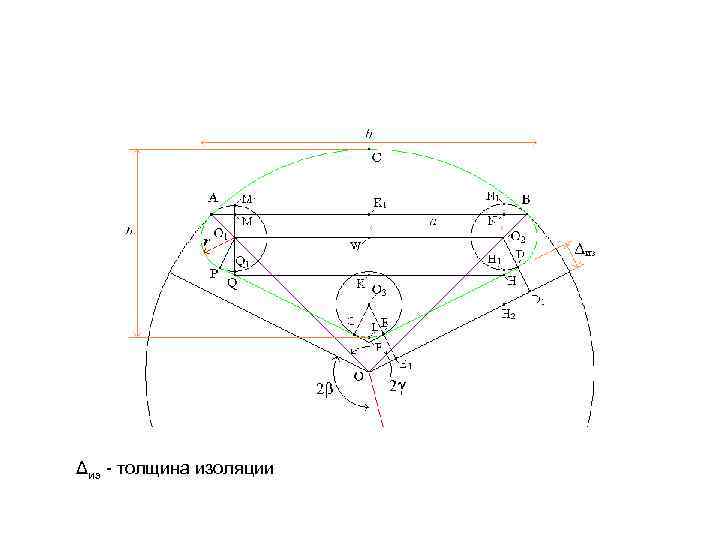
Δиз - толщина изоляции
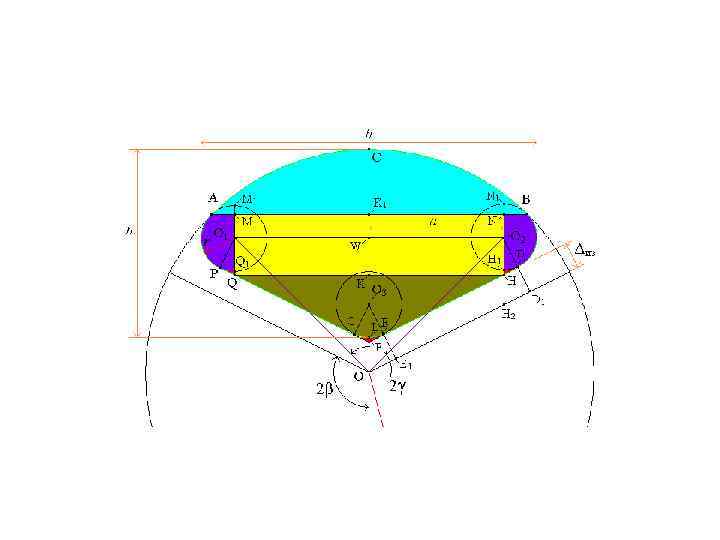
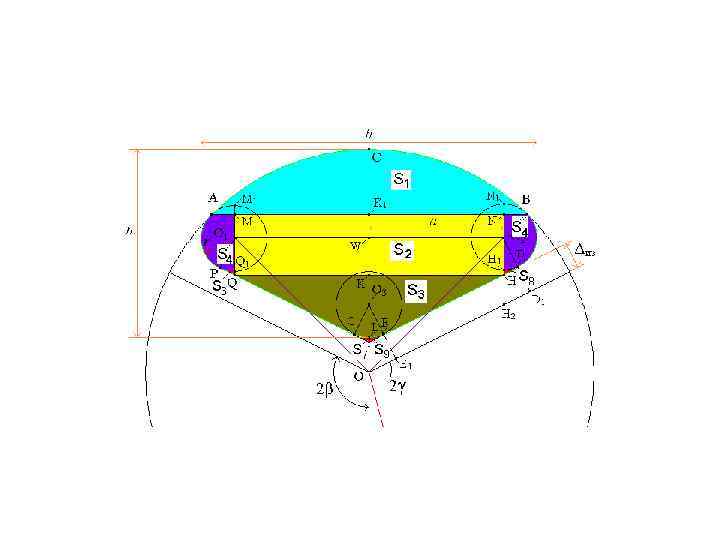

Площадь сегмента S 1 (ABC) равна разности площадей сектора OACB и треугольника OAB Рассмотрим отдельно треугольник OAB, выразим его площадь через известные компоненты:

Площадь прямоугольника QMNH Из треугольника O 2 NB находим NO 2 = rcos ,

Найдем площадь фигуры QHELG: где площадь треугольника. Из отношения выразим KF:
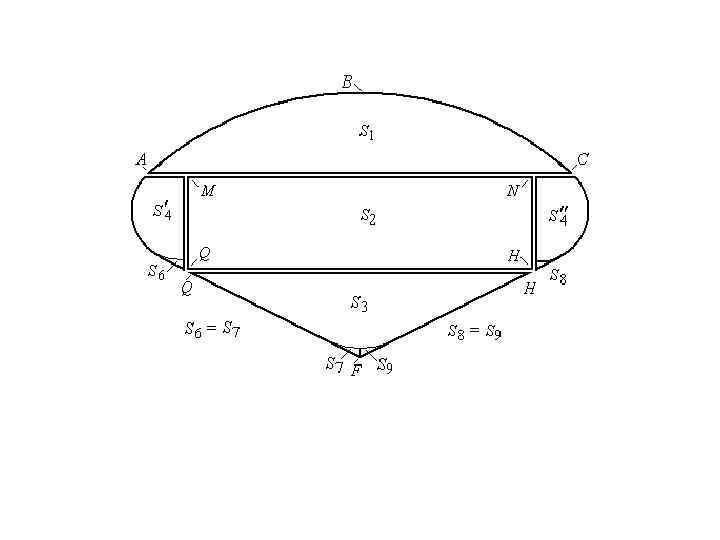

. Площадь S 5 – площадь сегмента, который подобен сегменту ABC, следовательно: S 4 = r 2 – S 5 + S 6 + S 8,

Общая площадь секторной токопроводящей жилы (S = S 1 + S 2 + S 3 + S 4) Учитывая, что S 6 = S 7 и S 8 = S 9, получим

В треугольнике OWO 2 сторона OO 2 равна R – r, следовательно: Ширина сектора Из треугольника OO 2 D 1 имеем

Высота сектора h: CL= OC – OO 3 + O 3 L, где OC = R, O 3 L = r. Принимая во внимание, что OO 3 = O 2 H 2 и O 2 D 1 = r + из, из треугольника O 2 H 2 D 1 найдем: O 2 H 2 = OO 3 = (r + из)/sin. Окончательно имеем

Порядок расчета секторной жилы: 1. Задаем площадь поперечного сечения токопроводящей жилы S, радиус закругления сектора r и толщину изоляции из. 2. Задаем приближенное значение 3. Вычисляем угол . 4. Определяем a. 5. Вычисляем сечение Sр по формуле. Сравниваем рассчитанное значение Sр с заданным S. В том случае, если рассчитанное значение Sр меньше заданного S, произвольно увеличиваем R на некоторую небольшую величину и повторяем расчет с пункта 3 до тех пор, пока Sр не будет равно S с наперед заданной точностью. 6. Вычисляем высоту h и ширину b сектора.

). Введем прямоугольную систему координат x, y, z (рис. 2. 1) и обозначим вектор электрического смещения в некоторой точке a(x, y, z) через

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В КАБЕЛЕ Для расчета электрического поля в кабеле применим теорему Остроградского – Гаусса, которая в интегральной форме имеет вид т. е. поток (N) вектора электрического смещения (D) через замкнутую поверхность (S) равен сумме зарядов (q), расположенных в объеме, ограниченном этой поверхностью.

Теорема Остроградского – Гаусса связывает значения вектора электрического смещения в точках некоторой замкнутой поверхности с величиной заряда, находящегося внутри объема, ограниченного этой поверхностью. Можно придать этой теореме такую форму, чтобы в нее входили величины, относящиеся к одной и той же точке поля. Введем прямоугольную систему координат x, y, z и обозначим вектор электрического смещения в некоторой точке a(x, y, z) через D(Dx, Dy, Dz).

Поток через плоскость dydz (заштрихована), проходящую через точку a, есть – (знак минус поставлен потому, что внешняя нормаль к плоскости dydz и положительное направление вектора Dx составляют угол = и cos = – 1). Поток через параллельную ей грань, смещенную вдоль оси x на dx, есть
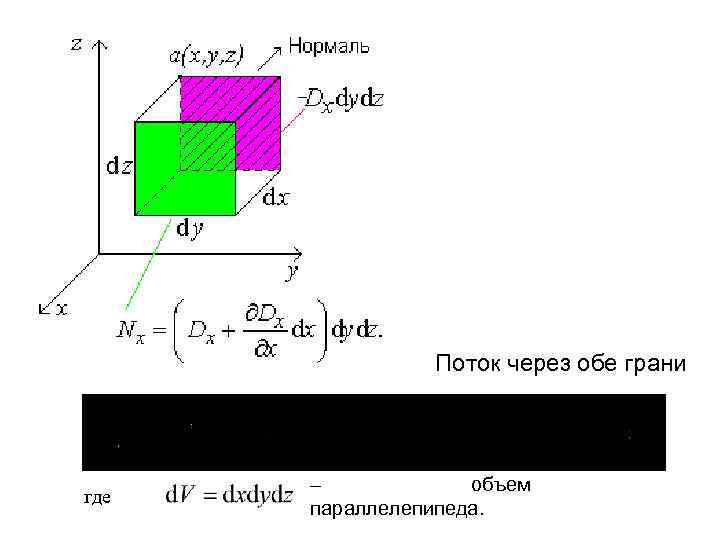
Поток через обе грани где – объем параллелепипеда.

Вычисляя аналогичным образом потоки через другие две пары граней и складывая их, мы получаем полный поток через всю поверхность параллелепипеда:

Если в рассматриваемом пространстве имеется распределенный в объеме заряд с объемной плотностью , то величина заряда, содержащегося в объеме параллелепипеда, равна d. V. Приравняв поток вектора D к заряду получим или Это соотношение, выражающее теорему Остроградского – Гаусса в дифференциальной форме, носит название уравнения Пуассона – div D =

Используя выражение , получим

Если диэлектрическая проницаемость не зависит от координа , то уравнение Пуассона примет вид

Нам предстоит решать общую задачу электростатики, т. е. по заданной форме проводников, их расположению и значению их потенциалов находить значение потенциалов в любой точке между проводниками. Математически эта задача сводится к следующему. Составляющие напряженности поля E по координатам можно выразить через потенциал: ил и , ,
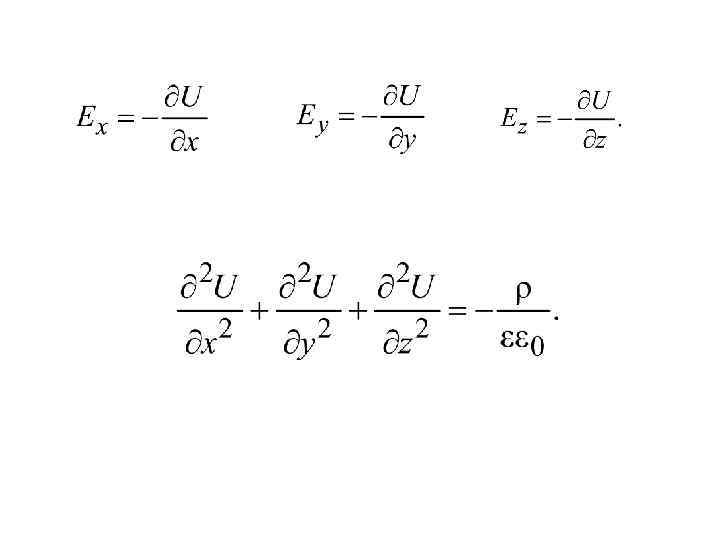

В изоляции кабелей нет свободных зарядов, поэтому или Это уравнение называется уравнением Лапласа.
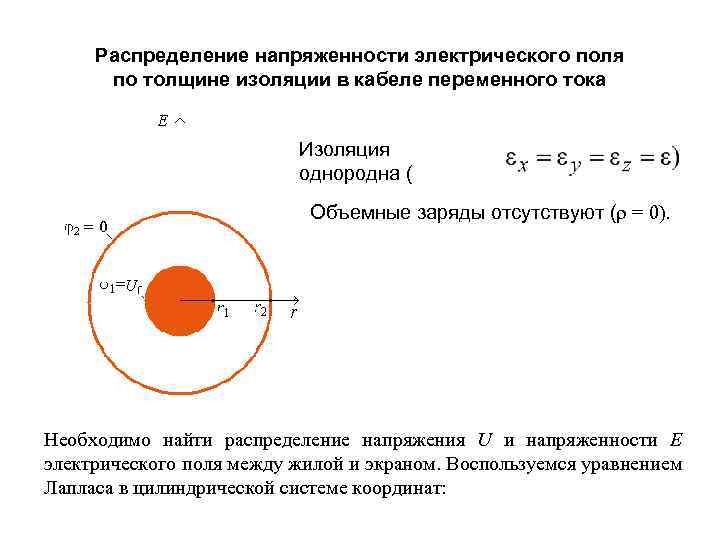
Распределение напряженности электрического поля по толщине изоляции в кабеле переменного тока Изоляция однородна ( Объемные заряды отсутствуют ( = 0). , Необходимо найти распределение напряжения U и напряженности E электрического поля между жилой и экраном. Воспользуемся уравнением Лапласа в цилиндрической системе координат:

Уравнение Лапласа в цилиндрической системе координат:
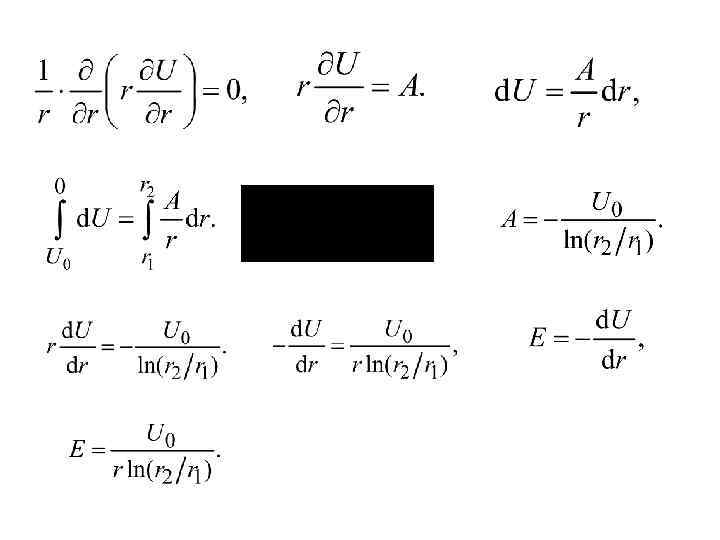
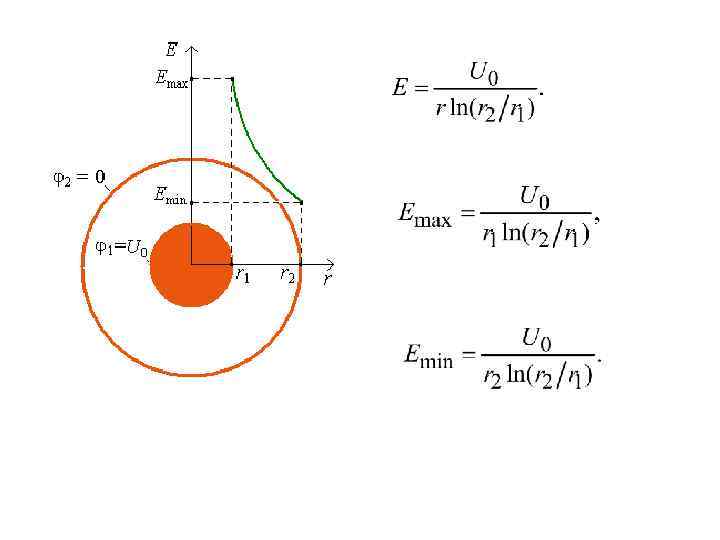

Распределение напряжения по толщине изоляции в кабеле переменного тока
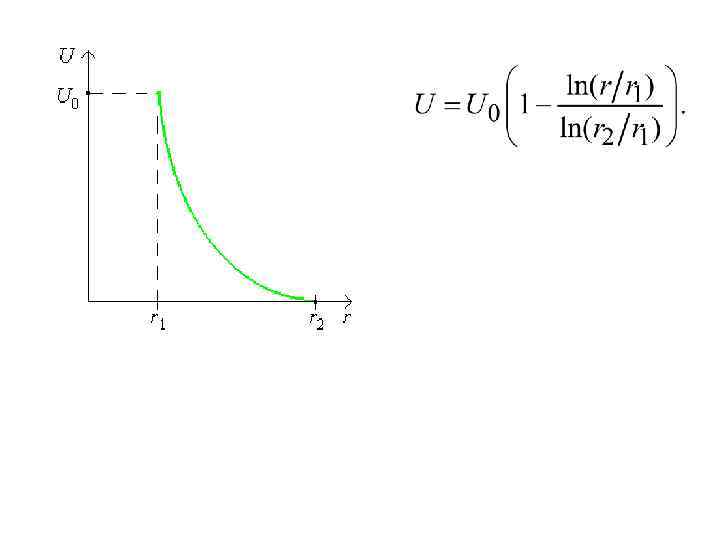

Расчет толщины изоляции кабеля переменного тока с круглой жилой и цилиндрическим экраном Определим, при каком соотношении радиусов r 2/r 1 напряженность электрического поля на токопроводящей жиле Eж будет наименьшей. Для этого необходимо взять производную по r 2/r 1 и приравнять ее к нулю. Обозначим r 2/r 1 через x и Emax через Eж – напряженность электрического поля на жиле. Умножим на r 2 числитель и знаменатель уравнения

Заменим отношение радиусов r 2/r 1 на x: Продифференцируем выражение по x и приравняем его к нулю для нахождения минимума функции: , x = e 1 , r 2/r 1 = e.
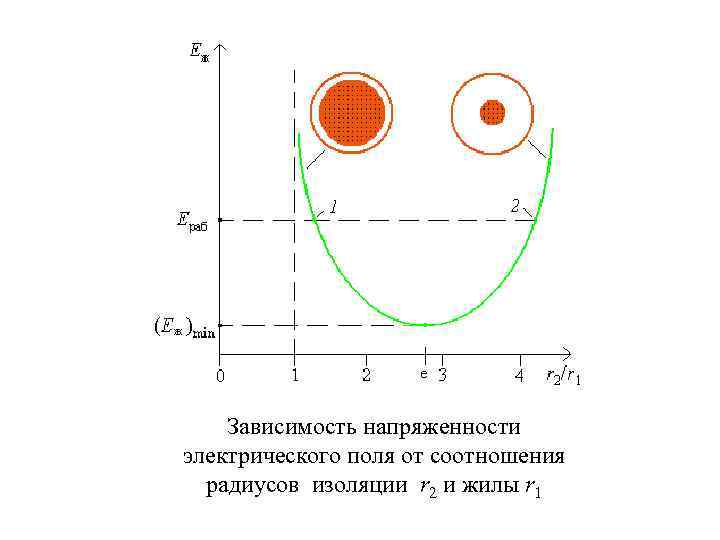
Зависимость напряженности электрического поля от соотношения радиусов изоляции r 2 и жилы r 1

Коэффициент использования изоляции – средняя напряженность электрического поля. Для соотношения радиусов r 2/r 1 = e получим = 0, 58. Это низкий коэффициент использования изоляции, поэтому соотношение радиусов r 2/r 1 = e применяется редко.
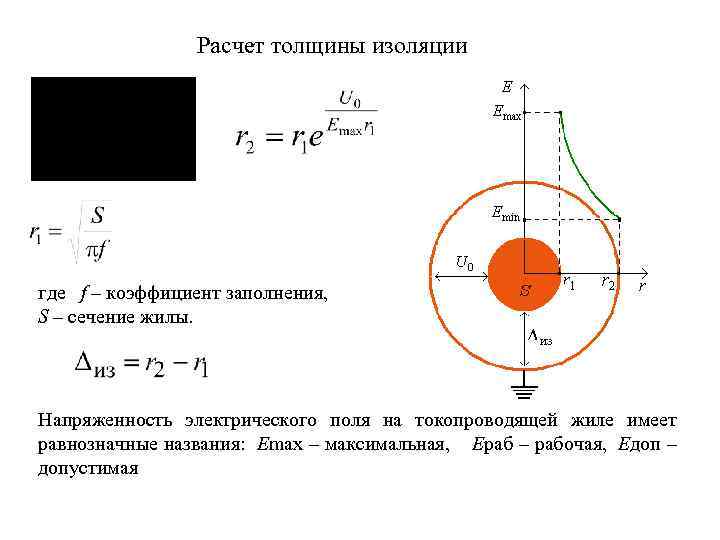
Расчет толщины изоляции где f – коэффициент заполнения, S – сечение жилы. Напряженность электрического поля на токопроводящей жиле имеет равнозначные названия: Emax – максимальная, Eраб – рабочая, Eдоп – допустимая
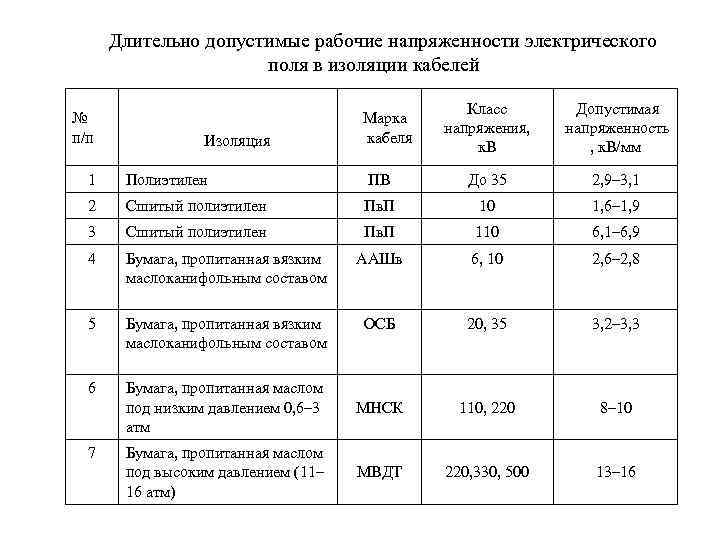
Длительно допустимые рабочие напряженности электрического поля в изоляции кабелей № п/п Изоляция Марка кабеля Класс напряжения, к. В Допустимая напряженность , к. В/мм 1 Полиэтилен ПВ До 35 2, 9– 3, 1 2 Сшитый полиэтилен Пв. П 10 1, 6– 1, 9 3 Сшитый полиэтилен Пв. П 110 6, 1– 6, 9 4 Бумага, пропитанная вязким маслоканифольным составом ААШв 6, 10 2, 6– 2, 8 5 Бумага, пропитанная вязким маслоканифольным составом ОСБ 20, 35 3, 2– 3, 3 6 Бумага, пропитанная маслом под низким давлением 0, 6– 3 атм МНСК 110, 220 8– 10 Бумага, пропитанная маслом под высоким давлением (11– 16 атм) МВДТ 220, 330, 500 13– 16 7
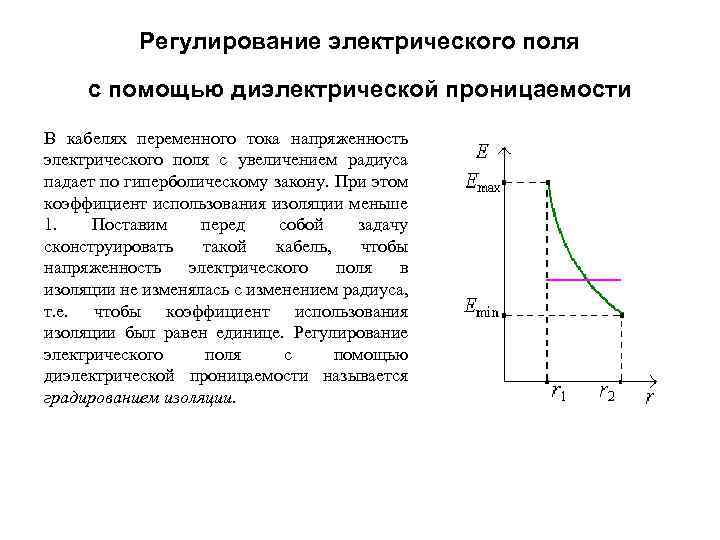
Регулирование электрического поля с помощью диэлектрической проницаемости В кабелях переменного тока напряженность электрического поля с увеличением радиуса падает по гиперболическому закону. При этом коэффициент использования изоляции меньше 1. Поставим перед собой задачу сконструировать такой кабель, чтобы напряженность электрического поля в изоляции не изменялась с изменением радиуса, т. е. чтобы коэффициент использования изоляции был равен единице. Регулирование электрического поля с помощью диэлектрической проницаемости называется градированием изоляции.

Воспользуемся теоремой Остроградского – Гаусса DS = Q. Подставим в уравнение D = 0 E и S = 2 r. L и выразим E:

Интегрируя напряженность Е по радиусу r, получим напряжение ынесем из-под знака интеграла величины, которые не зависят от радиуса: Подставим Q:

После сокращения имеем Выразим напряженность:

В том случае, если произведение r равно постоянной величине а, имеем или
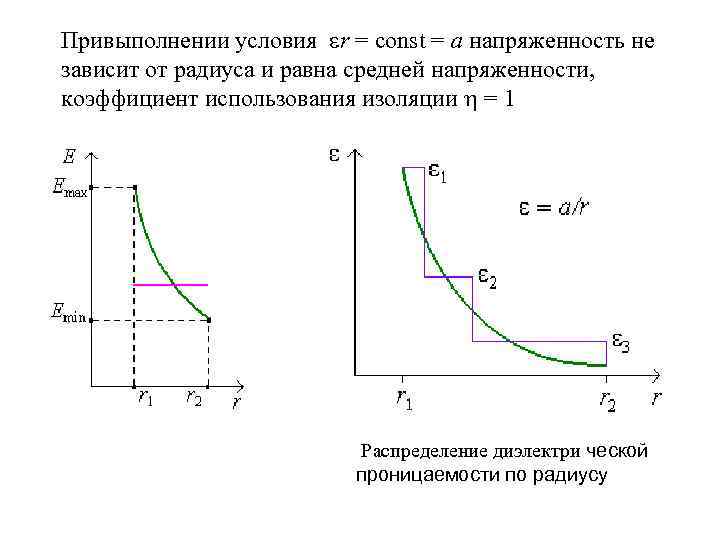
Привыполнении условия r = const = a напряженность не зависит от радиуса и равна средней напряженности, коэффициент использования изоляции = 1 Распределение диэлектри ческой проницаемости по радиусу

Двухслойная изоляция
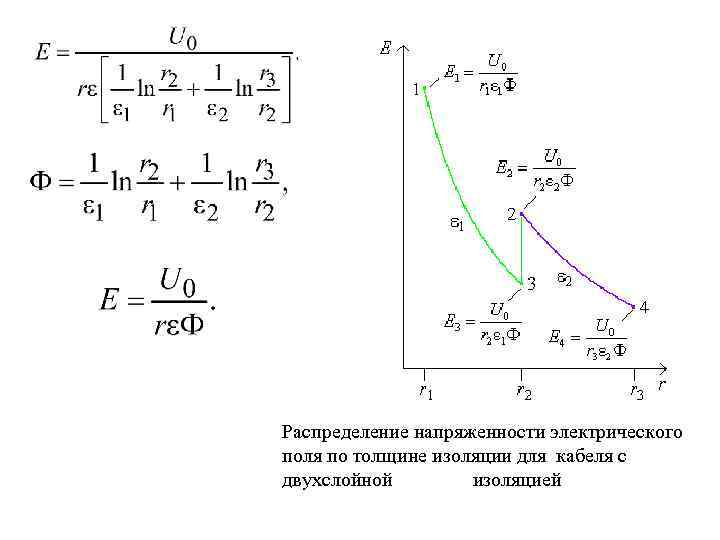
Распределение напряженности электрического поля по толщине изоляции для кабеля с двухслойной изоляцией
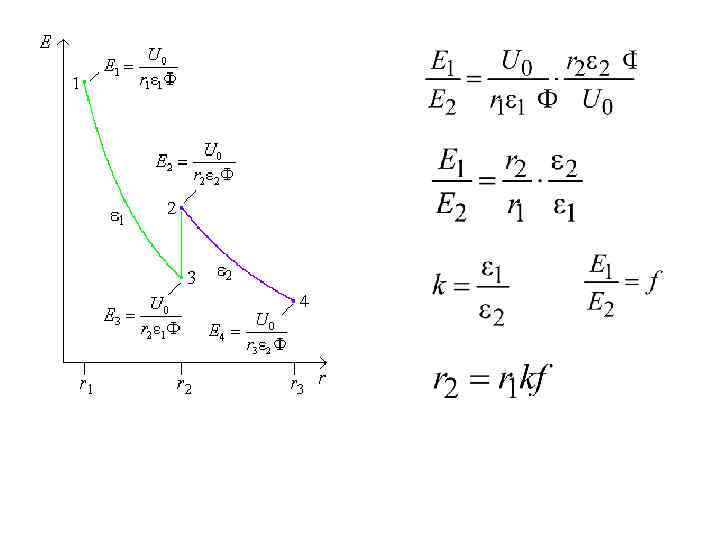

Внесем 1 в квадратные скобки и, используя , а также k = 1/ 2, получим

Выразим радиус r 3, для этого запишем последнюю формулу в следующем виде:
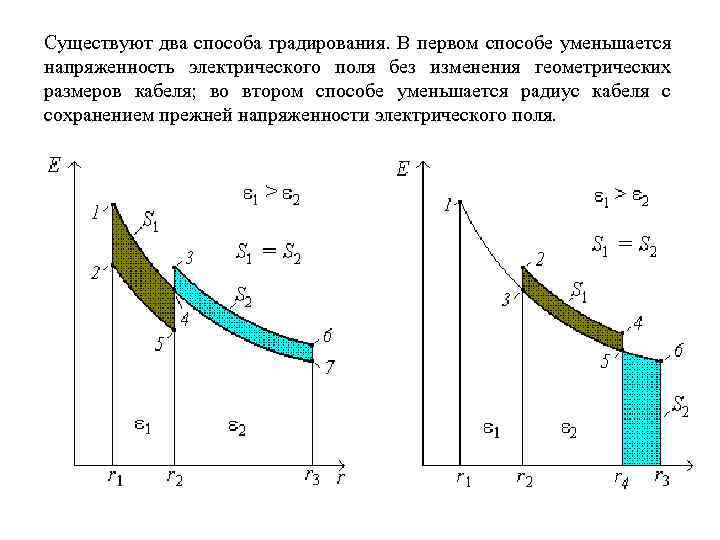
Существуют два способа градирования. В первом способе уменьшается напряженность электрического поля без изменения геометрических размеров кабеля; во втором способе уменьшается радиус кабеля с сохранением прежней напряженности электрического поля.
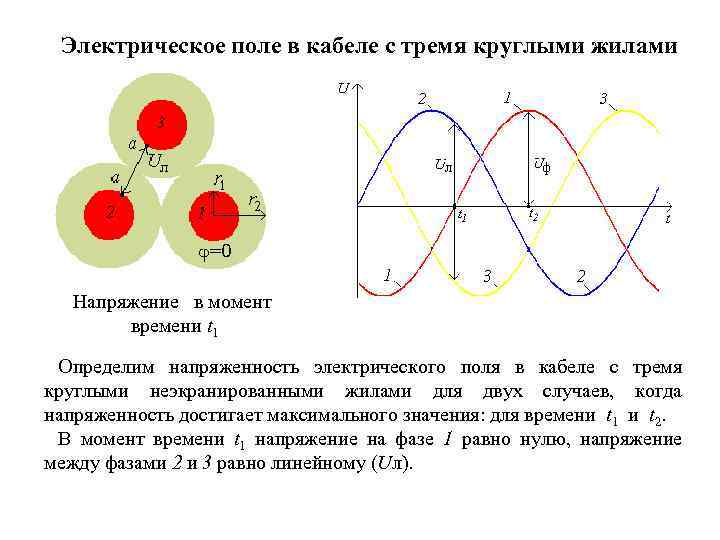
Электрическое поле в кабеле с тремя круглыми жилами Напряжение в момент времени t 1 Определим напряженность электрического поля в кабеле с тремя круглыми неэкранированными жилами для двух случаев, когда напряженность достигает максимального значения: для времени t 1 и t 2. В момент времени t 1 напряжение на фазе 1 равно нулю, напряжение между фазами 2 и 3 равно линейному (Uл).
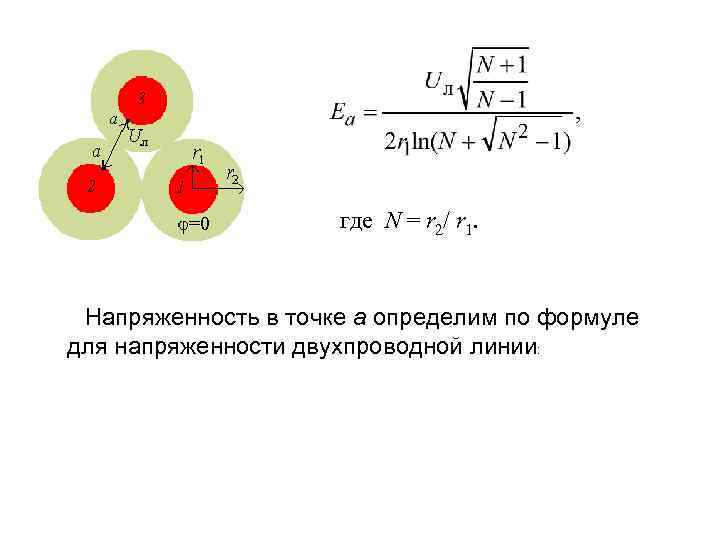
где N = r 2/ r 1. Напряженность в точке а определим по формуле для напряженности двухпроводной линии:
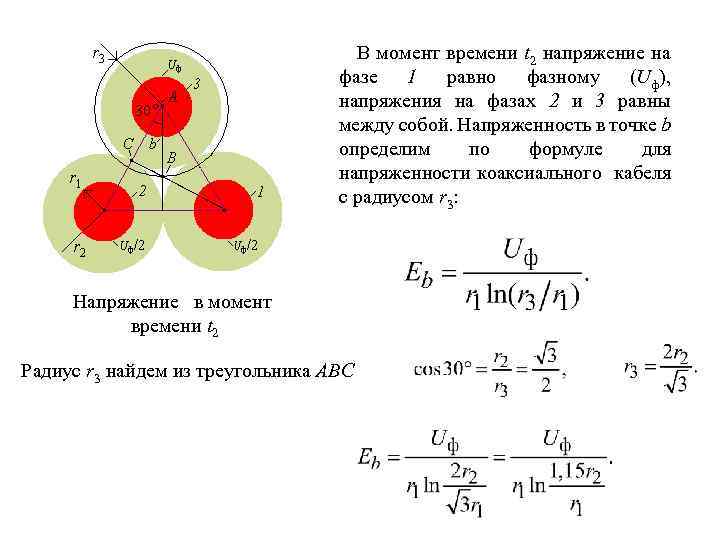
В момент времени t 2 напряжение на фазе 1 равно фазному (Uф), напряжения на фазах 2 и 3 равны между собой. Напряженность в точке b определим по формуле для напряженности коаксиального кабеля с радиусом r 3: Напряжение в момент времени t 2 Радиус r 3 найдем из треугольника ABC
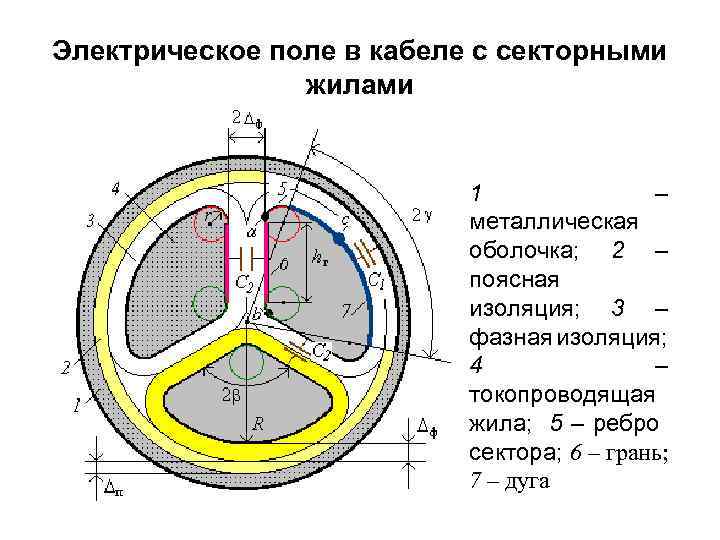
Электрическое поле в кабеле с секторными жилами 1 – металлическая оболочка; 2 – поясная изоляция; 3 – фазная изоляция; 4 – токопроводящая жила; 5 – ребро сектора; 6 – грань; 7 – дуга
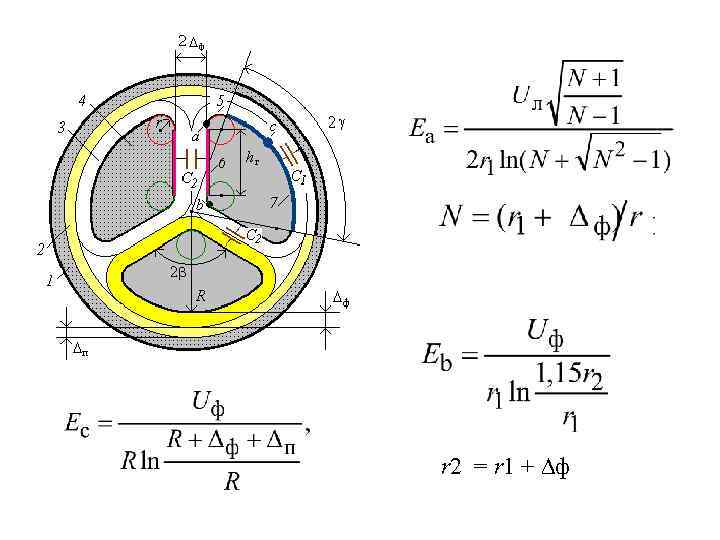
r 2 = r 1 + ф
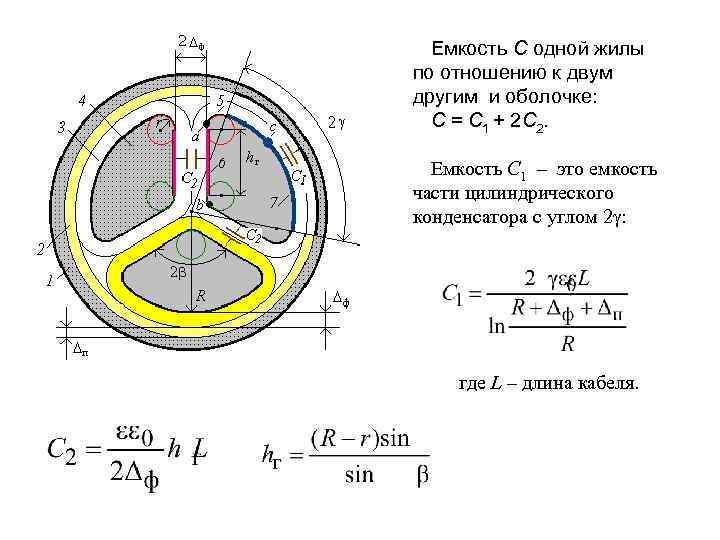
Емкость С одной жилы по отношению к двум другим и оболочке: С = С 1 + 2 С 2. Емкость С 1 – это емкость части цилиндрического конденсатора с углом 2 : где L – длина кабеля.
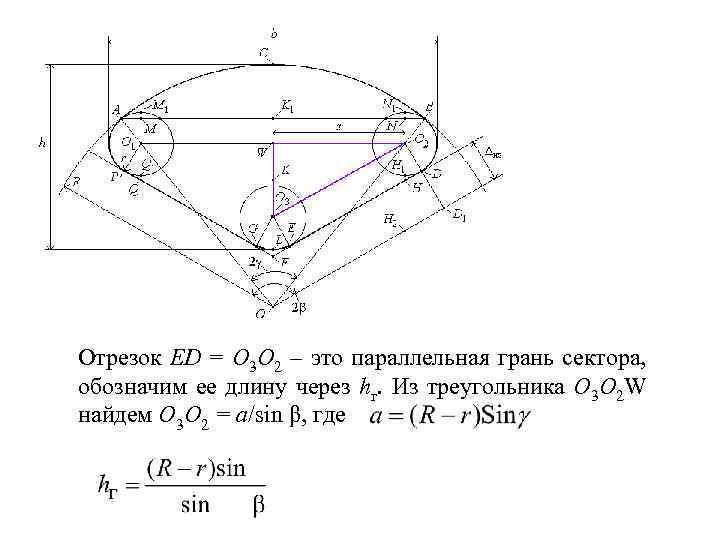
Отрезок ED = O 3 O 2 – это параллельная грань сектора, обозначим ее длину через hг. Из треугольника O 3 O 2 W найдем O 3 O 2 = a/sin β, где
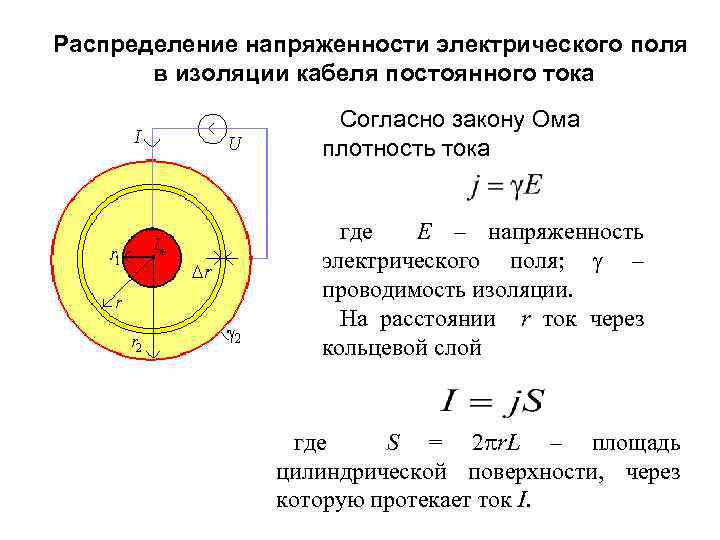
Распределение напряженности электрического поля в изоляции кабеля постоянного тока Согласно закону Ома плотность тока где E – напряженность электрического поля; – проводимость изоляции. На расстоянии r ток через кольцевой слой где S = 2 r. L – площадь цилиндрической поверхности, через которую протекает ток I.

Подставим S в выражение Из закона Ома напряженность поля Интегрируя напряженность от r 1 до r 2, получим напряжение

Удельная проводимость изоляции зависит как от температуры, так и от напряженности электрического поля. Температура и напряженность электрического поля изменяются по радиусу, поэтому оставляем под интегралом:

В изоляции напряженность электрического поля В изоляции у оболочки напряженность электрического поля Разделим E на E 2

Если имеется диэлектрик, проводимость которого зависит от температуры и напряженности электрического поля, то две точки диэлектрика связаны соотношением: где – перепад температур; a – температурный коэффициент удельного объемного сопротивления; k – величина, которая зависит от типа диэлектрика.

Cвяжем проводимость в любой точке изоляции γ с проводимостью γ 2 на радиусе r 2 , т. е. на поверхности изоляции: где E – напряженность электрического поля в любой точке изоляции; E 2 – напряженность электрического поля на радиусе r 2.

Определим перепад температур из теплового закона Ома: или где P – тепловой токопроводящей жилы, сопротивление изоляции. поток, идущий от Sиз – тепловое

Тепловое сопротивление ΔSиз элементарного слоя Δr прямо пропорционально удельному тепловому сопротивлению изоляции σиз, толщине слоя Δr и обратно пропорционально площади поверхности S = 2 r. L: Интегрируя от произвольного радиуса r до r 2, получим зависимость теплового сопротивления изоляции от радиуса относительно r 2:

Подставим Возьмем Подставим и получим

Введем обозначение и преобразование: выполним.

Сделаем некоторые преобразования и получим Введем обозначение .

Возьмем выражение Вычислим отдельно интеграл ,

Подставим интеграл обратно Окончательно имеем.
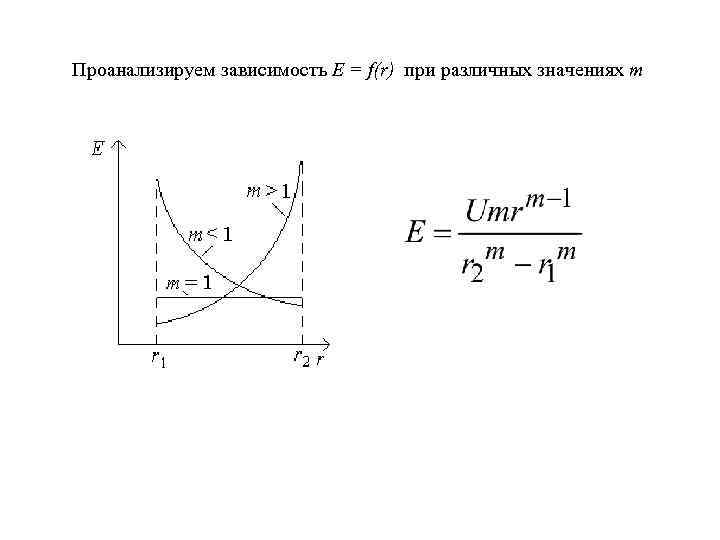
Проанализируем зависимость E = f(r) при различных значениях m

Сравнительный анализ двух кабелей Тип изоля ции Слабонагру женный Нагруженный кабель P кабель 0 k ПБИ ПЭ b m k b m 0 0 0 0 3 3 2, 2 0 0, 2, 2 7 3 1, 5

Слабонагру женный кабель P 0 Тип изоляци и Нагруженный кабель k ПБИ ПЭ b m k b m 0 0 0 0 3 3 3 1, 5 2, 2 0 0, 7 2, 2 Распределение напряженности электрического поля по толщине изоляции в кабеле постоянного тока: 1 – слабонагруженный кабель с пропитанной бумажной изоляцией; 2 – слабонагруженный кабель с полиэтиленовой изоляцией; 3 – нагруженный кабель с пропитанной бумажной изоляцией; 4 – нагруженный кабель с полиэти леновой изоляцией
ОКТ_ЭЛЕКТРИЧЕСКОЕ ПОЛЕ.ppt