Основы графической информации Лекция Аксонометрические проекции В

Основы графической информации Лекция. Аксонометрические проекции

В переводе с греческого языка слово «аксонометрия» означает измерение по осям. Особенностью аксонометрического проецирования является то, что вместе с фигурой на плоскость проецируется и пространственная система координат, связанная с этой фигурой. При этом ни одна из осей системы координат не проецируется в точку. Использование аксонометрического проецирования позволяет повысить наглядность изображения фигуры. Проекционная схема получения аксонометрической проекции простейшей фигуры – точки. Точка A и пространственная система координат Oxyz связаны координатной ломаной ОAx. A 1 A, звеньями которой являются координатные отрезки OAx = x. A , Ax. A 1 = y. A , A 1 A = z. A. Плоскость П' – аксонометрическая плоскость, s – направление проецирования. Все проецирующие прямые параллельны s. Если прямая s не перпендикулярна П', то имеем косоугольное проецирование и получим косоугольную аксонометрическую проекцию. Если прямая s перпендикулярна П', то имеем ортогональное проецирование и получим ортогональную (прямоугольную) аксонометрическую проекцию. В дальнейшем рассматривается ортогональное проецирование и ортогональные аксонометрические проекции.

Виды аксонометрических проекций При построении аксонометрических проекций необходимо учитывать, что отрезки, лежащие на осях натуральной системы координат (или им параллельные), на плоскости П´ отображаются с искажением. Отношения аксонометрических координатных отрезков к их натуральной величине характеризуют коэффициентами искажения по осям. Натуральные коэффициенты искажения обозначают так: по оси О´x´ – u, по оси О´у´ – v, по оси О´z´ – w. В зависимости от сравнительной величины коэффициентов искажения различают три вида аксонометрических проекций: изометрия (u = v = w); диметрия (u = v w, v = w u, u = w v); триметрия (u v w).

Доказано, что расположение аксонометрических осей и коэффициенты искажения по ним могут быть выбраны произвольно. При этом существует следующая зависимость между коэффициентами искажения и направлением проецирования s: u 2 + v 2 + w 2 = 2 + ctg 2 φ, (1) где φ – угол между направлением проецирования s и плоскостью П´. Для прямоугольной аксонометрии зависимость (1) имеет вид u 2 + v 2 + w 2 = 2. (2) Тогда в прямоугольной изометрии u = v = w = 0, 82, а 0, 82 в прямоугольной диметрии один коэффициент будет равен 0, 47, а два других – 0, 94. 0, 47 0, 94

Аксонометрические изображения ГОСТ 2. 317 -69 “Аксонометрические проекции” устанавливает пять видов аксонометрических проекций, рекомендованных для использования в чертежах всех отраслей промышленности и строительства: а – прямоугольная изометрия; б – прямоугольная диметрия; в – фронтальная изометрия; г – горизонтальная изометрия; д – фронтальная диметрия.

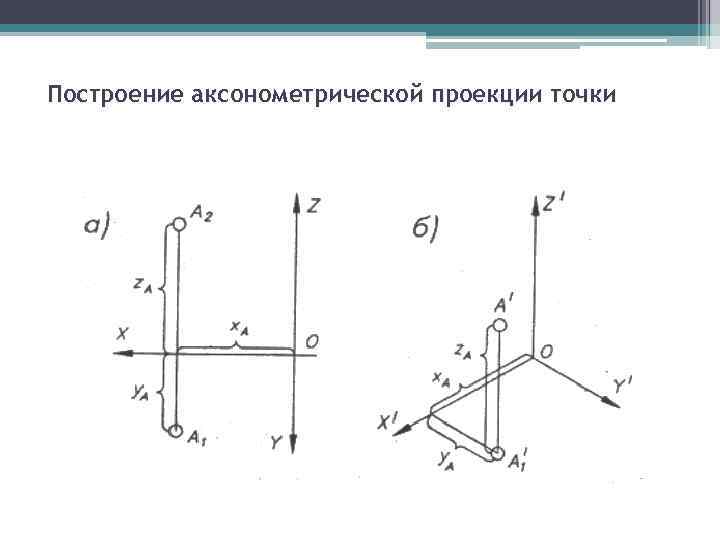Построение аксонометрической проекции точки

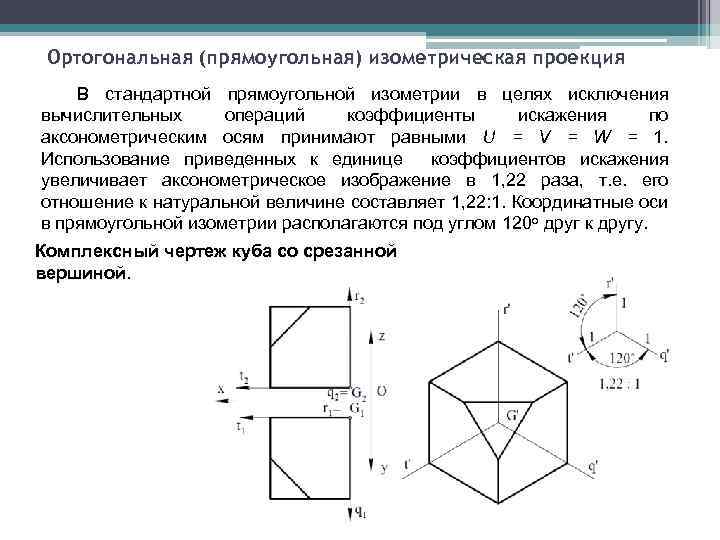Ортогональная (прямоугольная) изометрическая проекция В стандартной прямоугольной изометрии в целях исключения вычислительных операций коэффициенты искажения по аксонометрическим осям принимают равными U = V = W = 1. Использование приведенных к единице коэффициентов искажения увеличивает аксонометрическое изображение в 1, 22 раза, т. е. его отношение к натуральной величине составляет 1, 22: 1. Координатные оси в прямоугольной изометрии располагаются под углом 120 о друг к другу. Комплексный чертеж куба со срезанной вершиной.

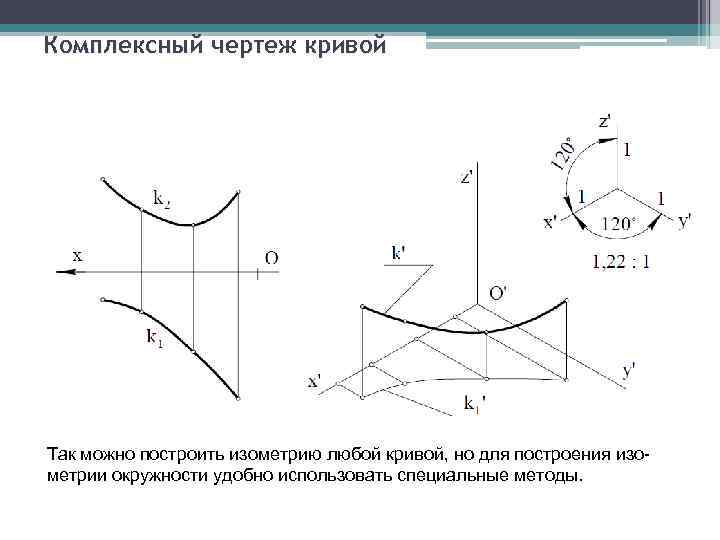Комплексный чертеж кривой Так можно построить изометрию любой кривой, но для построения изометрии окружности удобно использовать специальные методы.

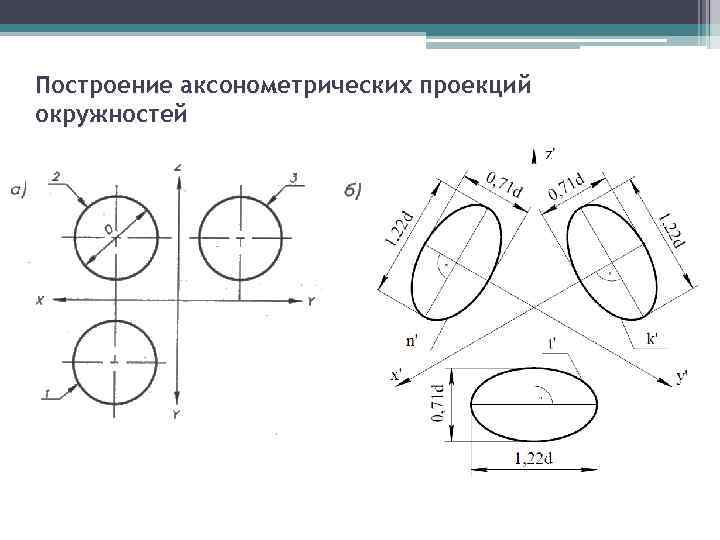Построение аксонометрических проекций окружностей

Ортогональная (прямоугольная) диметрическая проекция В стандартной прямоугольной диметрии оси располагаются, как показано на рисунке. Приведенные коэффициенты искажения U = W = 1, V = 0, 5. Масштаб изображения в этом случае равен 1, 06: 1. Диметрия куба со срезанной вершиной

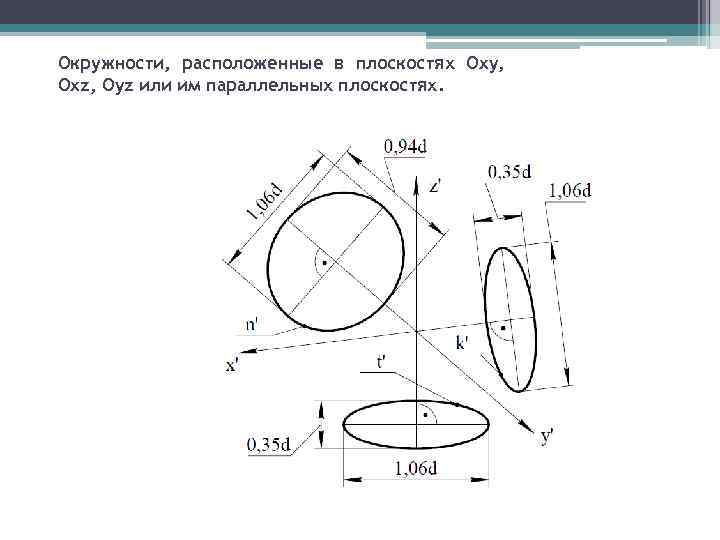Окружности, расположенные в плоскостях Oxy, Oxz, Oyz или им параллельных плоскостях.

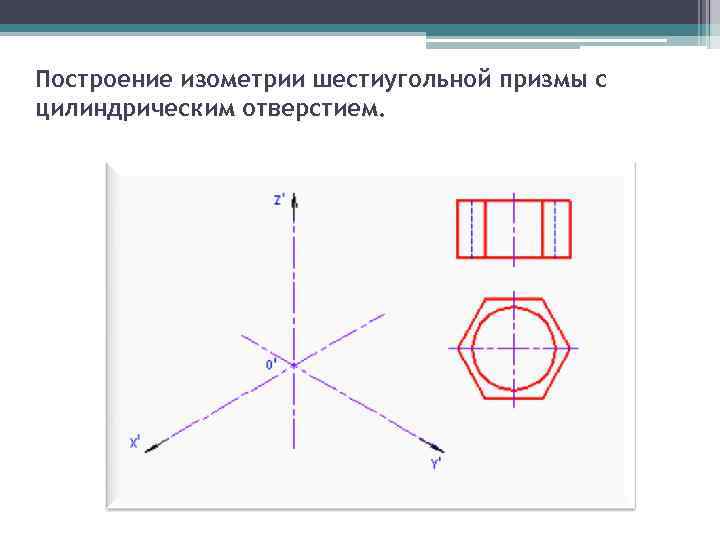Построение изометрии шестиугольной призмы с цилиндрическим отверстием.

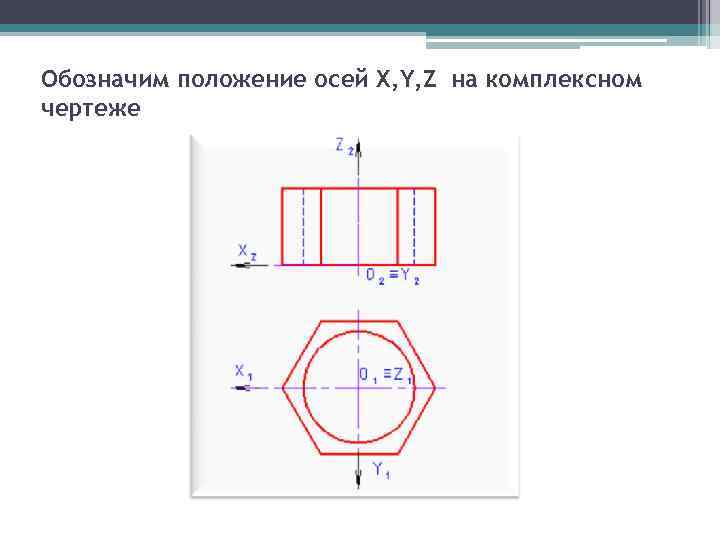Обозначим положение осей X, Y, Z на комплексном чертеже

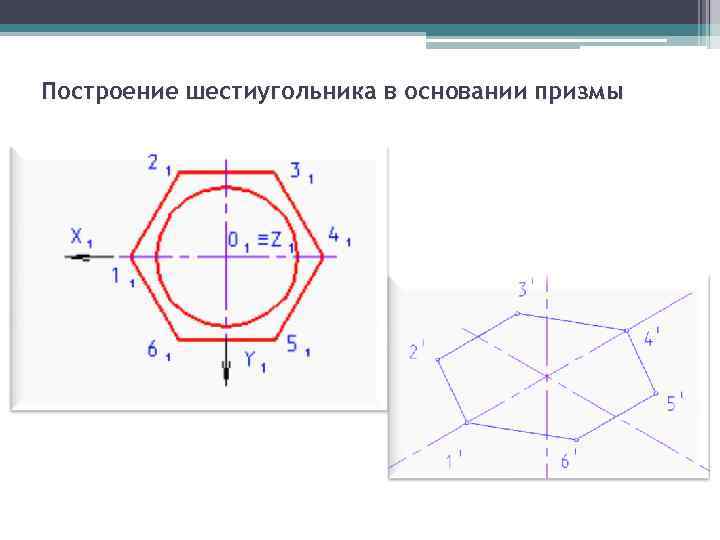Построение шестиугольника в основании призмы

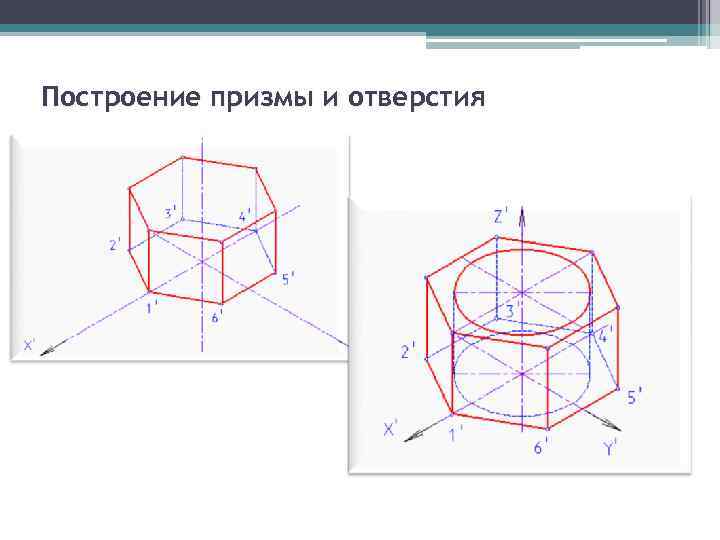Построение призмы и отверстия

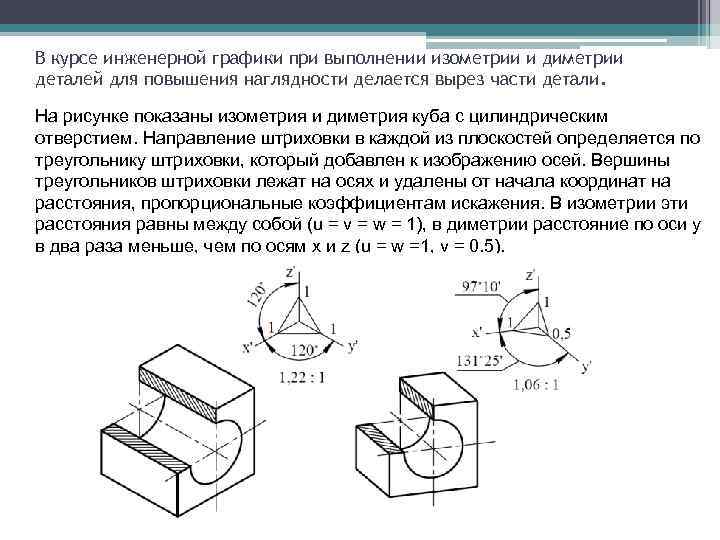В курсе инженерной графики при выполнении изометрии и диметрии деталей для повышения наглядности делается вырез части детали. На рисунке показаны изометрия и диметрия куба с цилиндрическим отверстием. Направление штриховки в каждой из плоскостей определяется по треугольнику штриховки, который добавлен к изображению осей. Вершины треугольников штриховки лежат на осях и удалены от начала координат на расстояния, пропорциональные коэффициентам искажения. В изометрии эти расстояния равны между собой (u = v = w = 1), в диметрии расстояние по оси y в два раза меньше, чем по осям x и z (u = w =1, v = 0. 5).

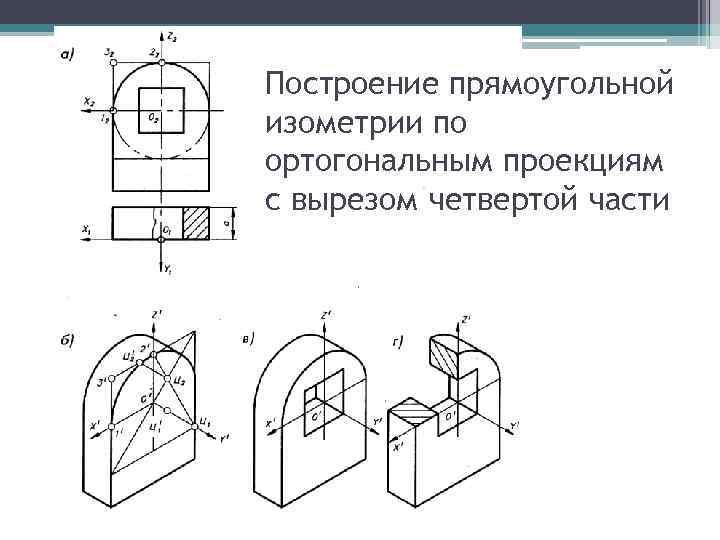Построение прямоугольной изометрии по ортогональным проекциям с вырезом четвертой части

Определение направления штриховки плоскостях проекций

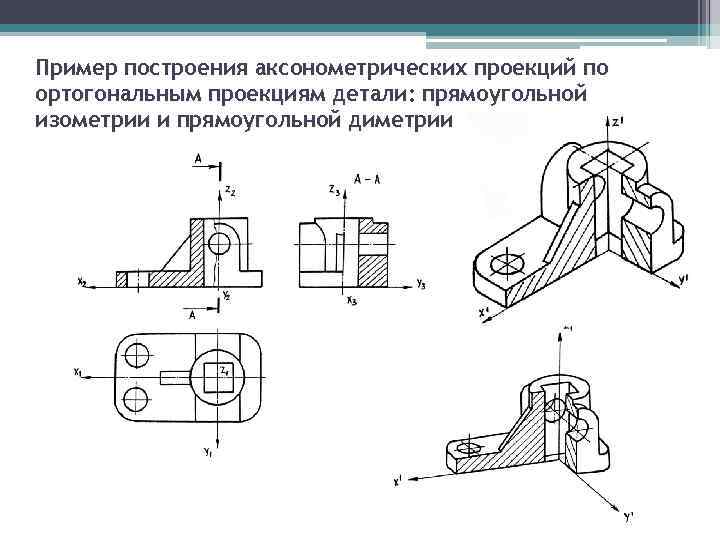Пример построения аксонометрических проекций по ортогональным проекциям детали: прямоугольной изометрии и прямоугольной диметрии