Основы функционирования систем сервиса ЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Основы функционирования систем сервиса ЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Однофазные цепи • Электрические цепи постоянного тока, в которых выполняются законы Ома и Кирхгофа, характеризуются основным параметром — сопротивлением (или проводимостью). • В таких цепях предполагается, что их параметры постоянны и не зависят от токов в элементах цепи и от напряжений на их зажимах. Элементы эти имеют линейную характеристику — прямую линию для зависимости тока от напряжения. Такие элементы называют линейными. 3

Однофазные цепи • Применение к линейным цепям законов Ома и Кирхгофа, представляющих собой линейные зависимости, приводит, как известно, к линейным алгебраическим уравнениям, решение которых не представляет собой принципиальных трудностей. • Во многих практических задачах для цепей переменного тока линейными элементами можно считать резистор, катушку индуктивности без стального сердечника и конденсатор с диэлектриком без потерь. 4

Однофазные цепи • В линейных цепях переменного тока приходится учитывать не только их активные сопротивления, в которых электрическая энергия безвозвратно преобразуется в другие виды энергии, но и так называемые реактивные сопротивления, в которых электрическая энергия «циркулирует» между этими сопротивлениями и источником переменного тока. В этих случаях исследование линейных цепей усложняется применением математических действий дифференцирования и интегрирования 5

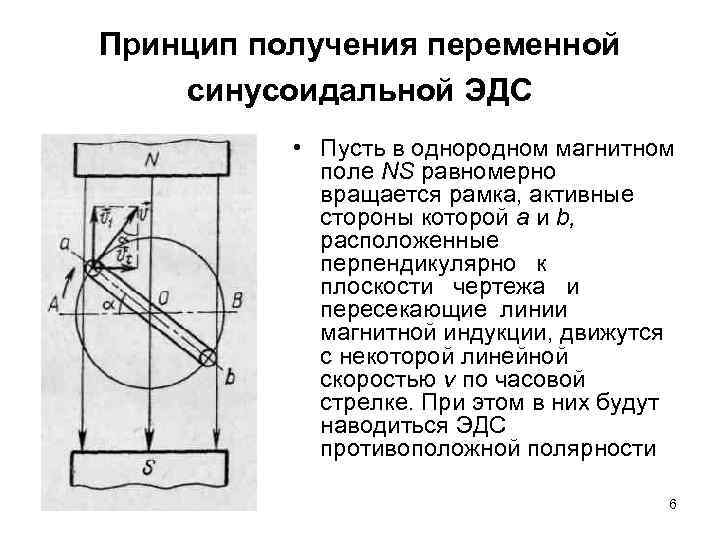Принцип получения переменной синусоидальной ЭДС • Пусть в однородном магнитном поле NS равномерно вращается рамка, активные стороны которой а и b, расположенные перпендикулярно к плоскости чертежа и пересекающие линии магнитной индукции, движутся с некоторой линейной скоростью ν по часовой стрелке. При этом в них будут наводиться ЭДС противоположной полярности 6

Принцип получения переменной синусоидальной ЭДС е =Blvt = Blvsinα 7

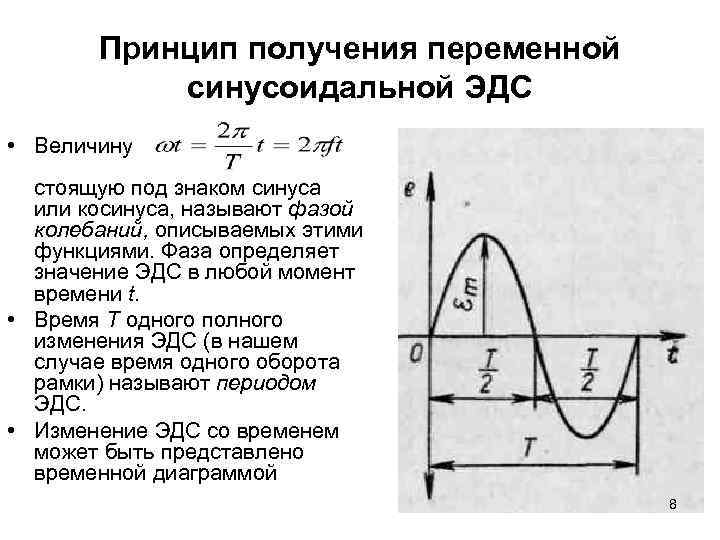Принцип получения переменной синусоидальной ЭДС • Величину стоящую под знаком синуса или косинуса, называют фазой колебаний, описываемых этими функциями. Фаза определяет значение ЭДС в любой момент времени t. • Время Т одного полного изменения ЭДС (в нашем случае время одного оборота рамки) называют периодом ЭДС. • Изменение ЭДС со временем может быть представлено временной диаграммой 8

Действующие значения тока и напряжения • Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. 9

Среднее значение переменного тока 10

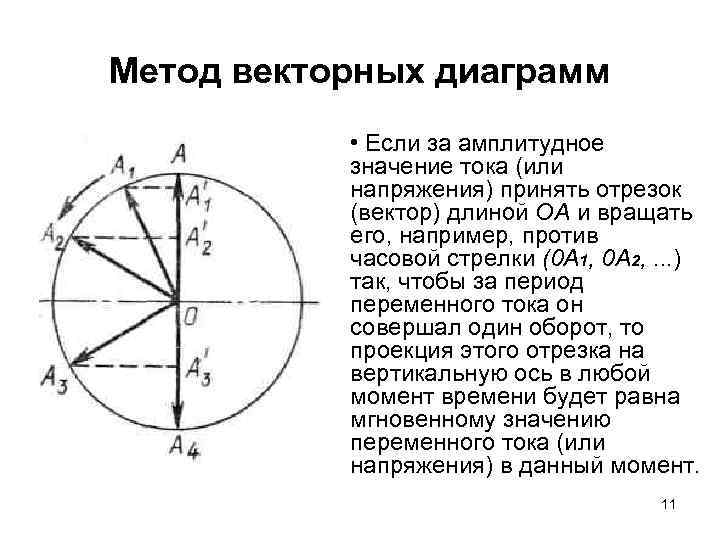Метод векторных диаграмм • Если за амплитудное значение тока (или напряжения) принять отрезок (вектор) длиной ОА и вращать его, например, против часовой стрелки (0 A 1, 0 А 2, . . . ) так, чтобы за период переменного тока он совершал один оборот, то проекция этого отрезка на вертикальную ось в любой момент времени будет равна мгновенному значению переменного тока (или напряжения) в данный момент. 11

Метод векторных диаграмм • Если изобразить две периодические величины (например ток и напряжение) в выбранных масштабах (изменения этих величин происходят с одинаковой частотой, но отличаются по фазе на некоторый угол), то при вращении их векторов угол сдвига фаз (угол между векторами) остается постоянным в течение всего периода (оборота). 12

Метод векторных диаграмм Этот способ и положен в основу метода векторных диаграмм: • а) длину вектора выбирают равной (в масштабе) амплитуде изображаемой периодической величины, а направление произвольное; • б) при построении нескольких векторов на одном и том же чертеже один из них выбирают основным и направляют произвольно, а остальные — в соответствии со сдвигом по фазе относительно основного; • в) поворот вектора против часовой стрелки соответствует опережению по фазе, по часовой — отставанию по фазе. 13

Метод векторных диаграмм • На одной и той же векторной диаграмме могут быть изображены периодические величины только равных частот. Одна и та же векторная диаграмма справедлива как для амплитудных, так и для действующих значений периодических величин (разные лишь масштабы). • Метод векторных диаграмм очень нагляден. По правилам векторного сложения легко осуществляют сложение и вычитание векторов, а вместе с этим — сложение и вычитание самих переменных величин. 14

Сопротивления в цепях переменного тока • Как известно, металлический проводник оказывает электрическому току вполне определенное сопротивление, обусловленное материалом, из которого он изготовлен, и размерами этого проводника. Но один и тот же проводник поразному ведет себя в цепях постоянного и переменного токов, оказывая им разные сопротивления. Так, в результате поверхностного эффекта проводник оказывает большее сопротивление переменному току, нежели постоянному. Правда, при промышленной частоте 50 Гц разница между этими сопротивлениями весьма незначительна и на практике их считают равными. Однако сопротивления, оказываемые переменному току катушкой индуктивности (индуктивностью) и конденсатором (емкостью) коренным образом отличаются от сопротивления, которым обладает резистор (например, электронагревательный прибор). 15

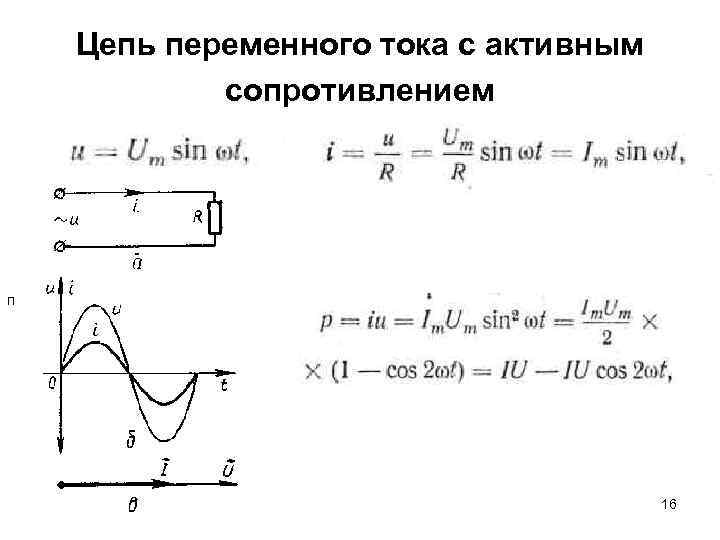Цепь переменного тока с активным сопротивлением П 16

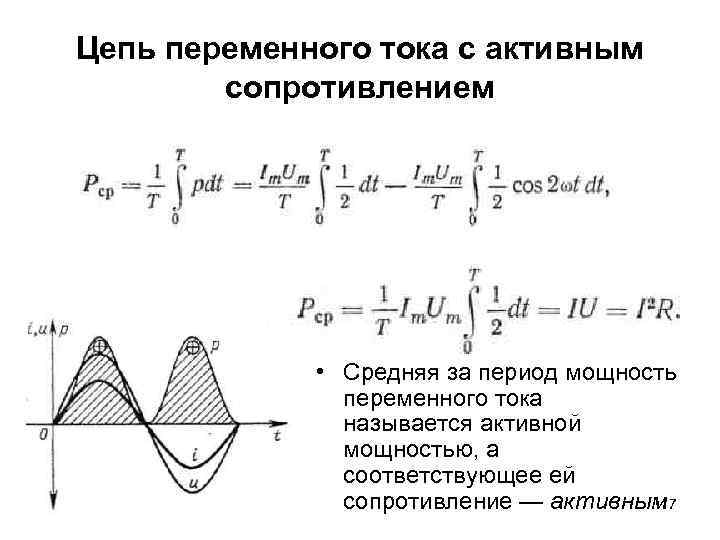Цепь переменного тока с активным сопротивлением • Средняя за период мощность переменного тока называется активной мощностью, а соответствующее ей 17 сопротивление — активным.

Цепь переменного тока с индуктивностью 18

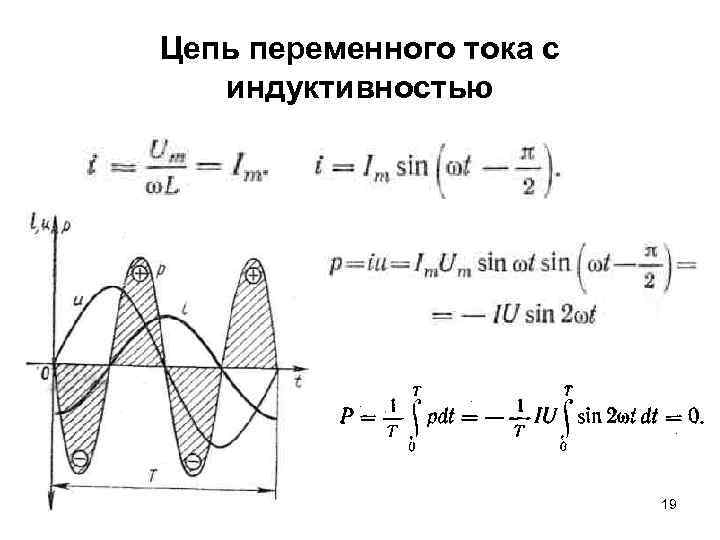Цепь переменного тока с индуктивностью 19

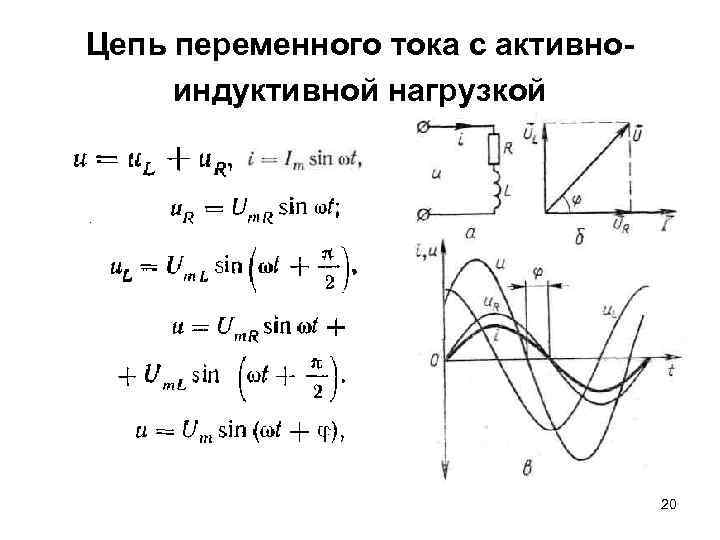Цепь переменного тока с активноиндуктивной нагрузкой 20

Цепь переменного тока с активноиндуктивной нагрузкой 21

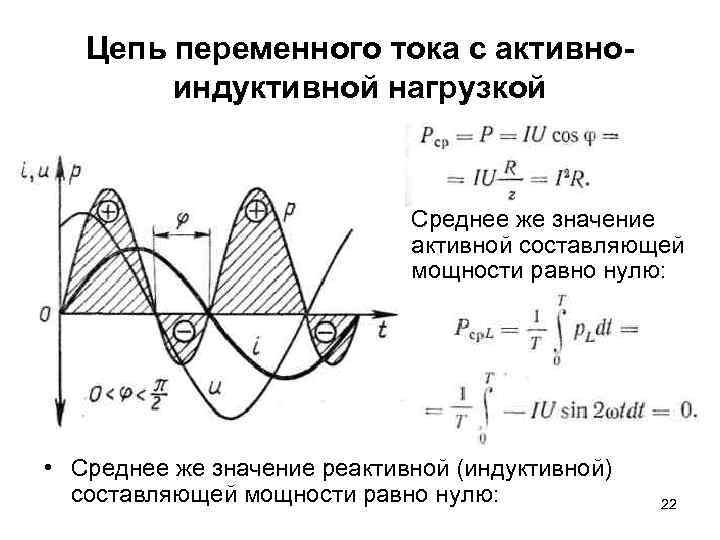Цепь переменного тока с активноиндуктивной нагрузкой • Среднее же значение активной составляющей мощности равно нулю: • Среднее же значение реактивной (индуктивной) составляющей мощности равно нулю: 22

Цепь переменного тока с активноиндуктивной нагрузкой • В цепи переменного тока с активной R и индуктивной L нагрузкой угол сдвига фаз между током и напряжением зависит от соотношения значений Rи. L • Угол сдвига фаз изменяется в пределах 0 < φ < π/2. • Среднее значение активной составляющей мощности Pcp=I 2 R • Среднее значение реактивной (индуктивной) составляющей мощности PLcp=0 23

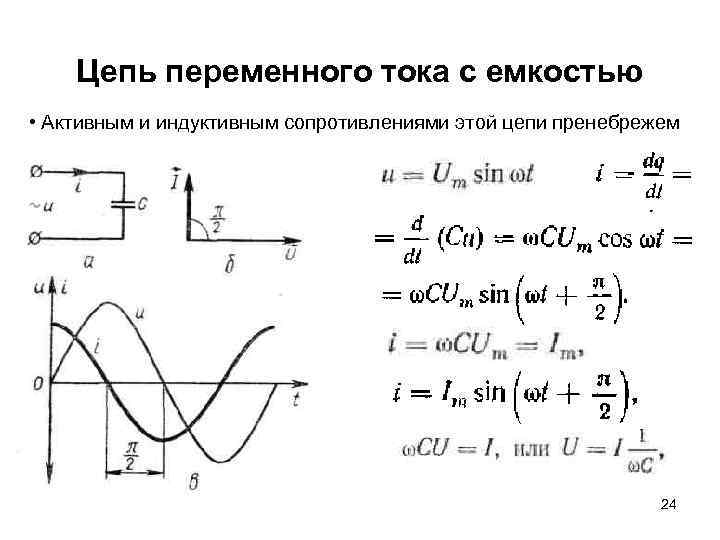Цепь переменного тока с емкостью • Активным и индуктивным сопротивлениями этой цепи пренебрежем 24

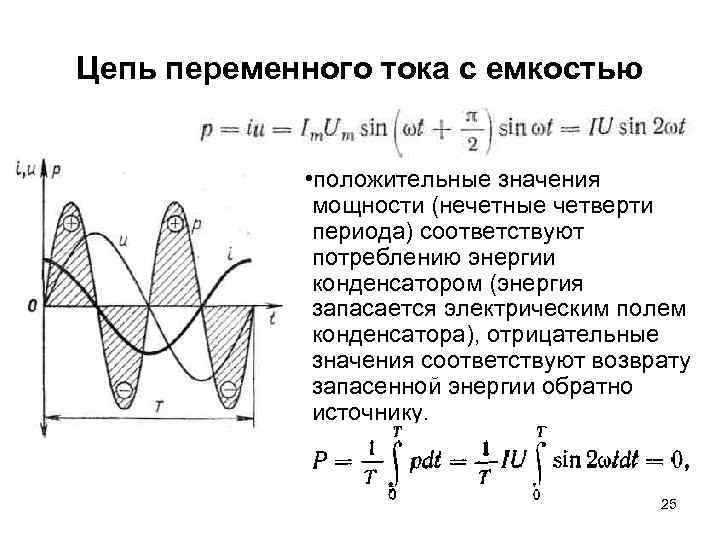Цепь переменного тока с емкостью • положительные значения мощности (нечетные четверти периода) соответствуют потреблению энергии конденсатором (энергия запасается электрическим полем конденсатора), отрицательные значения соответствуют возврату запасенной энергии обратно источнику. 25

Цепь переменного тока с активноемкостной нагрузкой 26

Цепь переменного тока с активноемкостной нагрузкой • При синусоидальном токе напряжение на конденсаторе также синусоидально. При • Следовательно, приложенное напряжение и является также синусоидальным, поэтому допущение о синусоидальной форме тока правильное 27

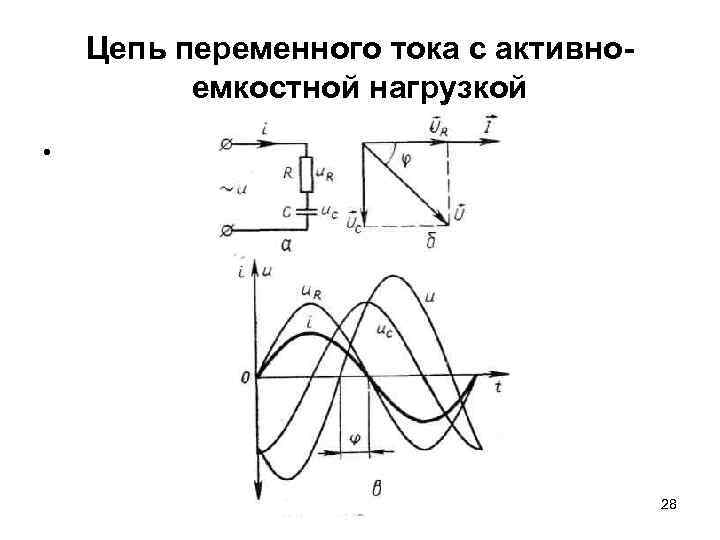Цепь переменного тока с активноемкостной нагрузкой • Для рассматриваемой цепи приложенное напряжение 28

Цепь переменного тока с активноемкостной нагрузкой • Для выяснения закона изменения мощности в цепи с R и С представим ток и напряжение в следующем виде: • тогда мгновенное значение мощности равно • при φ=0 цепь становится чисто активной • при φ=π/2 цепь становится чисто емкостной 29

Цепь переменного тока с активноемкостной нагрузкой 30

Последовательное соединение R, L и С. Коэффициент мощности • Рассмотрим цепь переменного тока, состоящую из последовательно соединенных R, L и С. Условие электрического равновесия для такой цепи следующее 31

Последовательное соединение R, L и С. Коэффициент мощности 32

Последовательное соединение R, L и С. Коэффициент мощности • Закон Ома для цепи переменного тока, содержащей R, L и С, имеет вид 33

Последовательное соединение R, L и С. Коэффициент мощности • Реактивная мощность Q всегда порождает наличие обменной энергии. Её измеряют в вольт-амперах реактивных (ВАр) и киловольт-амперах реактивных (к. ВАр). • Полную мощность S, содержащую в себе активную и реактивную мощности, иначе называют кажущейся, т. е. такой, которую может дать источник (генератор, трансформатор) • Единицами измерения полной мощности являются вольт ампер (ВА) и киловольт ампер (к. ВА). Эта мощность и указывается в паспортах генератора и трансформатора переменного тока 34

Последовательное соединение R, L и С. Коэффициент мощности • Активная мощность Р соответствует электрической энергии, используемой для совершения механической работы, для получения теплоты и т. д. Она измеряется в ваттах (Вт) и киловаттах (к. Вт): • Множитель cos φ называют коэффициентом мощности. • Для более рационального использования мощности станции надо стремиться сделать нагрузку такой, чтобы cos φ = 1. Однако на практике в масштабе промышленного предприятия добиться этого весьма трудно, хотя часто значение cos φ доводят до 0, 9— 0, 95. • Низкие значения cos φ порождают значительные дополнительные потери на нагревание проводов обмоток генератора и линий электропередач. 35

Последовательное соединение R, L и С. Коэффициент мощности • Пусть одинаковые активные мощности передаются к двум равным нагрузкам с cosφ = 1 и с cosφ < 1 • Так как реактивная мощность растёт с уменьшением cosφ. Она создает в проводах дополнительный реактивный ток и потери на теплоту пропорциональные квадрату тока. • Повышение cosφ является задачей государственной важности. • Так, повышение cosφ в энергосистемах России всего лишь на 0, 01 может дать экономию более 1 млрд рублей. 36

Резонанс напряжений • В последовательной цепи с R, L и С приложенное напряжение U равно сумме падений напряжений на активном сопротивлении, индуктивности и емкости. Из векторной диаграммы находим • Обозначив полное сопротивление цепи через z: • Закон Ома для данной цепи можно записать: 37

Резонанс напряжений • В рассматриваемой цепи при x. L > xc нагрузка является активно индуктивной, а при x. L < хс — активно емкостной. • Важным является случай, когда x. L = xc. Тогда ток в цепи равен • т. е. цепь в данном случае имеет наименьшее возможное сопротивление, как будто в нее включено только активное сопротивление R. При этом напряжения на индуктивности и емкости UL и UC, сдвинутые по фазе на π, полностью компенсируют друга (рис. ). Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, и ток совпадает по фазе с напряжением. Этот случай получил название резонанса напряжений. 38

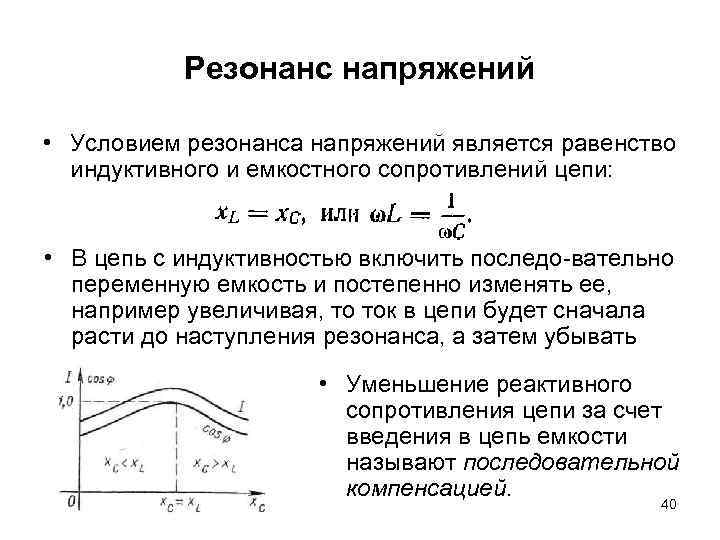Резонанс напряжений • Условием резонанса напряжений является равенство индуктивного и емкостного сопротивлений цепи: • В цепь с индуктивностью включить последо вательно переменную емкость и постепенно изменять ее, например увеличивая, то ток в цепи будет сначала расти до наступления резонанса, а затем убывать • Уменьшение реактивного сопротивления цепи за счет введения в цепь емкости называют последовательной компенсацией. 40

Резонанс напряжений • При х. С < x. L получается недокомпенсация. • При х. С > x. L — перекомпенсация. • При х. С = x. L —полная компенсация (ток становится максимальным, а cosφ = 1). • Такой способ компенсации иногда применяют на практике для повышения cosφ в сетях. • Отношение приложенного напряжения к напряжению индуктивного (или емкостного) участка при x. L > R напряжение на реактивном участке UL (и равное ему UC) окажется больше приложенного в раз 41

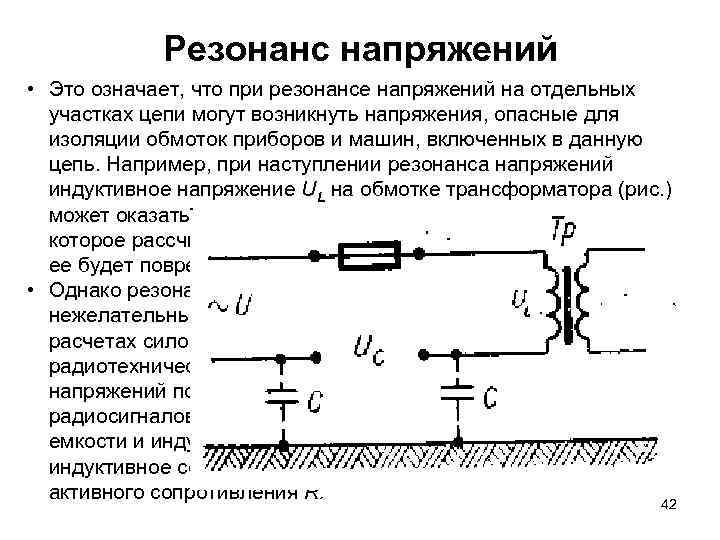Резонанс напряжений • Это означает, что при резонансе напряжений на отдельных участках цепи могут возникнуть напряжения, опасные для изоляции обмоток приборов и машин, включенных в данную цепь. Например, при наступлении резонанса напряжений индуктивное напряжение UL на обмотке трансформатора (рис. ) может оказаться значительно больше того напряжения, на которое рассчитана сама обмотка, в результате чего изоляция ее будет повреждена. • Однако резонанс напряжений может быть не только нежелательным явлением, которое приходится учитывать при расчетах силовых цепей, но и полезным. В частности, в радиотехнических колебательных контурах благодаря резонансу напряжений получают значительное усиление слабых радиосигналов за счет образования больших напряжений на емкости и индуктивности. Для этого специально делают индуктивное сопротивление контура x. L во много раз больше его активного сопротивления R. 42

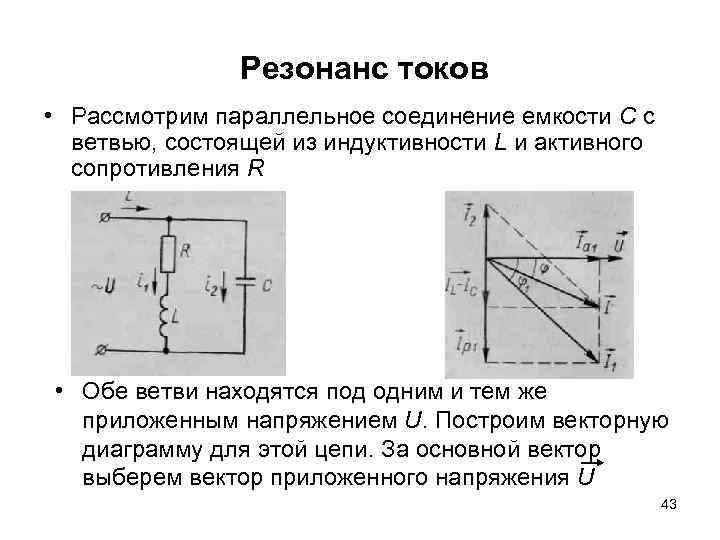Резонанс токов • Рассмотрим параллельное соединение емкости С с ветвью, состоящей из индуктивности L и активного сопротивления R • Обе ветви находятся под одним и тем же приложенным напряжением U. Построим векторную диаграмму для этой цепи. За основной вектор выберем вектор приложенного напряжения U 43

Резонанс токов отложим этот вектор по отношению к вектору U под углом φ1 определяемым по формуле длина и положение вектора общего тока зависят от соотношения реактивных токов IL и IС. В частности, при IL > IС общий ток может отставать по фазе от приложенного напряжения, при IL < IС— опережать и, наконец, при IL = IС— совпадать по фазе с приложенным напряжением. 44

Резонанс токов • Последний случай соотношения реактивных токов ветвей (IL = IС) получил название резонанса токов. При резонансе токов общий ток равен активной составляющей тока в катушке, т. е. процессы в цепи таковы, будто в ней содержится только активное сопротивление (в этом случае φ = 0 и cosφ = 1). • Таким образом, подключение емкости параллельно катушке индуктивности уменьшает угол сдвига фаз между током и напряжением как и при последовательном их соединении. Но параллельное подключение имеет и свою особенность: общий ток в цепи при этом уменьшается и становится чисто активным, хотя в самих ветвях реактивные токи не равны нулю; реактивные же токи имеют противоположные фазы. 45

Резонанс токов • При увеличении тока в катушке потребляемая энергия запасается в магнитном поле, а в конденсаторе, наоборот, при увеличении приложенного напряжения энергия запасается в электрическом поле. Катушка и конденсатор обмениваются между собой энергией, освобождая тем самым линию и генератор от реактивного тока. Эту особенность параллельной цепи используют как параллельную компенсацию (реактивные токи взаимно компенсируются) для повышения cosφ. 46

Способы повышения коэффициента мощности • Одной из причин низкого значения cosφ является неполная загрузка асинхронных электродвигателей, так как активная мощность определяется активной нагрузкой, тогда как реактивная зависит от общей мощности двигателя, его типа и загрузки. Следовательно, неправильный выбор типа двигателя и его мощности (с запасом) приводит к понижению значения cosφ • Важнейшим условием рационального использования электроэнергии (т. е. повышения cosφ) является полная загрузка электродвигателя и недопущение его длительной работы на холостом ходу, правильный выбор типа двигателя и его мощности. Такой способ повышения cosφ называют естественным. 47

Способы повышения коэффициента мощности • Одним из наиболее распространенных способов искусственного повышения cosφ является компенсация сдвига фаз между напряжением и общим током в цепи потребителя (или группы потребителей). Например, параллельно двигателю Д подключают конденсатор. Компенсация сводится к тому, что за счет емкостного тока Ic конденсатора уменьшается сдвиг по фазе между током и напряжением в цепи двигателя. Путем подбора емкости конденсатора С можно довести значение сдвига по фазе до нуля. 48

Способы повышения коэффициента мощности • Физическая сущность явления компенсации состоит в том, что. двигатель, например, в четные четверти периода запасает энергию в магнитном поле, а в нечетные — отдает ее, а конденсатор, наоборот, в нечетные четверти периода запасает энергию в электрическом поле, а в четные— отдает ее. Причем энергия, накапливаемая в магнитном поле двигателя и в электрическом поле конденсатора, является «обменной» (неиспользуемой) энергией. Таким образом, обменная энергия будет частично или полностью «циркулировать» между магнитным полем двигателя и электрическим полем конденсатора. При установившемся режиме работы источник тока и линия электропередачи будут частично или полностью разгружены от «обменной» энергии. 49

Способы повышения коэффициента мощности • Однако искусственные методы не позволяют в данной цепи избавиться от «обменной» энергии, они могут лишь локализовать ее, освобождая при этом сети и их станции. Практическое применение конденсаторов для компенсации несколько ограничено из за их высокой стоимости. Поэтому на практике получили широкое распространение так называемые синхронные компенсаторы — синхронные двигатели облегченной конструкции, работающие на холостом ходу и создающие емкостный ток. 50

Проводимость и расчет электрических цепей • В курсе общей физики для расчета электрических цепей используют, в основном, законы Ома и Кирхгофа, в которые входят напряжения, токи и сопротивления. Однако для расчета сложных электрических цепей, и в особенности цепей переменного тока, целесообразно вместо сопротивления использовать проводимость. • Проводимость в цепи постоянного тока g— величина, обратная сопротивлению R: 51

Проводимость и расчет электрических цепей • Единицей измерения проводимости в СИ является сименс (в честь немецкого электротехника XIX в. Э. В. Сименса). • 1 Сим — это проводимость проводника сопротивлением 1 Ом. • В цепях переменного тока, как известно, существует три типа сопротивлений: активное R, реактивное х и полное z. По аналогии с этим введено и три типа проводимостей: активная g, реактивная b и полная у. Однако только полная проводимость у является величиной, обратной полному сопротивлению z: 52

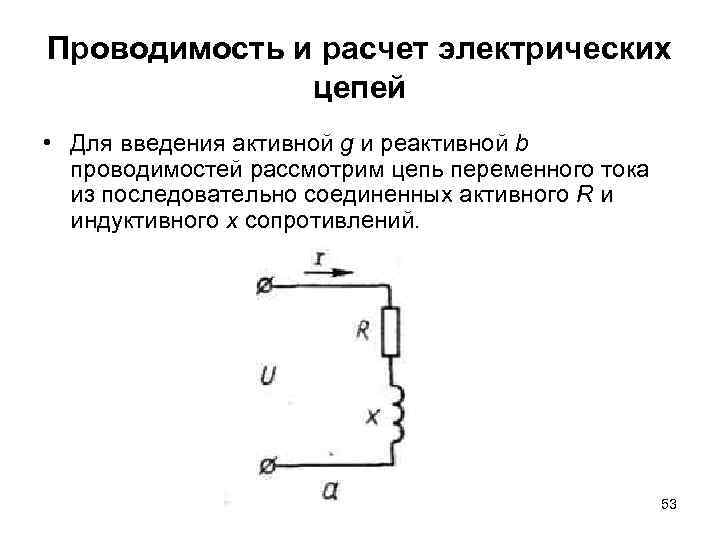Проводимость и расчет электрических цепей • Для введения активной g и реактивной b проводимостей рассмотрим цепь переменного тока из последовательно соединенных активного R и индуктивного х сопротивлений. 53

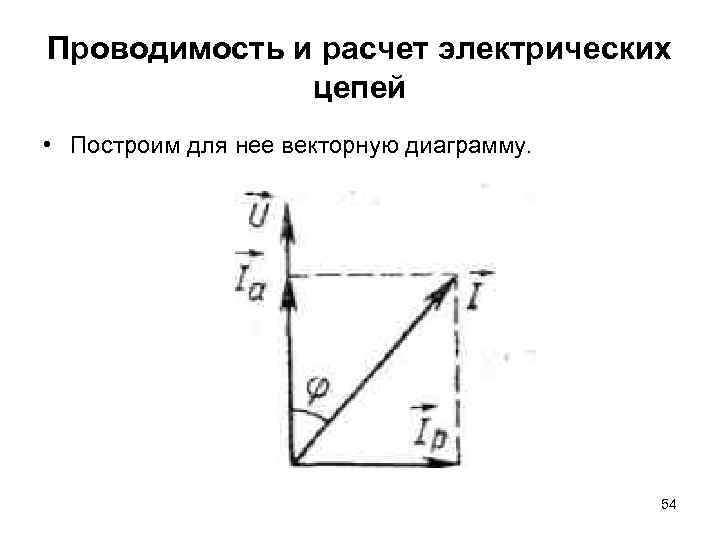Проводимость и расчет электрических цепей • Построим для нее векторную диаграмму. 54

Проводимость и расчет электрических цепей • Ток в цепи I разложим на активную Iа и реактивную Iр составляющие и от полученного треугольника токов перейдем к треугольнику сопротивлений. Из последнего имеем: 55

Проводимость и расчет электрических цепей • векторной диаграммы с учетом формулы имеем: — активная проводимость — реактивная проводимость. 56

Проводимость и расчет электрических цепей • Установим взаимосвязь между проводимостями. Для рассматриваемой цепи имеем: • Подставив значения Iа и Iр получим: — полная проводимость цепи. 57

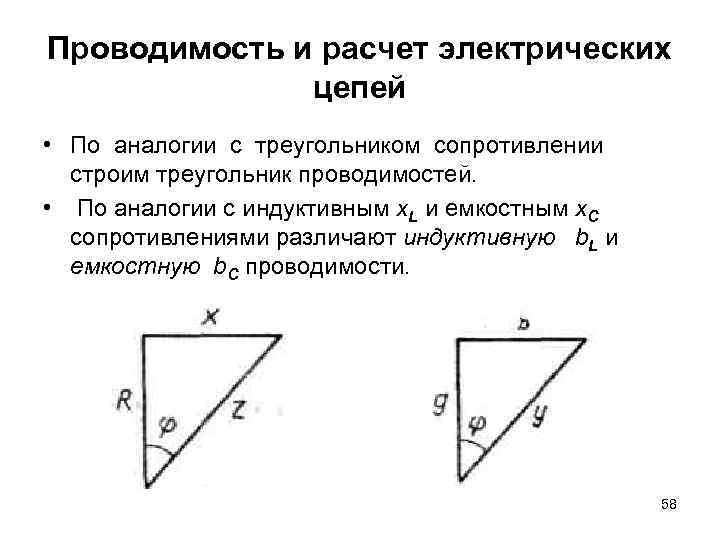Проводимость и расчет электрических цепей • По аналогии с треугольником сопротивлении строим треугольник проводимостей. • По аналогии с индуктивным x. L и емкостным х. С сопротивлениями различают индуктивную b. L и емкостную b. С проводимости. 58

Проводимость и расчет электрических цепей • В случае разветвленной цепи (рис. а) схему легко преобразовать в так называемую эквивалентную схему (рис. б), в которой две ветви заменены одной с соответствующими эквивалентными активным RЭ, и реактивным х. Э сопротивлениями. 59

Проводимость и расчет электрических цепей • Расчет последних сопротивлений, как и других параметров схемы, проще с использованием проводимостей. Установим основные закономерности для проводимостей в разветвленной цепи. • Выразим общий ток через его составляющие или эквивалентные проводимости: • В свою очередь, активная составляющая общего тока равна сумме активных составляющих токов ветвей: 60

Проводимость и расчет электрических цепей • Так как реактивные составляющие ветвей рассматриваемой цепи находятся в противофазе, то для реактивной составляющей общего тока имеем: • т. е. эквивалентная реактивная проводимость разветвления равна алгебраической сумме реактивных проводимостей параллельных ветвей, при этом b. L берется со знаком «плюс» , а b. С — со знаком «минус» . 61

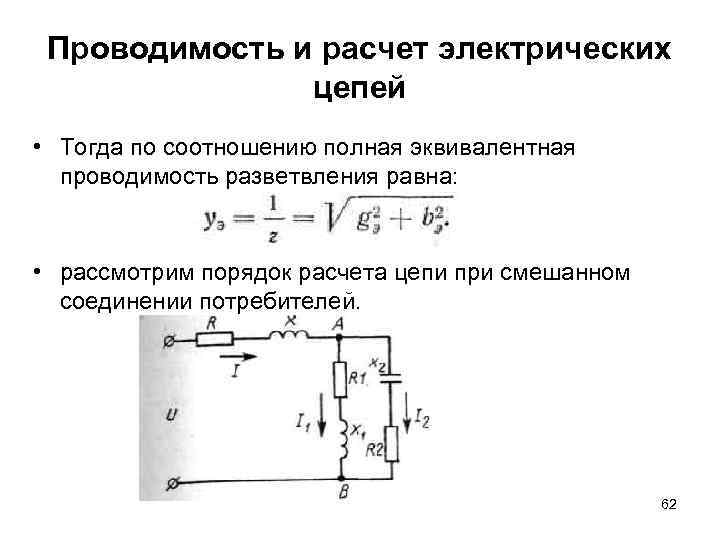Проводимость и расчет электрических цепей • Тогда по соотношению полная эквивалентная проводимость разветвления равна: • рассмотрим порядок расчета цепи при смешанном соединении потребителей. 62

Проводимость и расчет электрических цепей • Сначала параллельные ветви заменяем эквивалентной схемой из RЭ и х. Э, для чего по найденным активным g 1 и g 2, реактивным b 1 и b 2 и полным у1 и у2 проводимостям находим эквивалентные проводимости g. Э, b. Э и у. Э, а затем и эквивалентные сопротивления RЭ и х. Э 63

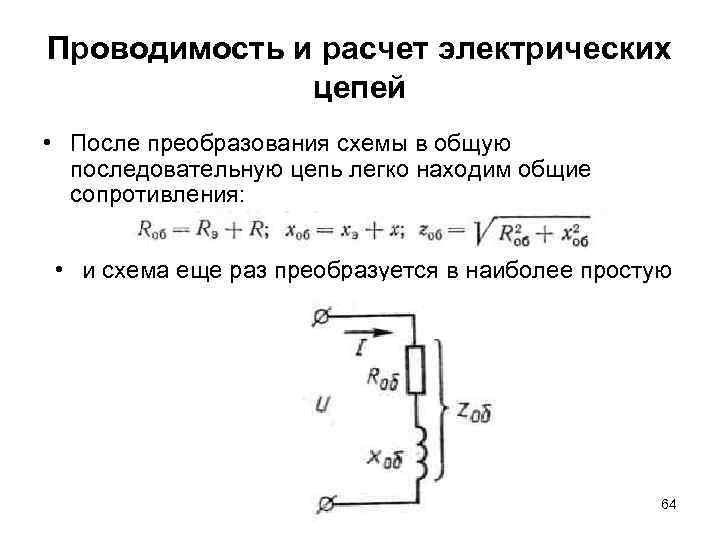Проводимость и расчет электрических цепей • После преобразования схемы в общую последовательную цепь легко находим общие сопротивления: • и схема еще раз преобразуется в наиболее простую 64

Проводимость и расчет электрических цепей • По этой схеме находят основные параметры цепи: 65

Символический метод • Для расчета цепей переменного тока, а также для анализа процессов в электрических машинах широкое применение получил так называемый символический метод, основанный на использовании комплексных чисел. Поэтому символический метод часто называют еще комплексным методом. • Комплексное число Á может быть записано в трех формах: алгебраической, тригонометрической и показательной: — модуль комплексного числа — аргумент, показывающий ориентировку вектора на числовой плоскости, 66

Символический метод • Если аргумент α изменяется со временем, например α=ωt, то точка на числовой плоскости, соответствующая комплексному числу Á = Аејωt, описывает окружность радиуса А с центром в начале координат. Поэтому комплексное число Á = Аејωt может быть представлено вектором А, вращающимся против часовой стрелки с угловой скоростью ω. Эта особенность комплексных чисел и дает возможность применять их к гармонически изменяющимся величинам. • Пусть в некоторой цепи напряжение и ток изменяются по закону синуса с разностью фаз φ : 67

Символический метод • В активно индуктивной цепи (рис. а и б), где за основной вектор выбран вектор тока I, комплекс тока ĺ будет равен ĺ=I, вектор UR = RI совпадает с вектором тока I, поэтому комплекс падения напряжения на активном сопротивлении равен Ú=Rĺ • Вектор UL (длина которого UL= =x. L = ωLI) опережает вектор тока I на π/2, поэтому комплекс этого вектора ÚL равен 68

Символический метод • По второму закону Кирхгофа приложенное напряжение U равно или в комплексной форме — комплекс полного сопротивления (не вектор!) для активно индуктивной цепи; — сдвиг фаз. • Тогда закон Ома для цепи переменного тока в комплексной форме имеет вид 69

Символический метод • для активно индуктивной цепи можно записать • комплекс полного сопротивления z может быть выражен и в показательной форме: 70

Символический метод • В активно емкостной цепи (рис. а и б), 71

Символический метод • Для получения мощности в комплексной форме принято брать произведение комплекса напряжения Ú на сопряженный комплекс тока ĺ. • Здесь вещественная часть IUcos φ представляет собой активную мощность, а мнимая IUsin φ (без множителя ј) — реактивную. Модуль комплекса мощности дает полную (кажущуюся) мощность 72

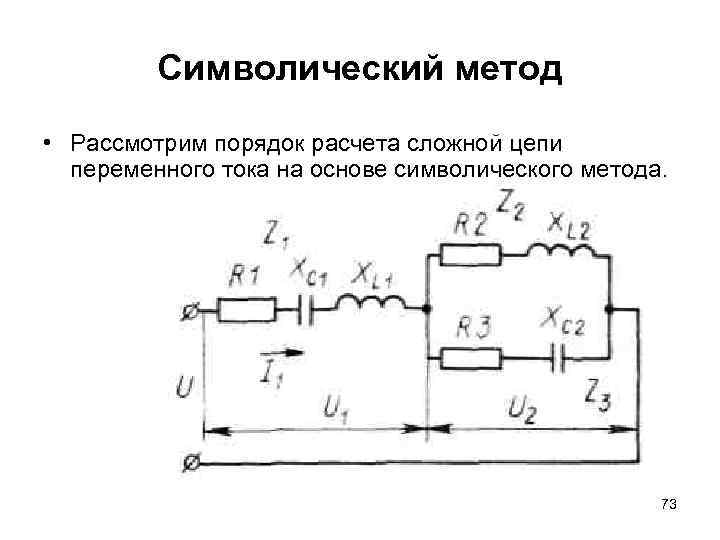Символический метод • Рассмотрим порядок расчета сложной цепи переменного тока на основе символического метода. 73

Символический метод • Пусть известно приложенное напряжение и все сопротивления, включенные в цепь. Необходимо найти токи. • Сначала записываем комплексы полных сопротивлений участков цепи: • Затем находим комплекс полного сопротивления z всей цепи: 74

Символический метод • комплекс общего тока • Так как то • По комплексам токов можно найти их модули (действующие значения). 75

Трехфазные цепи • Занимаясь усовершенствованием методов применения переменного тока, югославский изобретатель Н. Тесла изобрел двухфазную систему переменного тока, в которой одновременно действовали два напряжения равной амплитуды и частоты, но сдвинутые по фазе на 90° друг относительно друга. Двухфазная система переменного тока имеет ряд преимуществ по сравнению с однофазной. 76

Трехфазные цепи • Значительно более совершенной оказалась трехфазная система переменного тока, впервые теоретически обоснованная и практически осуществленная выдающимся русским электротехником конца XIX и начала XX в. М. О. Доливо Добровольским. В трехфазной системе одновременно действуют три напряжения равной частоты и амплитуды, но сдвинутые по фазе друг относительно друга на 120°. • Это изобретение относится к 1889 г. , а в 1891 г. на Всемирной технической выставке во Франкфурте на Майне М. О. Доливо Добровольским была осуществлена передача электроэнергии по трехфазной системе. 77

Трехфазные цепи • Гидротурбина, построенная на водопаде Неккар, расположенном в 175 км от выставки, приводила в действие трехфазный генератор, напряжение от которого повышалось трехфазным трансформатором до 8500 В. Во Франкфурте это напряжение понижалось другим трансформатором до 65 В. Током низкого напряжения питались 1000 ламп накаливания и трехфазный асинхронный двигатель, приводящий в действие водяной насос. Генератор, трансформатор и асинхронный двигатель были разработаны М. О. Доливо Добровольским для трехфазной системы. В этой передаче М. О. Доливо Добровольский при передаваемой мощности 220 к. ВА получил очень высокий по тому времени КПД, равный 77, 4%. 78

Трехфазные цепи • Следует заметить, что в 1882 г. французский электротехник Депре в опыте передачи энергии постоянным током на расстояние 57 км при напряжении 2000 В получил КПД всего лишь 22%. • Понятно, что электропередача М. О. Доливо Добровольского во Франкфурте привлекла внимание электротехников своими достоинствами и трехфазная система быстро заняла ведущее положение в мировой электротехнике. 79

Трехфазные цепи • Основные достоинства трехфазной системы: • простота конструкции и эксплуатации трехфазных двигателей, • большая экономия в массе проводов при передаче электроэнергии на большие расстояния, достигающая 20— 30% по сравнению с однофазной системой, • возможность получения различных напряжений (линейные и фазные) в одной и той же трехфазной системе. 80

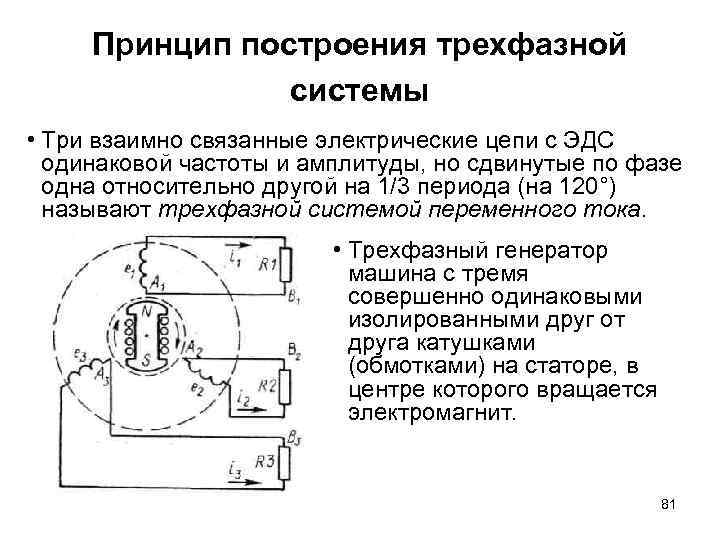Принцип построения трехфазной системы • Три взаимно связанные электрические цепи с ЭДС одинаковой частоты и амплитуды, но сдвинутые по фазе одна относительно другой на 1/3 периода (на 120°) называют трехфазной системой переменного тока. • Трехфазный генератор машина с тремя совершенно одинаковыми изолированными друг от друга катушками (обмотками) на статоре, в центре которого вращается электромагнит. 81

Принцип построения трехфазной системы • Пусть при этом форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по косинусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут индуцироваться синусоидальные ЭДС равной амплитуды и частоты, но отличные друг от друга по фазе на 120° • Эти три ЭДС, можно изобразить на временной и на векторной диаграммах 82

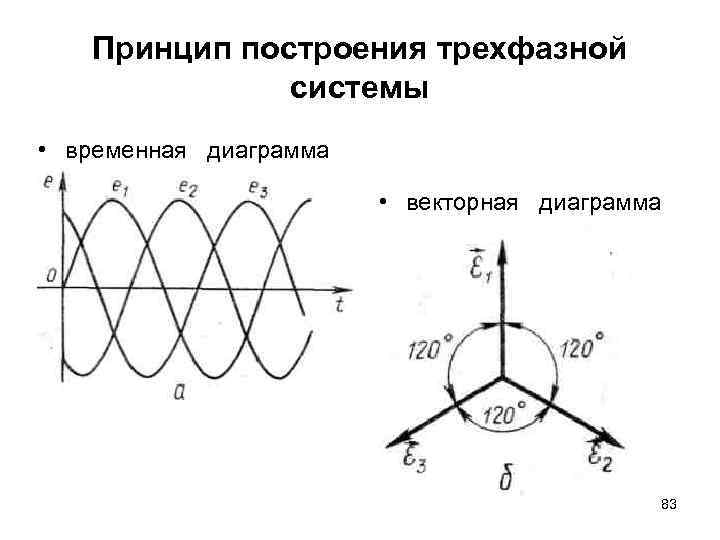Принцип построения трехфазной системы • временная диаграмма • векторная диаграмма 83

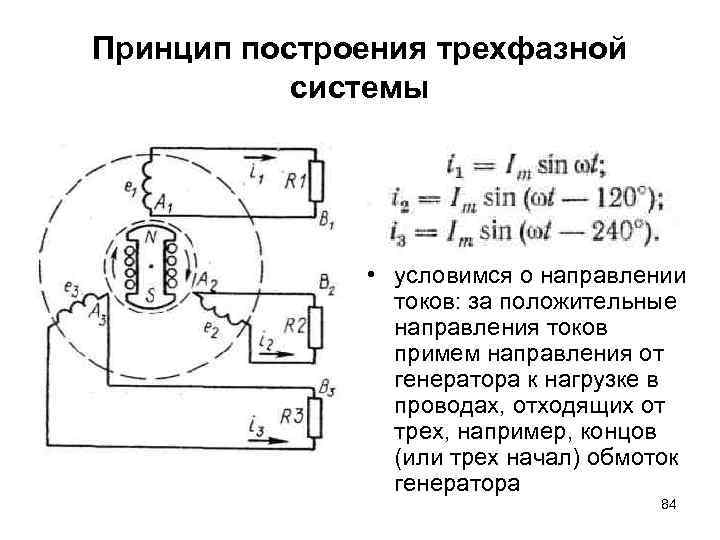Принцип построения трехфазной системы • условимся о направлении токов: за положительные направления токов примем направления от генератора к нагрузке в проводах, отходящих от трех, например, концов (или трех начал) обмоток генератора 84

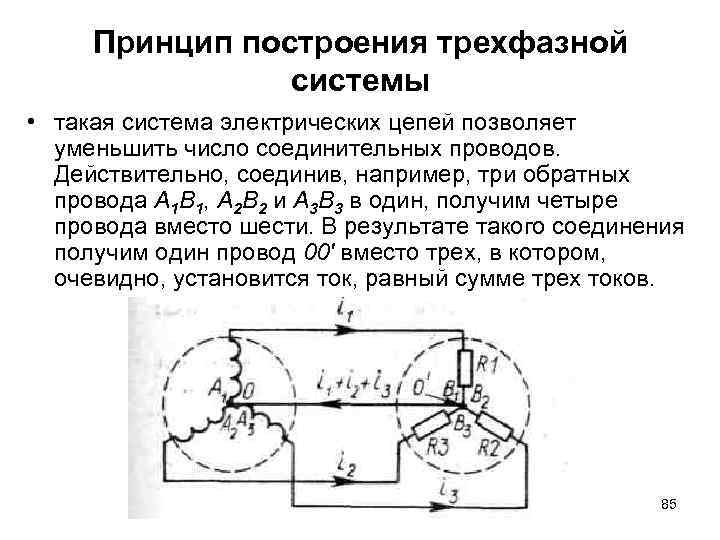Принцип построения трехфазной системы • такая система электрических цепей позволяет уменьшить число соединительных проводов. Действительно, соединив, например, три обратных провода А 1 В 1, А 2 В 2 и A 3 B 3 в один, получим четыре провода вместо шести. В результате такого соединения получим один провод 00' вместо трех, в котором, очевидно, установится ток, равный сумме трех токов. 85

Принцип построения трехфазной системы • Для того чтобы судить о значении тока в проводе 00', найдем его мгновенное значение, сложив мгновенные значения трёх токов • т. е. суммарный ток в проводе 00' равен нулю. • Это же суммирование можно произвести и с помощью векторов 86

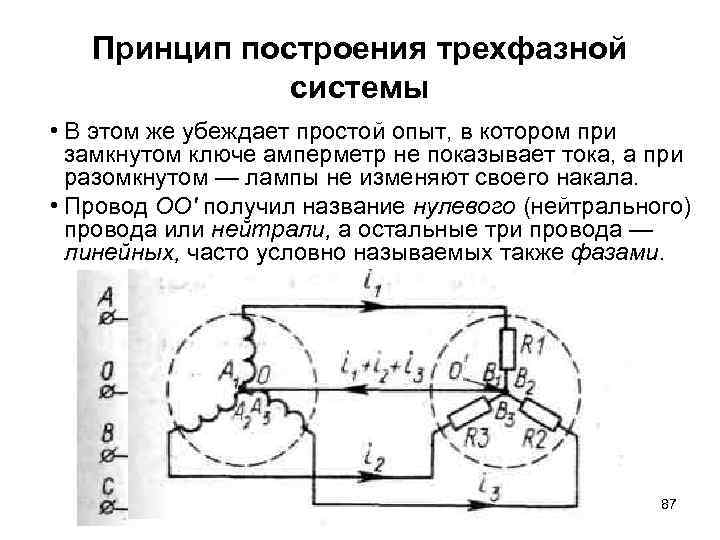Принцип построения трехфазной системы • В этом же убеждает простой опыт, в котором при замкнутом ключе амперметр не показывает тока, а при разомкнутом — лампы не изменяют своего накала. • Провод ОО' получил название нулевого (нейтрального) провода или нейтрали, а остальные три провода — линейных, часто условно называемых также фазами. 87

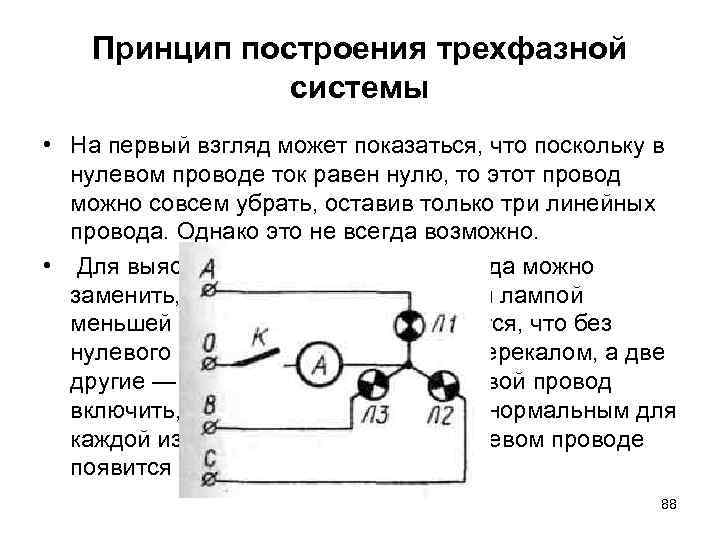Принцип построения трехфазной системы • На первый взгляд может показаться, что поскольку в нулевом проводе ток равен нулю, то этот провод можно совсем убрать, оставив только три линейных провода. Однако это не всегда возможно. • Для выяснения роли нулевого провода можно заменить, например, лампу Л 1 другой лампой меньшей мощности. При этом окажется, что без нулевого провода лампа Л 1 горит с перекалом, а две другие — с недокалом. Если же нулевой провод включить, то лампы будут светиться нормальным для каждой из них накалом, но зато в нулевом проводе появится некоторый ток I 0. 88

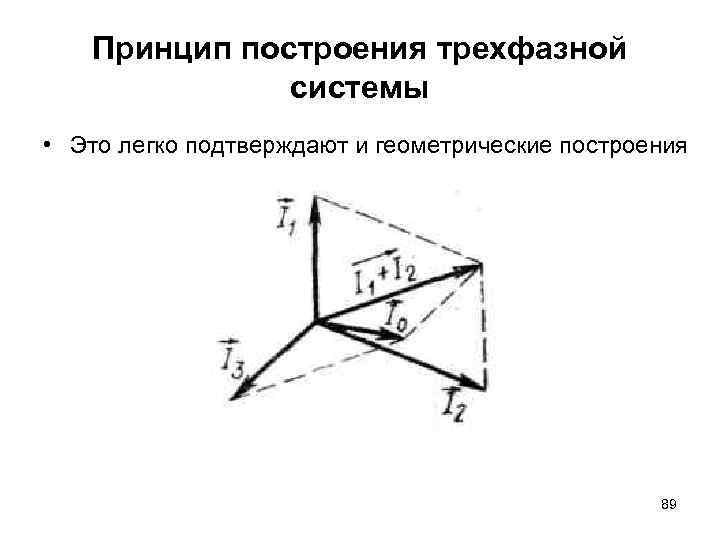Принцип построения трехфазной системы • Это легко подтверждают и геометрические построения 89

Принцип построения трехфазной системы • Следовательно, нулевой провод не нужен в цепях с симметричными нагрузками (с нагрузками равных сопротивлений и вызывающими одинаковый сдвиг по фазе между током и напряжениями). К таким нагрузкам относятся трехфазные двигатели, электрические печи и т. д. Эти линии называют трехпроводными. • Однако наличие нулевого провода обеспечивает постоянство напряжений на элементах несимметричной трехфазной нагрузки. • Ток в нулевом проводе всегда меньше алгебраической суммы токов в фазах и равен их геометрической сумме. 90

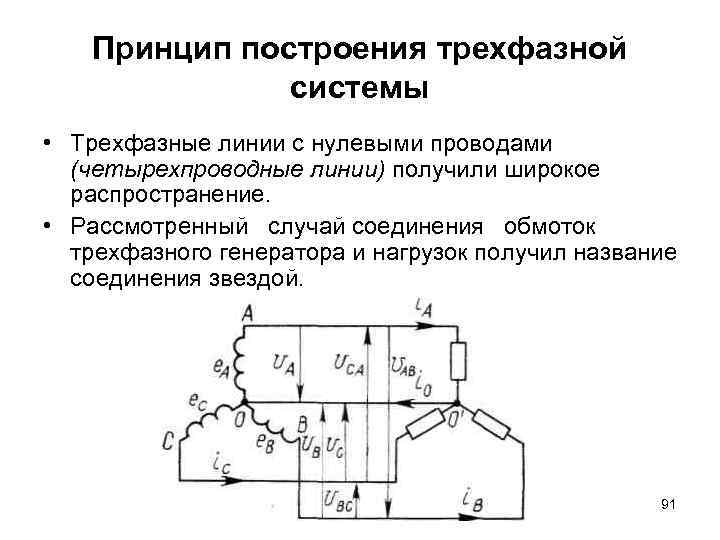Принцип построения трехфазной системы • Трехфазные линии с нулевыми проводами (четырехпроводные линии) получили широкое распространение. • Рассмотренный случай соединения обмоток трехфазного генератора и нагрузок получил название соединения звездой. 91

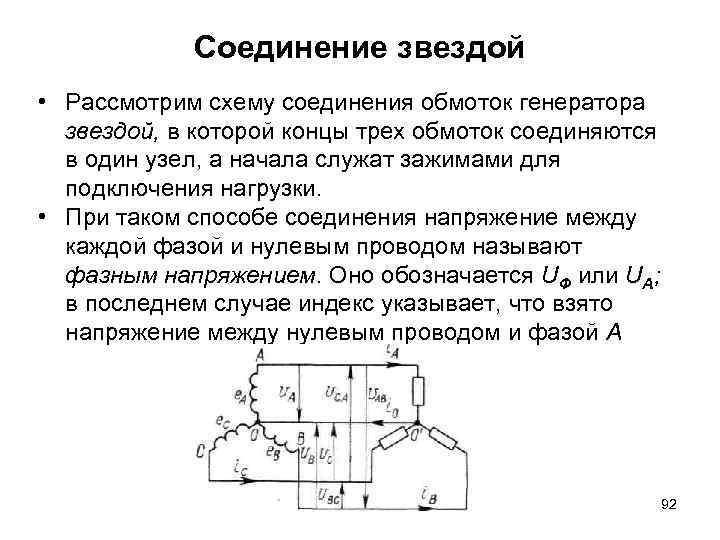Соединение звездой • Рассмотрим схему соединения обмоток генератора звездой, в которой концы трех обмоток соединяются в один узел, а начала служат зажимами для подключения нагрузки. • При таком способе соединения напряжение между каждой фазой и нулевым проводом называют фазным напряжением. Оно обозначается UФ или UA; в последнем случае индекс указывает, что взято напряжение между нулевым проводом и фазой А 92

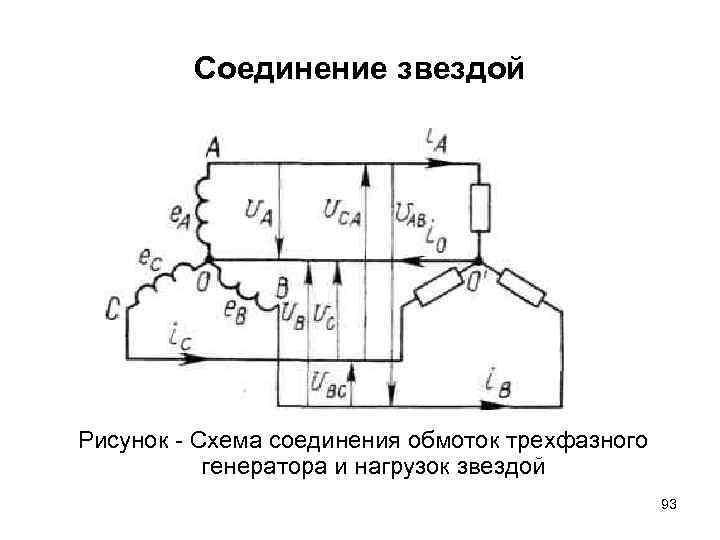Соединение звездой Рисунок Схема соединения обмоток трехфазного генератора и нагрузок звездой 93

Соединение звездой • Напряжения между фазами А — В, В — С и С — А называют линейными. • Они обозначаются UЛ или UAB, UBC и UСA. • Может показаться, что линейное напряжение, например UAB , вдвое больше фазного UA или UВ. Но это не так. • Для определения соотношения между линейным и фазным напряжениями надо брать не алгебраическую сумму фазных напряжений, а их геометрическую разность (разность векторов). 94

Соединение звездой • Линейные напряжения представляют собой разность потенциалов между точками А и В, В и С, С и А. Чтобы определить разность потенциалов, нужно условно выбрать точку, потенциал которой принят за нуль. Такой точкой, вообще говоря, может быть любая (А, В, С или 0). В трехфазных цепях потенциал нулевого провода принимают равным нулю, а провод, как правило, соединяют с землей (заземляют). Тогда потенциалы точек А, В и С будут соответственно UA, UB и UC, а линейные напряжения представляют собой разности потенциалов этих точек 95

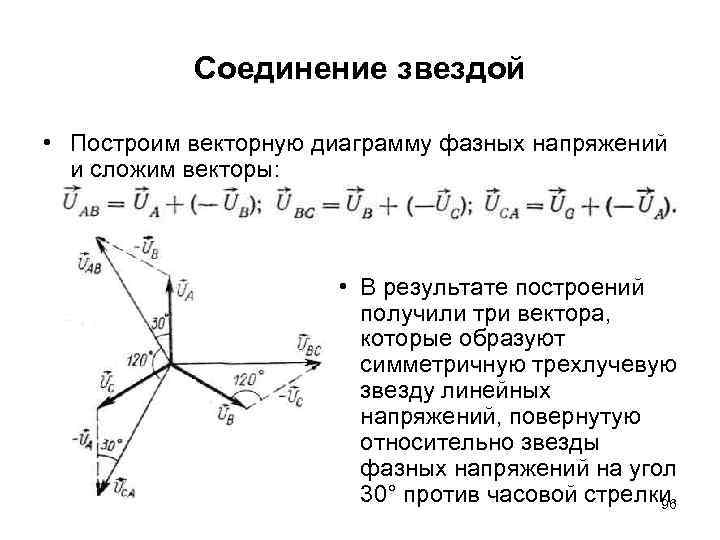Соединение звездой • Построим векторную диаграмму фазных напряжений и сложим векторы: • В результате построений получили три вектора, которые образуют симметричную трехлучевую звезду линейных напряжений, повернутую относительно звезды фазных напряжений на угол 30° против часовой стрелки. 96

Соединение звездой • Для установления соотношения между абсолютными значениями линейного и фазного напряжений рассмотрим тупоугольный треугольник с углом 120° при вершине, образованной, например, векторами UA, — UВ и UAB. Из этого треугольника следует: • Так как для симметричных звезд • то 97

Соединение звездой • откуда • Например, если принять линейное напряжение UЛ = 220 В, то фазное равно • Если же напряжение 220 В принять фазным, то линейное напряжение равно • В соответствии с ГОСТом напряжения 127, 220 и 380 В приняты стандартными для приемников низкого напряжения. 98

Соединение звездой • Однако напряжения, которые создают генераторы электростанций, достигают нескольких киловольт (до 20 к. В), поэтому напряжения 127, 220 и 380 В получают на вторичных обмотках понижающих трансформаторов. • В случае соединения звездой с нейтралью (четырехпроводная линия) в линии существуют две системы напряжений, например 220/127 и 380/220 В. Два напряжения (линейное и фазное) в одной и той же линии — достоинство четырехпроводной линии. • Система 380/220 В является более экономичной, нежели система 220/127 В, так как для электропередачи при одной и той же мощности требуется меньший расход металла на провода за счет меньшего тока. 99

Соединение звездой • История принятия напряжения 127 В (не 120 и не 130 В) в качестве стандартного такова. До ламп накаливания для освещения пользовались дуговыми лампами, которые наиболее спокойно горели при переменном напряжении 55 В. Для двух таких ламп, соединенных последовательно, нужно было 110 В, а для четырех — 220 В. Эти напряжения были приняты еще до изобретения трехфазной системы как стандартные. На них, и в особенности на напряжение 220 В, изготовлялись не только лампы, но и все электрические приборы и машины. Поэтому при внедрении трехфазной системы исходили из наиболее подходящего напряжения — 220 В, при этом фазное напряжение составляет около 127 В. 100

Соединение звездой • Соединение звездой применяют в соединении обмоток трехфазных генераторов, а соединение звездой с нейтралью (четырехпроводная трехфазная линия) — в технике освещения, где осветительные приборы включают, главным образом, на фазное напряжение. Необходимость нулевого провода вытекает из того, что при работе осветительных приборов практически невозможно добиться симметрии нагрузок. В таких сетях все три фазы и нейтраль подводятся, например, к жилым домам, а внутри каждого дома стремятся примерно одинаково загрузить каждую из фаз с тем, чтобы общая нагрузка была более или менее симметричной. При этом к каждой квартире подводится нулевой провод и одна из фаз. На распределительных щитах, через которые проходят две или три фазы, в нулевой провод предохранитель не ставится, так как его перегорание может привести к асимметрии напряжений. 101

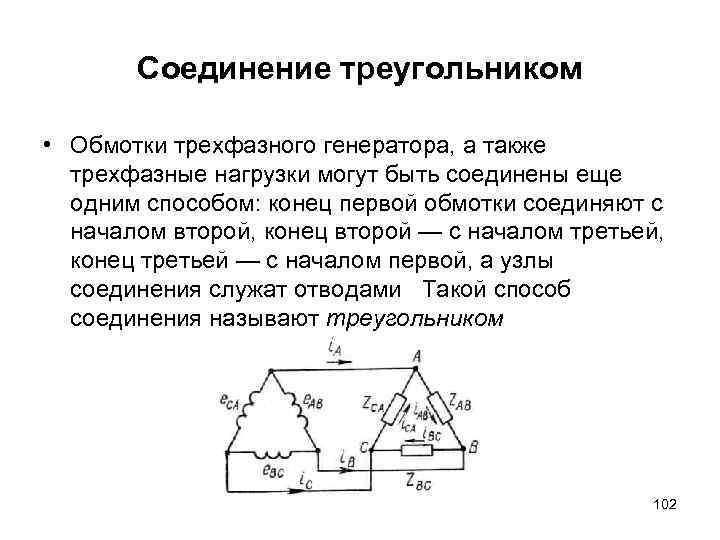Соединение треугольником • Обмотки трехфазного генератора, а также трехфазные нагрузки могут быть соединены еще одним способом: конец первой обмотки соединяют с началом второй, конец второй — с началом третьей, конец третьей — с началом первой, а узлы соединения служат отводами Такой способ соединения называют треугольником 102

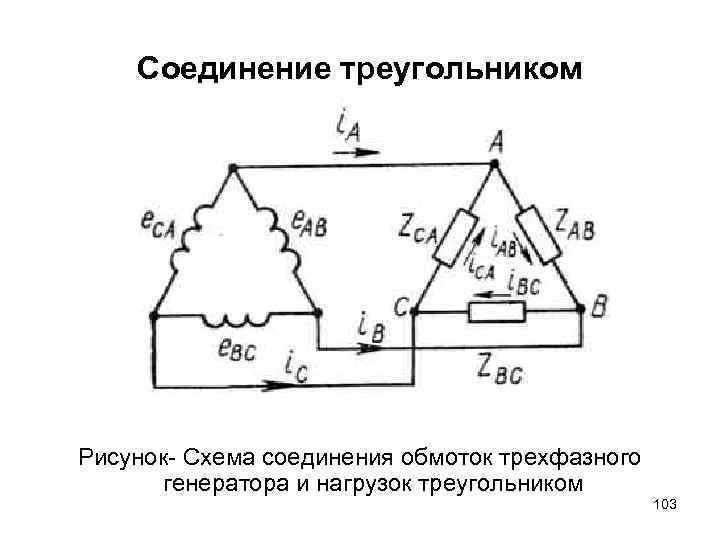Соединение треугольником Рисунок Схема соединения обмоток трехфазного генератора и нагрузок треугольником 103

Соединение треугольником • Кажущегося короткого замыкания в обмотках генератора не произойдет, так как в любой момент времени сумма ЭДС в его обмотках равна нулю: • Ток при отсутствии внешней нагрузки в замкнутом треугольнике также равен нулю. Это справедливо в том случае, если все три ЭДС строго синусоидальны. • В работе генератора форма ЭДС может отклоняться от синусоидальной, поэтому соединение треугольником обмоток генератора, как правило, не применяют. • Однако соединение треугольником широко используется у трехфазных потребителей, создающих 104 симметричную нагрузку (двигатели, печи и т. д. )

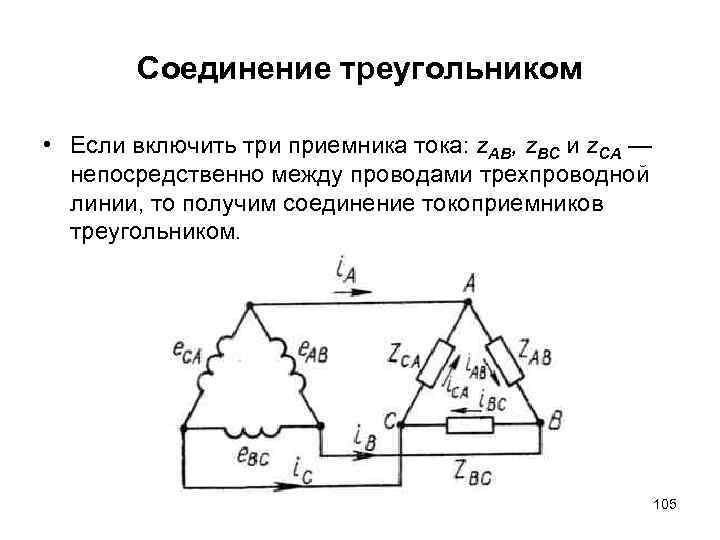Соединение треугольником • Если включить три приемника тока: z. АВ, z. BC и z. СA — непосредственно между проводами трехпроводной линии, то получим соединение токоприемников треугольником. • При таком соединении нет различия между фазным и линейным напряжениями, так как напряжение между началом и концом каждой фазы приемника является в то же время линейным напряжением. • Зато здесь появляется различие между фазными (IАВ, IВС и IСА) и линейными токами (IА, IВ и IC) приемника. 105

Соединение треугольником 106

Мощность трехфазной системы 107