ОСНОВЫ ФИЗИКИ ЗЕМЛИ Введение. Гравитационное поле Земли Лекция

ОСНОВЫ ФИЗИКИ ЗЕМЛИ Введение. Гравитационное поле Земли Лекция 1

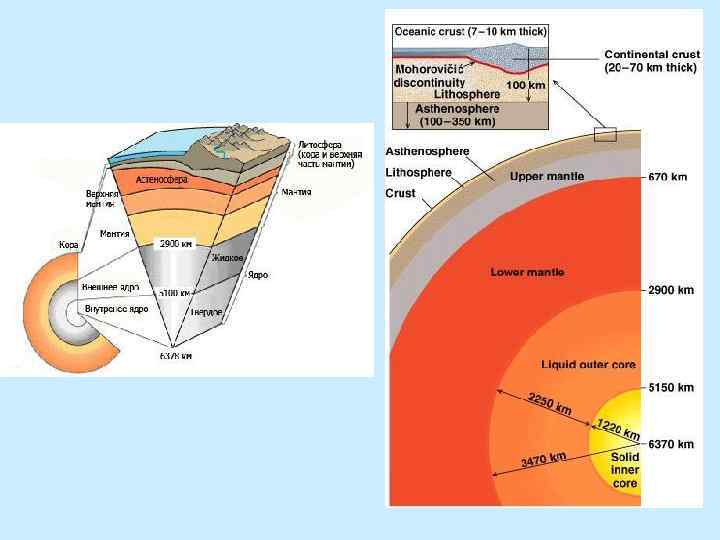
Предмет и методы физики Земли Предметом Физики Земли являются ее внутреннее строение, состояние вещества и динамика планетных недр. Эти три понятия нуждаются в детализации. Изучение внутреннего строения Земли включает ряд тем. 1. Определение параметров ее слоистой структуры по распределению скоростей сейсмических волн v. P и v. S. На этой основе определяются упругие модули сжатия К, сдвига μ, коэффициент Пуассона σ по соотношениям: В этих соотношениях К имеет смысл адиабатического модуля сжатия Кs; ρ – плотность; Ф – сейсмический параметр. 3

2. Оценка распределения плотности ρ в сферически слоистой среде с известным по сейсмологическим данным положением границ раздела скоростей. Для этого привлекаются данные гравиметрии – гармонические моменты: а) масса Земли, определяемая первым членом в разложении гравитационного потенциала по сферическим функциям, при n = 0: J 0 = 1 (это безразмерная масса). б) момент инерции относительно оси вращения С, который определяется по двум величинам: J 2, это второй член разложения гравитационного потенциала (n = 2), и динамическому сжатию Н, оцениваемому по спутниковым измерениям: , где А – момент инерции относительно экваториальной оси; R – экваториальный радиус Земли; 4

в) динамические характеристики Земли периоды и амплитуды нормальных мод собственных колебаний Земли (сфероидальных и крутильных); параметры прецессии, свободной и вынужденной нутации оси вращения Земли, чандлеровских колебаний положения полюса и вариаций скорости вращения (длительности суток). По затуханию объемных волн (изменению амплитуды волн с расстоянием) после исключения эффекта геометрического расхождения волновых фронтов определяется добротность среды Q – характеристика поглощения энергии волн в среде из-за ее неидеальной упругости. Для оценки положения границы литосфере и астеносферы по различию поглощения (добротности среды) используются данные о дисперсии поверхностных волн Лява и Рэлея. Изменение плотности между границами раздела предполагается зависящим только от давления и температуры в 5 условиях гидростатического равновесия.

3. По известной плотностной структуре (r) оценивается распределение давления в недрах Земли в гидростатическом приближении: d. P / dr = g (g – гравитационное ускорение, определенное по известной плотностной модели). 4. Исследование закономерностей распределения физических характеристик в Земле проводится по принципу выделения главной (сферически симметричной) части, чтобы затем выявлять и анализировать аномалии этих свойств в отдельных слоях: v. P(S)(r, , ) = v. P(S)0(r) + v. P(S)(r, , ), (r, , ) = 0(r) + (r, , ). Здесь: v. P(S) – скорости распространения продольных (поперечных) волн, v. P(S)0(r) – сферически симметричная часть скоростной модели Земли, v. P(S) – неоднородности относительно сферически симметричной модели. Обозначения во второй формуле – для распределения плотности – аналогичны. 6

Изучение состояния вещества включает определение термодинамических параметров – давления P, температуры Т, теплоемкости с. Р и др. , коэффициентов переноса – теплопроводности, диффузии, вязкости. Выделяются участки плавления, зоны твердофазных трансформаций вещества. Эти данные являются фактической основой для геодинамического моделирования процессов в Земле. Изучение динамики слоев Земли основывается на распределении геофизических свойств, термодинамических параметров и коэффициентов переноса. Физика Земли предоставляет геодинамике фактическую информацию о среде, выводы из изучения пространственной структуры и вариаций во времени геофизических полей. Практически важными явлениями динамики верхней части земной коры является сейсмичность и вулканизм. 7

Гравитационное поле и фигура Земли Сила тяжести и ее потенциал Силой тяжести называют силу притяжения тела к Земле. Для краткости (и не строго) так называют гравитационное ускорение g, векторную сумму ускорения притяжения по закону Ньютона f и центробежного ускорения из-за вращения Земли P. Закон Ньютона описывает притяжение двух масс m 1 и m 2, разделенных расстоянием r: Если отнести F к единичной массе притягиваемой точки (m 2 = 1), получим напряженность поля с размерностью ускорения (m = m 1 – масса притягивающего тела): . 8

Векторную форму закона Ньютона получим, считая r радиусвектором притягиваемой точки P относительно точки М. Так как сила притяжения направлена от P к M противоположно r, то . В законе Ньютона и всюду далее G − гравитационная постоянная, G = 6, 673· 10− 11 м 3/кг·с2. Обозначения координат: в единой системе (x, y, z) координаты точек определения элементов поля обозначаются как (x, y, z), а координаты притягивающих точек – как (ξ, η, ζ). 9

Модуль r радиус-вектора r в этих обозначениях: направляющие косинусы Проекции g на оси координат gx, gy, gz − это взятые с обратным знаком производные одной функции – потенциала притяжения Потенциал имеет смысл работы поля по перемещению положительной массы из бесконечности в данную точку. 10

Пока речь шла о точечных массах. Земля, все ее оболочки и геологические тела являются объемными. Гравитационное поле аддитивно: притяжение совокупности точечных масс равно сумме отдельных эффектов или интегралу − при непрерывном распределении масс с плотностью σ(ξ, η, ζ). Потенциал притяжения Землей любой внешней точки равен Потенциал притяжения имеет следующие свойства: а) потенциал W и его производные – однозначные, непрерывные и конечные функции координат вне притягивающих масс; б) W − функция, регулярная на бесконечности: lim W = 0; в) вне масс выполняется уравнение Лапласа а в области с массами плотностью σ(ξ, η, ζ) в любой точке справедливо уравнение Пуассона 11

Гравитационное поле Земли слагается из притяжения масс g и центробежного ускорения P из-за вращения вокруг оси. Притяжение g направлено к центру масс Земли. Центробежное ускорение относительно оси вращения P′ = ω2 ρ; ω − угловая частота, ρ – расстояние точки от оси вращения. В координатах (x, y, z) с началом в центре и осью z по оси вращения Ускорение уменьшается на величину P, равную проекции P′ на вертикаль: P = P′cos φ. Так как ro = R cos φ, R − радиус Земли, получаем P = ω2 R cos 2φ. 12

В прямоугольных координатах центробежное ускорение и его составляющие по координатам имеют вид Px = ω2 x; Py = ω2 y; Pz = 0. Введем центробежный потенциал Ω(x, y, z), частные производные которого равны составляющим центробежного ускорения: Очевидно, что Ω = ω2 . Полная величина ускорения силы тяжести есть векторная сумма ускорения притяжения и центробежного ускорения Потенциал силы тяжести равен V = W + Ω: 13

Свойства потенциала силы тяжести V отличаются от свойств потенциала притяжения W тем, что V не является регулярным на бесконечности: при r→∞ V → ∞; и V удовлетворяет уравнениям Пуассона с различными правыми частями: вне масс V = ω2, в области масс V = ω2 − 4π G σ(ξ, η, ζ). Потенциал V − однозначная и непрерывная функция координат, и для него можно ввести понятие поверхностей уровня, т. е. поверхностей с постоянными значениями потенциала: V = const. Приращение потенциала по произвольному направлению l (от одной поверхности с V = C 1 к другой с V = C 2 = C 1 + ∆V) равно Так как ∆x= ∆l cos (l, x); ∆y = ∆l cos (l, y); ∆z = ∆l cos (l, z), а составляющие силы тяжести gx = ∂V/∂x; gy = ∂V/∂y; gz = ∂V/∂z, получаем ∆V = g cos (l, g) ∆l или ∆V / ∆l = gl. 14

Если cos (l, g) = 0 (направление l перпендикулярно силе тяжести), ∆V = 0 и V = const. Это значит, что в точках эквипотенциальной поверхности сила тяжести направлена по нормали к этой поверхности. Значение потенциала V = Ci определяет положение поверхности уровня. На Земле поверхность уровня реального потенциала называется геоидом. Обычно используется геоид, константа для которого выбрана так, чтобы он совпадал с невозмущенной поверхностью океанов. От него ведется отсчет высот земной поверхности. Определение положения этой поверхности на континентах является сложной геодезической задачей. Расстояние между поверхностями уровня по нормали к ним равно ∆n = ∆V / g, что соответствует определению g как градиента потенциала. Сила тяжести направлена в сторону увеличения значений потенциала: g = grad V. 15

Нормальное гравитационное поле Свойства нормального поля имеют прямое отношение к фигуре Земли и для вычисления гравитационных аномалий. Чтобы аномалии можно были связаны с плотностными неоднородностями в Земле, нормальное е поле должно включать: а) влияние масс с зависящей только от радиуса плотностью; б) эффект сжатия Земли; в) вклад центробежного ускорения. Последние два эффекта обусловлены вращением Земли: центробежное ускорение – непосредственно, а сжатие – как результат приспособления фигуры Земли к длительному вращению. В этом процессе вещество Земли ведет себя как вязкая жидкость. Разделить потенциал V или ускорение силы тяжести g на нормальные компоненты − V 0(φ) и γ(φ), и аномальные − T(ρ, φ, λ) и g(ρ, φ, λ) можно двумя путями. 16

1. Задать нормальную плотностную модель Земли, ее ось и скорость вращения и решить прямую задачу для потенциала силы тяжести. В этом подходе важна теорема Стокса: гравитационное поле на поверхности уровня определяется ее формой, а также массой и угловой скоростью вращения планеты и не зависит от распределения плотности по радиусу. 2. Выделить в реальном гравитационном поле его главную часть с простыми закономерностями изменения на земной поверхности. Это достигается гармоническим анализом гравитационного поля, выделением в нем главных гармоник (имеющих наибольшую амплитуду, резко отличающуюся от амплитуд гармоник более высокой степени и порядка). Поскольку построение плотностной модели Земли само является сложной задачей, предпочтителен второй способ. В нем используется разложение гравитационного потенциала в ряд по сферическим функциям – полиномам Лежандра. 17

Гравитационный потенциал в виде ряда по сферическим функциям Потенциал притяжения в точке P(ρ, φ, λ) равен В точке М(ρ1, φ1, λ 1) – элемент массы dm = σ(r 1, φ1, λ 1) dv. В виде ряда нужно представить величину 1 / r. Это функция гармоническая, она является фундаментальным решением уравнения Лапласа. Базисные функции также должны быть гармоническими. Функция 1/r – производящая функция для полиномов Лежандра: Pn (cos γ) − полином Лежандра степени n; n ≥ 0 − целое число. 18

Для cos γ справедлива теорема сложения cos γ = sin φ1 + cos φ1 cos (λ − λ 1). Для Pn (cos γ) известна теорема сложения 19

Подставив это выражение в формулу для 1/r, а результат − в интеграл для потенциала W, получим где σ = σ (ρ1, φ1, λ 1) − распределение плотности; Pnm (sin φ) − присоединенные полиномы Лежандра степени n и порядка m. Обратите внимание: перед интегралами в этом выражении стоят множители с координатами точки Р, в которой определяется поле, а под интегралами − величины с координатами притягивающих масс. 20

Интегралы, зависящие только от распределения масс в Земле, называются постоянными Стокса, . Их обозначения: Постоянные Стокса являются безразмерными величинами; М − масса Земли, R − ее средний радиус. Множители перед интегралами являются нормирующими. Общий вид разложения потенциала притяжения в ряд с использованием коэффициентов Стокса: 21

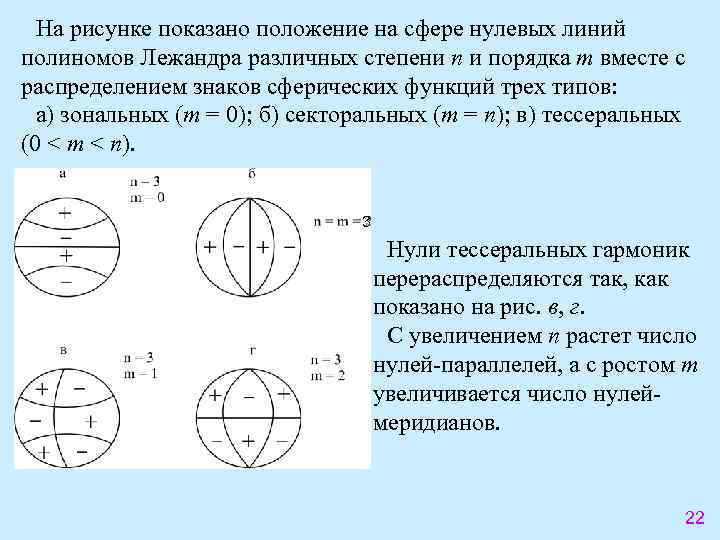На рисунке показано положение на сфере нулевых линий полиномов Лежандра различных степени n и порядка m вместе с распределением знаков сферических функций трех типов: а) зональных (m = 0); б) секторальных (m = n); в) тессеральных (0 < m < n). 3 Нули тессеральных гармоник перераспределяются так, как показано на рис. в, г. С увеличением n растет число нулей-параллелей, а с ростом m увеличивается число нулеймеридианов. 22

В ряд для потенциала силы тяжести нужно добавить потенциал центробежного ускорения: Путем выбора начала и осей координат можно исключить часть первых членов в разложении потенциала притяжения: 1) n = 0: P 0(sin φ) = 1; (R / ρ)0 = 1; σ dv = M; J 0 = 1. Это безразмерная масса. 2) n = 1: P 1(sin φ) = sin φ; P 11(sin φ) = cos φ; . Так как ρ sin φ = ζ, имеем: . Это безразмерная координата центра масс Земли по оси. C 11 и S 11 дают координаты центра масс в плоскости экватора: Т. к. начало координат – в центре Земли (ξ 0 = η 0 = ζ 0 = 0), J 1 = C 11 = S 11 = 0, т. е. слагаемых с n = 1 в разложении нет. 23

3) n = 2: P 2(sin φ) = (3 sin 2 φ − 1)/2; P 21(sin φ) = 3 sin φ cos φ; P 22(sin φ) = 3 cos 2 φ. Из формул для постоянных Стокса получаем: A, B, C – главные моменты инерции относительно осей x, y, z; D, Е, F − главные произведения инерции относительно этих осей. Моменты инерции − это конструкции вида C = ∫(ξ 2 + η 2) σ dv, а произведения инерции − вида F = ∫ ξ η σ dv; A и B аналогичны C; D и E аналогичны F с заменой координат. Если ось z направлена по оси вращения, обращаются в нуль произведения инерции D и Е, т. е. С 21 = S 21 = 0. Применительно к телу вращения F = 0 и A = B, т. е. S 22 = 0 и C 22 = 0; в разложении остается только слагаемое, которое определяется разностью моментов инерции C и A: 24

Относительная разность этих моментов инерции называется динамическим сжатием Н: До эпохи спутников динамическое сжатие определялось по параметрам прецессии и неравенствам в движении Луны. Разные методы давали значения Н от 1/305, 51 до 1/296, 7. В настоящее время на два порядка более точные оценки получаются на основе изучения орбит спутников. По величинам J 2 и Н оценивается момент инерции С относительно оси вращения Это главная характеристика распределения плотности внутри Земли; J 2 / H = 0, 33078; для однородного шара она равна 0, 4. Кроме J 2 по спутниковым данным оцениваются моменты более высокого порядка J 3, J 4, J 6, которые являются интегралами от распределения произведения плотности на соответствующую степень радиуса ρ. 25

Изучение структуры гравитационного поля Земли сравнением амплитуд гармоник (с разными значениями степени n и порядка m) показало, что нормальную модель Земли можно представить эллипсоидом вращения. Отклонения от него в экваториальном сечении (трехосность) не больше других отклонений геоида от эллипсоида вращения. Итак, потенциал силы тяжести Земли, состоящий из потенциала притяжения и потенциала центробежного ускорения с учетом смысла коэффициента J 2 имеет вид Первое слагаемое после раскрытия квадратных скобок это потенциал шара с массой М, равной массе Земли, в точке с текущим радиусом ρ. Второй член обусловлен сжатием Земли, последний − центробежным ускорением. 26

Вторую гармонику потенциала силы тяжести представим в виде Эта величина зависит от широты; она единственная переменная составляющая нормального гравитационного поля. Третье слагаемое в квадратных скобках (с двойной суммой) − это аномальный гравитационный потенциал Т: Для описания центробежной составляющей нормального потенциала вводится константа q – отношение центробежного ускорения к значению силы тяжести на экваторе: где R − средний экваториальный радиус Земли. Нормальный потенциал Vo с этим обозначением равен 27

Для потенциала Vo можно определить поверхность уровня ρ(φ), на которой Vo = const. Эту константу (C) зададим как значение потенциала в точке на экваторе (φ = 0), в которой реальный радиус ρ и средний экваториальный радиус R равны между собой и экваториальной полуоси эллипсоида а: ρ = R = a. При этих условиях получаем Приравняв эту формулу к предыдущей, получим ρ / a. Оно сложное; его представляют рядом по малому параметру (3 J 2 / 2 + q / 2); J 2 = 1, 08264· 10− 3, q = 3, 4614· 10− 3. Если удерживаются члены с малыми первого порядка, получаем формулу Клеро Это уравнение эллипсоида вращения со сжатием α: a и с − экваториальная и полярная полуоси. 28

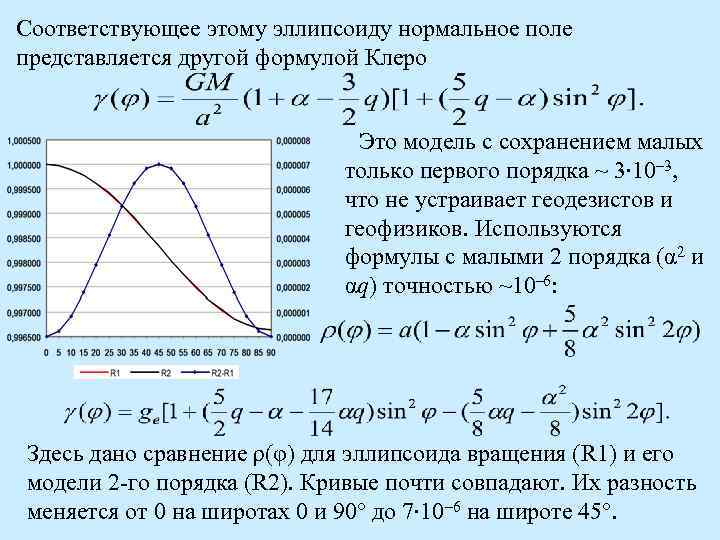Соответствующее этому эллипсоиду нормальное поле представляется другой формулой Клеро Это модель с сохранением малых только первого порядка ~ 3∙ 10– 3, что не устраивает геодезистов и геофизиков. Используются формулы с малыми 2 порядка (α 2 и αq) точностью ~10– 6: Здесь дано сравнение ρ(φ) для эллипсоида вращения (R 1) и его модели 2 -го порядка (R 2). Кривые почти совпадают. Их разность меняется от 0 на широтах 0 и 90° до 7∙ 10– 6 на широте 45°.

Экваториальное значение силы тяжести Оно меньше притяжения шара радиуса a. В модели World Geodetic System-1984 α = 1/298, 25722 = 3, 35281· 10− 3; уравнение эллипсоида вращения имеет выражение (в метрах) ρ(φ) = 6378139, 0 (1 − 0, 0033528 sin 2φ + 0, 000007 sin 22φ). Нормальное поле Earth Gravity Model-1996 для α = 1/298, 25722: γ(φ) = 978032, 53(1 + 0, 0052576 sin 2 φ − 0, 0000058 sin 2 2φ). Разность полярного и экваториального значений нормального ускорения силы тяжести gp − ge = 5, 2 Гл. Изменение радиуса дает 6, 2 Гл, эффект центробежного ускорения 3, 5 Гл, эффект перераспределения масс вследствие сжатия − 4, 5 Гл. Сжатие имеет вклады разных знаков, их сумма 1, 7 Гл – вдвое меньше влияния центробежного ускорения.

Концепция аномалий требует исключения масс, которые не являются объектами изучения. В задачах геологии объекты – плотностные неоднородности; региональные неоднородности – причина аномалий высот геоида, а локальные – помехи в решении задачи. В любом случаи массы, образованные рельефом земной поверхности, полезными объектами не являются. Их влияние нужно исключить. Конструирование масс, подлежащих исключению, называется регуляризацией нормальной модели Земли. Обе процедуры − приведение и регуляризация – решают редукционную проблему. Система поправок для получения аномалий данного вида называется редукцией силы тяжести. Редукционная проблема сначала возникла в геодезической гравиметрии. Это нашло отражение в трактовке смысла редукций в учебной и справочной литературе по гравиразведке, хотя геодезические и геологические требования к гравитационным аномалиям различны.

Принципы гравитационных измерений Поверхность уровня геопотенциала в океанах измеряется методом спутниковой альтиметрии: по положению спутника в геоцентрических координатах лазерной локацией уровня океана вычисляются высоты геоида над эллипсоидом. Используются спутниковые методы измерения полей Земли и других планет. Основной − измерения параметров орбит спутников по данным станций слежения. Параметры изменяются из-за неоднородности гравитационного поля. В методе двух спутников вместе с данными об орбитах используются данные непрерывных измерений расстояния между этими спутниками. Для изучения гравитационных полей других планет применяются измерения лучевых скоростей спутника; используется допплеровский сдвиг частоты радиоисточника на спутнике при изменении проекции вектора его скорости на направление луча от спутника к станции на Земле.

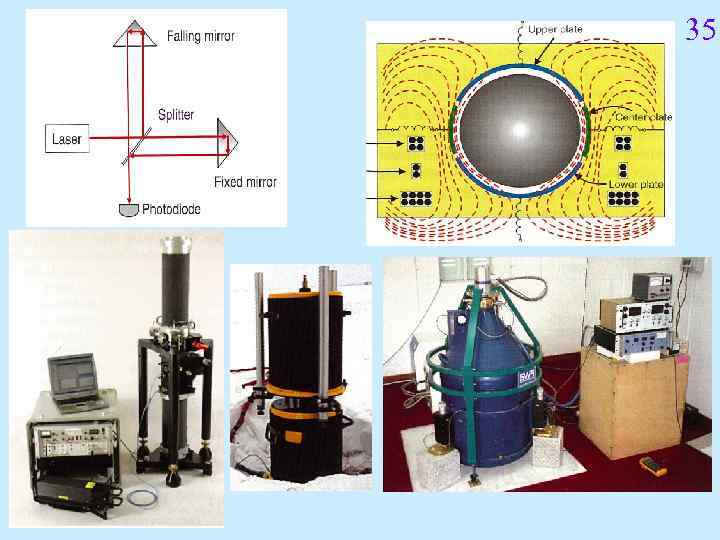
Измерение гравитационного ускорения 33 Методы, основанные на изучении движения тел в поле силы тяжести или изменения частоты колебаний, называются динамическими. Методы, в которых изучается равновесие пробной массы в поле силы тяжести называются статическими. Сила или ее момент сравниваются с силами или моментами сил иной природы: упругости пружин и нитей подвеса и др. Для определения гравитационных аномалий нужно знать абсолютные значения g. Если они получаются в каждом измерении, это абсолютные измерения g. Методы таких измерений сложнее методов относительных измерений, поэтому их применяют в главных опорных пунктах. Абсолютный метод свободного падения реализован в баллистических лазерных гравиметрах. Другие данные получают относительными измерениями приращения (∆g) значений ускорения в пунктах относительно опорных пунктов с известными значениями g.

Для абсолютных измерений используют динамические методы, в которых характеристики движения пробной массы измеряются с требуемой точностью. 34 В настоящее время это возможно только для метода свободного падения. Относительные измерения ∆g можно выполнять как динамическими, так и статическими методами. Используется много систем гравиметров, различных по принципам действия, характеристикам и условиям работы. В геологических задачах важны пространственные неоднородности гравитационного поля. Исключением являются задачи изучения перемещений масс по изменениям силы тяжести во времени, например, в контроле разработки газовых залежей, режима эксплуатации подземных газохранилищ, прогнозе оползней.

35