Основы физики Земли Лекция 2 Фигура Земли Вращение

Основы физики Земли Лекция 2 Фигура Земли. Вращение Земли

Фигура Земли Нормальное гравитационное поле определяет важнейший геодезический параметр нормальной фигуры Земли – сжатие эллипсоида. Этот параметр геодинамическое значение. Сжатие Земли – результат приспособления ее формы к вращению. Его значение зависит от скорости вращения и механических свойств материала. Сжатие во взаимодействием с приливным влиянием Луны усложняет режим вращения Земли. Понятие «нормальная фигура» трактуется как фигура равновесия вращающейся жидкой планеты. Такой фигурой является сфероид Клеро Если плотность изменяется по радиусу, то и сжатие является функцией радиуса; сжатие границы ядра с мантией меньше, чем сжатие поверхности эллипсоида. 2

Поверхность эллипсоида Клеро не строго эквипотенциальная, но с точностью до сжатия (~3· 10– 3). Эллипсоид второго приближения эквипотенциальный с точностью 10– 5. Можно считать, что с такой же точностью эллипсоид находится в гидростатическом равновесии. Эти отклонения от гидростатики могут существовать длительное время, порядка 107 лет. В реальной Земле они обеспечиваются длительной прочностью материала или реализуются в конвективных течениях с соответствующим характерным временем. У вращающейся планеты должны быть: а) северное и южное полушария одинаковы; б) нечетные моменты в разложении потенциала притяжения равны нулю; в) четные моменты убывать как αn (n – степень гармоники). Эти условия выполняются на уровне точности 10– 5 3

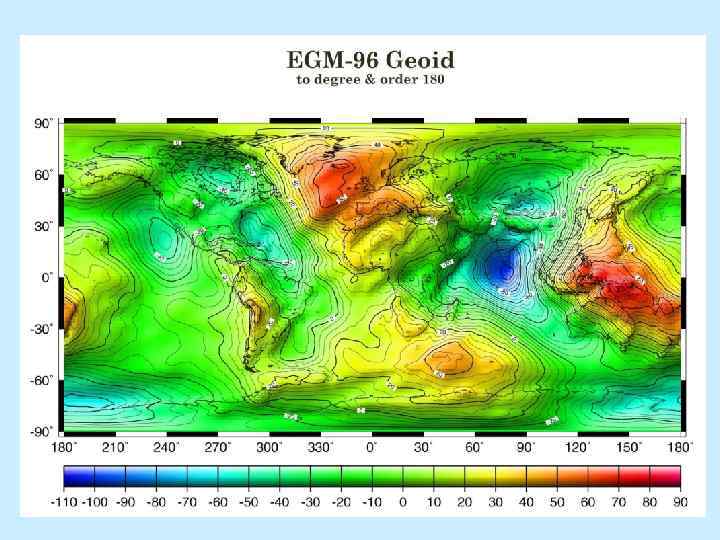
Гравитационные аномалии и высоты геоида Аномалиями ∆g называются отклонения реального гравитационного поля g от нормального поля γ: ∆g = g − γ. Однако g и γ относятся к разным точкам. g измеряется на поверхности Земли, иногда в толще воды, на дне, в скважинах, в шахтах, над земной поверхностью. Значения γ определены на поверхности сфероида. Разность высот между ними определяется высотой точки наблюдения над геоидом (уровнем моря) h и высотой геоида над сфероидом ζ. Эта величина – вторая главная характеристика фигуры Земли, и ее оценка в функции координат ζ(φ, λ) является важной задачей геодезической гравиметрии. Различие высоты точек измерения и их проекций на эллипсоид в условиях большого вертикального градиента силы тяжести вызывает необходимость приведения g и γ в одну точку: или g к поверхности сфероида, или γ в точку измерения g. 4

Перед гравиметрией в геодезии стоит задача определения фигуры Земли: сжатия α, высот геоида ζ. Сжатие оценивается по величине J 2. Высоты геоида определяются отношением аномального потенциала Т к нормальной силе тяжести γ − формулой Брунса По этой формуле нельзя вычислить ζ, так как Т не измеряется. Конструктивной является формула Стокса где ∆g − аномалии силы тяжести, S(φ) − функция Стокса. Геодезические требования к аномалиям: 1) аномалии заданы на геоиде; 2) вне геоида нет притягивающих масс; 3) редукция не изменяет массу Земли; 4) аномалии можно было интерполировать. 5

Чтобы аномалии можно было считать заданными на геоиде, в измеренные значения g вводят поправку за высоту ∆gh = Vzz h. Реальное значение градиента Vzz неизвестно до обработки результатов гравиметрической съемки. Для вычисления поправки за высоту используются нормальные значения для сфероида : где α − сжатие сфероида, φ − широта; или в модели шара: Аномалии силы тяжести, вычисленные с поправкой за высоту, но без учета масс рельефа, называются аномалиями Фая: 7

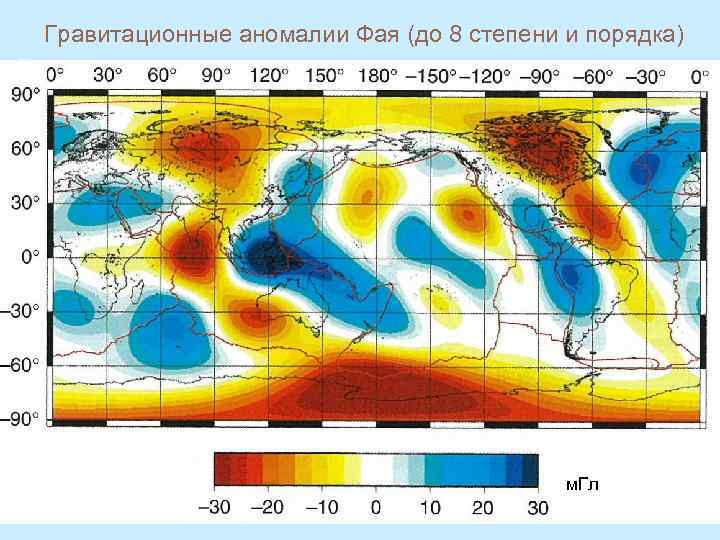Гравитационные аномалии Фая (до 8 степени и порядка) м. Гл

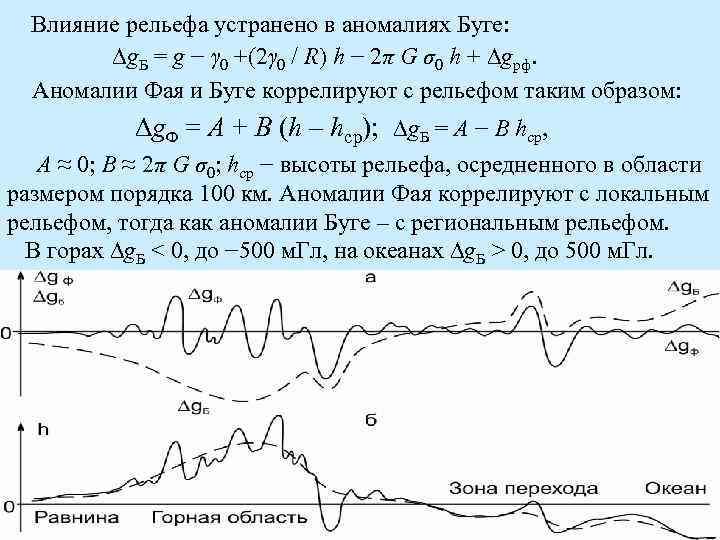Влияние рельефа устранено в аномалиях Буге: ∆g. Б = g − γ 0 +(2γ 0 / R) h − 2π G σ0 h + ∆gрф. Аномалии Фая и Буге коррелируют с рельефом таким образом: ∆g. Ф = A + B (h – hср); ∆g. Б = A − B hср, A ≈ 0; B ≈ 2π G σ0; hср − высоты рельефа, осредненного в области размером порядка 100 км. Аномалии Фая коррелируют с локальным рельефом, тогда как аномалии Буге – с региональным рельефом. В горах ∆g. Б < 0, до − 500 м. Гл, на океанах ∆g. Б > 0, до 500 м. Гл.

В аномалиях Фая есть влияние рельефа, но в среднем поле близкое – на континентах и океанах. В аномалиях Буге эффект рельефа исключен, но аномалии в среднем близки к поправке 2π G σ0 h , как будто эта поправка лишняя, а массы рельефа почти не влияют на гравитационное поле. Это связано с изостатической компенсацией масс рельефа глубинными плотностными неоднородностями другого знака в земной коре и под ней. Аномалии относятся к точкам измерения на высоте h над геоидом, который имеет высоту ζ относительно сфероида. Поскольку высота геоида изменяется от − 80 до 105 м, а длины волн геоида измеряются тысячами километров, влияние высот геоида в геологической гравиметрии мало, поправка Брунса (2γ 0 / R) ζ не учитывается. При GPS-измерениях высоты отсчитываются от эллипсоида.

Изостазия; изостатические аномалии Явление изостазии известно с XVIII в. по работам М. Босковича и П. Буге в Южной Америке, сэра Эвереста, Дж. Эри и Дж. Пратта в Индии, обнаруживших недостаток масс под Андами и Гималаями. А. Гипотеза Пратта: Массы компенсации распределены до уровня Т С плотностью Б. Гипотеза Эри: Блоки коры с постоянной плотностью σк погружены на глубину ΔHi, пропорциональную высоте рельефа hi. Массы компенсации образованы структурой нижней границы коры НМ:

В любых моделях изостазия предполагается полной, локальной: каждый элемент рельефа уравновешен независимо от размеров массами, расположенными под ним. Есть вариант Венинг-Мейнеса гипотезы Эри, учитывающий региональность изостазии – ввиду нереальности компенсации малых масс рельефа. Такие разные распределения компенсационных масс вызывали вопросы: какая из моделей соответствует реальной структуре земной коры; какие тектонические процессы могли образовать ту или другую равновесную структуру земной коры? Дискуссии были бурными; важно, что в их ходе были предложены методы изучения изостазии, имеющие значение и в настоящее время. Тектоническое значение изостатических гипотез Пратта, Эри и др. теперь понимается как регулирующая роль гравитационных сил в геологических процессах.

Формы рельефа менее 50 км не уравновешиваются независимо. Высоты крупных форм рельефа много меньше их горизонтальных размеров: работает формула ∆gпс = 2π G σ H. Равенство топографических и компенсационных масс означает близость их гравитационных эффектов. Для вычисления изостатических поправок не обязательны модели компенсационных масс. Можно построить изостатическую модель в виде гравитационных эффектов компенсационных масс, используя формулу плоского слоя, что реализовано де Грааф-Хантером: ∆g. Г-Х = g − γ 0 +(2γ 0 / R) h − 2π G σ0 h + ∆gрф + 2π G σ0 hср. Формулу можно переписать: ∆g. Г-Х = g − γ 0 +(2γ 0 / R) h − 2π G σ0 (h – hср) + ∆gрф. В этих аномалиях устранена корреляция с локальным рельефом, такая как в аномалиях Фая, и с осреденным рельефом, как в аномалиях Буге. Это свойство аномалий де Грааф-Хантера ставит их в ряд изостатических.

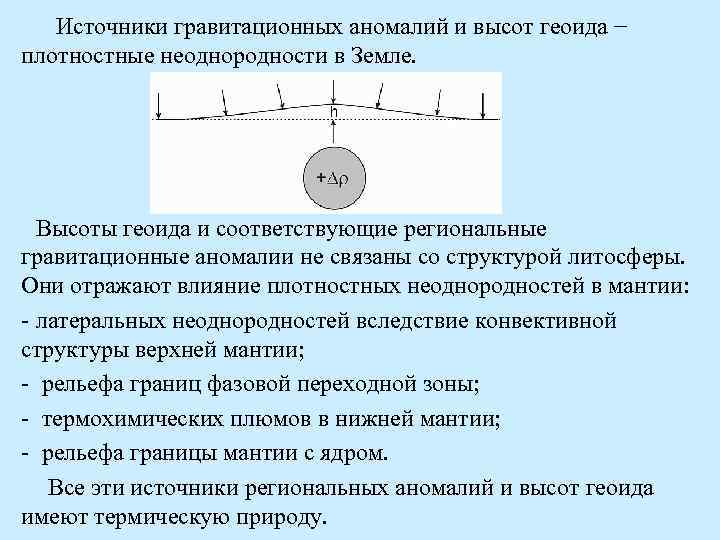Источники гравитационных аномалий и высот геоида − плотностные неоднородности в Земле. Высоты геоида и соответствующие региональные гравитационные аномалии не связаны со структурой литосферы. Они отражают влияние плотностных неоднородностей в мантии: - латеральных неоднородностей вследствие конвективной структуры верхней мантии; - рельефа границ фазовой переходной зоны; - термохимических плюмов в нижней мантии; - рельефа границы мантии с ядром. Все эти источники региональных аномалий и высот геоида имеют термическую природу.

Земные приливы Изменения гравитационного поля во времени по своей природе и пространственно-временным характеристикам четко подразделяются на два класса. 1. Периодические приливные вариации гравитационного поля на Земле из-за ее вращения в поле притяжения Луны и Солнца, изменяющегося при их перемещениях относительно Земли. 2. Вековые вариации гравитационного поля разной природы: вследствие геодинамических процессов в недрах Земли, движений литосферы, землетрясений, извержений вулканов, карстовых и оползневых явлений, изменений уровня грунтовых вод и других приповерхностных процессов, в том числе техногенной природы. 15

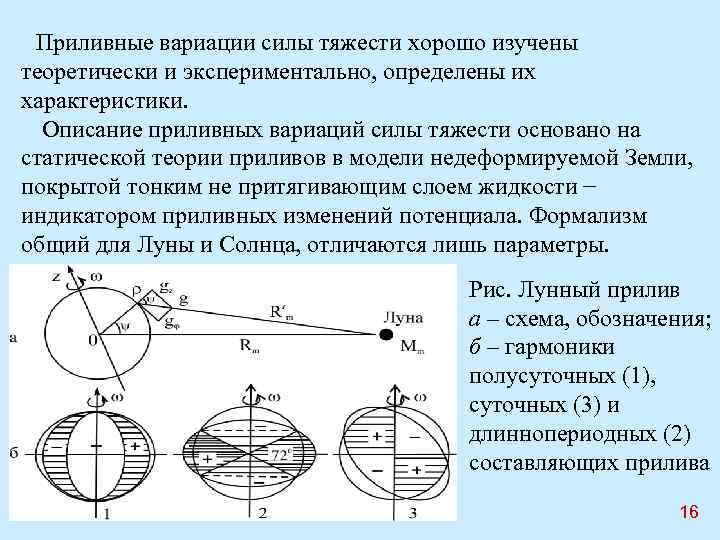Приливные вариации силы тяжести хорошо изучены теоретически и экспериментально, определены их характеристики. Описание приливных вариаций силы тяжести основано на статической теории приливов в модели недеформируемой Земли, покрытой тонким не притягивающим слоем жидкости − индикатором приливных изменений потенциала. Формализм общий для Луны и Солнца, отличаются лишь параметры. Рис. Лунный прилив а – схема, обозначения; б – гармоники полусуточных (1), суточных (3) и длиннопериодных (2) составляющих прилива 16

Радиальная и широтная составляющие притяжения Луной точки на поверхности Земли равны Масса и расстояния с индексом M относятся к Луне, эти индексы для углов опущены; для Солнца используется индекс S. В центре масс Земли (0) эффекты определяют движение Земли как целого в поле тяготения Луны. Приливы вызваны разностями поля в точках P и центре Земли: Получаем, после замены переменных по формулам RM'2= RM 2 + r 2 − 2 r RM cos ψ; RM' sin ψ '= RM ψ; RM' cos ψ '= RM cos ψ − r : 17

Или в другой форме: Как видим, приливный эффект Луны более чем вдвое превышает влияние Солнца, что объясняется много меньшим расстоянием Луны от Земли. Составляющие приливообразующей силы являются производными по радиусу и широте приливного потенциала W 2: Суммарный приливный потенциал W 2 = W 2 M 2 + W 2 S 2. Зенитные расстояния ψ неудобны, их заменяют: геоцентрическая широта φ, склонение Луны и Солнца δM и δS, часовой угол τ для учета вращения Земли. Они связаны с ψ формулой, одинаковой для Луны и Солнца: cos ψ = sin φ sin δ + cos φ cos δ cos τ. 18

После подстановки и преобразований имеем: Для Солнца формула аналогична. В этой формуле g − земное ускорение в точке определения W 2; M − масса Земли. Три слагаемых в этой формуле различаются пространственной и временной структурой: первое − секторальная гармоника P 22(sinφ) с полусуточным периодом; второе − тессеральная гармоника P 21(sin φ) с суточным периодом; третье − зональная гармоника P 2(sin φ), не связанная с часовым углом; ее полумесячный (и для Солнца – полугодовой) период определяется периодичностью изменений склонения δM (и δS). 19

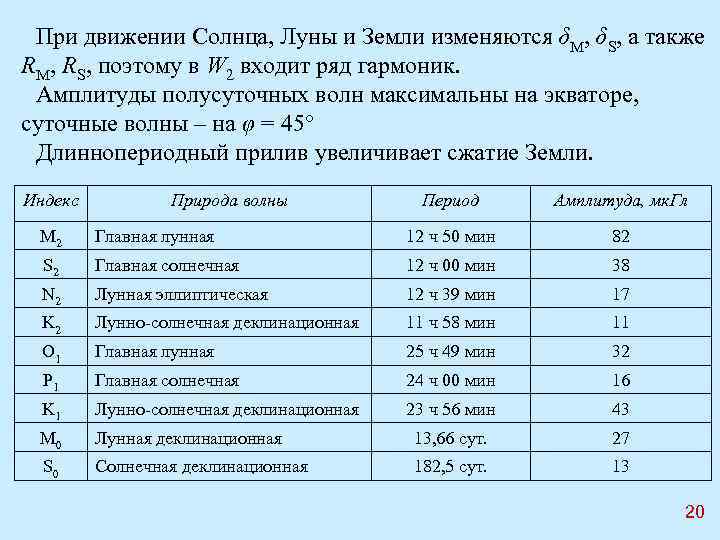При движении Солнца, Луны и Земли изменяются δM, δS, а также RM, RS, поэтому в W 2 входит ряд гармоник. Амплитуды полусуточных волн максимальны на экваторе, суточные волны – на φ = 45° Длиннопериодный прилив увеличивает сжатие Земли. Индекс Природа волны Период Амплитуда, мк. Гл M 2 Главная лунная 12 ч 50 мин 82 S 2 Главная солнечная 12 ч 00 мин 38 N 2 Лунная эллиптическая 12 ч 39 мин 17 K 2 Лунно-солнечная деклинационная 11 ч 58 мин 11 O 1 Главная лунная 25 ч 49 мин 32 P 1 Главная солнечная 24 ч 00 мин 16 K 1 Лунно-солнечная деклинационная 23 ч 56 мин 43 M 0 Лунная деклинационная 13, 66 сут. 27 S 0 Солнечная деклинационная 182, 5 сут. 13 20

Приливные силы деформируют Землю. Эти деформации выражаются через безразмерные коэффициенты − числа Лява k, h, число Шида l. Их определение: h − отношение высоты прилива на упругой Земле к высоте статического теоретического прилива, h = ζ / ζ 0; k − отношение добавочного потенциала, обусловленного перераспределением масс при деформации Земли, к теоретическому потенциалу, k = W 2' / W 2; l − отношение горизонтальных смещений на фронте приливной волны − реального к теоретическому, l = ξ / ξ 0. На упруго деформируемой Земле 1 + h − 3 k/2 = δ, отношение реальных приливных вариаций к их значениям в модели статического прилива. δ определяется по результатам наблюдений приливных вариаций силы тяжести. По данным о наклонах определяется γ: γ = 1 + k − h. По деформациям оценивается l: l = 1 + k − l. 21

По многим приливным обсерваториям, где имеется комплекс гравиметрических, наклономерных и деформографических измерений, получены следующие значения факторов: δ = 1, 16 ± 0, 03; γ = 0, 70 ± 0, 02; l = 1, 25 ± 0, 05, что дает для чисел Лява и Шида средние значения h = 0, 60 ± 0, 05; k = 0, 30 ± 0, 04; l = 0, 05 ± 0, 03. Обнаружена пространственная зональность в распределении на Земле приливных характеристик; имеются данные об их изменениях во времени в связи с землетрясениями. Параметры приливных деформаций Земли интегрально связаны распределением в Земле упругих модулей и плотности. Это позволяет использовать результаты наблюдений земных приливов для независимой проверки физических моделей Земли, построенных на основе сейсмологических данных. 22

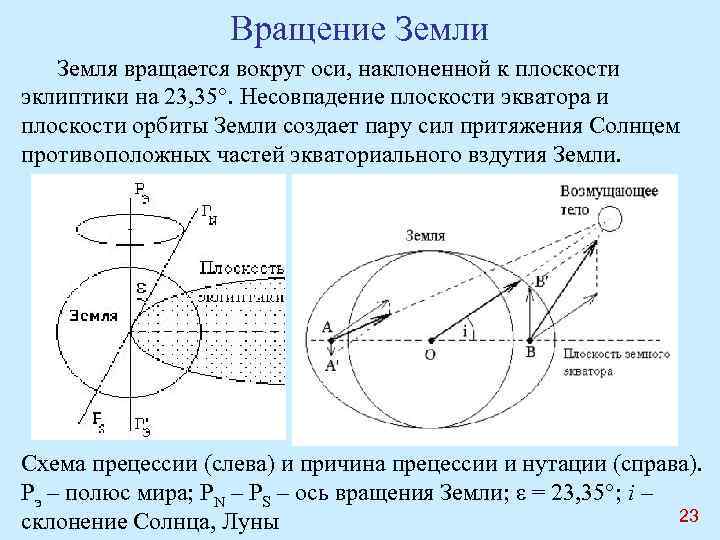Вращение Земли Земля вращается вокруг оси, наклоненной к плоскости эклиптики на 23, 35°. Несовпадение плоскости экватора и плоскости орбиты Земли создает пару сил притяжения Солнцем противоположных частей экваториального вздутия Земли. Схема прецессии (слева) и причина прецессии и нутации (справа). Рэ – полюс мира; РN – PS – ось вращения Земли; ε = 23, 35°; i – 23 склонение Солнца, Луны

24

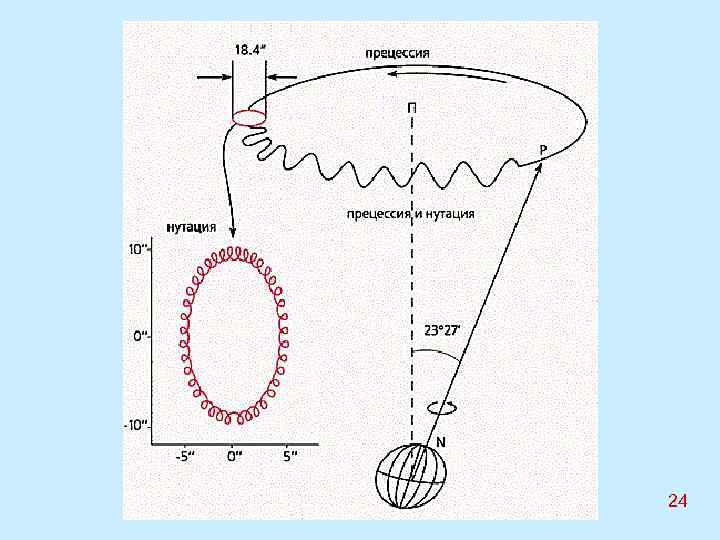
Это приводит к прецессии оси вращения Земли с периодом 25 800 лет и свободной нутации с периодом 306 суток. Изменение склонения Луны приводит к вынужденной нутации с периодом 18, 6 года – время обращения узлов орбиты Луны; а лунный апогей-перигейный период составляет 27, 62 суток. Эти движения – вместе с Землей. Колебания оси в теле Земли и периодические движения полюса по земной поверхности обнаружены по астрономическим наблюдениям широт наземных пунктов. Выделены периоды: 1 год и чандлеровский 410– 435 суток, их сумма дает период биений 6, 8 лет. Главная причина этих колебаний – отклонение оси главного (наибольшего) момента инерции от оси вращения. Они ликвидируют это несоответствие. Момент инерции изменяется при перемещении масс: в атмосфере (из-за сезонных изменений атмосферного давления), на поверхности (ледники, землетрясения) и внутри Земли. 25

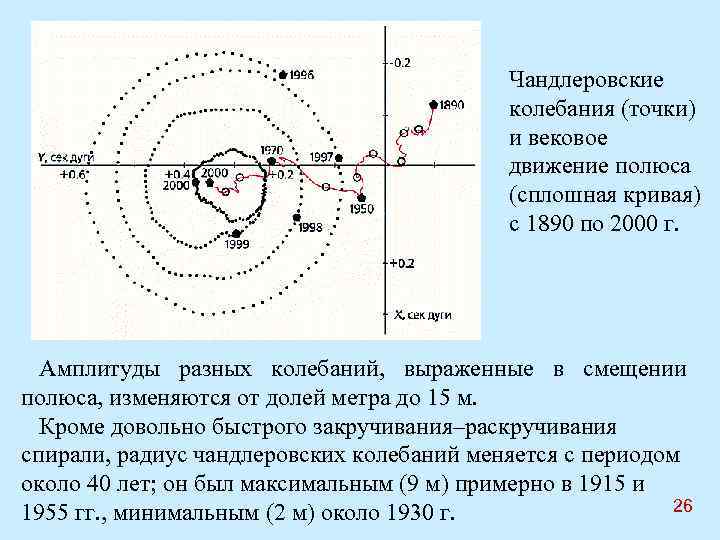Чандлеровские колебания (точки) и вековое движение полюса (сплошная кривая) с 1890 по 2000 г. Амплитуды разных колебаний, выраженные в смещении полюса, изменяются от долей метра до 15 м. Кроме довольно быстрого закручивания–раскручивания спирали, радиус чандлеровских колебаний меняется с периодом около 40 лет; он был максимальным (9 м) примерно в 1915 и 26 1955 гг. , минимальным (2 м) около 1930 г.

Скорость вращения Земли Об изменениях скорости вращения Земли наиболее просто судить по отклонению d. P длительности земных суток от эталонных (86400 с). Чем быстрее движется Земля, тем короче земные сутки. С начала XVIII до середины XIX в. скорость вращения Земли менялась мало, а со второй половины XIX в. и по настоящее время отмечаются нерегулярные флуктуации скорости вращения Земли с периодом 60– 70 лет. Быстро Земля вращалась около 1870 г. (длительность суток была короче на 0, 003 с), медленно около 1903 г. (сутки были длиннее на 0, 004 с). С 1903 по 1934 г. вращение Земли ускорялось, с конца 30 -х годов до 1972 г. замедлялось, а начиная с 1973 г. Земля снова ускоряет свое вращение. Колебание скорости вращения Земли, наблюдавшееся в XX в. с 1903 по 1972 г. , часто считают 60 -70 летним; в XIX в. колебание примерно того же периода относится к 1845 -1903 гг.

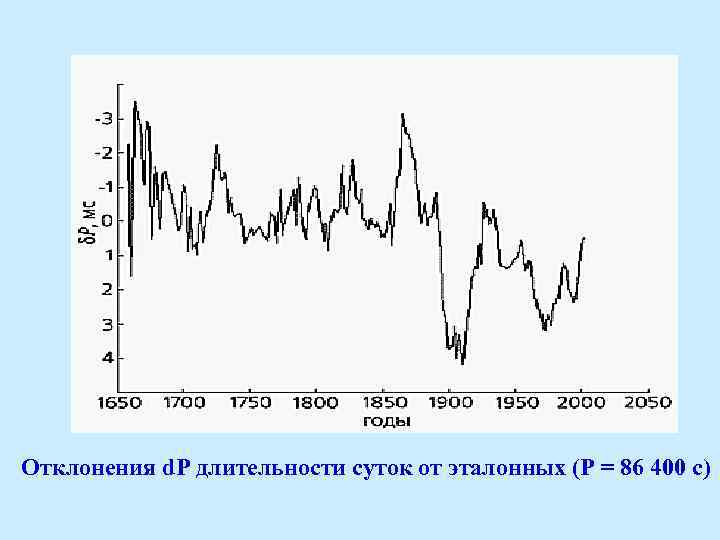Отклонения d. P длительности суток от эталонных (P = 86 400 с)

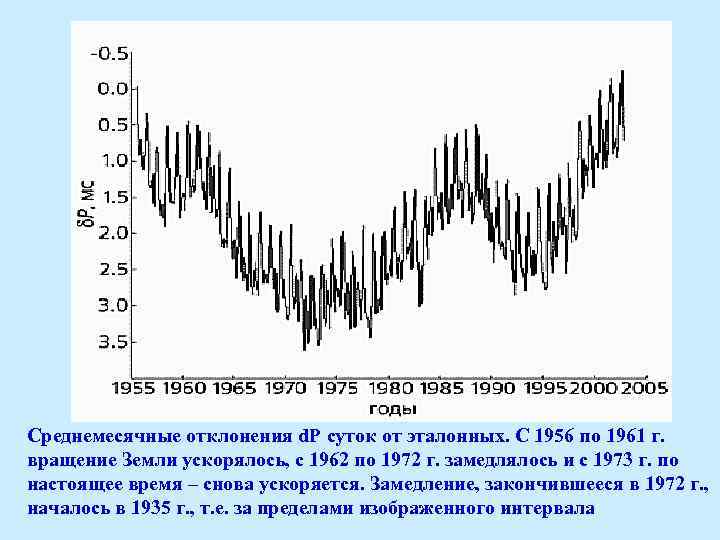Среднемесячные отклонения d. P суток от эталонных. С 1956 по 1961 г. вращение Земли ускорялось, с 1962 по 1972 г. замедлялось и с 1973 г. по настоящее время – снова ускоряется. Замедление, закончившееся в 1972 г. , началось в 1935 г. , т. е. за пределами изображенного интервала

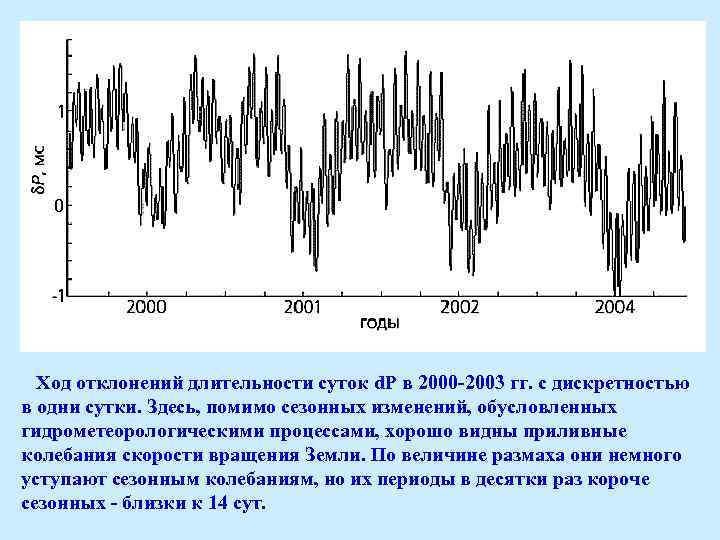Ход отклонений длительности суток d. P в 2000 -2003 гг. с дискретностью в одни сутки. Здесь, помимо сезонных изменений, обусловленных гидрометеорологическими процессами, хорошо видны приливные колебания скорости вращения Земли. По величине размаха они немного уступают сезонным колебаниям, но их периоды в десятки раз короче сезонных - близки к 14 сут.

Причина сезонной неравномерности вращения Земли – атмосферная циркуляция. В среднем атмосфера движется с запада на восток (преобладают западные ветры). Момент импульса ветров всей атмосферы составляет за год +14· 1025 кг·м 2·с– 1. Его величина меняется в течение года в полтора раза: максимум в в апреле и ноябре, минимум в августе. Момент импульса ветров всегда положителен, значит, атмосфера в целом вращается вокруг оси быстрее Земли. Суммарный момент импульсов твердой Земли и атмосферы не изменяется, что иллюстрирует справедливость закона сохранения момента импульса в глобальных масштабах. Момент импульса перераспределяется между атмосферой и твердой Землей. Когда момент импульса атмосферы увеличивается (усиливаются западные ветры), момент импульса тела Земли снижается и вращение и наоборот. Степень согласия изменений моментов импульса атмосферы и Земли в 1958 -2001 гг. иллюстрирует рис.

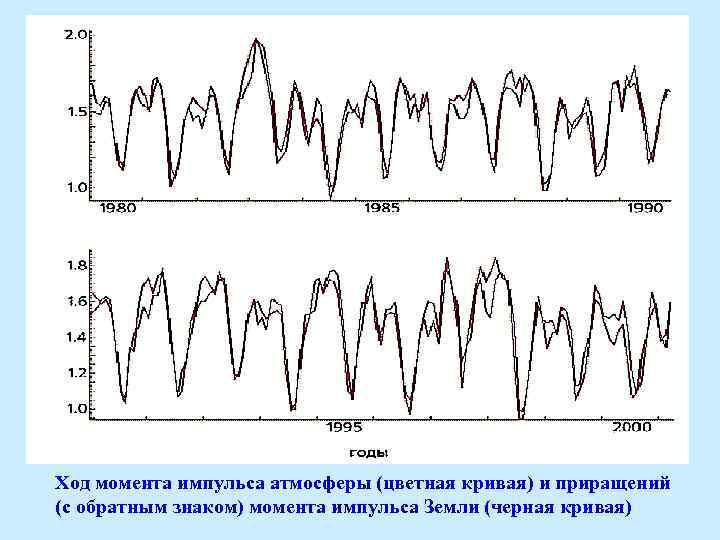Ход момента импульса атмосферы (цветная кривая) и приращений (с обратным знаком) момента импульса Земли (черная кривая)

Важна роль перераспределения воды. Около 2% воды на Земле находится в виде льда. Общая масса льда в настоящее время равна ~ 28· 1018 кг; 90% приходится на ледниковый щит Антарктиды, 9% – на ледник Гренландии и менее 1% на все остальные горные ледники. Масса ледников значительно меняется во времени. Например, 12 тыс. лет назад растаял ледниковый щит, покрывавший большие пространства Европы и Северной Америки. Около тысячи лет назад ледниковый щит Гренландии имел существенно меньшую массу, чем ныне. Перераспределение воды между Мировым океаном и ледниковыми щитами неизбежно сопровождалось изменением момента инерции Земли и должно было приводить к неравномерности ее вращения и движению полюсов.

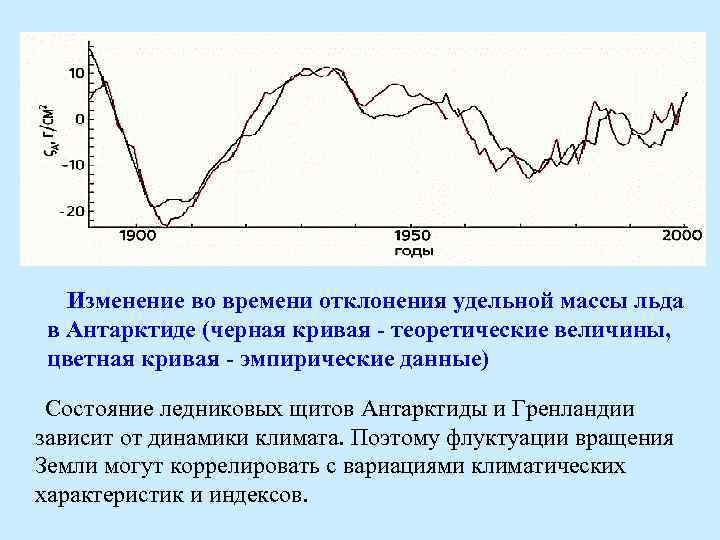Изменение во времени отклонения удельной массы льда в Антарктиде (черная кривая - теоретические величины, цветная кривая - эмпирические данные) Состояние ледниковых щитов Антарктиды и Гренландии зависит от динамики климата. Поэтому флуктуации вращения Земли могут коррелировать с вариациями климатических характеристик и индексов.

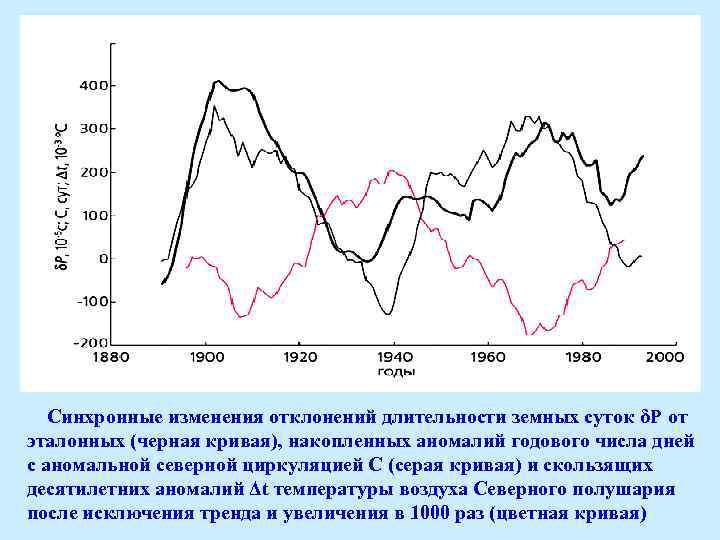Синхронные изменения отклонений длительности земных суток δP от эталонных (черная кривая), накопленных аномалий годового числа дней с аномальной северной циркуляцией С (серая кривая) и скользящих десятилетних аномалий Δt температуры воздуха Северного полушария после исключения тренда и увеличения в 1000 раз (цветная кривая)

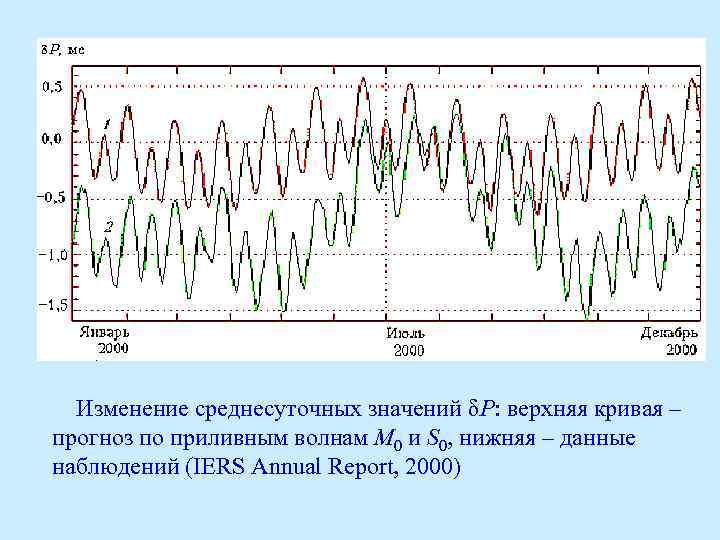Изменение среднесуточных значений δР: верхняя кривая – прогноз по приливным волнам М 0 и S 0, нижняя – данные наблюдений (IERS Annual Report, 2000)

Видно влияние полумесячного лунного и полугодового солнечного прилива – деклинационные волны с периодами 13, 66 суток солнечным периодом 182, 5 суток. Но кроме них в наблюдениях отмечаются волны с месячным и годовым периодом. Амплитуда колебаний длины суток с полугодовым периодом волны S 0 в наблюдениях больше, чем в приливной модели. Значит, действуют иные, кроме приливных, причины сезонных изменений длины суток. Это, разумеется, влияние атмосферных факторов. Главный вывод: сжатие Земли, созданное ее вращением, в свою очередь, вместе с приливным действием Луны и Солнца изменяют параметры вращения – положение оси в пространстве и в теле Земли, а также скорость вращения (длину суток). 37