Основы финансовых вычислений сложные проценты Сложные проценты

Основы финансовых вычислений сложные проценты

Сложные проценты Начисление сложных годовых процентов Присоединение начисленных процентов к сумме, которая служила базой для их начисления, называют капитализацией процентов, а способ вычисления процентных платежей по сложным процентам – вычислением "процента на процент".

Рассчитаем наращенную сумму при условии, что проценты начисляются и капитализируются один раз в год. Пусть первоначальная сумма долга равна P, в конце первого года сумма долга с присоединенными процентами составит P + Pi = P (1+i), к концу второго года: P(1+i) + P(1+i)i = P(1+i)2 и т. д. К концу n-го года первоначальная сумма достигнет величины S = P(1+i)n, где S – наращенная сумма, Р – первоначальная сумма, i – годовая ставка сложных процентов, n – срок ссуды, выраженный в годах.

Пример 1. Ссуда величиной 700 рублей выдана на 4 года при ставке сложных процентов, равной 20% годовых. Определить величину процентного платежа и сумму накопленного долга. Решение. По формуле находим: S = P(1+i)n = 700·(1+ 0, 2)4 = 1451, 52 руб. – наращенная сумма. Проценты за 4 года: I = S – P = 751, 52 руб. Для тех же данных при начислении простых процентов мы получили S = 1260 руб.

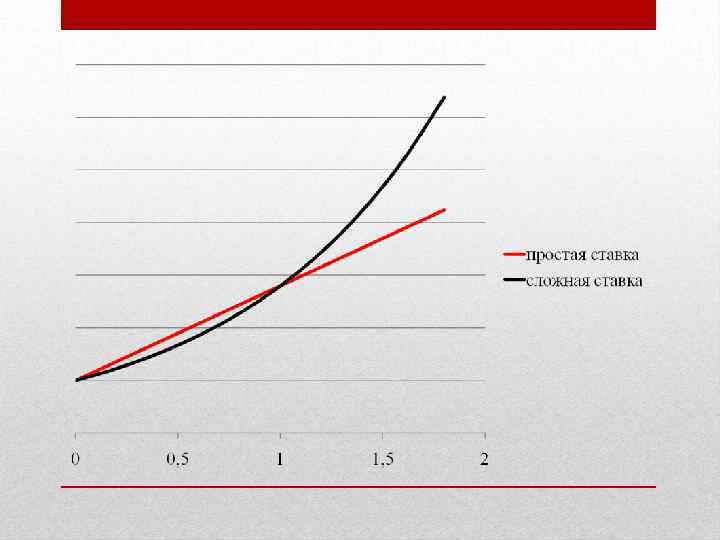
Наращение процентов m раз в году. Номинальная и эффективная ставки процентов. j – годовая ставка сложных процентов, m – число периодов начисления в году. Тогда каждый раз проценты начисляются по ставке j/m. Ставка j называется номинальной. S=P(1+ j/m)mn Чем чаще начисляются проценты, тем быстрее идет процесс наращения!

Пример 2. Ссуда величиной 700 руб. выдана на 4 года. Номинальная ставка сложных процентов – 20% годовых. Определить сумму накопленного долга, если начисление процентов производится: (1) раз в году; (2) раз в полугодие; (3) раз в квартал. Решение. (1) m = 1; j/m = 0, 2; nm = 4. S=P(1+ j/m)n=700·(1+0, 2)4=700· 2, 0736 = 1451, 52 руб. (2) m = 2; j/m = 0, 2/2 = 0, 1; nm = 4· 2 = 8. S=700·(1+0, 01)8=700· 2, 143589=1500, 51 руб. (3) m=4; j/m = 0, 2/4 = 0, 05; nm = 4· 4 = 16. S=700·(1+0, 05)16=700· 2, 182875=1528, 01 руб.

Эффективная ставка iэ – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m. (1+iэ)n=(1+ j/m)nm (iэ – эффективная, j – номинальная ставки) Связь между эффективной и номинальной ставками: При m > 1 iэ > j.

Уравнивающей (iур) называется периодическая процентная ставка, при которой капитал при mразовой капитализации начислении процентов 1 раз в год дает одинаковый результат.

Начисление процентов при дробном числе лет. Способы расчета: 1) Общий метод S=P(1+j/m)N, где N – число (возможно дробное) периодов начисления; 2) Смешанный метод S=P(1+j/m)а·(1+b·j/m), (a – целое число периодов начисления (a=[N]), b – оставшаяся дробная часть (b=N-a)); 3) Начисление только за целое число периодов начисления: S=P(1+j/m)а.

Операции со сложной учетной ставкой Математический учет. Для случаев, когда проценты начисляются m раз в году, получим:

Пример 3. Сумма в 5 тыс. руб. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов, равная 15% годовых. Решение. Дисконтный множитель для данных условий составит 1/(1+0, 15)5=0, 49718. Современная величина равна P = 5000· 0, 49718 = 2485, 88 руб. Дисконт D = 2514, 12 руб.

Банковский учет. P=S(1 – dсл)n (dсл – сложная годовая учетная ставка) Дисконт: D = S – P = S(1– dсл)n). При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением.

Пример 4. Долговое обязательство на сумму 5000 руб. , срок оплаты которого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15% годовых. Каков размер полученной за долг суммы и величина дисконта? Решение. Полученная сумма (современная величина) равна P = 5000·(1 - 0, 15)5=5000· 0, 4437=2218, 53 руб. Дисконт составил D=5000 -2218, 53=2781, 47 руб. При простой учетной ставке того же размера: P=5000·(1 - 5· 0, 15)=1250 руб. ; D= 5000 - 1250=3750 руб.

Номинальная и эффективная учетные ставки процентов. В тех случаях, когда дисконтирование применяют m раз в году, используют номинальную учетную ставку f. P=S(1 -f/m)mn Дисконтирование не один, а m раз в году быстрее снижает величину дисконта.

Пример 5. Долговое обязательство на сумму 5000 руб. , срок оплаты которого наступает через 5 лет, продано с дисконтом. Определить сумму, полученную при поквартальном учете по номинальной учетной ставке 15%. Решение. f = 0, 15; m = 4; mn = 20 Полученная за долг сумма составит P = 5000·(1 -0, 15/4)20= 5000· 0, 4656= 2328 руб. D = 2672 руб. (В примере (4) P=2218, 53 руб. ; D= 2781, 47 руб. )

Под эффективной учетной ставкой (dсл) понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m. (1 -f/m)mn=(1 -dсл)n dсл=1 -(1 -f/m)m; f=m(1 -(1 -dсл)1/m) Эффективная учетная ставка во всех случаях, когда m>1, меньше номинальной ставки (для одинаковых периодов).

Непрерывные проценты Непрерывное наращение имеет значение в анализе сложных финансовых проблем, например, при обосновании и выборе инвестиционных решений.

Наращенная сумма при дискретных процентах: S=P(1+j/m)mn. При непрерывном начислении процентов (m ) имеем:

Непрерывную ставку процентов называют силой роста и обозначают символом . S=Pe n Формула эквивалентного перехода от одних ставок к другим: (1+i)n=e n, откуда следует: =ln(1+i), i=e -1.

Дисконтирование на основе силы роста осуществляется по формуле P=Se- n. Пример 6. Определим современную стоимость платежа из примеров (4 – 5) при условии, что дисконтирование производится по силе роста 15% (S = 5000 руб. , n = 5) Решение. Современная величина равна P =5000·е-0, 15· 5= 5000· 0, 472366=2361, 83 руб. При применении дискретной сложной учетной ставки такого же размера получили величину P=2218, 53 руб.

Расчет срока ссуды и размера процентных ставок Срок ссуды. При наращении по сложной годовой ставке i: При наращении по номинальной ставке процентов j m раз в году:

При дисконтировании по сложной годовой учетной ставке d : При наращении по постоянной силе роста:

Расчет процентных ставок. При наращении по сложной годовой ставке i: При дисконтировании по сложной годовой учетной ставке d: При наращении по постоянной силе роста:

Удвоение суммы. Через сколько лет сумма ссуды возрастет в N раз при данной процентной ставке? а) начисляются простые проценты: б) начисляются сложные проценты: При N=2: