Основы финансовых вычислений Лекция 6 1 2

Основы финансовых вычислений Лекция 6 1

2. 1 Начисление сложных процентов раз в год Сущность начисления сложных процентов Сложные проценты (compound interest) - проценты, начисляемые на любые ранее выплаченные проценты и на основную сумму, взятую или отданную в долг. В основе начисления сложных процентов лежат операции: Ø капитализация процентов; Ø реинвестирование. За счет капитализации процентов база их начисления изменяется во времени. Говорят, «начисление процентов на проценты» . что происходит

Сложные проценты, как правило, начисляют в долгосрочных операциях: 1. при расчете ипотечных кредитов; 2. в долгосрочных сберегательных вкладах; 3. в операциях страхования; 4. долгосрочных инвестициях; 5. при оценке денежных потоков и т. п.

Томас Д. «Воротилы финансового мира» Джон Джейкоб Астор в 1658 г. выменял остров Манхеттен, на котором расположена центральная часть Нью-Йорка, за 24$. Стоимость земли этого острова через 350 лет оценивалась в 40 000 000 $. Для совершения такого долгосрочного инвестиционного вложения потребовалась бы простая процентная ставка в размере : rs. i. = 476 190 475, 9% а сложная всего: rc. i. = 6, 25%

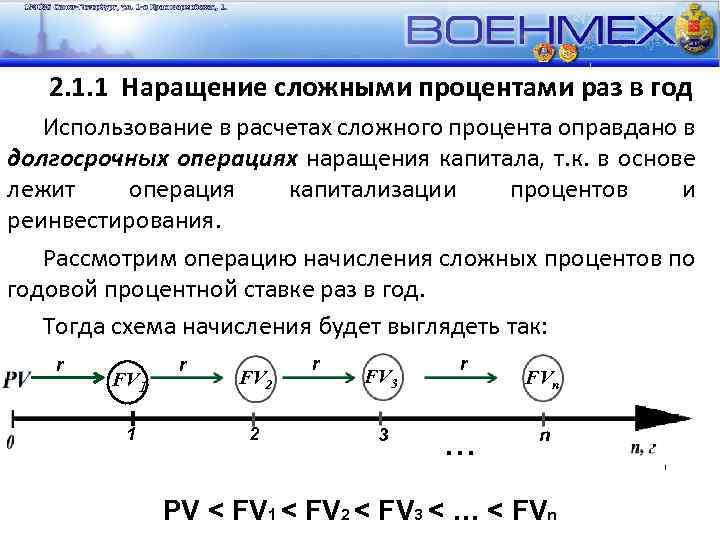2. 1. 1 Наращение сложными процентами раз в год Использование в расчетах сложного процента оправдано в долгосрочных операциях наращения капитала, т. к. в основе лежит операция капитализации процентов и реинвестирования. Рассмотрим операцию начисления сложных процентов по годовой процентной ставке раз в год. Тогда схема начисления будет выглядеть так: r FV 1 1 r FV 2 2 r FV 3 3 r … FVn n PV < FV 1 < FV 2 < FV 3 < … < FVn

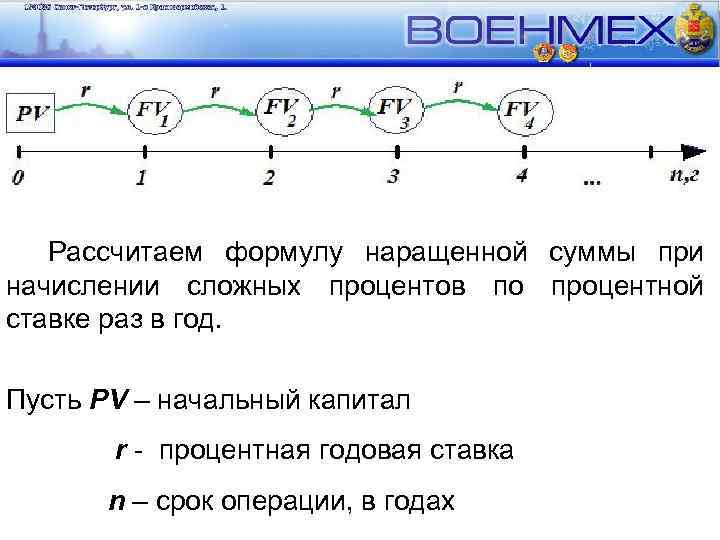Рассчитаем формулу наращенной суммы при начислении сложных процентов по процентной ставке раз в год. Пусть PV – начальный капитал r - процентная годовая ставка n – срок операции, в годах

Будем определять наращенную сумму к концу каждого года. FV 1 = PV (1+1∙r) = PV(1+r) FV 2 = FV 1 (1+1∙r) = FV 1(1+r) = PV (1+r)∙(1+r) = PV (1+r)² FV 3 = FV 2 (1+r) = PV (1+r)²(1+r) = PV (1+r)³ …. . FVn = FVn-1 (1+r) = PV (1+r)n (2. 1. 1) – начисление сложных процентов по процентной ставке раз в год

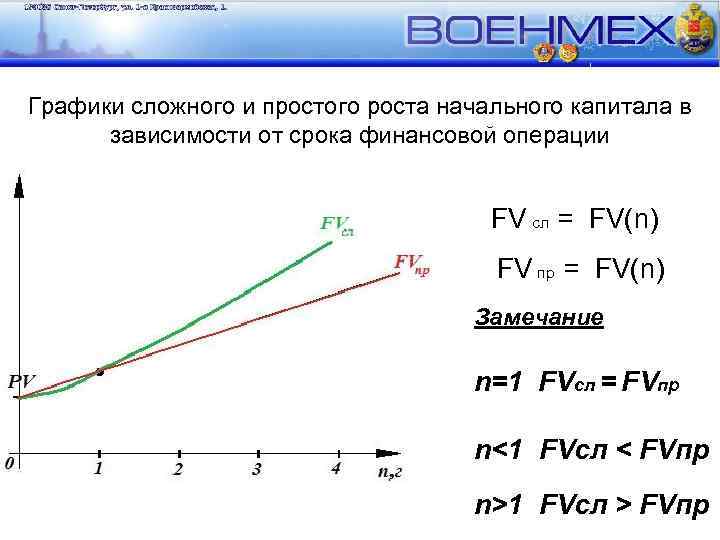Графики сложного и простого роста начального капитала в зависимости от срока финансовой операции FV сл = FV(n) FV пр = FV(n) Замечание n=1 FVсл = FVпр n<1 FVсл < FVпр n>1 FVсл > FVпр

Сумма 20 000 руб. инвестируется на 6 лет под процентную ставку 10, 00% годовых. Определите наращенную сумму при условии начисления сложных и простых процентов раз в год. Дано: PV = 20000, 00 руб. Вывод: начисление сложных проn=6 л центов в долгосрочных операциях дает r =10, 00 % больший результат, чем начисление Найти: FVпр FVсл простых процентов. Поэтому в долгосрочных операциях оправдано начисление именно сложных процентов. Уменьшим срок до полугода и сравним результаты начисления.

Сумма 20 000 руб. инвестируется на полгода под процентную ставку 10, 00% годовых. Определите наращенную сумму при условии начисления сложных и простых процентов раз в год. Дано: PV = 20000, 00 руб. n = 1/2 г. r =10, 00 % Найти: FVпр FVсл Вывод: начисление простых процентов в краткосрочной операции дает больший результат. Поэтому начисление простых процентов оправдано в краткосрочных операциях.

Основные формулы при наращении сложных процентов раз в год Сила роста капитала (2. 1. 2) - показывает во сколько раз вырос капитал за n лет или стоимость 1 у. д. ед. через n лет Величина начисленных процентов (2. 1. 3) – начисленные проценты Срок финансовой операции (2. 1. 4) – срок операции наращения

Какова величина начисленных банком процентов за 5 лет по сложной процентной ставке 10, 00% годовых и их ежегодном начислении, если вложенная сумма составила 500 000 у. ед. На какой срок необходимо вложить туже сумму, чтобы величина начисленных процентов была бы равна вложенному капиталу? Дано: PV = 500 000 у. ед. r = 10, 00% n= 5 л. Найти: I; n, если I = 500 000 у. ед. Определим величину начисленных процентов: Найдем величину срока: I = PV Если бы пришлось начислять простые проценты, то срок составил бы nпр = 10 лет

Кое-что о правилах В финансовых операциях существует много правил, позволяющих достаточно быстро и легко определять значение некоторых показателей. Например, в операциях начисления сложных процентов можно довольно быстро определить величину срока, за которое происходит удвоение первоначального капитала при наращении по процентной ставке. «Правило 72» Значение срока, при котором происходит удвоение первоначального капитала Так в предыдущем примере рассчитать значение срока, при котором происходило удвоение первоначального капитала по 10% годовой ставке, можно было по «правилу 72» : n≈72/0, 1= 7, 2 г.

2. 2 Математическое дисконтирование раз в год Математическое дисконтирование в схеме сложных процентов по своей природе ничем не отличается от дисконтирования в схеме простых процентов, т. е. также является операцией обратной к наращению процентов по процентной ставке. (2. 2. 1) – приведенная стоимость (2. 2. 2) - множитель дисконтирования (2. 2. 3) - величина дисконта

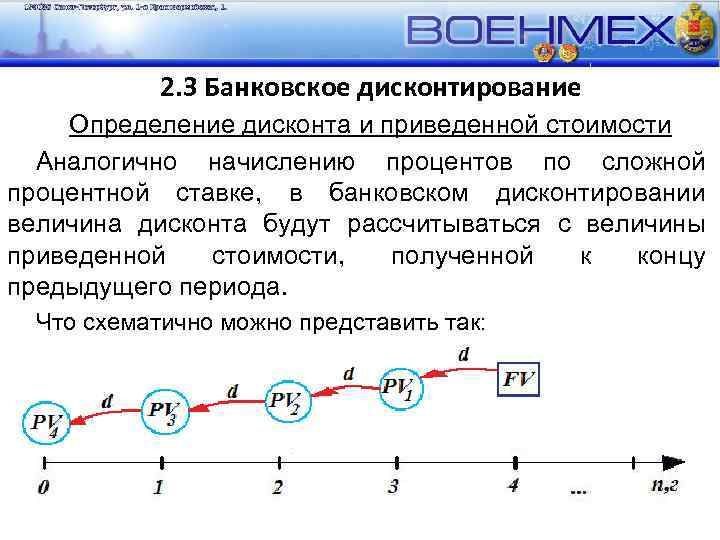2. 3 Банковское дисконтирование Определение дисконта и приведенной стоимости Аналогично начислению процентов по сложной процентной ставке, в банковском дисконтировании величина дисконта будут рассчитываться с величины приведенной стоимости, полученной к концу предыдущего периода. Что схематично можно представить так:

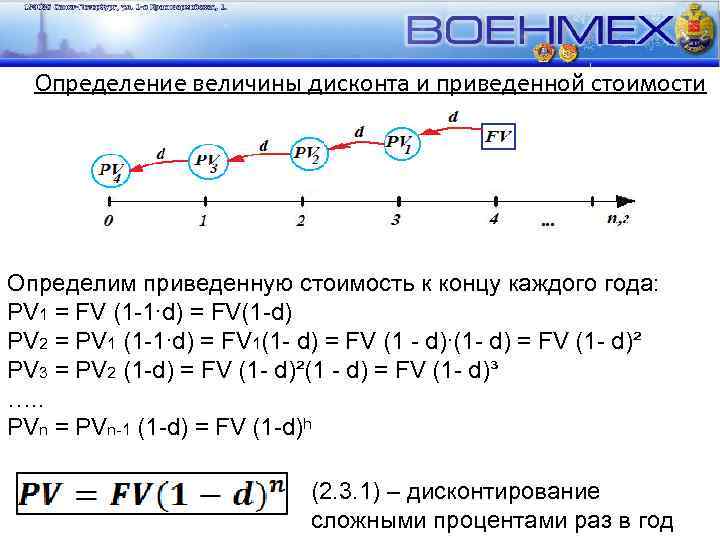Определение величины дисконта и приведенной стоимости Определим приведенную стоимость к концу каждого года: PV 1 = FV (1 -1∙d) = FV(1 -d) PV 2 = PV 1 (1 -1∙d) = FV 1(1 - d) = FV (1 - d)∙(1 - d) = FV (1 - d)² PV 3 = PV 2 (1 -d) = FV (1 - d)²(1 - d) = FV (1 - d)³ …. . PVn = PVn-1 (1 -d) = FV (1 -d)ʰ (2. 3. 1) – дисконтирование сложными процентами раз в год

2. 3 Банковское дисконтирование раз в год (2. 3. 2) – величина дисконта (2. 3. 3) - множитель дисконтирования (2. 3. 4) - срок финансовой операции

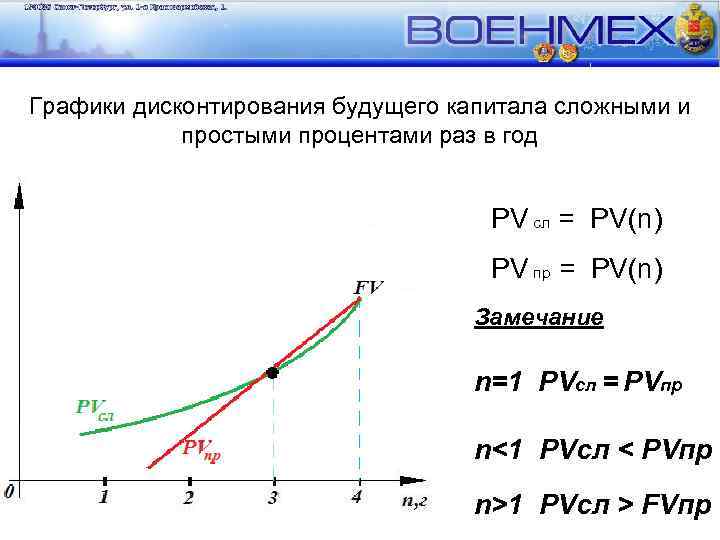Графики дисконтирования будущего капитала сложными и простыми процентами раз в год PV сл = PV(n) PV пр = PV(n) Замечание n=1 PVсл = PVпр n<1 PVсл < PVпр n>1 PVсл > FVпр

Какова приведенная стоимость векселя номиналом 670 000 руб. при его учете за 4 года до срока погашения по учетной ставке 24, 75% годовых и начислении процентов раз в год? Каков дисконт банка? Решение Дано: Так как операция долгосрочная, то FV= 670 000 руб. используются сложные проценты. d = 24, 75% n= 4 г. Найти: PV, D Дисконт банка можно определить по формуле (3. 1. 9) или вычитая дисконтированную стоимость векселя из его номинала. или

В условиях предыдущего примера рассчитать время до погашения векселя, так чтобы величина суммы, выплаченной на руки векселедержателю, была не меньше половины суммы к погашению? Дано: FV= 670 000 руб. d = 24, 75% PV ≥ 1/2 FV Найти: n

Определите номинал векселя, если при его учете за 5 лет до срока погашения его владелец получил на руки 350 455 руб. Дисконтирование осуществлялось по учетной ставке 10, 00% годовых раз в год. Т. к. операция долгосрочная, то Дано: применяют сложные проценты. PV= 350 455 руб. В соответствии с формулой дисконтирования по сложной учетной d = 10, 00% ставке, номинал векселя будет равен: n=5 л. Найти: FV

Фактически в предыдущей происходило наращение по учетной ставке. Определим процентную ставку, эквивалентную 10, 00% учетной, приносящей тот же доход за 5 лет. Для определения процентной ставки, эквивалентной учетной, нужно приравнять доход, доставленный учетной ставкой, и доход, доставленный процентной ставкой. Т. е. , тогда Ставки: d = 10% и r = 11, 11% эквивалентны

Эквивалентность ставок сложного процента В общем случае формула эквивалентности ставок при начислении сложных процентов один раз в год будет выглядеть так: (2. 3. 5, 6) – формулы эквивалентности ставок при начислении процентов раз в год

Основы финансовых вычислений Лекция 7 24

2. 4 Начисление сложных процентов m раз в год При начислении сложных процентов имеет большое значение количество начислений процентов в год. В формулах (2. 1) и (2. 3) наращения и дисконтирования можно полагать, что ставки r и d – ставки за период начисления процентов, где период равен одному году. Однако, начисление процентов может происходить чаще одного раза в год, например, раз в полугодие, раз в квартал или месяц, раз в день и чаще. Вопрос: как изменятся результаты наращения и дисконтирования, если начислять годовым ставкам чаще, чем раз в год? проценты по

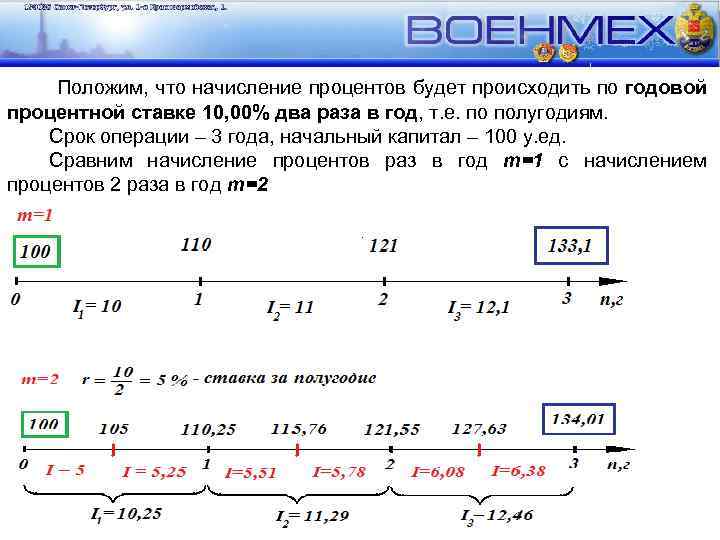Положим, что начисление процентов будет происходить по годовой процентной ставке 10, 00% два раза в год, т. е. по полугодиям. Срок операции – 3 года, начальный капитал – 100 у. ед. Сравним начисление процентов раз в год m=1 с начислением процентов 2 раза в год m=2

ВЫВЫД: чем чаще происходит начисление процентов, тем больше конечный результат наращения. Обозначим: m – количество раз начислений процентов в год. Тогда, Ø период начисления процентов будет равен 1/m лет Ø ставка наращения за период – r/m % Ø количество периодов за n лет будет равно nm. Формула наращения по годовой процентной ставке при наращении процентов m раз в год будет равна: (2. 4. 1) – наращение по годовой процентной ставке m раз в год

Определим результаты наращения по 10% годовой процентной ставке при наращении 4 и 12 раз в год, т. е. ежеквартально и ежемесячно. Сумма вложения 100 у. ед. , срок операции – 3 года Дано: PV= 100 у. ед. r = 10, 00% n= 3 г. m=4 m = 12 Найти: FV В соответствии с формулой (2. 4. 1) получим: у. ед.

Основные формулы начисления процентов m раз в год: (2. 4. 2) – доход (2. 4. 3) – сила роста капитала (2. 4. 4) – процентная ставка за период начисления процентов 1/m (2. 4. 5) – годовая процентная ставка (2. 4. 6) – срок фин. операции в годах

Определить начисленные проценты на капитал 400. 000 руб. при их начислении ежеквартально по процентной ставке 12, 00% годовых за 6 лет. Дано: PV= 400. 000 руб. r = 12, 00% n=6 л. m=4 Найти: I В соответствии с формулой (2. 4. 2) получим: Т. о. за 6 лет капитал при начислении процентов ежеквартально увеличится более, чем в 2 раза. Действительно, в соответствии с «правилом 72» срок удвоения капитала составит ≈ 72/12 = 6 лет. А так как начисление процентов происходило 4 раза в год, то величина начисленных процентов чуть больше вложенного капитала.

При этом начальный капитал увеличился Дано: в: PV= 400 тыс. руб. r = 12% n=6 л. m=4 Можно было иначе определить силу роста капитала: Найти: I

Определить величину годовой процентной ставки при начислении процентов 7 раз в год за 5 лет , чтобы вложенный капитал увеличился в 7 раз. Дано: n=5 л. m=7 В 5 = 7 Найти: r В соответствии с формулой (2. 4. 5) получим:

Определите величину процентной ставки за период, чтобы капитал 200 000 долларов за 4 года вырос втрое, если проценты начислялись ежегодно, по полугодиям, ежемесячно. Дано: PV= 200 000 $ FV= 600 000 $ n=3 г. m 1 = 1 m 2 = 2 m 3 = 12 Найти: rn В соответствии с формулой (2. 4. 4) величина ставки за год, полугодие или месяц будет равна: Замечание Величины найденных ставок эквивалентны другу

Определить срок, за который произойдет утроение начального капитала при начислении процентов ежедневно по процентной ставке 15, 00% годовых, если считать, что в году 365 дней. Дано: m = 365 Вn = 3 r= 15% Найти: n В соответствии с формулой (2. 4. 6) срок операции будет равен:

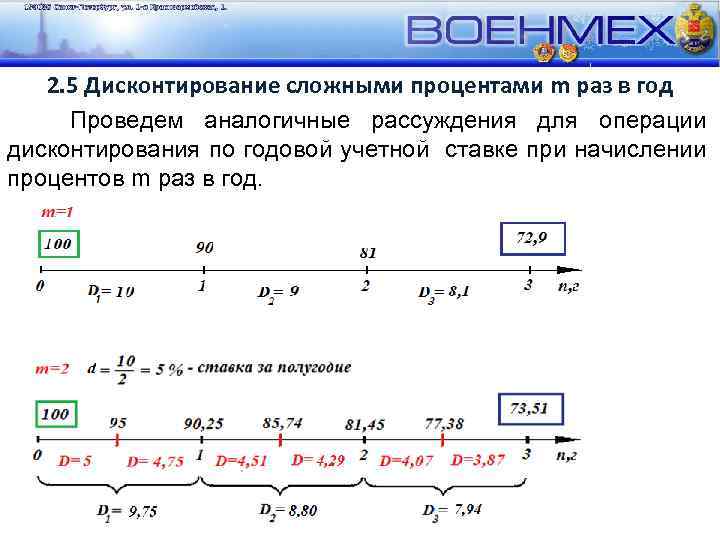2. 5 Дисконтирование сложными процентами m раз в год Проведем аналогичные рассуждения для операции дисконтирования по годовой учетной ставке при начислении процентов m раз в год.

ВЫВЫД: чем чаще происходит процентов, тем больше конечный начисление результат ДИСКОНТИРОВАНИЯ. Обозначим: m – количество раз начислений процентов в год. Тогда: Ø период начисления процентов будет равен 1/m лет Ø ставка наращения за период – d/m % Ø количество периодов за n лет будет равно nm. Формула наращения по годовой процентной ставке при наращении процентов m раз в год будет равна: (2. 5. 1) – дисконтирование по годовой процентной ставке m раз в год

Основные формулы дисконтирования при начислении процентов m раз в год: (2. 5. 2) – величина дисконта (2. 5. 3) – множитель дисконтирования (2. 5. 4) – величина учетной ставки за период начисления процентов 1/m (2. 5. 5) – срок финансовой операции