Основы дискретной математики Выполнил студент 110 гр ФМО

Основы дискретной математики Выполнил студент 110 гр. ФМО МП Богдановский Н. С.

Содержание: 1) Дискретная математика 2) Графы 3) Функции 4) Основы логики 5) Законы алгебры логики 6) Список литературы

Дискретная математика часть математики, изучающая дискретные математические структуры, такие, как графы, функции и утверждения в логике и т. д. Дискре тность(от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывность. Дискретность — всеобщее свойство материи, под дискретностью понимают: 1. Нечто, изменяющееся между несколькими различными стабильными состояниями, например механические часы, которые передвигают минутную стрелку дискретно (скачкообразно) на 1/60 часть окружности 2. Нечто, состоящее из отдельных частей, прерывистость, дробность. Например, дискретный спектр, дискретные структуры, дискретные сообщения.

ГРАФЫ Если объекты изобразить точками (вершинами), а связи линиями (ребрами), соединяющими соответствующие пары точек, то получится рисунок, называемый Графом. Теория графов находит самое широкое применение в моделировании информационных процессов, в программировании и в решении экономических задач. Она позволяет просто описывать сложные явления и дает им графическую интерпретацию. ”Картинка” графа позволяет быстро понять проблему и на интуитивном уровне разработать рациональный алгоритм решения.

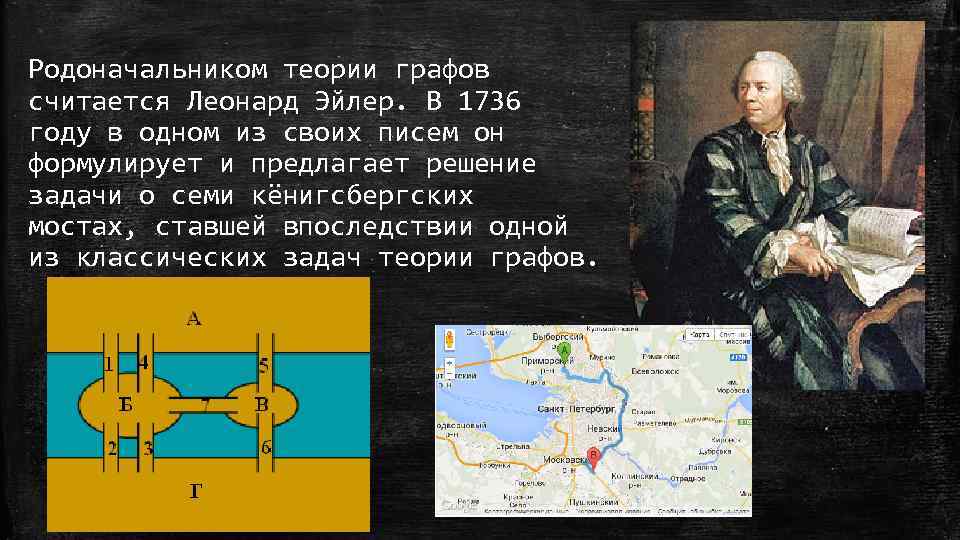Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

Задача о ходе коня — задача о нахождении маршрута шахматного коня, проходящего через все поля доски по одному разу.

X и Y – некоторые числовые множества. Если каждому элементу множества X единственным образом соответствует элемент множества Y, то это соответствие называется Функцией. Аналитический В явном виде: Функция разрешена относительно y : y = х2 В неявном виде: Функция не разрешена относительно y: F(x, y) = 0 X X 1 X 2 … Xn Графический Y Y 1 Y 2 … Yn Табличный

Классификация элементарных функций Тригонометрическая: Y=sin x, y=cos x, y=tg x, y=ctg x; Обратно тригонометрическая: Y=arcsin X, Y=arccos X, Y=arctg X, X=arcctg Y Показательная: Y=ax; Логарифмическая: Y=logax Степенная: Y=x^a; Логическая: Y = true; X = false;

Основы логики Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные в 4 веке до нашей эры древне греческими мыслителями . Первым этапом на пути в развитии логики заложил Аристотель, создав основы формальной логики, где впервые отделил логические формы речи от ее содержания. Второй этап – математическая логика, основы которой заложил в своей работе "Об искусстве комбинаторики" (1666) великий немецкий философ, математик, физик и языковед Готфрид Вильгельм Лейбниц.

Джордж Буль (1815 -1864) Основоположник математической логики считается Джордж Буль (1815 -1864), английский математик. Поэтому начальный раздел математической логики часто называют булевой алгеброй или алгеброй логики. Булевая алгебра изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству. Например {0, 1}

В современное время для анализа и синтеза схем в ЭВМ при алгоритмизации и программировании решения задач широко используется математический аппарат алгебры логики. Математическая логика Формальная система, носителем которой являются символы и последовательности символов формального языка, а множество операций используется для формирования и вывода новых суждений формального языка § Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операции над ними.

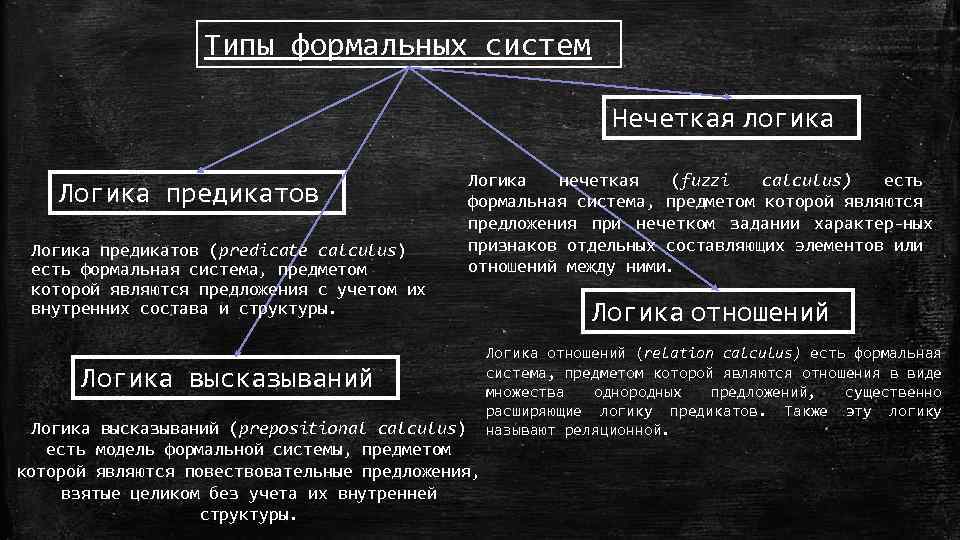Типы формальных систем Нечеткая логика Логика предикатов (predicate calculus) есть формальная система, предметом которой являются предложения с учетом их внутренних состава и структуры. Логика нечеткая (fuzzi calculus) есть формальная система, предметом которой являются предложения при нечетком задании характер ных признаков отдельных составляющих элементов или отношений между ними. Логика отношений (relation calculus) есть формальная система, предметом которой являются отношения в виде множества однородных предложений, существенно расширяющие логику предикатов. Также эту логику Логика высказываний (prepositional calculus) называют реляционной. Логика высказываний есть модель формальной системы, предметом которой являются повествовательные предложения, взятые целиком без учета их внутренней структуры.

Высказывание Любое повествовательное предложение, которое может быть признано истинным или ложным, называют высказыванием. Высказывания, которые получаются из простых предложений с помощью грамматических связок “не”, “и”, “или”, “если…, то…”, “… тогда и только тогда, когда…” и т. п. , называют сложными. Для обозначения грамматических связок в формальном языке вводят дополнительные символы, которые называют логическими связками. : =”или”, &: =“и”, : =”не”, : =“если…, то…”, : =“…тогда и только тогда, когда …”. Для построения сложных высказываний используют также вспомогательные символы “(“, “)” скобки . Модель алгебры высказываний. Множество T={A, B, C, …} с заданными над ним логическими операциями F={ ; ; } формируют модель алгебры высказываний Aв=.

Логические операции бывают унарные (или одноместные) и бинарные (или двухместные). Это определяется наличием одного или двух операндов у операции. Конъюнкция Дизъюнкция Отрицание двухместная операция, (операция НЕ)есть одноместная двухместная операция, посредством которой из двух операция, посредством которой формул F 1 и F 2 получают посредством которой из двух ее значение есть отрицание формул F 1 и F 2 получают новую формулу F=(F 1 F 2), значения операнда. ( F) новую формулу F=(F 1 F 2), описывающую сложное высказывание. Эквиваленция высказывание. Значение этого высказывания истинно тогда и только тогда, Значение этого высказывания двухместная операция, когда истинны значения двух ложно тогда и только тогда, посредством которой из двух операндов F 1 и F 2. (F 1 F 2) когда ложны значения двух формул F 1 и F 2 получают новую операндов формулу F=(F 1 F 2), описывающую сложное высказывание. F 1 или F 2. Импликация двуместная операция, посредством ко торой отражающую сложное высказывание. Значение этого высказывания ложно тогда и только тогда, когда истинно значение F 1 и ложно F 2. (F 1 F 2) Значение этого высказывания истинно тогда и только тогда, когда оба операнда F 1 и F 2 имеют одинаковые значения. (F 1 F 2)

Законы Алгебры Логики Наименование закона Равносильные формулы Fi=Fj Коммутативности (F 1 F 2)=(F 2 F 1); Ассоциативности F 1 (F 2 F 3)=(F 1 F 2) F 3; F 1 (F 2 F 3) = (F 1 F 2) F 3 Дистрибутивности F 1 (F 2 F 3)=(F 1 F 2) (F 1 F 3); F 1 (F 2 F 3)=F 1 F 2 F 1 F 3 Идемпотентности (F 1 F 2)=(F 2 F 1) F F = F; F F = F Исключенного третьего F F = и; Противоречия F F = л Де Моргана (F 1 F 2) = F 1 F 2; (F 1 F 2) = F 1 F 2. Поглощения F 1 (F 1 F 2) = F 1; ( F) = F Дополнения Свойства констант F 1 (F 1 F 2) = F 1 F л = F; F и = и; F л= л; F и = F

Список литературы: 1) Дискретная математика. Энциклопедия / Гл. ред. В. Я. Козлов. — М. : Большая российская энциклопедия, 2004 2) Андерсон Дж. Дискретная математика и комбинаторика. — М. : Вильямс, 2006 3) Яблонский С. В. Введение в дискретную математику. — М. : Наука, 1986 Спасибо за внимание