704c2d82c670f41753554b41cdf8b99e.ppt
- Количество слайдов: 26

ОСНОВЫ БИОСТАТИСТИКИ Александр Владимирович Рубанович зав. лаб. экологической генетики ИОГен РАН rubanovich@vigg. ru тел. (499) 132 -8958

Темы для обсуждения q Оценка ассоциаций «генотип-фенотип» и их значимости q Факторы, влияющие на значимость оценок q Объединение выборок и метаисследования q Учет множественности сравнений
Выявление ассоциаций «генотип-фенотип» : минимальный набор действий q q Фенотип - качественный признак Кроме этого в обоих случаях можно (например: «здоровый - больной» , «русский - татарин» ) строить различные регрессионные модели: Зависимая переменная – признак (фенотип), независимыми переменные – генотипы. Например так: A/A - 0, A/T - 1, тесту Фишера Вычисляем OR; значимость по точному T/T - 2 Фенотип - количественный признак (например: вес, содержание кальция, частота аберраций) Вычисляем средние значения признака для разных генотипов; значимость по критерию Манна-Уитни
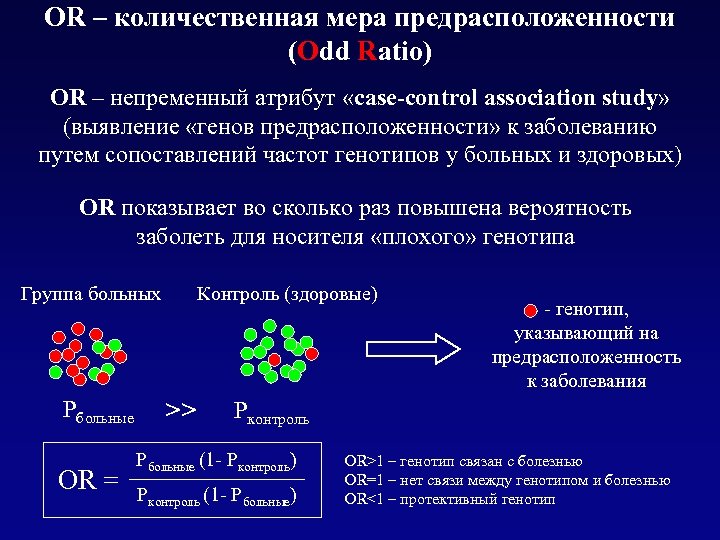
OR – количественная мера предрасположенности (Odd Ratio) OR – непременный атрибут «case-control association study» (выявление «генов предрасположенности» к заболеванию путем сопоставлений частот генотипов у больных и здоровых) OR показывает во сколько раз повышена вероятность заболеть для носителя «плохого» генотипа Группа больных >> Рбольные OR = Контроль (здоровые) Р - генотип, указывающий на предрасположенность к заболевания Рконтроль (1 - Р ) больные контроль ___________ Рконтроль (1 - Рбольные) OR>1 – генотип связан с болезнью OR=1 – нет связи между генотипом и болезнью OR<1 – протективный генотип
Soft для вычисления OR и проведения матаисследований Win. Pepi Portal (2010) - computer programs for epidemiologists q q Free! 30 дней
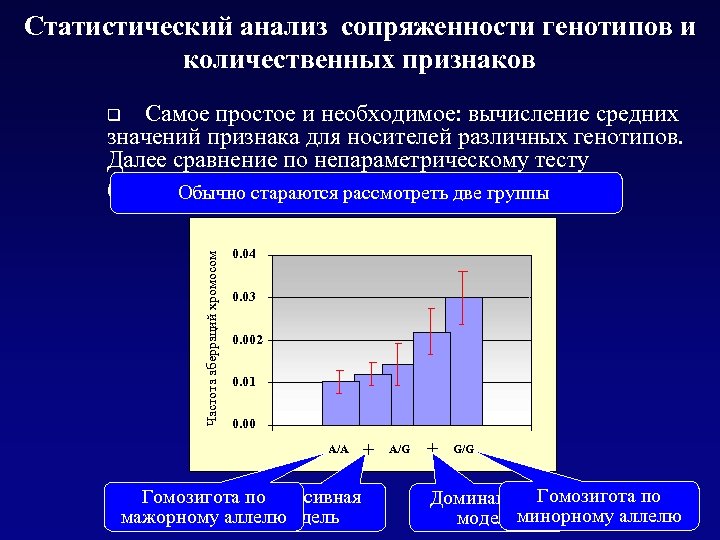
Статистический анализ сопряженности генотипов и количественных признаков Самое простое и необходимое: вычисление средних значений признака для носителей различных генотипов. Далее сравнение по непараметрическому тесту (не по Стьюденту!) Обычно стараются рассмотреть две группы Частота аберраций хромосом q 0. 04 0. 03 0. 002 0. 01 0. 00 A/A Гомозигота по Рецессивная мажорному аллелю модель + A/G + G/G Гомозигота по Доминантная модельминорному аллелю

Статистический анализ сопряженности генотипов и количественных признаков Самое простое и необходимое: вычисление средних значений признака для носителей различных генотипов. Далее вычисляется OR Далее сравнение по непараметрическому тесту и значимость по точному критерию Фишера. В данном (не по Стьюденту!) примере риск возникновения q аберраций у носителей минорного аллеля G равен OR=2, 1 и р=0, 015 Сравнение частот генотипов для групп с низким (или высоким) значением признака q 40 30 20 10 0 G/G 50 Частота, % , Частота, % 60 Группа людей с нулевым уровнем аберраций 50 40 G/G A/G 30 20 A/G A/A 10 0 -1 1 -2 2 -3 3 -4 4 -5 5 -6 Частота аберраций на 100 клеток >6 0 0 1 Частота аберраций на 100 клеток
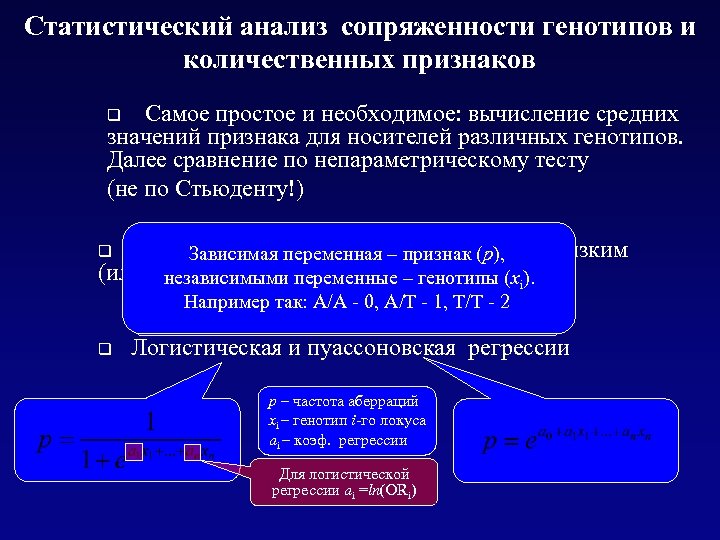
Статистический анализ сопряженности генотипов и количественных признаков Самое простое и необходимое: вычисление средних значений признака для носителей различных генотипов. Далее сравнение по непараметрическому тесту (не по Стьюденту!) q Сравнение частот генотипов для групп с низким Зависимая переменная – признак (р), (или высоким) значением признака независимыми переменные – генотипы (xi). q Нелинейные многомерные регрессии, Например так: A/A - 0, A/T - 1, T/T - 2 реализованные в пакетах Statistica и SPSS q Логистическая и пуассоновская регрессии р – частота аберраций xi – генотип i-го локуса аi – коэф. регрессии Для логиcтической регрессии ai =ln(ORi)
Soft для работы с генотипами и гаплотипами q Win. Stat for Excel Free! q X. Sole, E. Guino, J. Valls, R. Iniesta 1, V. Moreno (2006) http: //bioinfo. iconcologia. net/index. php? module=Snpstats q http: //www. bios. unc. edu/~lin/hapstat/ Free!

Темы для обсуждения q Оценка ассоциаций «генотип-фенотип» и их значимости q Факторы, влияющие на значимость оценок q Объединение выборок и метаисследования q Учет множественности сравнений

Чуть-чуть об ошибках статистических тестов Нулевая. Традиционно биологпредположение об отсутствии гипотеза – обычно ориентирован на контроль ошибки I рода одной генеральной совокупности различий = 2 выборки из(через уровень значимости), т. е. на гарантии отсутствия ложных открытий, Ошибка I рода ( ) Вероятность отвергнуть правильную нулевую гипотезу = Вероятность обнаружить различия там, где их нет = Вероятность совершить фальшивое открытие Ошибка II рода ( ) Вероятность принять неправильную нулевую гипотезу = Вероятность не обнаружить существующие различия = Вероятность упустить открытие Мощность теста = 1 - Ошибка II рода о возможности … и при этом мало заботится = Вероятность правильно отвергнуть нулевую гипотезу упустить открытие (ошибка II рода) Вероятность не упустить открытие

От чего зависят ошибки статистических тестов? q От размаха реально существующих отличий и разброса данных q От объемов выборок Ошибка I рода (вероятность фальшивого открытия) С увеличением объема выборки мощность теста слабо зависит от объемов выборок, (вероятность не упустить открытие) q Ошибки I и II рода однозначно не связаны. В целом если они сравнимы по величине всегда возрастает ошибка II рода растет при уменьшении ошибки I рода Крайний случай: «критерий» св. Фомы Неверующего (0033) Ошибка I рода = 0 Ошибка II рода = 1
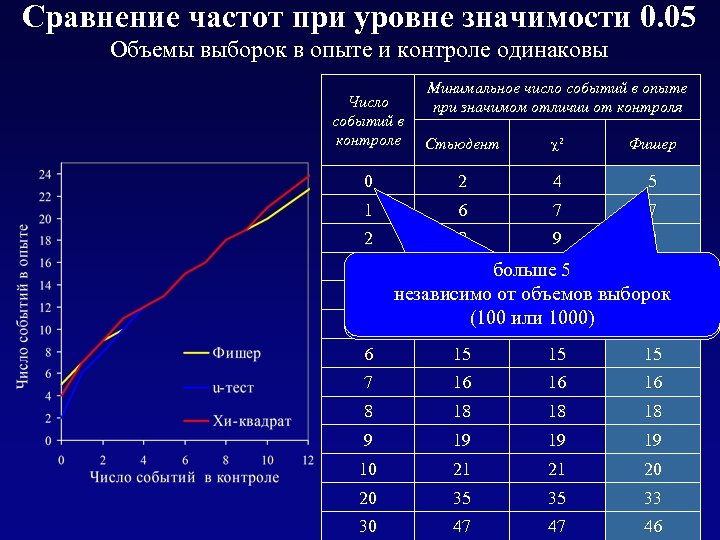
Сравнение частот при уровне значимости 0. 05 Объемы выборок в опыте и контроле одинаковы Минимальное число событий в опыте при значимом отличии от контроля Число событий в контроле Стьюдент 2 Фишер 0 2 4 5 1 6 7 7 2 8 9 9 3 10 11 10 6 15 15 15 7 16 16 16 8 18 18 18 9 19 10 21 21 20 20 35 35 33 30 47 47 46 больше 5 Если в контроле нет мутаций, то при 4 независимо от объемов выборок 12 12 значимости отличий в 12 опыте их должно или 1000) 5 13(100 быть 13 13

Темы для обсуждения q Оценка ассоциаций «генотип-фенотип» и их значимости q Факторы, влияющие на значимость оценок q Объединение выборок и метаисследования q Учет множественности сравнений

Проверка однородности материала и вычисление OR для нескольких выборок q Индекс рассеяния для биномиальных выборок Можно ли объединить k независимых выборок и оценить частоту как Объем выборки Число мутаций Частота N 1 n 1 p 1 N 2 n 2 p 2 …. …. Nk nk pk q Mantel-Haenszel test Выборки можно объединять, если
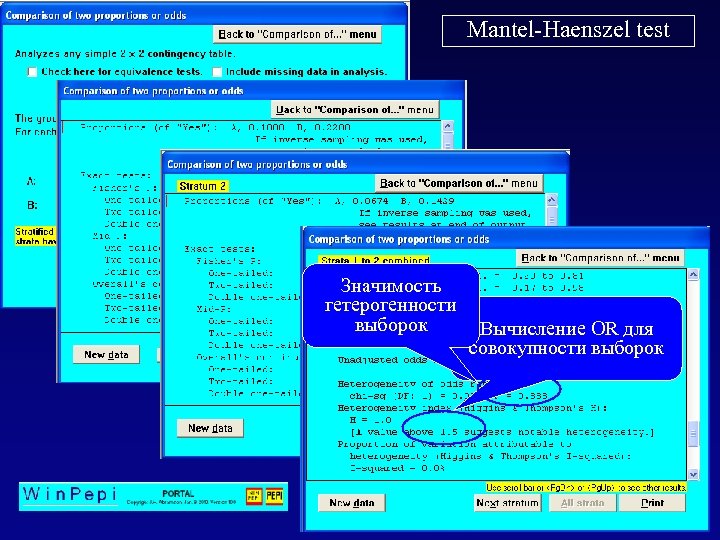
Mantel-Haenszel test Значимость гетерогенности выборок Вычисление OR для совокупности выборок
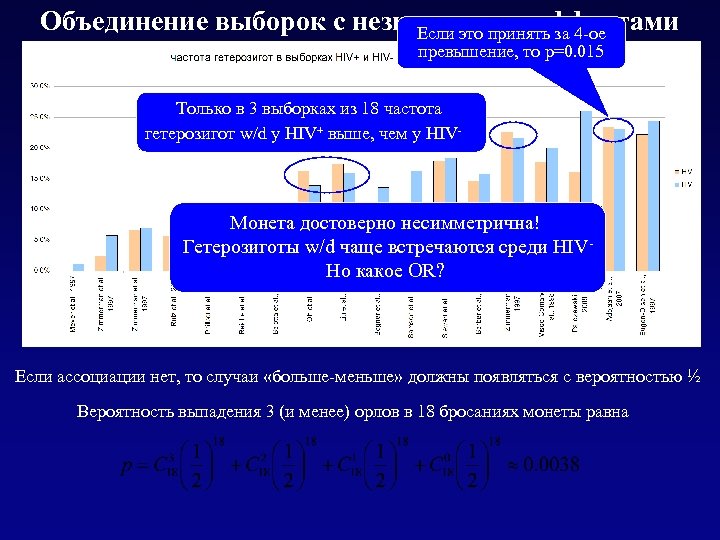
Объединение выборок с незначимыми эффектами Если это принять за 4 -ое превышение, то р=0. 015 Только в 3 выборках из 18 частота гетерозигот w/d у HIV+ выше, чем у HIV- Монета достоверно несимметрична! Гетерозиготы w/d чаще встречаются среди HIVНо какое OR? Если ассоциации нет, то случаи «больше-меньше» должны появляться с вероятностью ½ Вероятность выпадения 3 (и менее) орлов в 18 бросаниях монеты равна
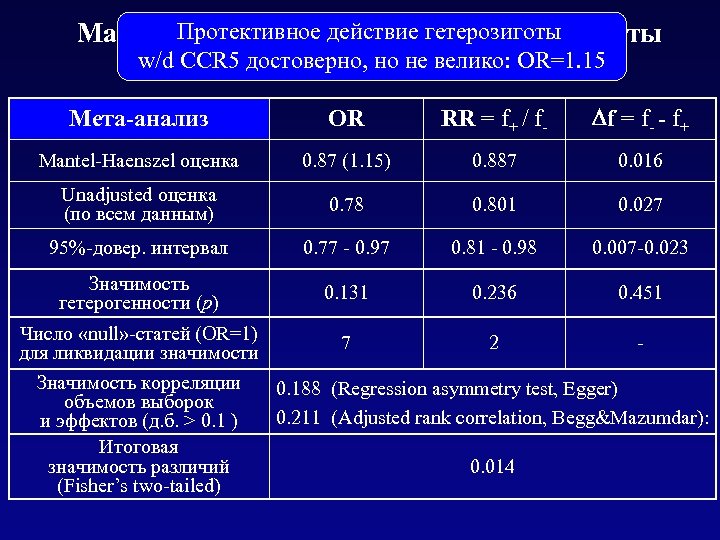
Протективное with Win. Pepi: результаты Mantel-Haenszel testдействие гетерозиготы w/d CCR 5 достоверно, но не велико: OR=1. 15 Мета-анализ OR RR = f+ / f- f = f- - f+ Mantel-Haenszel оценка 0. 87 (1. 15) 0. 887 0. 016 Unadjusted оценка (по всем данным) 0. 78 0. 801 0. 027 95%-довер. интервал 0. 77 - 0. 97 0. 81 - 0. 98 0. 007 -0. 023 Значимость гетерогенности (р) 0. 131 0. 236 0. 451 Число «null» -статей (OR=1) 7 2 для ликвидации значимости Значимость корреляции 0. 188 (Regression asymmetry test, Egger) объемов выборок 0. 211 (Adjusted rank correlation, Begg&Mazumdar): и эффектов (д. б. > 0. 1 ) Итоговая 0. 014 значимость различий (Fisher’s two-tailed)

Темы для обсуждения q Оценка ассоциаций «генотип-фенотип» и их значимости q Факторы, влияющие на значимость оценок q Объединение выборок и метаисследования q Учет множественности сравнений
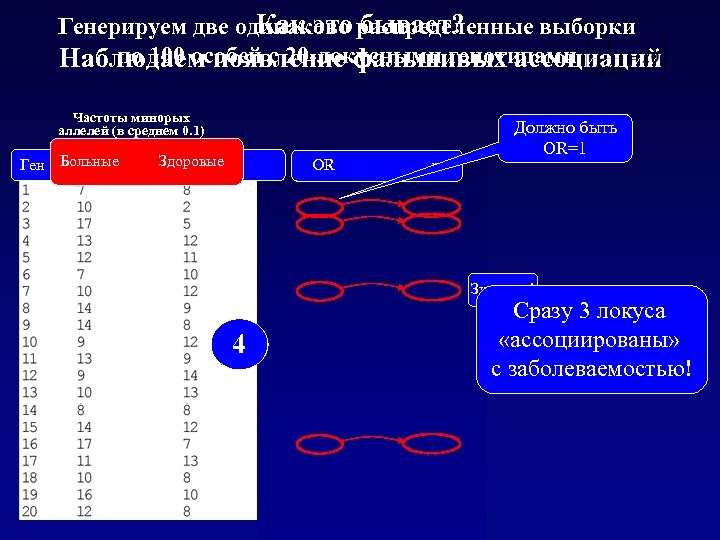
Как это бывает? Генерируем две одинаково распределенные выборки по 100 особей с 20 -локусными генотипами Наблюдаем появление фальшивых ассоциаций Частоты минорых аллелей (в среднем 0. 1) Ген Больные 1 Выборка Здоровые Выборка 2 OR p Должно быть OR=1 Значимо! 4 2 3 1 Сразу 3 локуса «ассоциированы» с заболеваемостью!

Как избежать фальшивых открытий? q Правило Карло Бонферрони (1935): При проведение m независимых статистических тестов значимы только те результаты, для которых q False Discovery Rate control: FDR - контроль q Permutation test (компьютерная перестановка лэйблов «case-control» )
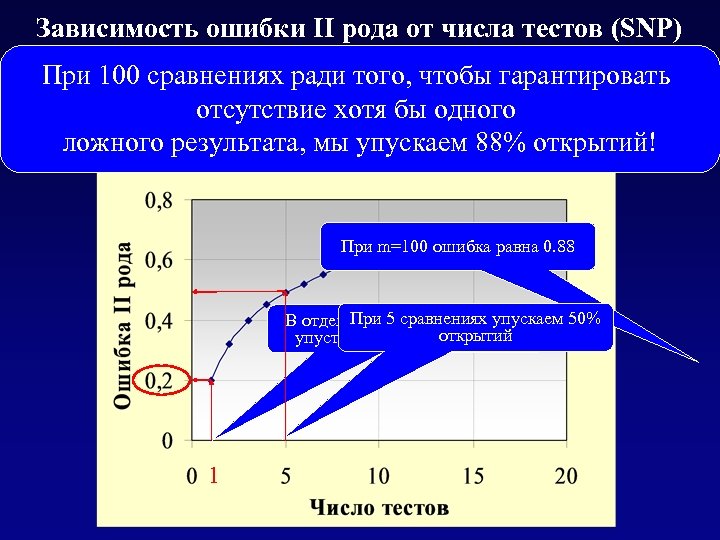
Зависимость ошибки II рода от числа тестов (SNP) при использовании поправки Бонферрони При 100 сравнениях ради того, чтобы гарантировать Вероятность пропустить ген с OR=2. 7 отсутствие хотя бы одного на выборках 100 (case) и 100 (control) ложного результата, мы упускаем 88% открытий! При m=100 ошибка равна 0. 88 При тесте вероятность В отдельном 5 сравнениях упускаем 50% упустить открытиеоткрытий равна 0. 2 1
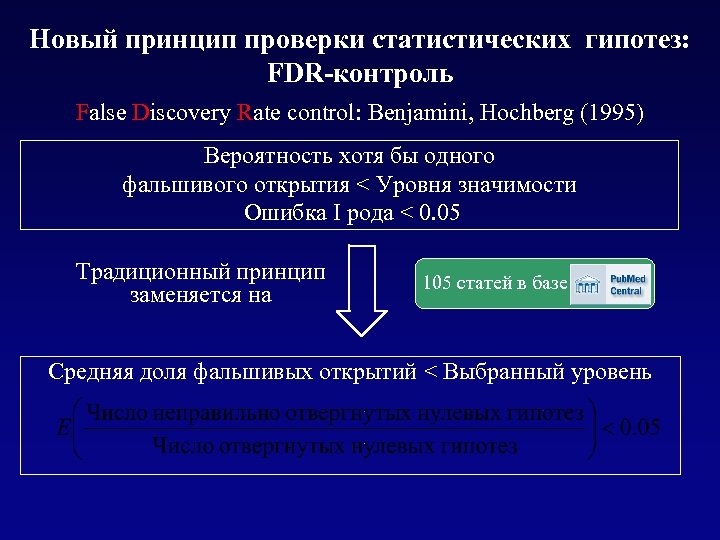
Новый принцип проверки статистических гипотез: FDR-контроль False Discovery Rate control: Benjamini, Hochberg (1995) Вероятность хотя бы одного фальшивого открытия < Уровня значимости Ошибка I рода < 0. 05 Традиционный принцип заменяется на 105 статей в базе Средняя доля фальшивых открытий < Выбранный уровень
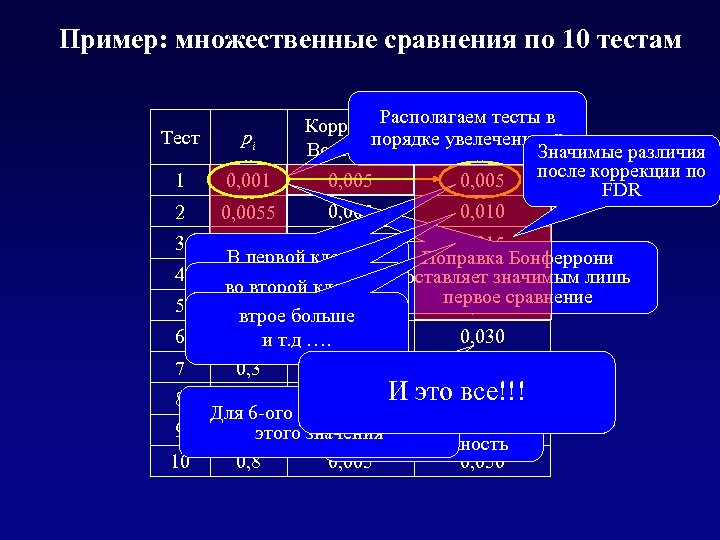
Пример: множественные сравнения по 10 тестам Располагаем тесты Коррекция по в порядке увелечения p Bonferroni FDR Значимые различия после коррекции по 0, 005 FDR Тест pi 1 0, 001 2 0, 0055 3 0, 005 0, 01 В первой клетке 0, 005 0, 015 как второй клетке во у Бонферрони, 0, 005 0, 02 больше, вдвое больше втрое 0, 04 т. д …. 0, 005 и 0, 005 0, 3 4 5 6 7 8 9 10 0, 005 0, 010 0, 015 Поправка Бонферрони 0, 020 оставляет значимым лишь первое сравнение 0, 025 0, 030 0, 035 все!!! 0, 005 И это 0, 040 без 0, 5 Значимые различия Для 6 -ого теста p больше на 0, 005 0, 6 этого значенияпоправок 0, 045 множественность 0, 005 0, 050 0, 8

Что делать, если FDR не помогает? Permutation tests: случайные перестановки пометок «case-control» в компьютерных симуляциях по алгоритму: q В исходной базе данных делаем случайную перестановку лейблов case-control q Тем самым мы уровни для каждого гена (pperm Вычисляем заново p-отказываемся от попыток ) q Вычисляем откорректированное p как Точный тест Фишера – это тоже permutation test, вычислить значимость различий. только реализованный. N раз (минимум 10000), фиксируя аналитически (р вычисляется q Повторяем процедуру Вместо этого мы ее «измеряем» экспериментально, по случаи, когда p формулам комбинаторной теории вероятностей) разыгрывая ситуацию на компьютереp perm меньше исходного значения
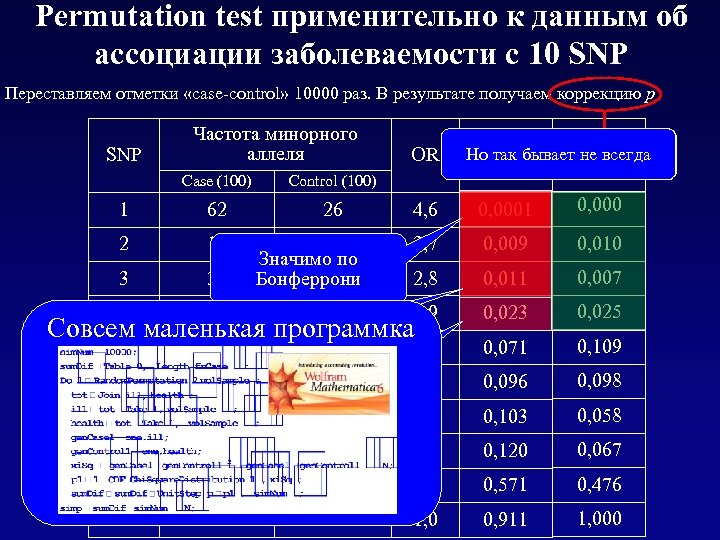
Permutation test применительно к данным об ассоциации заболеваемости с 10 SNP Переставляем отметки «case-control» 10000 раз. В результате получаем коррекцию p SNP Частота минорного аллеля Case (100) 62 26 2 19 3 31 4 20 5 Но так бывает не всегда p` p Indulgentia Control (100) 1 OR 4, 6 0, 0001 0, 000 3, 7 0, 009 0, 010 2, 8 0, 011 0, 007 2, 9 0, 023 0, 025 3, 0 0, 071 0, 109 2, 0 0, 096 0, 098 7 11 Значимо побез Значимо 4 FDR коррекции на 23 множественность 13 44 30 1, 8 0, 103 0, 058 8 54 39 1, 8 0, 120 0, 067 9 59 53 1, 3 0, 571 0, 476 10 40 41 1, 0 0, 911 1, 000 6 Значимо по 14 Бонферрони 8 Совсем маленькая программка 6
704c2d82c670f41753554b41cdf8b99e.ppt