Основы алгоритмизации Тема 14

Основы алгоритмизации Тема 14

Алгоритмы и величины Этапы решения задачи на ЭВМ (технологическая цепочка решения задачи на ЭВМ) 1. Постановка задачи (что дано и что найти) 2. Формализация задачи (математическая модель) 3. Построение алгоритма (псевдокоды, блок-схемы) 4. Составление программы на языке программирования 5. Отладка и тестирование программы 6. Проведение расчетов и анализ полученных результатов Первые 3 этапа – без ПК. Знания и навыки программиста: • Уметь строить алгоритмы • Знать языки программирования • Уметь работать в соответствующей системе

Алгоритмы и величины Понятие алгоритма Алгоритм – Algorithmi – Мухаммед аль-Хорезми (787 - 850) Алгоритм – последовательность действий, которую надо выполнить для решения некоторой задачи Алгоритм – последовательность команд управления каким-либо исполнителем Алгоритм – строго детерминированная последователь- ность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд. Алгоритм – понятное и точное предписание исполни-телю выполнить конечную последовательность команд, приводящую от исходных данных к искомому результату

Алгоритмы и величины Понятия, связанные с понятием алгоритма Исполнитель алгоритма – тот объект или субъект, для управления которым составлен алгоритм Система команд исполнителя – вся совокупность команд, которые исполнитель умеет выполнять Среда исполнителя – это обстановка, в которой функционирует исполнитель Полный набор данных – это необходимый и достаточ- ный набор данных для решения поставленной задачи Алгоритм – это точная конечная система предписаний, определяющая содержание и порядок действий исполни- теля над некоторыми объектами (исходными и промежу- точными данными) для получения (после конечного числа шагов) искомого результата

Алгоритмы и величины Свойства алгоритма • Дискретность (любой А. состоит из шагов) • Детерминированность (шаги А. выполняются Испол- нителем в строго определенной последовательности) • Понятность (А. содержит команды на понятном Исполнителю языке) • Результативность (А. обеспечивает получение результата при любых исходных данных) • Конечность (А. всегда заканчивается за конечное число шагов) • Массовость (любой А. применим к большому количеству однотипных объектов)

Алгоритмы и величины Замечания: • Алгоритм всегда рассчитан на выполнение «неразмышляющим» исполнителем • Иногда существуют способы решения задачи, не являющиеся алгоритмами • Существуют задачи, вообще не имеющие алгоритма решения • Если существует алгоритм решения задачи, то он не единственный • Не бывает одного «наилучшего» алгоритма решения задачи • Способы записи (описания) алгоритма: • вербально (текстовая форма записи) • графически (блок-схема) • в псевдокодах (на алгоязыке) • На ЯПВУ (программный код) • Любой А. состоит из трех базовых алгоритмических

Алгоритмы и величины Алгоритмы работы с величинами В разделе информатики под названием «Программиро- вание» изучаются методы программного управления работой ЭВМ. Т. е. исполнителем А. является компьютер. Компьютер работает с величинами – различными инфор-мационными объектами, имеющими имя, значение и тип. Алгоритмы, предназначенные для управления компь- ютером, называют алгоритмами работы с величинами Исполнитель А. работы с величинами (компьютер или человек) должен обладать памятью для хранения величин

Алгоритмы и величины Алгоритмы работы с величинами Программа – алгоритм, записанный на «понятном» для компьютера языке. По отношению к программе данные делятся на исход- ные, промежуточные и окончательные (результаты) Программа Исходные данные (промежуточные Результаты данные)

Алгоритмы и величины Величина имя значение тип Величины: постоянные(константы) и переменные Постоянная величина – не изменяет своего значения в ходе выполнения. Может обозначаться собственным значением или символическим именем. Переменная величина – может изменять свое значение в ходе выполнения алгоритма. Всегда обозначается символическим именем. Всякая величина занимает свое определенное место

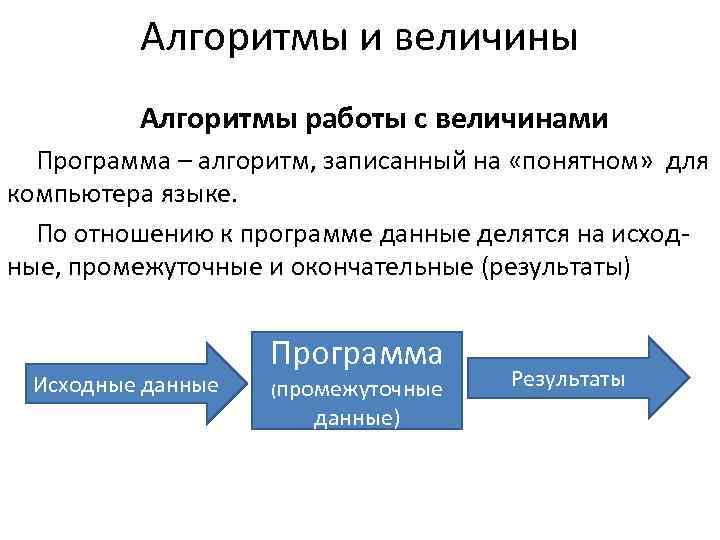
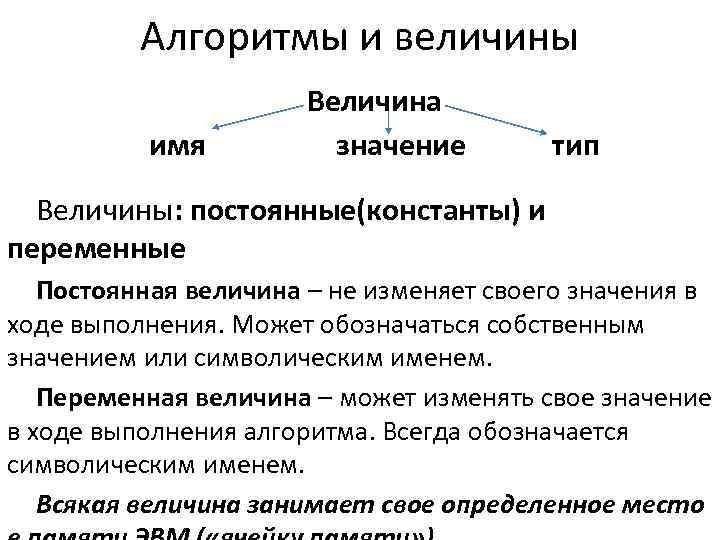
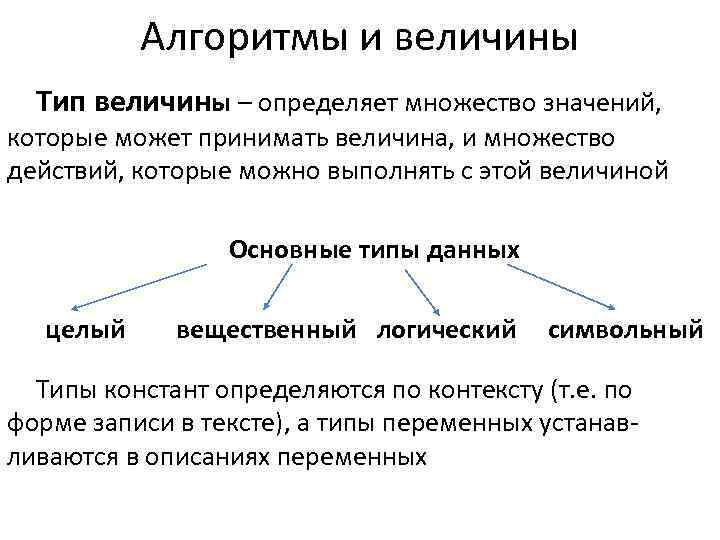
Алгоритмы и величины Тип величины – определяет множество значений, которые может принимать величина, и множество действий, которые можно выполнять с этой величиной Основные типы данных целый вещественный логический символьный Типы констант определяются по контексту (т. е. по форме записи в тексте), а типы переменных устанав- ливаются в описаниях переменных

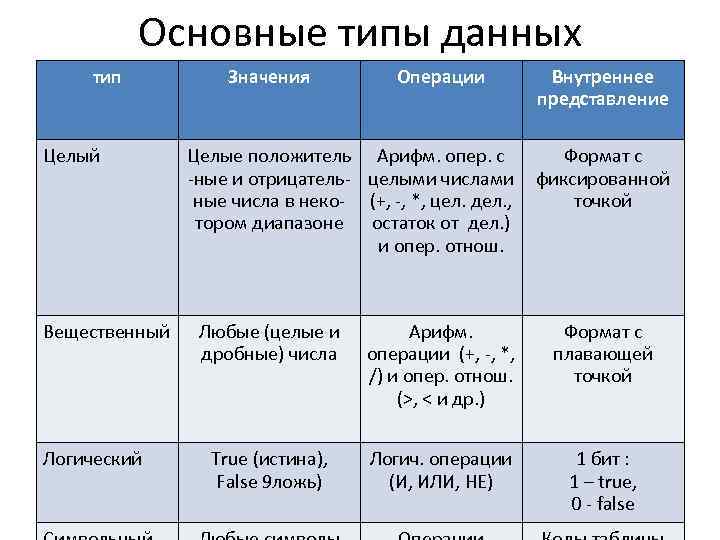
Основные типы данных тип Значения Операции Внутреннее представление Целый Целые положитель Арифм. опер. с Формат с -ные и отрицатель- целыми числами фиксированной ные числа в неко- (+, -, *, цел. дел. , точкой тором диапазоне остаток от дел. ) и опер. отнош. Вещественный Любые (целые и Арифм. Формат с дробные) числа операции (+, -, *, плавающей /) и опер. отнош. точкой (>, < и др. ) Логический True (истина), Логич. операции 1 бит : False 9 ложь) (И, ИЛИ, НЕ) 1 – true, 0 - false

ЭВМ – исполнитель алгоритмов Любой алгоритм составляется для конкретного исполнителя. Программирование – исполнитель компьютер (ЭВМ + система программирования = Виртуальная ЭВМ) Система программирования Программа на ЯПВУ ЭВМ

Алгоритмы и величины Алгоритм решения любой задачи на ЭВМ может быть составлен из команд (независимо от того, на каком языке программирования он написан) • Присваивания • Ввода • Вывода • Обращения к вспомогательному алгоритму • Цикла • Ветвления

Алгоритмы и величины Выражение – запись, определяющая последователь- ность действий над величинами. Выражение может содержать константы, перемен- ные, знаки операций, функции. Команда присваивания – команда исполнителя, в результате которой переменная получает новое значение. Формат команды: <имя переменной> : = <выражение> Порядок исполнения команды присваивания: 1. Вычисление значения <выражения> 2. Присваивание полученного значения переменной

Алгоритмы и величины Пример 1: Переменная А имела значение 6. Какое значение получит переменная А после выполнения команды А : = 2*А – 1. Пример 2: Написать последовательность команд присваивания, в результате выполнения которых переменные А и В поменяются местами. Замечание : для проверки работоспособности алгоритма строится трассировочная таблица (пусть А=3, В=7) № команда А В С 1 3 7 2 С: =А 3 7 3 А: =В 7 7 3 4 В: =С 7 3 3

Алгоритмы и величины Пример 3: Алгоритм «Волшебник» . Имеются песочные часы на 3 минуты и 8 минут. Для приготовления эликсира бессмертия его надо варить ровно 7 минут. Составить алгоритм приготовления Замечание: составьте алгоритм для приготовления эликсира за 1, 2, 4, 5, 9, 10 минут. Пример 4. Алгоритм «Перевозчик» . Перевезти на другой берег волка, козу и капусту. Пример 5. Алгоритм поиска корней квадратного уравнения. Составить трассировочную таблицу для проверки алгоритма на примере х2 – 6 х + 8 = 0 http: //infolike. narod. ru/algoritm 9. htm ЕГЭ А 18 - робот

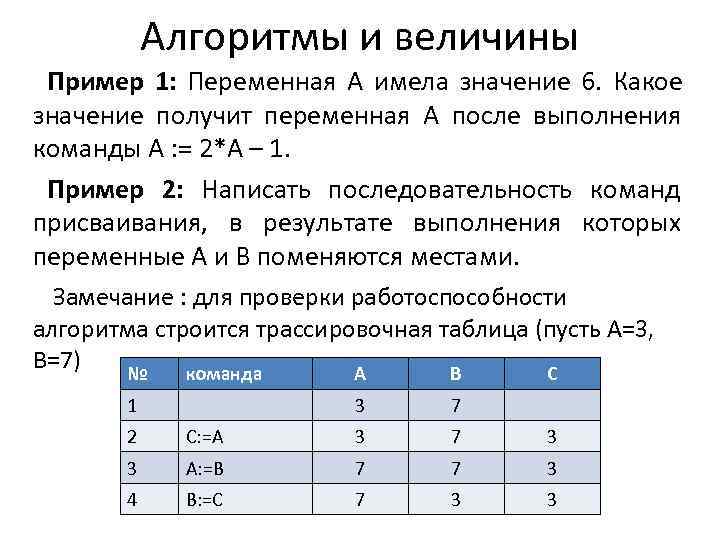
Алгоритмы и величины Домашнее задание: Задача 1: Написать алгоритм вычисления по формуле: y = (1 – x 2 + 2, 5 x 3 + x 4)2, учитывая следующие ограничения: 1) пользоваться можно только операциями сложения, вычитания и умножения; 2) каждое выражение может содержать только одну арифметическую операцию. Задача 2: Пользуясь теми же ограничениями, написать наиболее короткие алгоритмы вычисления: у = х15. Выполнить трассировку для х = 2. Задача 3: Записать алгоритм циклического перемещения влево значений между переменными А, В, С: А←В←С

Блок-схемы алгоритмов Основные алгоритмические конструкции Тема 15

Блок-схемы алгоритмов Алгоритм решения любой задачи составляется из команд Присваивания, Ввода, Вывода, Обращения к вспомогательному алгоритму, Цикла, Ветвления. • Команда присваивания – присваивает новое значение переменной, стоящей слева от знака присваивания • Команда ввода – команда, по которой значения переменных задаются через устройства (например, клавиатуру) • Команда вывода – команда, по которой значение величины отражается на устройстве вывода компьютера (на мониторе) • Команда ветвления – разделяет алгоритм на два пути в зависимости от некоторого условия, затем исполнение алгоритма выходит на общее продолжение • Команда цикла – обеспечивает повторное выполнение последовательности команд по некоторому условию

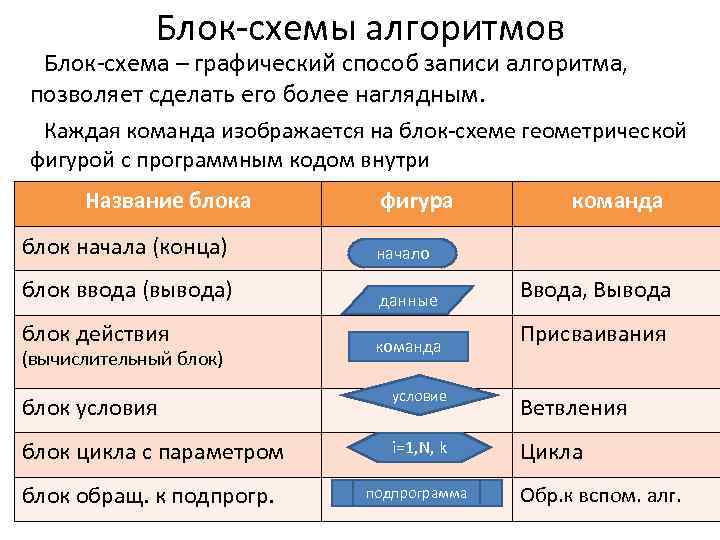
Блок-схемы алгоритмов Блок-схема – графический способ записи алгоритма, позволяет сделать его более наглядным. Каждая команда изображается на блок-схеме геометрической фигурой с программным кодом внутри Название блока фигура команда блок начала (конца) начало блок ввода (вывода) данные Ввода, Вывода блок действия команда Присваивания (вычислительный блок) условие блок условия Ветвления блок цикла с параметром i=1, N, k Цикла блок обращ. к подпрограмма Обр. к вспом. алг.

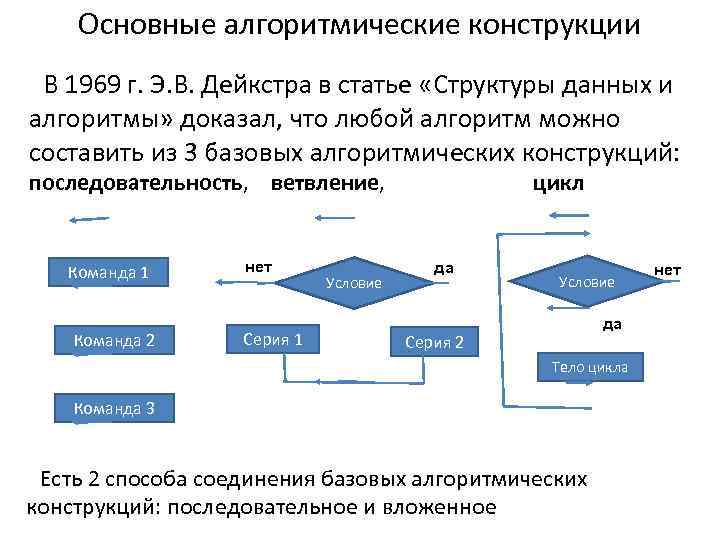
Основные алгоритмические конструкции В 1969 г. Э. В. Дейкстра в статье «Структуры данных и алгоритмы» доказал, что любой алгоритм можно составить из 3 базовых алгоритмических конструкций: последовательность, ветвление, цикл Команда 1 нет да нет Условие да Команда 2 Серия 1 Серия 2 Тело цикла Команда 3 Есть 2 способа соединения базовых алгоритмических конструкций: последовательное и вложенное

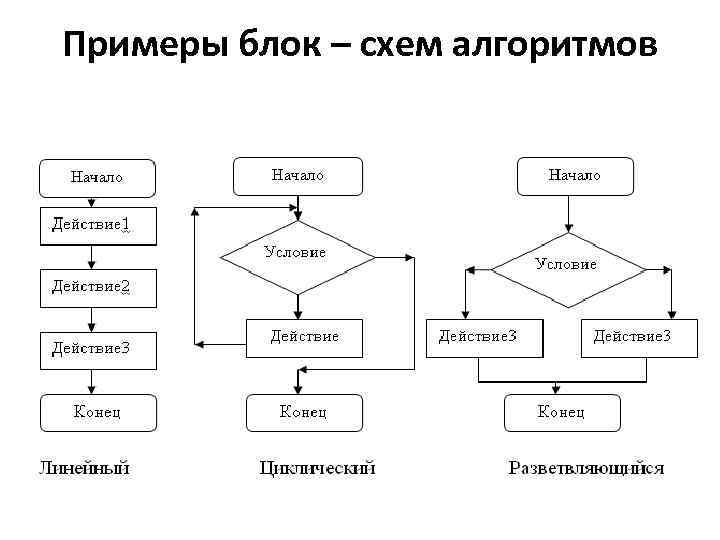
Примеры блок – схем алгоритмов

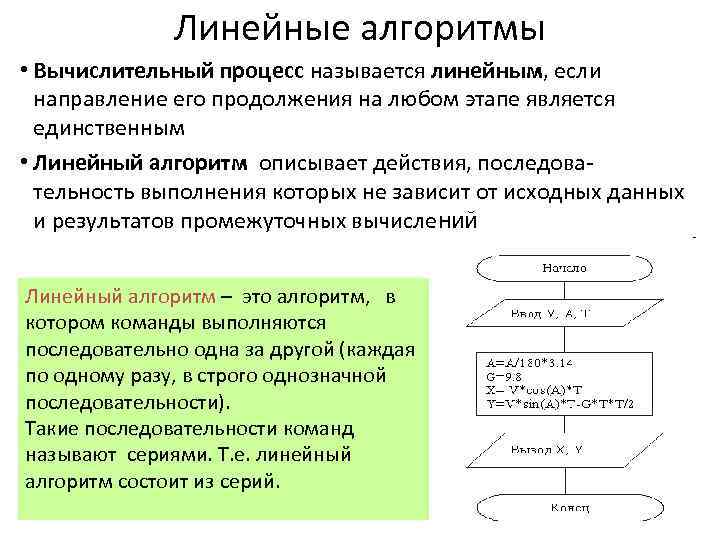
Линейные алгоритмы • Вычислительный процесс называется линейным, если направление его продолжения на любом этапе является единственным • Линейный алгоритм описывает действия, последова- тельность выполнения которых не зависит от исходных данных и результатов промежуточных вычислений Линейный алгоритм – это алгоритм, в котором команды выполняются последовательно одна за другой (каждая по одному разу, в строго однозначной последовательности). Такие последовательности команд называют сериями. Т. е. линейный алгоритм состоит из серий.

Линейные алгоритмы • Запись линейного алгоритма в виде блок-схемы: начало Линейный алгоритм составляется только из действие 1 команд • присваивания • ввода … • вывода • обращения к вспомогательному действие n алгоритму конец

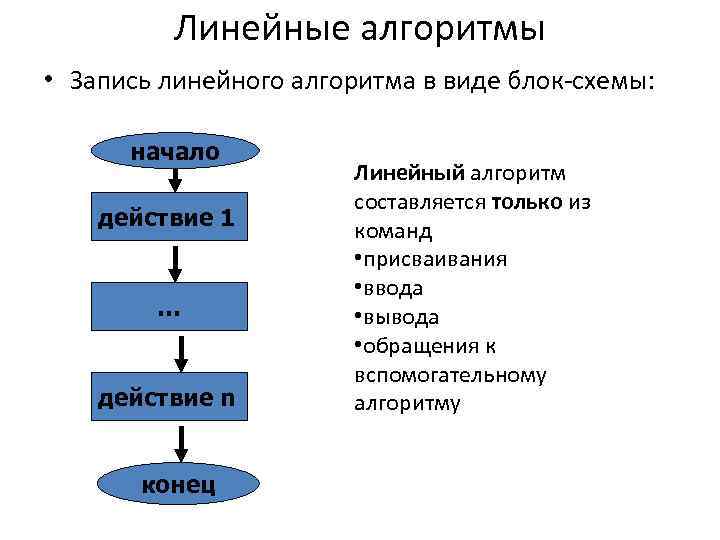
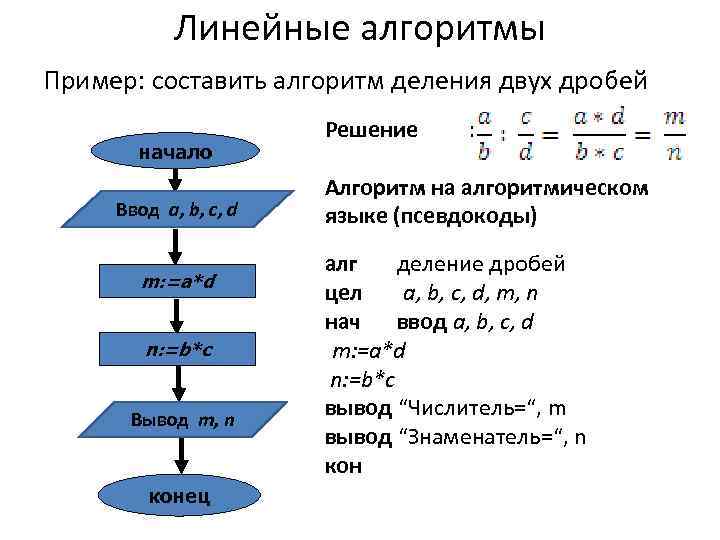
Линейные алгоритмы Пример: составить алгоритм деления двух дробей Решение : начало Алгоритм на алгоритмическом Ввод a, b, c, d языке (псевдокоды) алг деление дробей m: =a*d цел a, b, c, d, m, n нач ввод a, b, c, d n: =b*c m: =a*d n: =b*c Вывод m, n вывод “Числитель=“, m вывод “Знаменатель=“, n конец

Выводы по линейным алгоритмам: • Основным элементарным действием в вычислительных алгоритмах является присваивание значения переменной величине. • Переменная получает конкретное значение только в результате присваивания • Присваивание осуществляется 2 способами – с помощью команды ввода (входные данные) – с помощью команды присваивания (промежуточные данные и результаты) • Свойства команды присваивания: – пока переменной не присвоено значение, ее значение неопределено – значение переменной сохраняется в ней до выполнения нового присваивания – новое значение заменяет старое значение переменной

Задачи на линейные алгоритмы Построить блок-схемы и написать текст на алгоритмическом языке для линейных алгоритмов • Задача 1: Дан радиус окружности, найти длину окружности и площадь круга • Задача 2: Даны три точки на плоскости (x 1, y 1), (x 2, y 2), (x 3, y 3). Найти периметр и площадь получившегося треугольника. • Задача 3: X тетрадей и Y ручек стоят Z рублей, причем известно, что тетрадь на 2 рубля дороже ручки. Сколько стоит 1 ручка и сколько стоит 1 тетрадь?

Домашняя работа на линейные алгоритмы Построить блок-схемы линейных алгоритмов • Задача 1: «Геометрическая задача» - по вариантам (по карточкам). • Задача 2: «Физическая задача» - по вариантам (по карточкам).