ОСНОВЫ АЛГОРИТМИЗАЦИИ 1 Алгоритм понятное и

ОСНОВЫ АЛГОРИТМИЗАЦИИ 1

Алгоритм – понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных данных к конечному результату • Алгоритм – основное понятие, не имеющее формального определения в терминах более простых понятий, оно абстрагируются непосредственно из опыта. 2

Исполнитель алгоритма. • Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом. 3

Свойства алгоритма: • Понятность • Точность • Упорядоченность • Конечность • Дискретность • Эффективность • Массовость 4

Свойства алгоритма: • Понятность – алгоритм должен состоять только из тех команд, которые входят в СКИ. • Точность (определённость, детерминированность) – каждая команда должна быть истолкована исполнителем однозначно • Упорядоченность – строго определённый порядок выполнения действий 5

Свойства алгоритма: • Конечность (финитность, результативность) – выполнение алгоритма должно приводить к решению задачи за конечное число шагов или за конечное число шагов должно быть выдано сообщение, что задача решения не имеет. • Дискретность –процесс решения задачи представляет последовательное выполнение простых (или ранее определенных) шагов. 6

Свойства алгоритма: • Эффективность – решение задачи за приемлемое для разработчика время • Массовость – означает, что алгоритм разработан в общем виде, для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные принадлежат некоторой области, которая называется областью применимости алгоритма. Массовость и эффективность, в отличие от остальных свойств, не являются необходимым свойством алгоритма, но определяют его качество. 7

Способы записи алгоритма: • словесная – запись на естественном языке; • графическая – с помощью блок-схем, диаграмм Насси. Шнейдермана, языка ДРАКОН; • псевдокоды – полуформализованные описания на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др. ; • программная – тексты на языках программирования. 8

Основные алгоритмические структуры Это предположение высказано в 1965 г. Э. Дейкстрой, в том же году итальянские математики К. Бом и Д. Джакопини сформулировали теорему о структурности : Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: • следование • ветвление • цикл 9

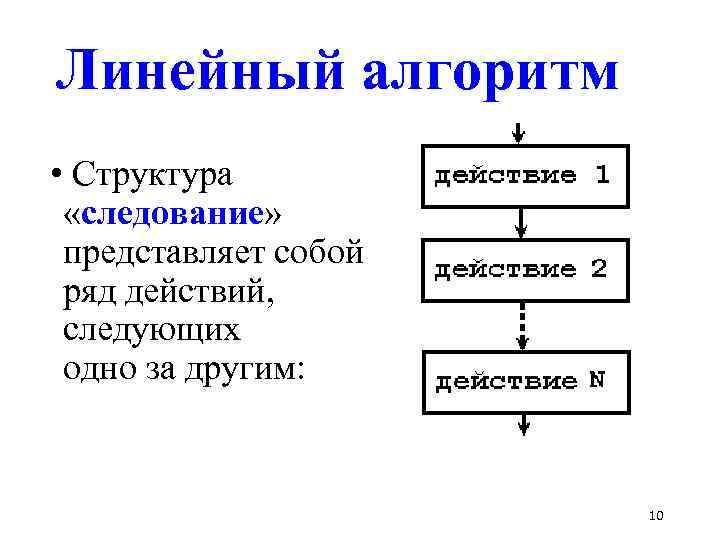Линейный алгоритм • Структура «следование» представляет собой ряд действий, следующих одно за другим: 10

Понятие о логическом выражении Логическое выражение – запись, содержащая логические переменные, логические константы и логические операции. Логическое выражение также может принимать только одно из двух значений (ИСТИНА или ЛОЖЬ), это значение может быть вычислено, если известня значения всех входящих в него логических переменных. 11

Использование логических выражений Применение логических переменных и логических выражений позволяет программисту в ряде случаев использовать не разветвляющийся, а линейный алгоритм. Вместе с тем, для организации ветвления, а также цикла, необходимо использовать логические выражения. 12

Разветвляющийся алгоритм Разветвляющимся называют алгоритм, в котором в зависимости от истинности некоторого условия происходит переход на одну из двух возможных последовательностей действий. Ветвление бывает • полным – каждая из ветвей содержит команды • неполным – в случае истинности условия выполняется некоторая команда, в противном случае – команда пропускается 13

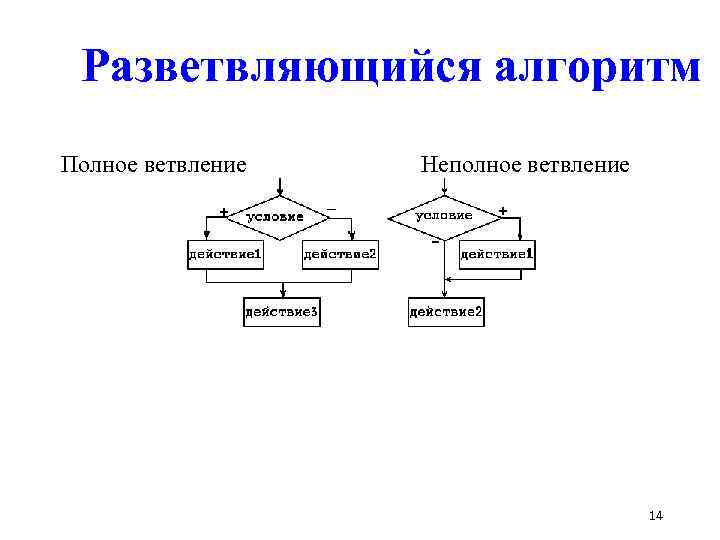Разветвляющийся алгоритм Полное ветвление Неполное ветвление 14

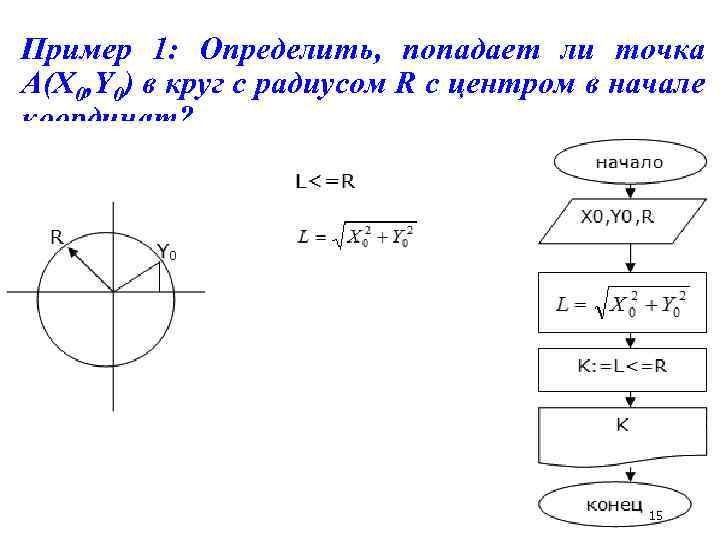Пример 1: Определить, попадает ли точка A(X 0, Y 0) в круг с радиусом R с центром в начале координат? 15

Пример 2: Заданы три числа (a, b, c). Существует ли треугольник с такими сторонами? a b c Логическое выражение, истинное тогда, и только тогда, когда треугольник существует: a

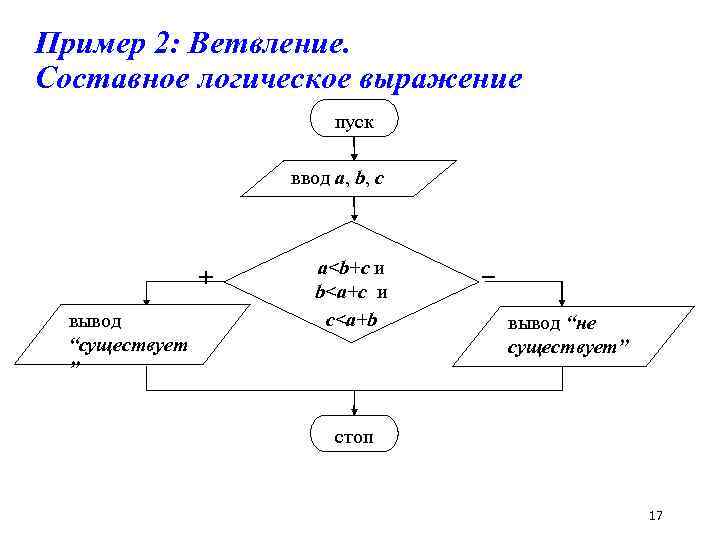Пример 2: Ветвление. Составное логическое выражение пуск ввод a, b, c + вывод “существует ” a

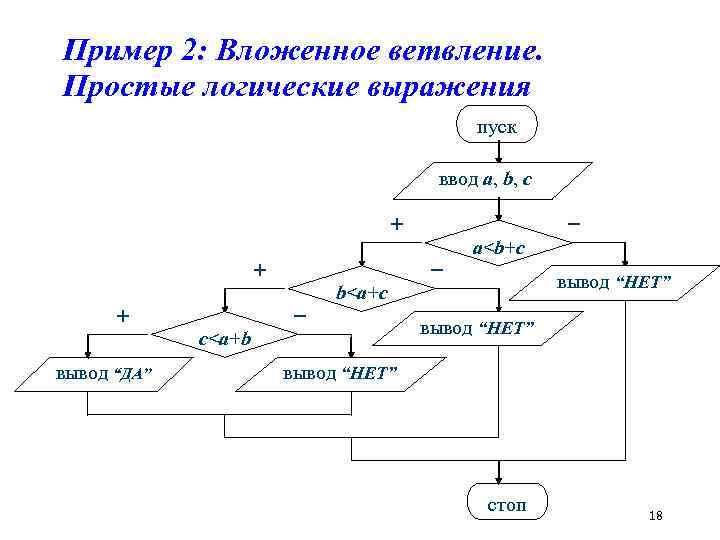Пример 2: Вложенное ветвление. Простые логические выражения пуск ввод a, b, c – + + + – – вывод “НЕТ” b

Резюмируя пример 2 Одна и та же несложная задача может быть решена большим количеством способов. Например, можно использовать линейный алгоритм и одно из двух составных логических выражений (слайд 13), следует только соответствующим образом сформулировать вопрос. При использовании ветвления можно также использовать одно из двух составных логических выражений (слайд 14), а можно – несколько вложенных друг в друга развилок (слайд 15). При этом неравенства также можно заменить на противоположные по смыслу. 19

Резюмируя пример 2 Следует отметить, что в зависимости от набора данных второй способ (слайд 15) может потребовать от одной до трёх проверок простых условий. В большинстве языков программировния вычисление составных логических выражений организовано по так называемому сокращённому варианту: если значение выражения можно определить по первому операнду, то остальные операнды не вычисляются. Например, если первый операнд пои логическом умножении равен false, то вне зависимости от второго операнда результат также равен false. 20

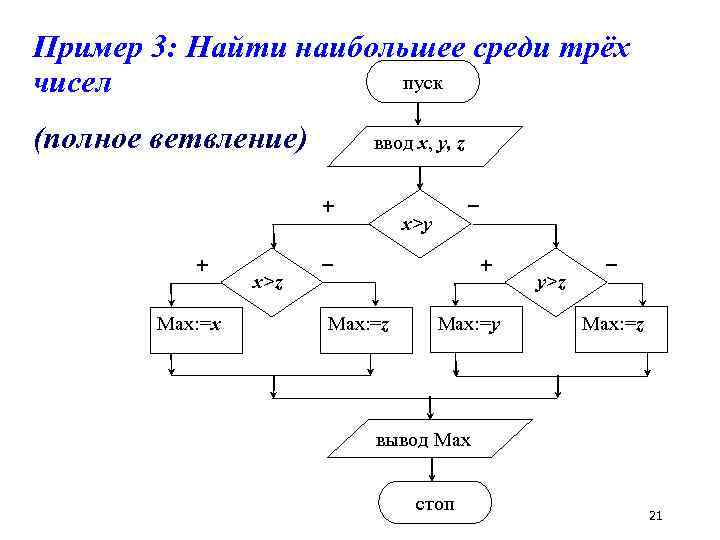Пример 3: Найти наибольшее среди трёх пуск чисел (полное ветвление) ввод x, y, z + + Max: =x x>z – x>y + – Max: =z Max: =y y>z – Max: =z вывод Max стоп 21

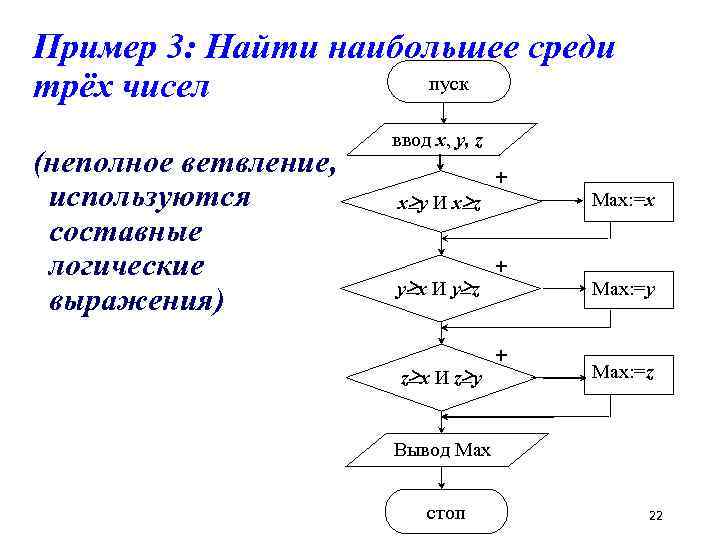Пример 3: Найти наибольшее среди пуск трёх чисел (неполное ветвление, используются составные логические выражения) ввод x, y, z x y И x z y x И y z z x И z y + + + Max: =x Max: =y Max: =z Вывод Max стоп 22

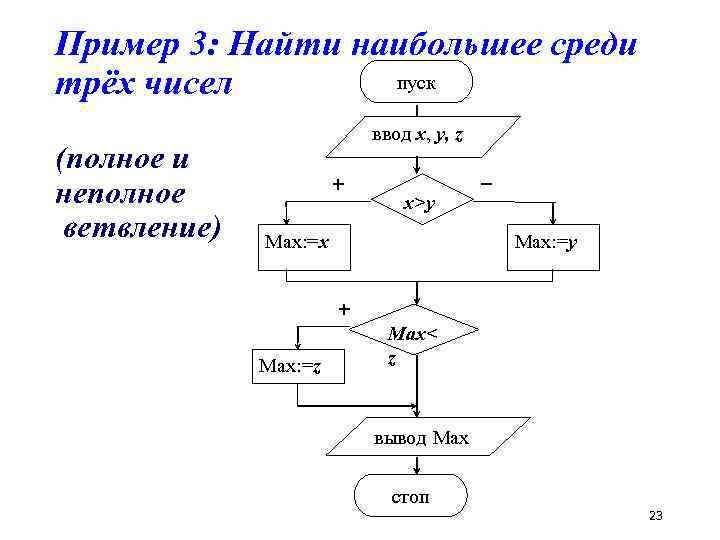Пример 3: Найти наибольшее среди пуск трёх чисел (полное и неполное ветвление) ввод x, y, z + x>y Max: =x – Max: =y + Max: =z Мах< z вывод Max стоп 23

Резюмируя пример 3 Первый способ (слайд 18) решения задачи достигает цели за два ветвления (хотя всего развилок – три). При составлении такого алгоритма следует чётко осознавать, какие условия должны быть вписаны во вложенные развилки, иначе алгоритм может содержать ошибку. Зато нет необходимости записывать составные логические выражения. остигает заспособ ия, Второй цели 19) (слайд условия могут быть перечислены в произвольном порядке, поэтому многим этот способ кажется проще. Однако при этом нужно применять составные условия. 24

Резюмируя пример 3 Третий способ (слайд 20) так же, как и первый, достигает цели за две развилки, но для определённых наборов данных одна из ветвей не требует никаких действий (неполное ветвление). Этот способ может быть модифицирован для поиска максимума среди произвольной последовательности чисел – достаточно положить в Максимум первое число, а затем до тех пор, пока не закончились числа, сравнивать их с Максимумом и в случасе необходимости – затирать Максимум очередным числом 25

Пример 4: Вычислить значение функции f 0(x) f 1(x) x 1 f 2(x) x 2 f 4(x) f 3(x) x 3 x 4 26

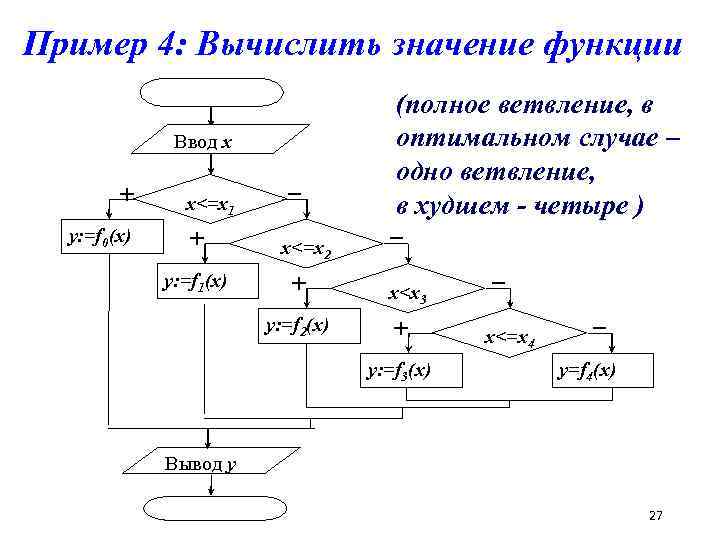Пример 4: Вычислить значение функции Ввод x + y: =f 0(x) x<=x 1 + y: =f 1(x) – x<=x 2 + y: =f 2(x) (полное ветвление, в оптимальном случае – одно ветвление, в худшем - четыре ) – x

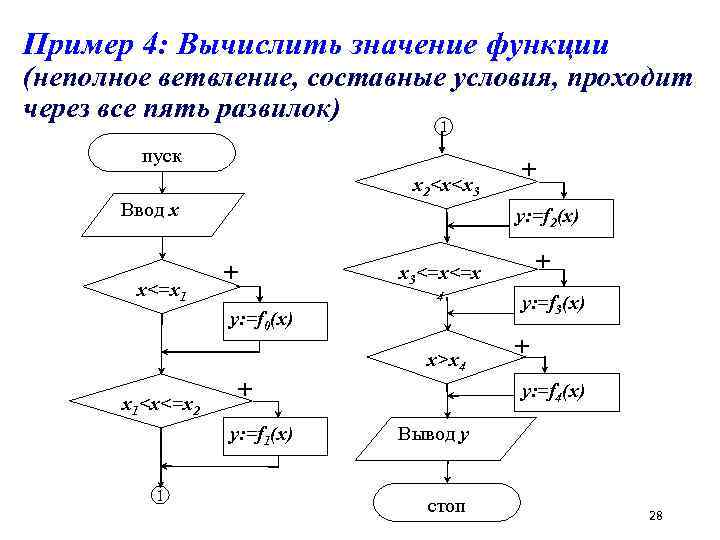Пример 4: Вычислить значение функции (неполное ветвление, составные условия, проходит через все пять развилок) 1 пуск x 2x 4 y: =f 3(x) + y: =f 4(x) Вывод у стоп 28

Резюмируя пример 4 Первый способ (слайд 24) решения задачи достигает цели четыре ветвления в худшем случае и за одно – в оптимальном. При составлении такого алгоритма следует сначала упорядочить точки x 1 … x 4 по возрастанию (или по убыванию). Второй способ (слайд 25) достигает цели всегда за пять ветвлений, условия могут быть перечислены в произвольном порядке, поэтому многим этот способ кажется проще. Однако алгоритм требует большего количества действий. 29

Циклический алгоритм • Обеспечивает многократное выполнение некоторой последовательности действий, которая называется телом цикла. • «Многократно» – не значит «бесконечно» , прекращение циклической последовательности происходит в результате проверки истинности некоторого условия 30

Циклический алгоритм В зависимости от того, когда происходит проверка, различают • Цикл с предусловием • Цикл с постусловием 31

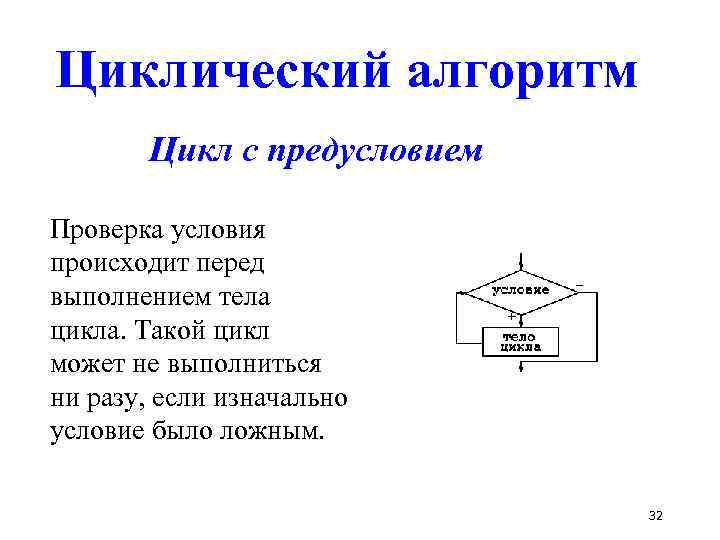Циклический алгоритм Цикл с предусловием Проверка условия происходит перед выполнением тела цикла. Такой цикл может не выполниться ни разу, если изначально условие было ложным. 32

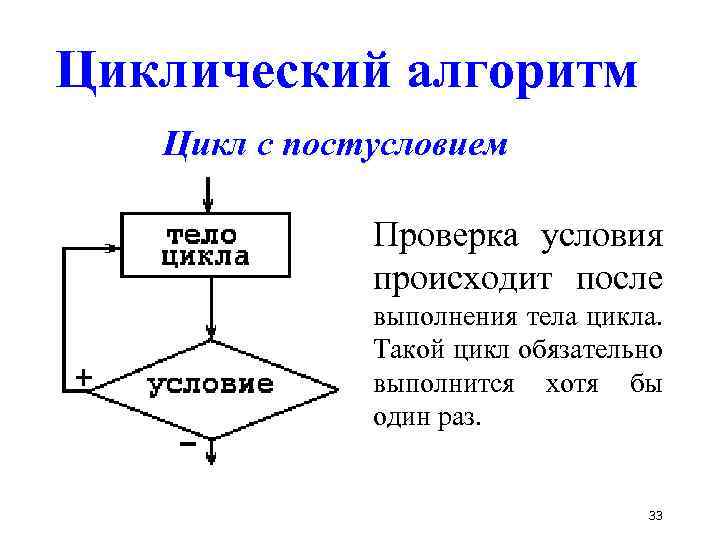Циклический алгоритм Цикл с постусловием Проверка условия происходит после выполнения тела цикла. Такой цикл обязательно выполнится хотя бы один раз. 33

Циклический алгоритм Цикл с параметром (пересчёт, цикл с заданным количеством повторений) • Используется, если заранее известно, сколько раз необходимо выполнить тело цикла. p – параметр, меняется от a до b с шагом с a – начальное значение b – конечное значение с – шаг изменения параметра 34

Типовые задачи, решаемые с использованием циклов: • Нахождение суммы (произведения, среднего арифметического) элементов некоторой последовательности • Подсчёт количества заданных элементов в последовательности • Поиск первого (последнего) элемента последовательности, удовлетворяющего заданному условию • Поиск максимального (минимального) элемента последовательности и другие ПЕРЕБОРНЫЕ задачи 35

Построить алгоритм к следующей задаче: С клавиатуры вводят N чисел. Найти их сумму. Этапы решения 1. Запросить, чему равно N. 2. Обнулить переменную для хранения суммы Sum. 3. Сделать N раз: Запросить у пользователя очередное слагаемое A Прибавить слагаемое A к сумме Sum 4. Вывести результат – значение Sum 36

Построить алгоритм к следующей задаче: С клавиатуры вводят несколько целых чисел, признаком окончания является ввод нуля. Найти сумму введённых чисел Этапы решения: 1. Обнулить переменную для хранения суммы Sum. 2. Повторять: Запросить у пользователя очередное слагаемое A Прибавить слагаемое А к сумме Sum пока A не равно нулю 3. Вывести результат Sum 37

Построить алгоритм к следующей задаче: С клавиатуры вводят несколько целых чисел, признаком окончания является ввод нуля. Найти произведение введённых чисел Этапы решения 1. Переменной для хранения произведения P присвоить значение 1. 2. Запросить у пользователя очередной множитель A. 3. Пока A не равно нулю Умножить произведение P на множитель А Запросить у пользователя очередной множитель A 4. Вывести результат Р 38

Построить алгоритм к следующей задаче: С клавиатуры вводят N чисел. Найти максимальное из них Этапы решения: 1. Запросить, чему равно N. 2. Запросить у пользователя первое число и объявить его максимумом (положить в Мах). 3. Сделать N-1 раз: Запросить у пользователя очередное число A Если A больше, чем Мах, то затереть Мах значением переменной A 4. Вывести результат – значение Мах 39

Построить алгоритм к следующей задаче: С клавиатуры вводят N чисел. Найти порядковый номер максимального из них Этапы решения: 1. Запросить, чему равно N. 2. Запросить у пользователя первое число и объявить его максимумом (положить в Мах). До начала поиска номер максимального элемента N_max равен 1, счётчик равен 2. 3. Пока счётчик не превосходит N, повторять: Запросить у пользователя очередное число A Если A больше, чем Мах, то затереть Мах значением переменной A затереть N_max значением счётчика Увеличить счётчик на 1. 4. Вывести результат – значение Мах 40