Основы Алгебры Логики ВФТШ, Занятие 3 Лакеев Игорь
Алгебра логики, понятие высказывания Алгебра логики - изучает свойства функций, у которых аргументы и значения принадлежат заданному двухэлементному множеству (e. g. {0, 1}) George Boole 1815 -1864
Понятие высказывания • Определение 1 Высказывание – это языковое образование в отношении которого имеет смысл говорить о его истинности и ложности. (Аристотель) • Определение 2 Высказывание называется простым (элементарным), если никакая его часть не является высказыванием.
Итак • Алгебра логики изучает строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
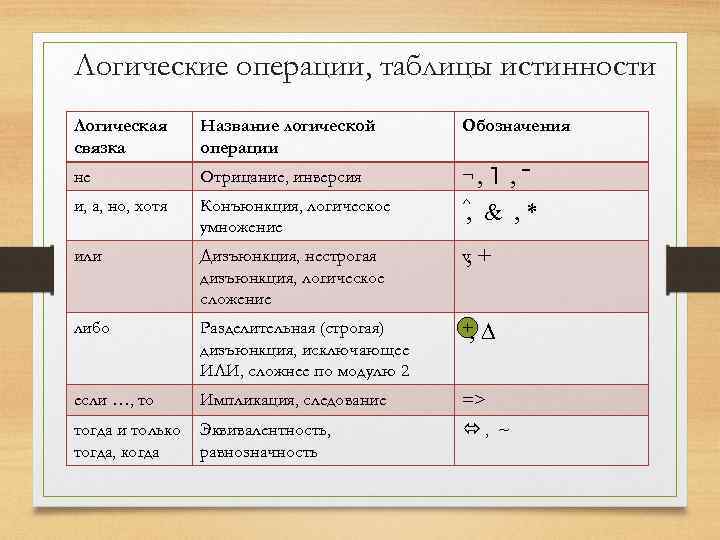
Логические операции, таблицы истинности Логическая связка Название логической операции Обозначения не Отрицание, инверсия ¬, и, а, но, хотя Конъюнкция, логическое умножение ^ или Дизъюнкция, нестрогая дизъюнкция, логическое сложение v , + либо Разделительная (строгая) дизъюнкция, исключающее ИЛИ, сложнее по модулю 2 + , ∆ если …, то Импликация, следование => тогда и только тогда, когда Эквивалентность, равнозначность , ~ ˥ , ‾ , & , *
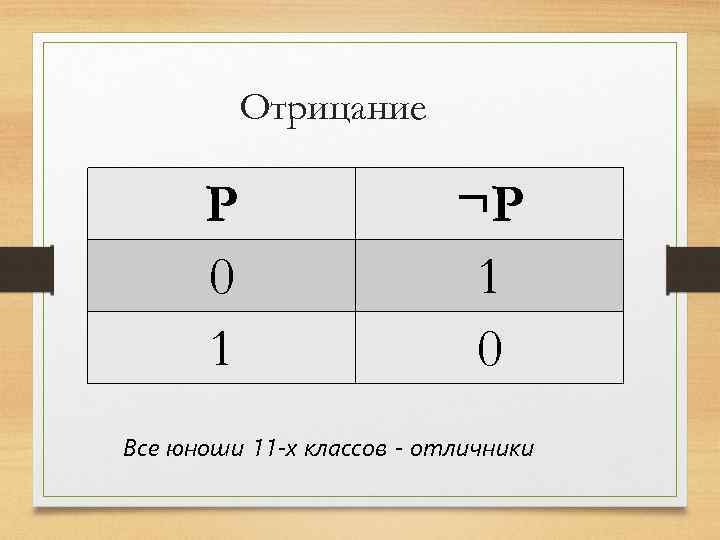
Отрицание P 0 1 ¬P 1 0 Все юноши 11 -х классов - отличники
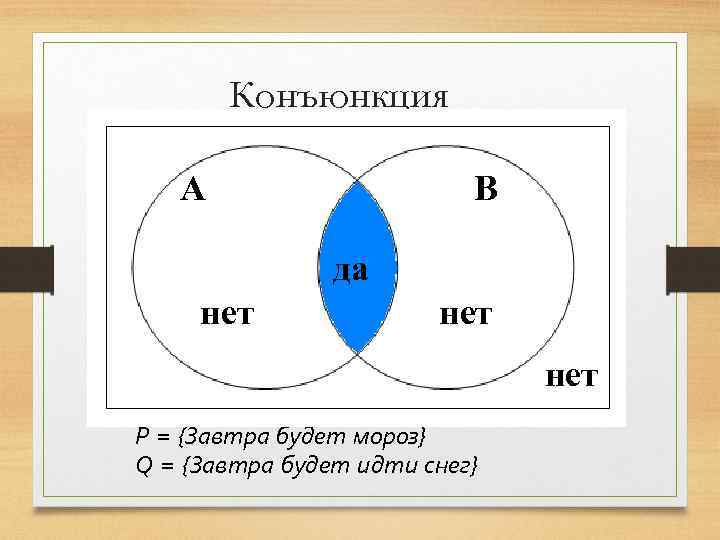
Конъюнкция P А 0 0 нет 1 1 Q 0 да 1 0 1 P&Q В 0 0 нет 1 Р = {Завтра будет мороз} Q = {Завтра будет идти снег}
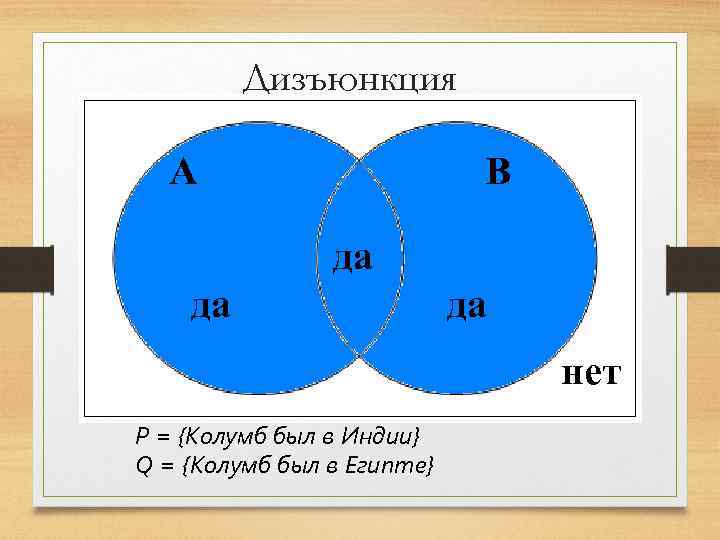
Дизъюнкция P А 0 0 да 1 1 Q 0 да 1 0 1 Р = {Колумб был в Индии} Q = {Колумб был в Египте} Pv. Q В 0 1 да 1 1 нет
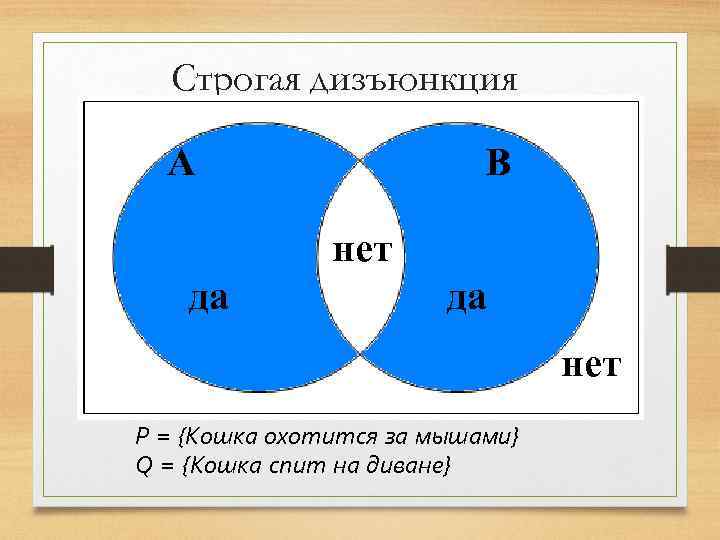
Строгая дизъюнкция P А 0 0 да 1 1 Q 0 нет 1 0 1 P+Q В 0 1 да 1 нет 0 Р = {Кошка охотится за мышами} Q = {Кошка спит на диване}
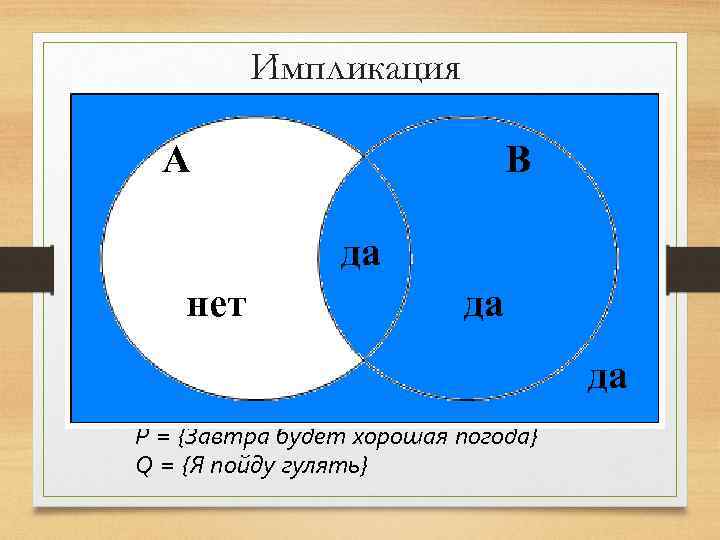
Импликация P А 0 0 нет 1 1 Q 0 да 1 0 1 P => Q В 1 1 да 0 1 да Р = {Завтра будет хорошая погода} Q = {Я пойду гулять}
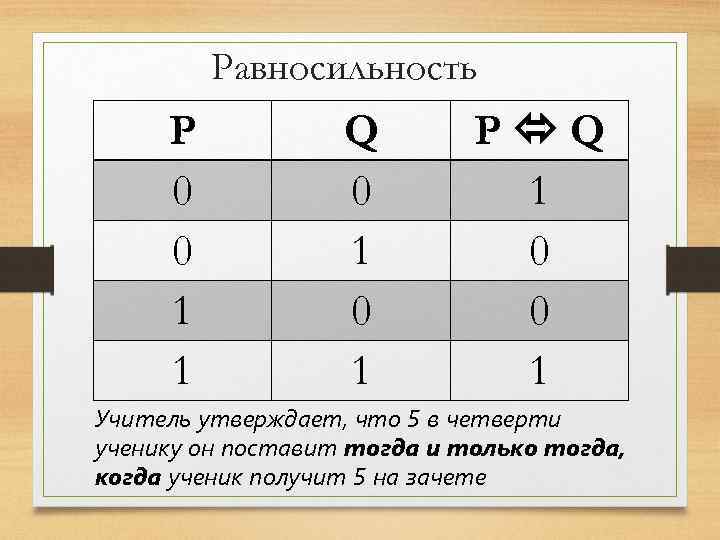
Равносильность P 0 0 1 1 Q 0 1 P Q 1 0 0 1 Учитель утверждает, что 5 в четверти ученику он поставит тогда и только тогда, когда ученик получит 5 на зачете
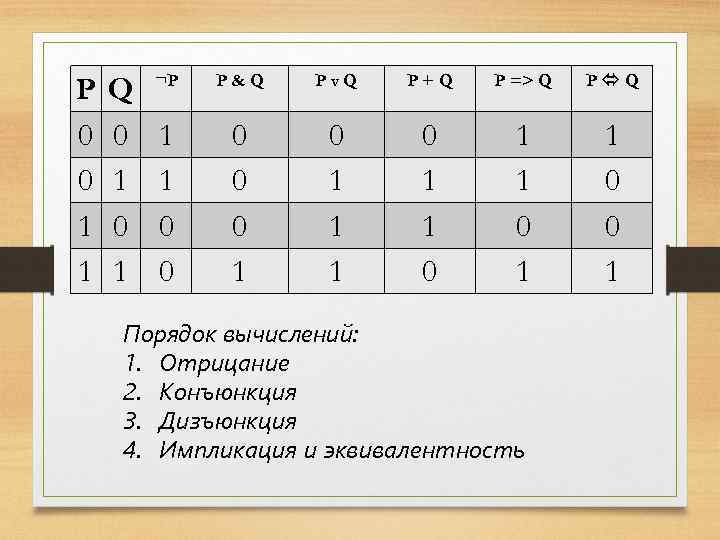
P 0 0 1 1 Q 0 1 ¬P P&Q Pv. Q 1 1 0 0 0 1 1 1 P+Q P => Q Итого 0 1 1 0 1 Порядок вычислений: 1. Отрицание 2. Конъюнкция 3. Дизъюнкция 4. Импликация и эквивалентность P Q 1 0 0 1
Проверим P = {Ане нравятся уроки математики} Q = {Ане нравятся уроки химии} А) P & Q Г) P v Q Б) ¬P & Q Д) P v ¬Q Ж) ¬ (P & Q) К) P => Q З) ¬ (P v Q) В) P & ¬Q Е) ¬P v ¬Q И) ¬ (P & ¬Q) Л) P => ¬Q М) ¬(P => Q)
Логические формулы, законы алгебры логики 1) Законы коммутативности X&Y=Y&X Xv. Y=Yv. X 2) Законы ассоциативности (X & Y) & Z = X & (Y & Z) (X v Y) v Z = X v (Y v Z) 3) Законы поглощения 0 и 1 Xv 0=X X&1=X
Логические формулы, законы алгебры логики 4) Законы дистрибутивности X & (Y v Z) = (X & Y) v (X & Z) X v (Y & Z) = (X v Y) & (X v Z) 5) Закон противоречия X&¬X=0 6) Закон исключения третьего Xv¬X=1 7) Законы идемпотентности X & X = X, X v X = X
Логические формулы, законы алгебры логики 8) Закон двойного отрицания ¬¬X=X 9) Законы де Моргана ¬(X & Y) = ¬X v ¬Y ¬(X v Y) = ¬X & ¬Y 10) Законы поглощения X v (X & Y) = X X & (X v Y) = X
Скачать презентацию Основы Алгебры Логики ВФТШ Занятие 3 Лакеев Игорь
алгебра логики.pptx