Основные характеристики случайной величины Для

Основные характеристики случайной величины

• Для выборки вычисляются следующие основные статистики: • – характеристики расположения (среднее значение медиана , мода ( ) , квантили); • – характеристики рассеяния или изменчивости (дисперсия (S 2), среднее квадратическое отклонение или стандартное отклонение (S), коэффициент вариации (изменчивости) (V), размах (R); • – характеристики асимметрии (А) и эксцесса (Е); • – ошибки отображения (стандартные ошибки) этих показателей, а также находят точность опыта (Р) и необходимое число наблюдений (n). ,

Статистики расположения • Среднее значение признака показывает "центральное положение" (центр) переменной и рассматривается совместно с доверительным интервалом. • Обычно интерес представляют статистики (например, среднее), дающие информацию о популяции в целом. • Чем больше размер выборки, тем более надежна оценка среднего. • Чем больше изменчивость данных (больше разброс), тем оценка менее надежна.

Статистики расположения • Способ вычисления среднего значения зависит от того, что должно характеризовать это среднее. Чаще всего в лесном хозяйстве используется среднее арифметическое значение.

Статистики расположения • Средняя гармоническая применяется тогда, когда результаты наблюдений обнаруживают обратную зависимость, заданы обратными значениями вариант. • Средняя квадратическая применяется для более точной числовой характеристики мер площади. • Средняя кубическая – применяется для объемных объектов. • Средняя геометрическая является более точной характеристикой рядов динамики, чем ар, но отличия, обычно, незначительны. • Соотношения между средними выражаются рядом мажорантности (неравенства): • > >

Статистики расположения Структурные средние • Медиана (Ме) – средняя, относительно которой ряд распределения делится на две равные части: в обе стороны от Ме располагается одинаковое число вариант. Для ее определения, собранные данные ранжируют, и при нечетном числе членов ряда центральная варианта и будет Ме. При четном числе – Ме равно полусумме двух соседних вариант, расположенных в центре от ряда. • Мода (Мо) – величина, наиболее часто встречающаяся в данной совокупности. Класс с наибольшей частотой называется модальным.

Статистики расположения Структурные средние • Квантили – структурные характеристики вариационного ряда, отсекающие в пределах ряда определенную часть его членов. К ним относятся квартили, децили и перцентили. • Квартили – это три значения признака (Q 1, Q 2, Q 3), делящие ранжированный вариационный ряд на четыре части (равные). Аналогично, девять децилей делят ряд на десять равных частей, а девяносто девять перцентилей – на сто равных частей. • В практике используют обычно перцентили Р 3, Р 10, Р 25, Р 50, Р 75, Р 90, Р 97. Р 25 = Q 1, Р 75 = Q 3, Р 50 = Q 2 = Ме.

Показатели вариации (изменчивости) • Размахом (R) называется разность между наибольшим и наименьшим значениями признака: R = xmax – xmin. • Чем сильнее варьирует признак, тем больше размах вариации и наоборот. • Лимиты – минимальные и максимальные варианты. • Лимиты и размах вариации – простые и наглядные характеристики варьирования, но у них есть существенные недостатки: при повторных измерениях одного и того же объекта они могут значительно изменятся; кроме того, они не отражают существенных черт варьирования.

Показатели вариации (изменчивости) • Дисперсия (S 2) показывает степень изменчивости вариант, меру их концентрации вокруг среднего значения и находится по формулам: – для бесчастотной выборочной совокупности, – для данных с частотами. • Чем выше дисперсия, тем сильнее разброс отдельных вариант вокруг среднего значения.

Показатели вариации (изменчивости) • Стандартное отклонение (среднее квадратическое отклонение) показывает величину среднего отклонения отдельных вариант от среднего значения признака. • Преимущество среднего квадратического перед дисперсией состоит в том, что оно выражается в тех же единицах измерения, что и среднее значение признака. • Чем больше значение среднего квадратического отклонения, тем варианты сильнее рассеяны около средней величины, то есть тем выше степень варьирования изучаемого явления.

Показатели вариации (изменчивости) • Около 68 процентов всех вариант нормально распределенной случайной величины отклоняется от генеральной средней не более, чем на одно среднее квадратическое отклонение. • Около 99, 73% – не более, чем на утроенное среднее квадратическое отклонение. На этой закономерности основано правило "трех сигм". (Для генеральной совокупности среднее квадратическое отклонение принято обозначать греческой буквой «сигма» - σ. ). • По этому правилу в предположении, что генеральная совокупность распределена нормально, варианты, которые отклоняются от среднего значения более чем на ± 3σ , из обработки исключаются как принадлежащие к другой генеральной совокупности. • Имеется и другое применение этого правила. Если распределение случайной величины не известно, но условие, указанное в правиле "трех сигм", выполняется, то можно предположить нормальное распределение случайной величины.

Показатели вариации (изменчивости) • Коэффициентом изменчивости (вариации) называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней: • Он характеризует те же свойства совокупности, что и среднее квадратическое отклонение. Преимущество коэффициента изменчивости заключается в том, что он является безразмерной величиной, и поэтому он удобен для сравнения рассеяния признаков, имеющих разные единицы измерения. • Недостатком является невозможность нахождения V при х, равных нулю (или близких к нему).

Показатели вариации (изменчивости) • На основании величины коэффициента изменчивости можно установить словесную характеристику изменчивости: V до 5% 6 -10% 11 -20% 21 -50% >51% Изменчивость слабая умеренная значительная большая очень большая

Показатели асимметрии и эксцесса • Нормированный 3 -й центральный момент называется коэффициентом асимметрии и служит характеристикой асимметрии или скошенности распределения: А = μ 3 /S 3. • Если случайная величина распределена симметрично относительно своего математического ожидания (среднего значения), то А = 0. Если «хвост» справа – А > 0, «хвост» слева – А < 0 (рис. 2 ). • С 4 -м центральным моментом связана величина, называемая коэффициентом эксцесса: Е = μ 4 /S 4 – 3. • Эксцесс характеризует островершинность или плосковершинность распределения. Для нормального закона распределения Е = 0. Кривые более островершинные, чем нормальная – положительны; более плосковершинные – отрицательные (рис. 3)

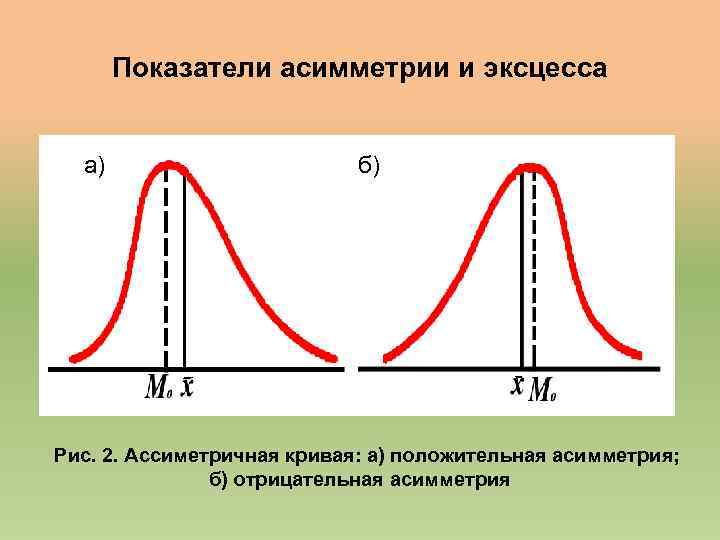Показатели асимметрии и эксцесса а) б) Рис. 2. Ассиметричная кривая: а) положительная асимметрия; б) отрицательная асимметрия

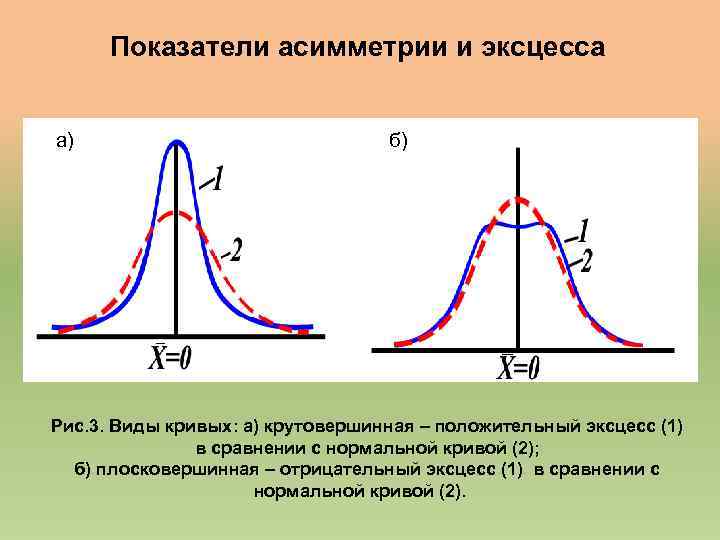Показатели асимметрии и эксцесса а) б) Рис. 3. Виды кривых: а) крутовершинная – положительный эксцесс (1) в сравнении с нормальной кривой (2); б) плосковершинная – отрицательный эксцесс (1) в сравнении с нормальной кривой (2).

Ошибки отображения

Точность опыта • или

Необходимое число наблюдений где t 0, 68 = 1, t 0, 95 = 1, 96, t 0, 99 =2, 58.