Основные выборочные характеристики Числовые характеристики выборки дают

Основные выборочные характеристики

Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой. Наибольшее практическое значение имеют характеристики положения (среднее арифметическое, мода, медиана), рассеивания и ассиметрии статистических распределений.

Статистическая совокупность содержит некоторое количество величин, имеющих разные значения и признаки, что делает невозможным их сравнение в целом. Для этой цели применяют среднюю величину, как обобщающий показатель, характеризующий изучаемый процесс. Ср. величина обобщает количественное выражение признака, погашает индивидуальные различия стат. величин совокупности, вызванные случайными обстоятельствами.

В зависимости задания вариационного ряда разделяют 3 способа вычисления средней: 1. Несгруппированный дискретный ряд - простое среднее 2. Сгруппированный ряд – взвешенное среднее 3. Интервальный сгруппированный ряд – взвешенное среднее

Среднее арифметическое – значение признака, сумма отклонений от которого выборочных значений признака равна нулю (с учётом знака отклонения): где n - объём выборки.

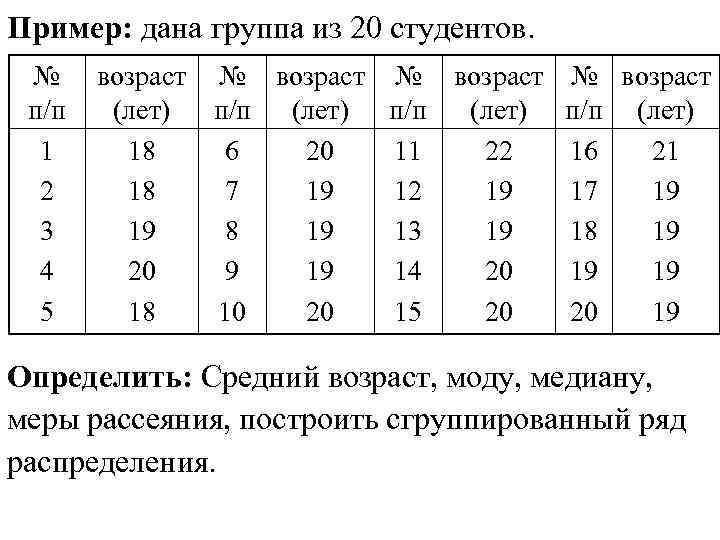
Пример: дана группа из 20 студентов. № п/п 1 2 3 4 5 возраст № возраст (лет) п/п (лет) 18 6 20 11 22 16 21 18 7 19 12 19 17 19 19 8 19 13 19 18 19 20 9 19 14 20 19 19 18 10 20 15 20 20 19 Определить: Средний возраст, моду, медиану, меры рассеяния, построить сгруппированный ряд распределения.

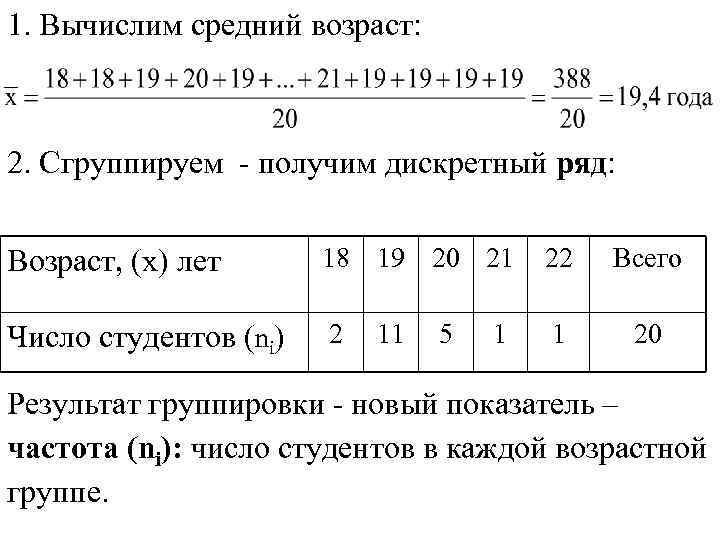
1. Вычислим средний возраст: 2. Сгруппируем - получим дискретный ряд: Возраст, (x) лет 18 19 20 21 22 Всего Число студентов (ni) 2 1 20 11 5 1 Результат группировки - новый показатель – частота (ni): число студентов в каждой возрастной группе.

Средний возраст студентов - взвешенная средняя:

Средняя квадратическая - если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет квадратической:

Пример: имеются участки земли со сторонами: х1 = 100 м; х2 = 200 м; х3 =300 м. Заменяя значения длины сторон на среднюю, нужно исходить из сохранения общей площади участков: арифм. средняя (100+200+ 300): 3 =200 м не удовлетворяет условию, т. к. общая площадь: 3∙(200 м)2 = 120 000 м 2. А площадь: (100 м)2 + (200 м)2 + (300 м)2 = 140 000 м. Ответ дает квадр. средняя:

Средняя геометрическая - если при замене величин признака на среднюю необходимо сохранить неизменным произведение индивидуальных величин, то применяют геометрическую среднюю:

Пример: В результате инфляции за первый год цена товара возросла в 2 раза к предыдущему, а за второй год еще в 3 раза к уровню предыдущего. Каков средний темп роста цены за год? Решение: За два года цена выросла в 6 раз. Арифм. средняя непригодна: если за год цены возросли бы в (2 + 3)/2 = 2, 5 раза, то за два года цена возросла бы в 2, 5× 2, 5 = 6, 25 раза, а не в 6 раз. Геометрическая дает правильный ответ:

Геометрическая средняя дает наиболее правильный по содержанию результат осреднения, если задача в нахождении такого значения признака, который качественно равноудален как от максимального, так и от минимального значения. Например, если максим. размер выигрыша в лотерее составляет миллион руб. , минимальный - сто руб. , то какую величину выигрыша можно считать средней?

Арифм. средняя непригодна = 500 050 руб. - как и миллион, крупный, никак не средний выигрыш; он качественно однороден с max и резко отличен от min. Не дают верного ответа ни квадратическая (707 107 руб. ), ни кубическая (793 699 руб. ), ни гармоническая (199, 98 руб. ), слишком близкая к min. значению. Геометрическая средняя 10000 руб. - правильный ответ.

Средняя гармоническая - если необходимо, чтобы неизменной оставалась при осреднении сумма величин, обратных индивидуальным значениям признака. Если веса у каждого значения признака равны, то используют ср. гармоническую: На практике чаще применяют взвешенную гармоническую при расчете общей средней из средних групповых.

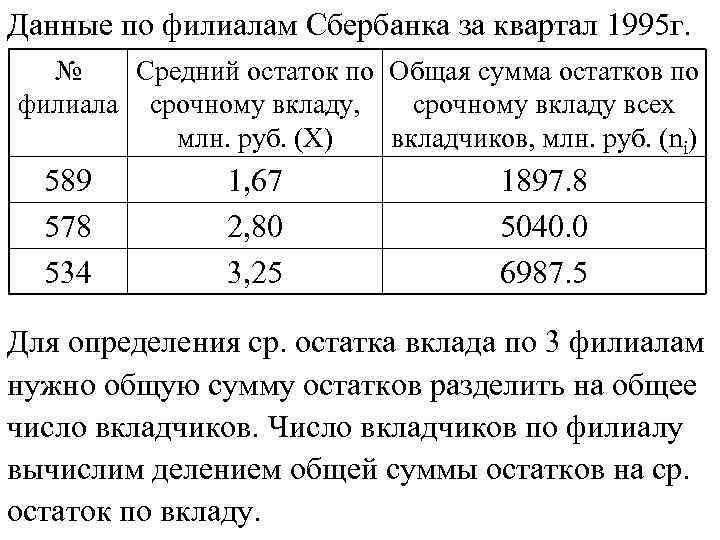
Данные по филиалам Сбербанка за квартал 1995 г. № Средний остаток по Общая сумма остатков по филиала срочному вкладу, срочному вкладу всех млн. руб. (Х) вкладчиков, млн. руб. (ni) 589 578 534 1, 67 2, 80 3, 25 1897. 8 5040. 0 6987. 5 Для определения ср. остатка вклада по 3 филиалам нужно общую сумму остатков разделить на общее число вкладчиков. Число вкладчиков по филиалу вычислим делением общей суммы остатков на ср. остаток по вкладу.

Вывод: Если имеется стат. распределение по двум взаимосвязанным показателям, для одного из которых надо вычислить среднюю (при этом известен итог числителя, итог знаменателя не известен, но определяется как сумма частных от деления значений одного показателя на другой), средняя должна вычисляться по формуле ср. гарм. взвешенной (!).

Рассмотренные виды средних принадлежат к общему типу степенных средних (различаются показателем степени k): корень k-й степени из частного от деления суммы индивидуальных значений признака в k-й степени на число индивидуальных значений:

При k = 1 - арифметическая, k =2 - квадратическая, k = 3 - кубическая, k = 0 - геометрическая, k = -1 - гармоническая средняя. Чем выше показатель k, тем больше значение средней - правило мажорантности:

Пример: Вычислить средний балл успеваемости студента получившего на аттестации оценки 2 и 5. Решение: 1. арифметическая 3, 5 балла 2. гармоническая 3. кубическая

Медиана (Me, med) - значение признака, которое делит выборочную совокупность (вариационный ряд) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

1) Объем выборки n – нечетное число: медиана равна варианте признака, имеющей номер 2) Объем выборки n – четное число: медиана определяется как полусумма из вариант, имеющих номера

Медиану можно определить графически, по кумуляте. Для этого последнюю ординату, равную сумме всех частот или частостей, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы. Кумуляту строят по накопленным частотам (или частостям), которые откладывают по оси у, по оси х – варианты или верхние границы интервалов

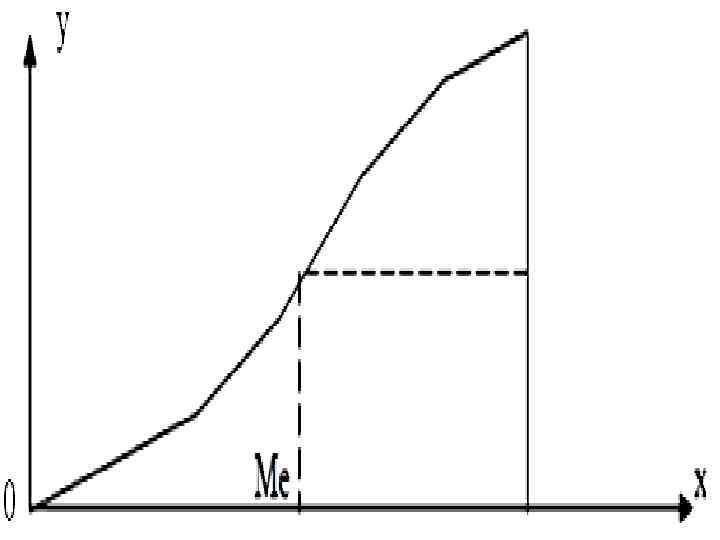
При вычислении медианы в интервальном ряду сначала находят медианный интервал (т. е. содержащий медиану) по накопленным частотам или частостям. Медианным является первый интервал, накопленная частота которого превышает половину объема совокупности.

Если сумма накопленных частот одного из интервалов равна точно половине суммы частот ряда, то медиана:

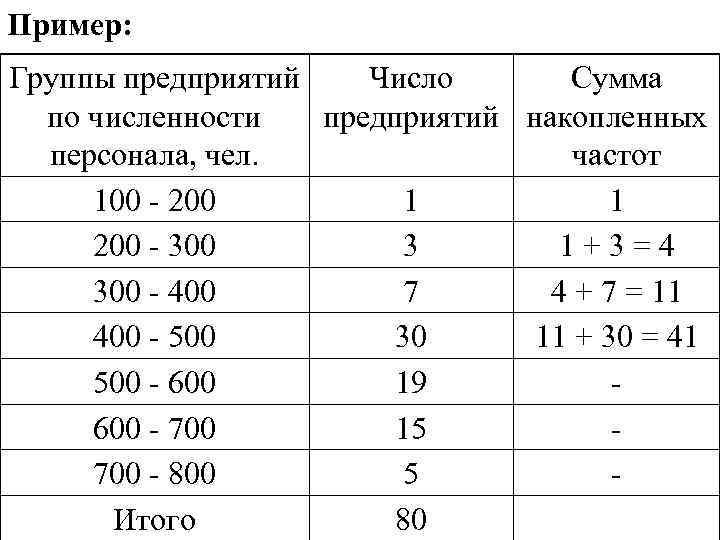
Пример: Группы предприятий Число Сумма по численности предприятий накопленных персонала, чел. частот 100 - 200 1 1 200 - 300 3 1 + 3 = 4 300 - 400 7 4 + 7 = 11 400 - 500 30 11 + 30 = 41 500 - 600 19 600 - 700 15 700 - 800 5 Итого 80

По данным о распределении предприятий по численности персонала рассчитать медиану в интервальном вариационном ряду. Решение: Определим медианный интервал - сумма накопленных частот, превышающих половину суммы всех значений ряда, соответствует интервалу от 400 до 500 чел. , котором находится медиана ряда. Определим её значение.

Пример: сумма накопленных частот против одного из интервалов равна точно половине суммы частот ряда - по имеющимся данным о распределении предприятий по численности промышленно – производственного персонала рассчитать медиану.

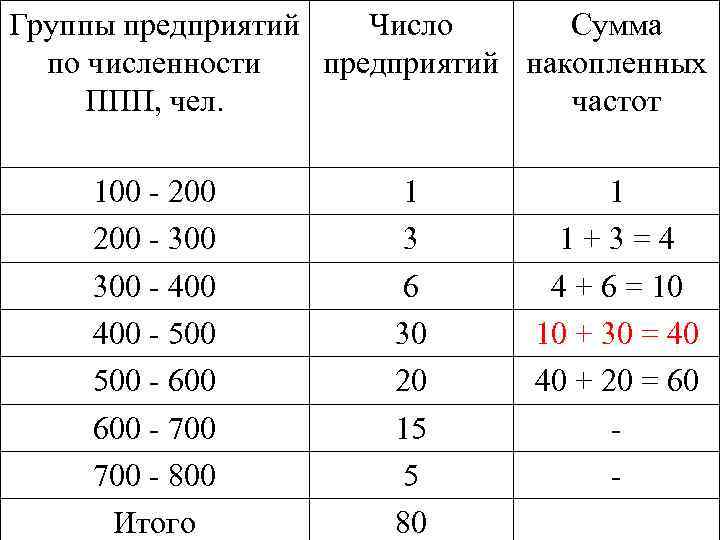
Группы предприятий Число Сумма по численности предприятий накопленных ППП, чел. частот 100 - 200 - 300 - 400 - 500 - 600 - 700 - 800 Итого 1 3 6 30 20 15 5 80 1 1 + 3 = 4 4 + 6 = 10 10 + 30 = 40 40 + 20 = 60 -

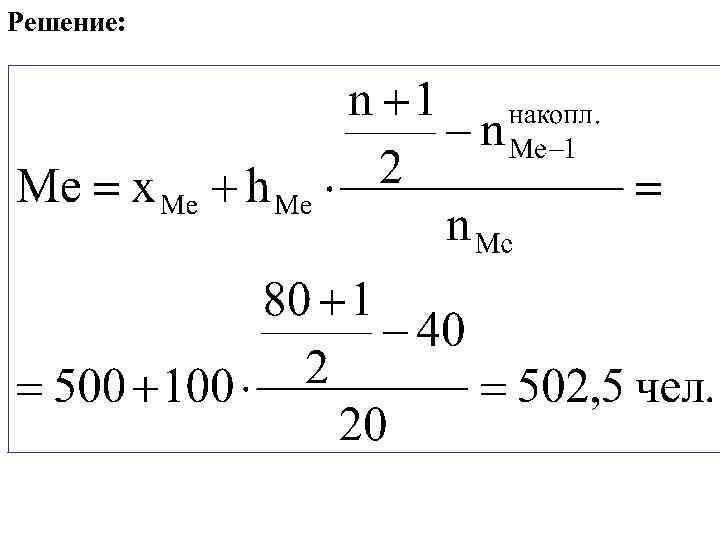
Решение:

Мода - значение признака, которое встречается наиболее часто (имеет наибольшую частоту). Иногда выборка содержит более чем одну моду (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае говорят, что совокупность мультимодальна. Мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.

Мода употребляется для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства. В нашем случае мода Мо= 19 годам наибольшее число студентов (n 19 = 11) имеют такой возраст.

В интервальных рядах распределения для нахождения моды сначала по наибольшей частоте определяют модальный интервал (интервал, содержащий моду), а затем ее рассчитывают:

где x Mo – нижняя граница модального интервала; h Mo – длина (шаг) модального интервала; n Mo - частота модального интервала. n Mo-1, n. Mo+1 - частоты, соответственно в предыдущем и следующим за модальным интервалах.

Пример: Распределение рабочих по стажу работы характеризуется следующими данными. Стаж работы, лет Число рабочих, чел. <2 2 -4 4 -6 6 -8 8 -10 >10 4 23 20 35 11 7 Определить моду ряда распределения. Решение: модальный интервал – число рабочих со стажем от 6 до 8 лет, x Mo= 6; h Mo = 8 – 6 = 2; n Mo= 35; n Mo-1= 20; n Mo+1= 11.

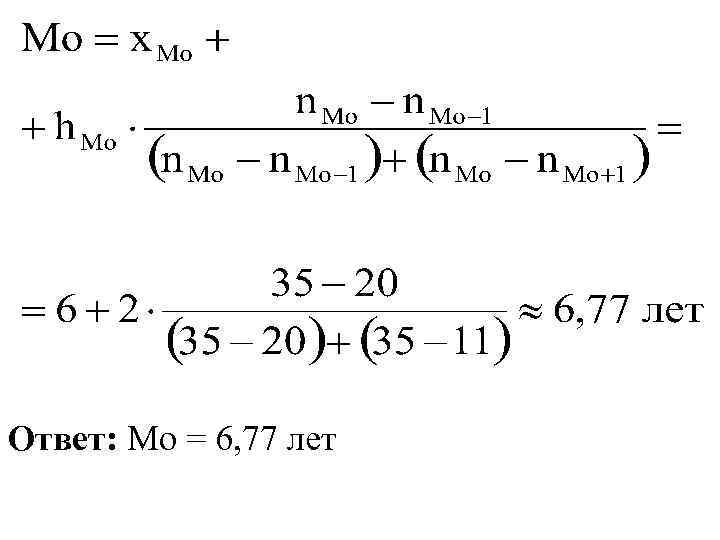
Ответ: Мо = 6, 77 лет

Характеристики рассеяния Средние значения не дают полной информации о варьирующем признаке. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки.

Размах вариации (R) – разность между максимальной и минимальной вариантами выборки: R = |xmax - xmin| Дисперсия или стандартное отклонение – (лат. dispersio - рассеяние) - мера рассеивания (отклонения от среднего). В статистическом понимании дисперсия есть среднее арифметическое из квадратов отклонений величин xi от их среднего арифметического.

Вычисление: из каждой варианты вычитают среднюю арифметическую, разность возводят в квадрат и умножают на соответствующую ей частоту.

Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то получим формулу для её расчета как разность средней квадратов и квадрата средней:

Среднее квадратическое отклонение σ – корень квадратный из дисперсии. Размерность σ совпадает с единицами измерения варьирующего признака, поэтому это самая распространенная характеристика рассеивания.

Важный показатель, характеризующий вариацию признака, - коэффициент вариации (отношение стандартного отклонения к среднему арифметическому, выраженное в процентах): По величине коэффициента V судят о степени вариации признаков: чем больше его величина, тем больше разброс значений вокруг средней, менее однородна совокупность по составу и тем менее представительна средняя.

Принято различать градации изменчивости: незначительная умеренная сильная чрезмерная V ≤ 5% 5%< V ≤ 15%<V ≤ 33% <V Совокупность считают количественно однородной, если величина V ≤ 33%. Вывод. Величина рассчитанного коэффициента свидетельствует о незначительной изменчивости индивидуальных значений в выборке. Совокупность можно считать однородной, а её среднюю – надёжной.

Этот показатель важен в тех случаях, когда нужно сравнивать средние квадратические отклонения различных совокупностей, выраженные изначально в разных единицах измерения (!!!).

КОНЕЦ ФИЛЬМА