Основные вопросы Методы анализа цепей постоянного тока продолжение

Основные вопросы: Методы анализа цепей постоянного тока (продолжение): 8. Метод эквивалентного источника тока 9. Линия электропередачи постоянного тока Переходные процессы в линейных электрических цепях постоянного тока: 1. Понятие переходного процесса 2. Причины возникновения переходных процессов. Законы коммутации 3. Математические основы анализа переходных процессов: − классический метод анализа переходных процессов; − операторный метод анализа переходных процессов.

8. Метод эквивалентного источника тока Суть метода: Дана электрическая цепь и значения всех элементов. Нужно найти только один ток I в заданной ветви ab. План анализа: 1. Произвольно выбрать положительное направление искомого тока I ветви ab 2. Составить схему, заменив ветвь ab короткозамкнутым отрезком. Направление тока короткого замыкания Ik выбрать совпадающим с направлением тока I. Вычислить любым методом ток Ik. Составить равенство JЭК = Ik. 3. Составить схему для вычисления RЭК. Для этого используют схему из п. 2, в которой источники ЭДС заменяют короткозамкнутыми отрезками. Источники тока отключают. Если источники имеют внутреннее сопротивление, то их сопротивления должны оставаться в схеме. Используя эквивалентные преобразования, вычислить RЭК относительно разомкнутых зажимов ab. 4. Составить цепь с подключённой ветвью ab. При этом направление JЭК на схеме должно быть противоположным с направлением Ik в исходной схеме. 5. Используя метод уравнений Кирхгофа, найти искомый ток

Пример 1. Определить значение тока I 2 в цепи методом эквивалентного источника тока при Е 1 = 1 В, Е 2 = 3 В, Е 3 = 5 В, R 1 = 2 Ом, R 2 = 4 Ом, R 3 = 2 Ом. Решение. Разделим схему на две части, границей для которых будут точки a и b. Произведем замену активного двухполюсника на источник напряжения. Определяем значение Rэк Производим замену активного двухполюсника на эквивалентный источник напряжения

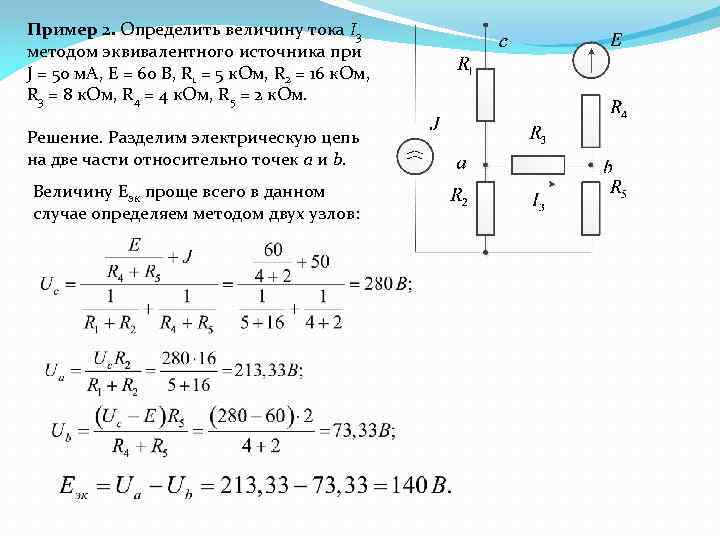Пример 2. Определить величину тока I 3 методом эквивалентного источника при J = 50 м. А, Е = 60 В, R 1 = 5 к. Ом, R 2 = 16 к. Ом, R 3 = 8 к. Ом, R 4 = 4 к. Ом, R 5 = 2 к. Ом. Решение. Разделим электрическую цепь на две части относительно точек а и b. Величину Еэк проще всего в данном случае определяем методом двух узлов:

Теперь определим Rэк Производим замену активного двухполюсника на эквивалентный источник напряжения:

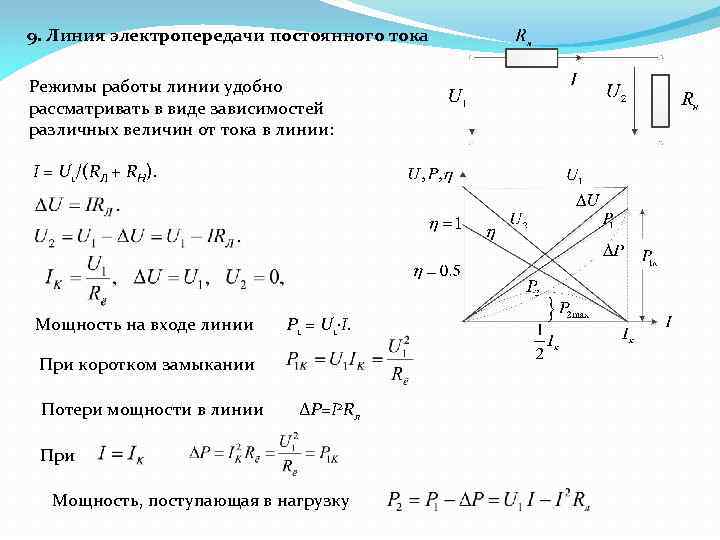9. Линия электропередачи постоянного тока Режимы работы линии удобно рассматривать в виде зависимостей различных величин от тока в линии: I = U 1/(RЛ + RH). Мощность на входе линии P 1 = U 1 I. При коротком замыкании Потери мощности в линии ΔP=I 2 Rл При Мощность, поступающая в нагрузку

Мощность нагрузки Мощность, передаваемая нагрузке, максимальна при При этом Коэффициент полезного действия или, поскольку а то т. е. потери ΔР пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения.

Переходные процессы в линейных электрических цепях постоянного тока Основные вопросы: 1. Понятие переходного процесса 2. Причины возникновения переходных процессов. Законы коммутации 3. Математические основы анализа переходных процессов 4. Алгоритм расчета переходных процессов классическим методом 5. Переходные процессы в цепях с первого порядка 6. Переходные процессы в цепях второго порядка 7. Переходные процессы в цепях с резистором, конденсатором и катушкой индуктивности

Переходные процессы в линейных электрических цепях постоянного тока 1. Понятие переходного процесса (режима) Установившиеся процессы, которые устанавливаются в цепи при неизменных напряжении, токе, сопротивлении и др. Переходные (динамические, нестационарные) процессы перехода электрической цепи из одного установившегося состояния (режима) в другое. Задача исследования переходных процессов : по какому закону и как долго будет наблюдаться заметное отклонение токов в ветвях и напряжений на участках цепи от их установившихся значений. Переходные процессы: возникают при изменениях режима электрической цепи: подключении и отключении, изменении нагрузки, возникновении аварийных режимов (короткое замыкание, обрыв провода и т. д. ). обычно быстропротекающие: длительность их составляет десятые, сотые, а иногда и миллиардные доли секунды.

Переходные процессы в линейных электрических цепях постоянного тока 2. Причины возникновения переходных процессов. Законы коммутации Резистор R, Ом Конденсатор С, Ф Q = C u i(t) = dq/dt При С = const Катушка индуктивности При L = const Ф = Li u(t) = d. Ф/dt

Переходные процессы в линейных электрических цепях постоянного тока Законы коммутации Переходные процессы могут возникать, если в цепи есть индуктивные и(или) емкостные элементы. При подключении внешних источников энергии происходит перераспределение энергии между индуктивными, емкостными элементами цепи и внешними источниками энергии, подключенными к цепи. После окончания переходного процесса устанавливается новый установившийся режим, который определяется только внешними источниками энергии. При отключении внешних источников энергии переходный процесс может возникать за счет энергии электромагнитного поля, накопленной до начала переходного режима в индуктивных и емкостных элементах цепи. Изменения энергии магнитного и электрического полей не могут происходить мгновенно, и, следовательно, процессы не могут протекать мгновенно в момент коммутации (для этого необходимо иметь бесконечно большую мощность!).

Переходные процессы в линейных электрических цепях постоянного тока Так как энергия магнитного WМ и электрического WЭ полей описывается выражениями: то ток в индуктивности и напряжение на емкости не могут изменяться мгновенно. Первый закон коммутации: ток в ветви с индуктивным элементом в начальный момент после коммутации имеет то же значение, какое он имел непосредственно перед коммутацией, а затем с этого значения он начинает плавно изменяться: i. L(0 -) = i. L(0+). Иначе – ток в индуктивности не может измениться скачком. Второй закон коммутации: напряжение на емкостном элементе в начальный момент после коммутации имеет то же значение, какое оно имело непосредственно перед коммутацией, а затем с этого значения оно начинает плавно изменяться: UC(0 -) = UC(0+). Иначе – напряжение на емкости не может измениться скачком. В электрических цепях с резистивными элементами энергия электромагнитного поля не запасается, вследствие чего в них переходные процессы не возникают.

Переходные процессы в линейных электрических цепях постоянного тока 3. Математические основы анализа переходных процессов Анализ переходных процессов производят путем решения дифференциальных уравнений, составленных для исследуемой электрической цепи на основе законов Кирхгофа. При анализе переходных процессов в электрических цепях принимается, что: • рубильники включаются и размыкаются мгновенно, без возникновения электрической дуги; • время переходного процесса теоретически бесконечно • длительно, поэтому его ограничивают условным пределом – длительностью переходного процесса; • режим до коммутации – это режим, установившийся по окончании предыдущего переходного режима; • режим после коммутации рассчитывают при теоретическом условии t→∞, т. е. когда после коммутации прошло бесконечно большое время;

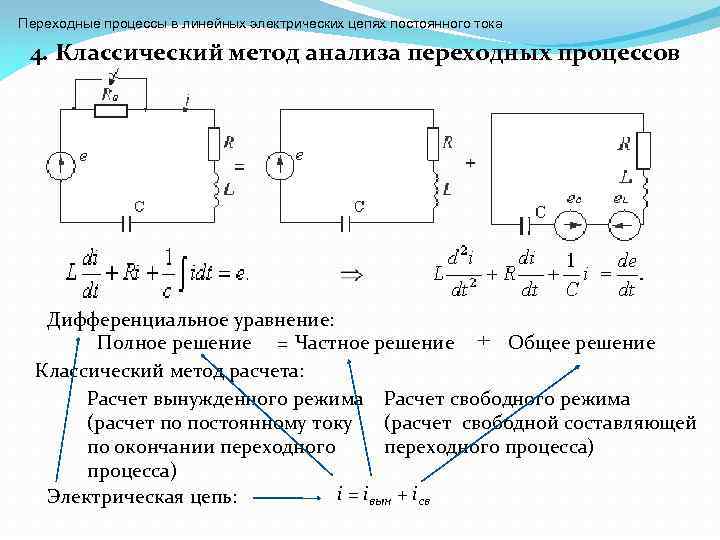Переходные процессы в линейных электрических цепях постоянного тока 4. Классический метод анализа переходных процессов Дифференциальное уравнение: Полное решение = Частное решение Общее решение Классический метод расчета: Расчет вынужденного режима Расчет свободного режима (расчет по постоянному току (расчет свободной составляющей по окончании переходного процесса) i = iвын + iсв Электрическая цепь:

Переходные процессы в линейных электрических цепях постоянного тока Решение находится в виде суммы экспонент: Для кратных корней (например, p 1 = p 2 = P) Постоянные интегрирования A 1, A 2 находят из начальных условий, определяемых на основе законов коммутации

Переходные процессы в линейных электрических цепях постоянного тока Алгоритм расчета переходного процесса классическим методом: 1. Рассчитать вынужденный (установившийся) режим при t→∞. Определить вынужденные токи и напряжения. 2. Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями. 3. Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни. 4. Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристического уравнения. 5. Переписать величины, полученные в п. 4, и производные от них при t = 0. 6. Определить необходимые зависимые начальные условия, используя независимые начальные условия. 7. Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования. 8. Записать законы изменения искомых токов и напряжений.

5. Переходные процессы в цепях первого порядка 5. 1. Переходные процессы в RC-цепях Подключение реального конденсатора к источнику постоянного напряжения (заряд конденсатора). 1. Составим систему уравнений электрического состояния: Ri + u. С = U. 2. Ищем решение этого уравнения как сумму двух слагаемых: u. С = u. Свын + u. Ссв 3. Найдем u. Свын : u. Свын =U. 4. Вычислим u. Ссв в виде: u. Ссв = А еpt.

5. Определим показатель степени р, который является корнем характеристического уравнения. Уравнение электрического состояния для свободной составляющей: После подстановки в уравнение электрического состояния получаем RCp. Aept + Aept = 0. Величина RCp +1 = 0. − τ − постоянная времени; Постоянная времени τ – это время, в течение которого свободные составляющие уменьшаются в е раз по сравнению с начальным значением τ – это величина Время t 2 − t 1 = τ , подкасательной к если любой точке экспоненты

6. Определим постоянную интегрирования А. Для начального момента времени: u. С (0+) = u. Свын (0+) + u. Ссв (0+). По второму закону коммутации u. С(0+) = u. С(0−) = 0. Свободная составляющая u. Ссв = Аерt После подстановки получим 0 =U + A. Тогда закон изменения напряжения Закон изменения тока: − по второму закону Кирхгофа − по закону Ома u. Свын (0+) = U. при t = 0+ равна А. A = −U.

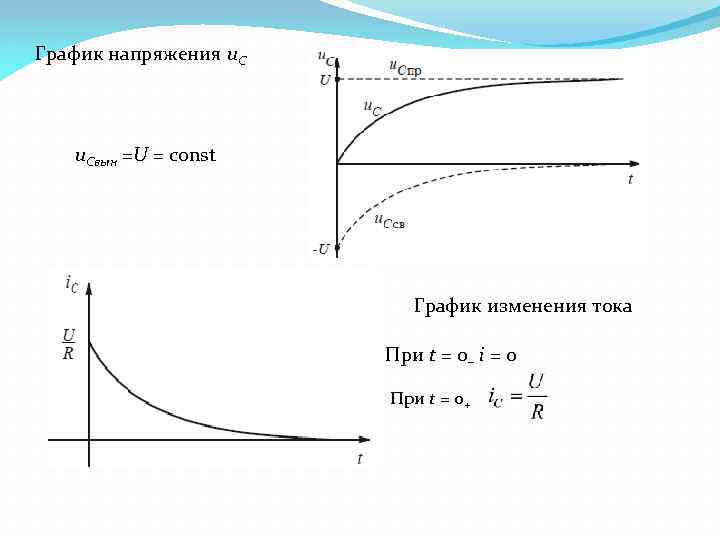График напряжения u. Свын =U = const График изменения тока При t = 0– i = 0 При t = 0+

Переходные процессы в линейных электрических цепях постоянного тока Разряд конденсатора на резистор Предварительно конденсатор заряжен до напряжения u. C(0+) = Е. Уравнение по второму закону Кирхгофа для вновь образованного контура R ∙i + u. C = 0. Дифференциальное уравнение: R i + u. C = 0 или Характеристическое уравнение RCp + 1 = 0, р = – 1/RC = – 1/τ. Общее решение для свободной составляющей u. Cсв = A ept = A e-t/τ, напряжения: А = U 0 – постоянная интегрирования; p = - 1/(RC) – корень характеристического уравнения; τ = RC – постоянная времени цепи.

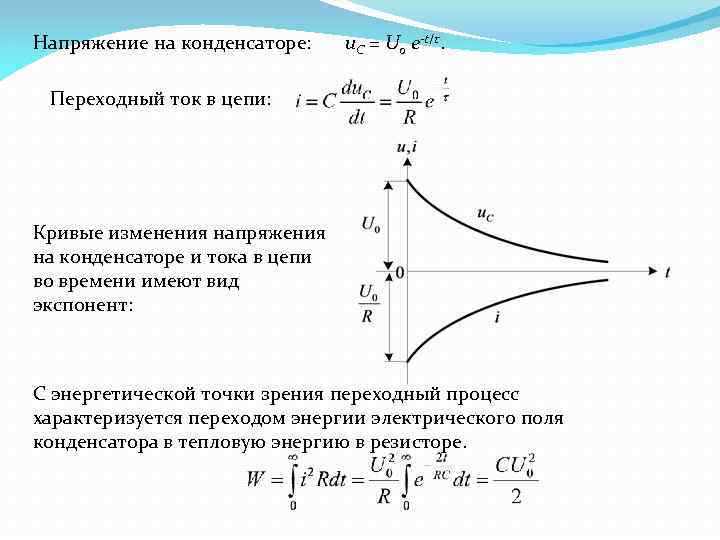Напряжение на конденсаторе: u. C = U 0 e-t/τ. Переходный ток в цепи: Кривые изменения напряжения на конденсаторе и тока в цепи во времени имеют вид экспонент: С энергетической точки зрения переходный процесс характеризуется переходом энергии электрического поля конденсатора в тепловую энергию в резисторе.

Переходные процессы в линейных электрических цепях постоянного тока Включение цепи с резистором и катушкой на постоянное напряжение i = iвын + iсв. Переходный ток в цепи 1. Установившаяся составляющая тока коммутации Iвын = U/R. 2. До коммутации ток в катушке 3. Уравнение Кирхгофа Дифференциальное уравнение Решение дифференциального уравнения i. L(0 -) = i. L(0+) = 0. u. L(t)+ u. R(t) = u(t) , p = – R/L. i. L = i. Lвын + i. Lсв. 4. Свободная составляющая тока цепи, описываемой дифференциальным уравнением первого порядка: 5. При t = 0 i = iвын + iсв = U/R + A ept=0 6. 7. 8. 0 = U/R + A; A = – U/R; iсв = – U/R · e-t/τ. после i. Lсв = A ept.

Переходные процессы в линейных электрических цепях постоянного тока Переходный ток i = U/R - U/Re-t/τ = U/R (1 - e-t/τ). Напряжение на резисторе Напряжение на катушке Скорость нарастания тока

Переходные процессы в линейных электрических цепях постоянного тока 5. 2. Переходные процессы в RL- цепях Короткое замыкание в цепи с резистором и катушкой 1. Установившийся режим в цепи до коммутации (до замыкания ключа) ) = E/(R + R). i(0 -) = i(0+ вн 2. Установившийся ток i после коммутации Iвын = 0. 3. Уравнение электрического состояния цепи после коммутации: u. L +u. R = 0 Дифференциальное уравнение: p. L + R = 0, p = – R/L, c-1 4. Общее решение уравнения для свободной составляющей: iсв = Aept 5. Общий вид переходного тока катушки: i = iвын + iсв = A ept 6. При t =0 i(0+) = i(0 -) = E/(Rвн + R) = Aept=0 Характеристическое уравнение: 7. Постоянная интегрирования A = E/(Rвн + R) = I 0. 8. Переходный ток i = iвын + iсв при этом равен

Переходные процессы в линейных электрических цепях постоянного тока Постоянная времени τ – это время, в течение которого свободная с оставляющая процесса уменьшается в е = 2, 72 раза по сравнению с начальным значением. ЭДС самоиндукции катушки Выводы: • При коротком замыкании в рассматриваемой цепи ток в ней изменяется по экспоненциальному закону, от начального значения до нуля. • Скорость изменения тока определяется постоянной времени цепи. • Практически переходный процесс заканчивается при t ≈ (3… 5)τ , когда первоначальное значение тока уменьшается по модулю на порядок. • Напряжение на катушке в начальный момент времени равно напряжению на активном сопротивлении: u. L(0+) = I 0 R. • Переходный процесс характеризуется расходом энергии магнитного поля катушки на тепловые потери в резисторе. • Сопротивление резистора влияет не на количество выделенной теплоты, а лишь на начальное значение напряжения катушки и длительность процесса.

Переходные процессы в линейных электрических цепях постоянного тока 7. Переходные процессы в цепях второго цепях (RLC-цепях) 7. 1. Разряд конденсатора на цепь с резистором и катушкой Пусть u. C(0 -) = U По второму закону Кирхгофа при t ≥ 0 Учитывая, что для свободной составляющей напряжения получаем Характеристическое уравнение Они определяют характер свободных составляющих переходных токов и напряжений.

Переходные процессы в линейных электрических цепях постоянного тока 7. 2. Апериодический разряд конденсатора на катушку и резистор Если для RLC-контура выполняется условие то напряжение на конденсаторе или u. C = u. Cсв = A 1 ∙ ep 1 t + A 2 ∙ ep 2 t, свободный ток u. Cвын = 0 Установившиеся напряжение и ток на конденсаторе Из начальных условий при t = 0 поэтому отсюда U = A 1 + A 2; i. Cвын = 0 u. C(0) = U и i(0) = 0. 0 = A 1 p 1 + A 2 p 2. A 1 = U p 2/(p 2 - p 1); A 2 = -U p 1 /(p 2 - p 1);

Переходные процессы в линейных электрических цепях постоянного тока С учетом начальных условий По теореме Виета: p 1 p 2 = 1/(LC), следовательно, ток Напряжение на катушке Апериодический разряд, при котором конденсатор все время разряжается, т. е. функция u. C(t) - убывающая, а ток i не меняет своего направления

Переходные процессы в линейных электрических цепях постоянного тока Выводы: Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения. При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение. Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля.

Переходные процессы в линейных электрических цепях постоянного тока 7. 3. Предельный апериодический разряд конденсатора на катушку и резистор При имеет место В этом случае u. C = (A 1 + A 2 t) ept; С учетом начальных условий находим: p 1 = p 2 = p = -R/(2 L). u. C(0) = U; i(0) = 0 А 1 = U; A 2 = -p U. u. C = U (1 - pt) ept; и получаем решения:

Переходные процессы в линейных электрических цепях постоянного тока 7. 4. Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкой При корни характеристического p 1, 2 = -α ± jω0 уравнения комплексные сопряженные: α = R/(2 L) – коэффициент затухания свободной составляющей; – угловая частота собственных колебаний контура; Поскольку то можно ввести обозначения

Переходные процессы в линейных электрических цепях постоянного тока Свободная составляющая переходного напряжения Свободная составляющая тока u. Cсв = A e-αt sin(ω0 t + ψ) iсв = C A e-αt (-α sin(ω0 t + ψ) + ω0 cos(ω0 t + ψ)). С учетом начальных условий при t = 0 u. C = U 0 , i = 0 U 0 = A sin ψ; 0 = C A (-α sin ψ + ω0 cosψ). откуда Переходные напряжения и ток: u. C = UCm e-αt sin(ω0 t + ψ); i = -Im e-αt sin(ω0 t + π); u. L= ULm e-αt sin(ω0 t - ψ),

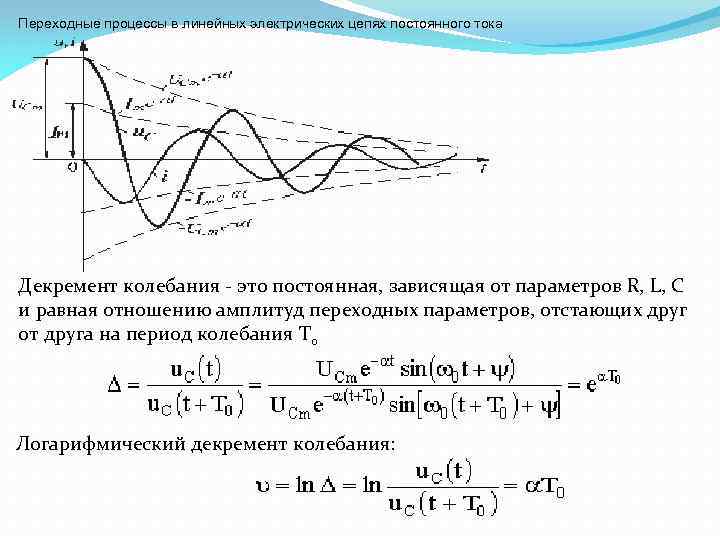Переходные процессы в линейных электрических цепях постоянного тока Декремент колебания - это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т 0 Логарифмический декремент колебания:

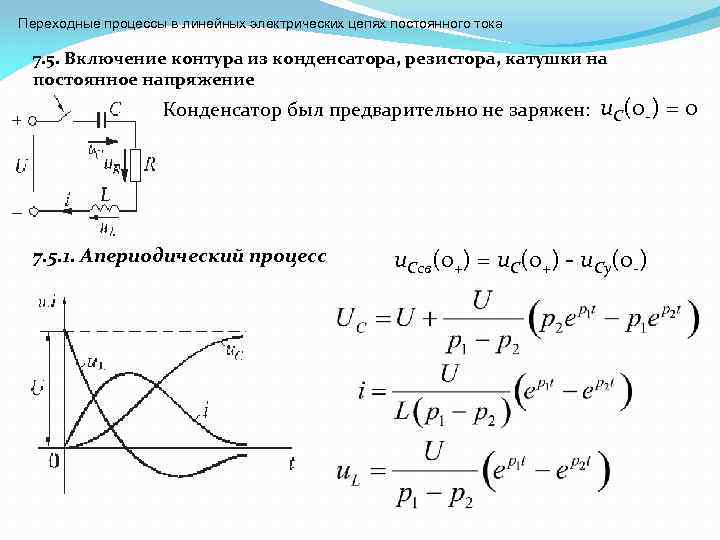Переходные процессы в линейных электрических цепях постоянного тока 7. 5. Включение контура из конденсатора, резистора, катушки на постоянное напряжение Конденсатор был предварительно не заряжен: 7. 5. 1. Апериодический процесс u. C(0 -) = 0 u. Cсв(0+) = u. C(0+) - u. Cу(0 -)

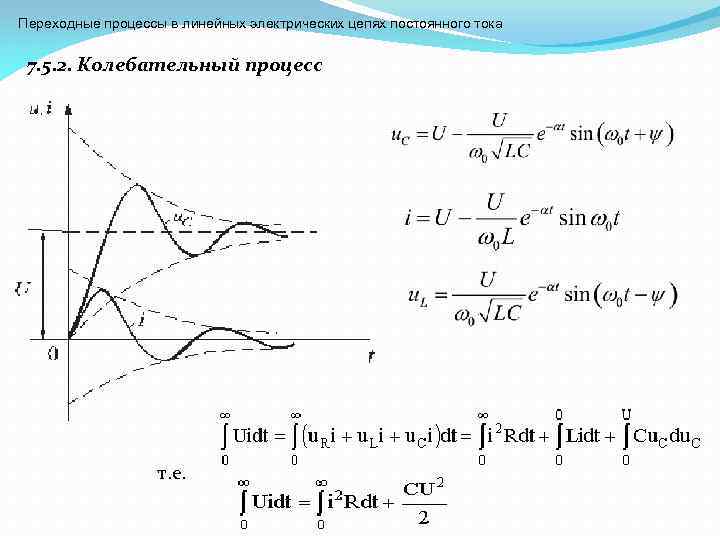Переходные процессы в линейных электрических цепях постоянного тока 7. 5. 2. Колебательный процесс т. е.

Анализ переходных процессов в пространстве состояний