Основные уравнения движения газа используемые при математическом описании

Основные уравнения движения газа, используемые при математическом описании процессов в двигателях и их элементах. ЛЕКЦИЯ 2 Уравнения: -НЕРАЗРЫВНОСТИ-СОХРАНЕНИЯ ЭНЕРГИИ-УРАВНЕНИЕ БЕРНУЛЛИ-

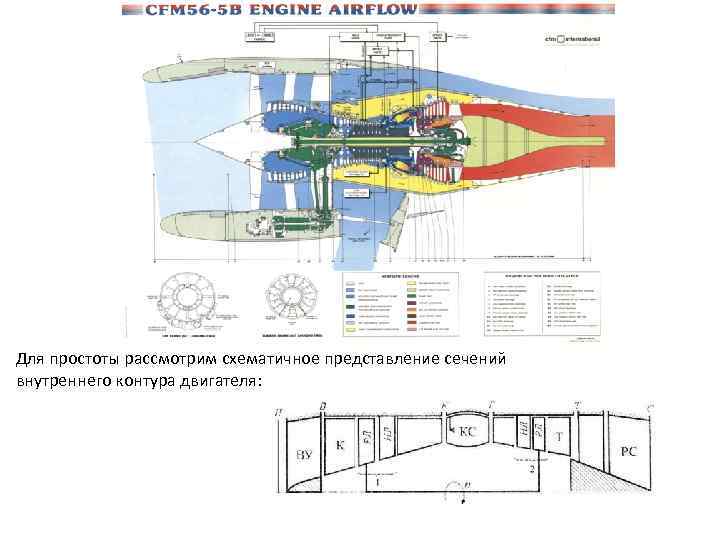Для простоты рассмотрим схематичное представление сечений внутреннего контура двигателя:

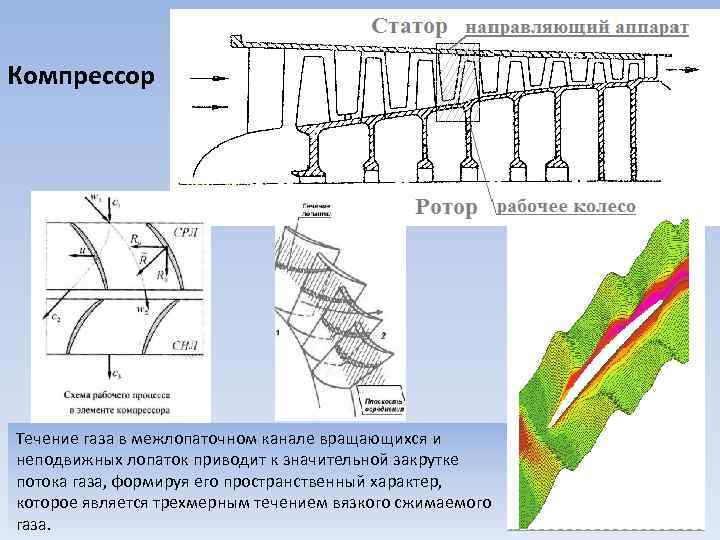Компрессор Течение газа в межлопаточном канале вращающихся и неподвижных лопаток приводит к значительной закрутке потока газа, формируя его пространственный характер, которое является трехмерным течением вязкого сжимаемого газа.

Допущения, принимаемые при математическом описании процессов в лопаточных машинах. Уравнения, связывающие параметры газового потока в различных сечениях двигателя, для описания пространственного неустановившегося течения вязкого газа весьма сложны для инженерных расчетов. Поэтому для практического анализа рабочих процессов используют уравнения, построенные при определенных допущениях: • • Движение газа считается установившимся. Поток считается одномерным. Действие массовых сил не учитывается. Параметры газа в поперечном сечении равны их средним значениям.

Уравнение неразрывности • Рассматриваются жидкости, обладающие свойством сплошности, которое предполагает непрерывность изменения параметров потока и их производных в пространстве и времени. Уравнение неразрывности формулируется следующим образом: массовый расход жидкости вдоль трубки тока остается постоянным. Рассматривается струя идеальной жидкости, протекающей со скоростями v 1 и v 2 через сечения S 1 и S 2. Т. к. жидкость неразрывна, то через сечения S 1 и S 2 за время Δt пройдут одинаковые секундные массы Δm жидкости: S 2 v 2 ρ2= S 1 v 1 ρ1= const - уравнение неразрывности струи.

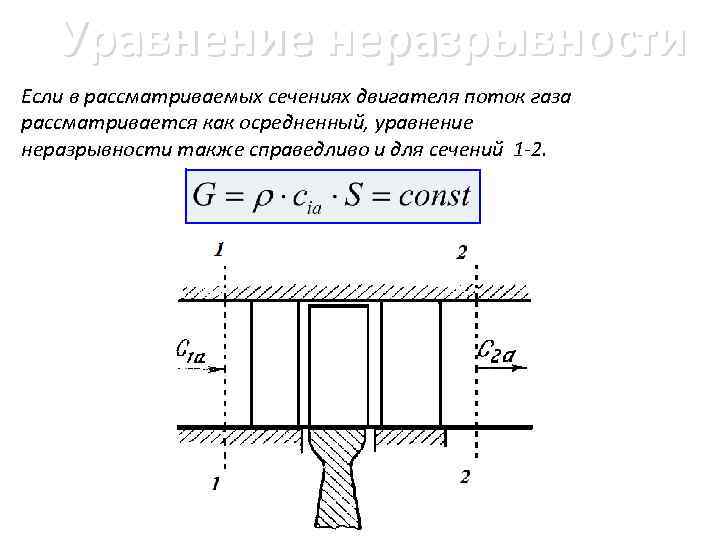Уравнение неразрывности Если в рассматриваемых сечениях двигателя поток газа рассматривается как осредненный, уравнение неразрывности также справедливо и для сечений 1 -2.

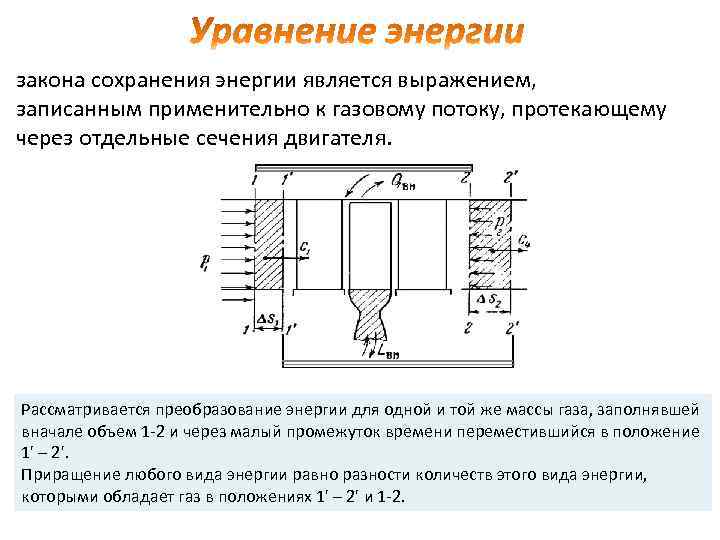закона сохранения энергии является выражением, записанным применительно к газовому потоку, протекающему через отдельные сечения двигателя. Рассматривается преобразование энергии для одной и той же массы газа, заполнявшей вначале объем 1 -2 и через малый промежуток времени переместившийся в положение 1' – 2'. Приращение любого вида энергии равно разности количеств этого вида энергии, которыми обладает газ в положениях 1' – 2' и 1 -2.

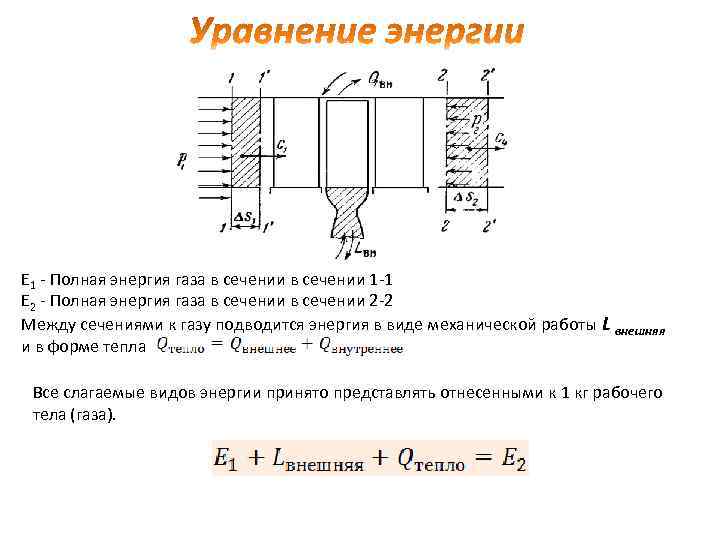E 1 - Полная энергия газа в сечении 1 -1 E 2 - Полная энергия газа в сечении 2 -2 Между сечениями к газу подводится энергия в виде механической работы L внешняя и в форме тепла Все слагаемые видов энергии принято представлять отнесенными к 1 кг рабочего тела (газа).

Виды энергий для объемов (слагаемые энергии E): • Кинетическая Энергия • Потенциальная Энергия: энергия давления и энергия положения • Внутренняя Энергия • Энергия тепла за счет трения Энергией положения для произвольных сечений двигателя пренебрегают в виду ее малости.

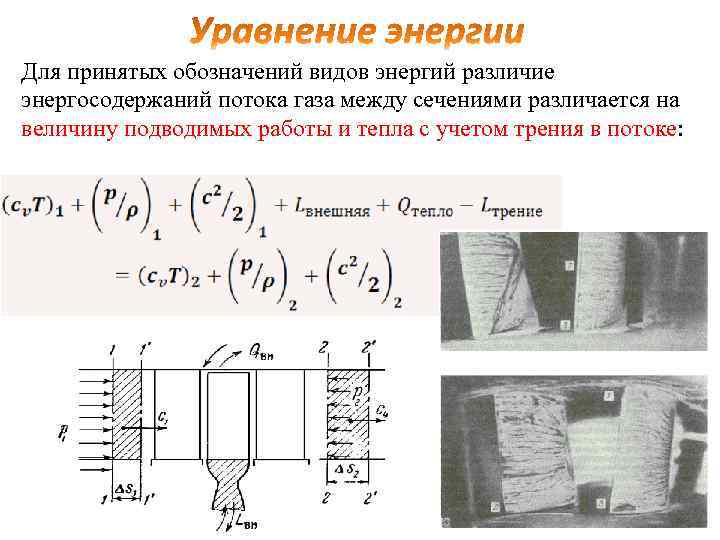Для принятых обозначений видов энергий различие энергосодержаний потока газа между сечениями различается на величину подводимых работы и тепла с учетом трения в потоке:

Дифференциальная форма: + d. L – изменение работы компрессора - d. L – изменение работы турбины

С учетом того, что Из курса термодинамики известно соотношение, которое с учетом уравнения состояния идеального газа имеет вид - энтальпия газа или полное энергосодержание газа Для сечений двигателя между которыми отсутствует подвод механической энергии и тепла уравнение энергии показывает, что сумма энтальпии и кинетической энергии сохраняется неизменной. - полное теплосодержание Энтальпия заторможенного потока при отсутствии подвода (отвода) механической энергии и внешнего тепла для двух сечений, между которыми рассматривается газодинамический процесс, есть величина постоянная.

Для компрессора при отсутствии теплообмена с внешней средой имеем Работа совершаемая компрессором идет на увеличение полной энтальпии потока газа в компрессоре Для турбины при отсутствии теплообмена с внешней средой имеем уменьшение полной энтальпии потока газа в турбине идет на создание механической работы турбины Для камеры сгорания тепло сгоревшего топлива в камере сгорания идет на увеличение полной энтальпии потока газа

Выражения параметров потока через число Маха Разделим обе части равенства на теплосодержание умножим и разделим левую часть выражения на газовую постоянную R принимаем во внимание, что Число звука

Выражения параметров потока через число Маха Если определить, что изменение давления торможения подчиняется соотношению идеальной адиабаты можно записать Число Маха является критерием подобия для течений газа

Выражения параметров потока через число Маха критический режим течения, которому соответствует критическая температура Скорость звука критического режима приведенная скорость потока Связь между числом Маха и приведенной скоростью дается выражением

• Рассмотрено уравнение теплосодержания, дающее связь температуры газа со скоростью его движения с учетом подвода тепла и технической работы. Такие параметры как давление и плотность в уравнение теплосодержания не входили. Можно получить механическую форму уравнения энергии, в котором скорость газа связана только с его давлением и плотностью.

Уравнение энергии в дифференциальной форме имеет вид (1) Из первого закона термодинамики для элементарного объема газа тепло, подведенное к рассматриваемому объему, идет на изменение внутренней энергии d. U и на совершение работы pdv по преодолению сил давления, связанной с изменением объема газа. (2) Вычитая из (1) уравнение (2) Или поскольку имеем уравнение Бернулли - для турбины с учетом

• Смысл уравнения Бернулли: Внешняя механическая работа, подводимая в компрессоре к потоку газа расходуется на: - совершение работы сжатия, - изменение кинетической энергии газа - преодоление гидравлических сопротивлений. Работа, совершаемая газом при его расширении в турбине, расходуется на: - создание механической работы - увеличение кинетической энергии потока - преодоление гидравлических потерь.

Работа компрессора и турбины Поскольку запишем В процессе движения выделенного элементарного объема газа имеет место его деформация, в p-v обозначенная линией 1 -2 поэтому

Работа компрессора и турбины Ранее было сказано, что Изменение теплосодержания Работа сил сжатия Изменение состояния газа при его течении с трением и теплообменом характеризуют уравнением политропы

Работа компрессора и турбины компрессор турбина политропическая работа сжатия политропическая работа расширения

Работа компрессора и турбины Учет скоростей потока в проточной части Средняя скорость потока газа: - на входе в компрессор достигает значений ~ 200 -250 м/с -на выходе компрессора снижается до 80 -130 м/с - на входе в турбину ~ 100 м/c -- на выходе из турбины увеличивается ~ 300 м/с Изменение кинетической энергии потока в компрессоре в среднем достигает уровня Изменение кинетической энергии потока в турбине в среднем достигает уровня При суммарной величине работы ~ 300000 ~ 400000 Дж/кг поправка к величине работы компрессора составляет 3%~10%

Работа компрессора и турбины Пренебрегая работой трения, представим уравнение Бернулли выражение технической работы через полные параметры компрессор степень сжатия компрессора турбина степень расширения турбины