Основные принципы обработки полученных данных Данные Свойства






















































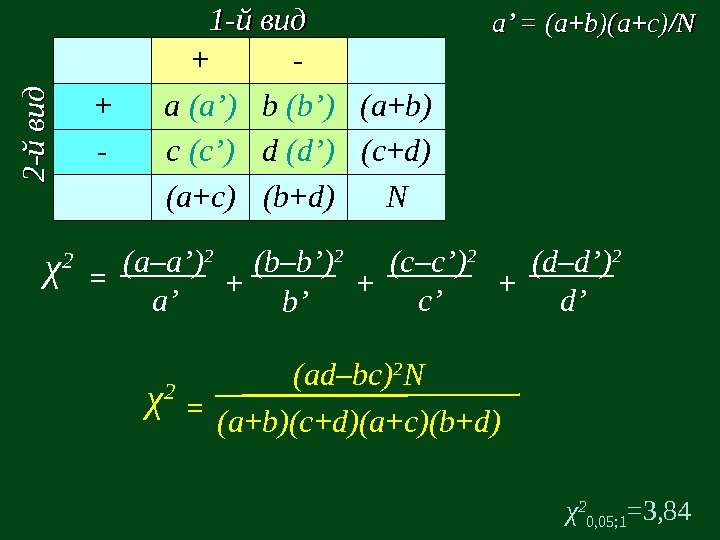










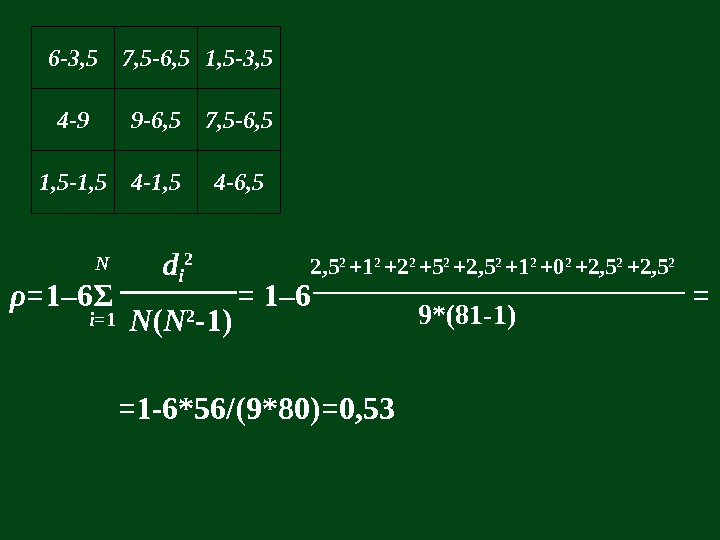

andat2011-1-4.ppt
- Размер: 7.6 Мб
- Автор:
- Количество слайдов: 111
Описание презентации Основные принципы обработки полученных данных Данные Свойства по слайдам
 Основные принципы обработки полученных данных
Основные принципы обработки полученных данных
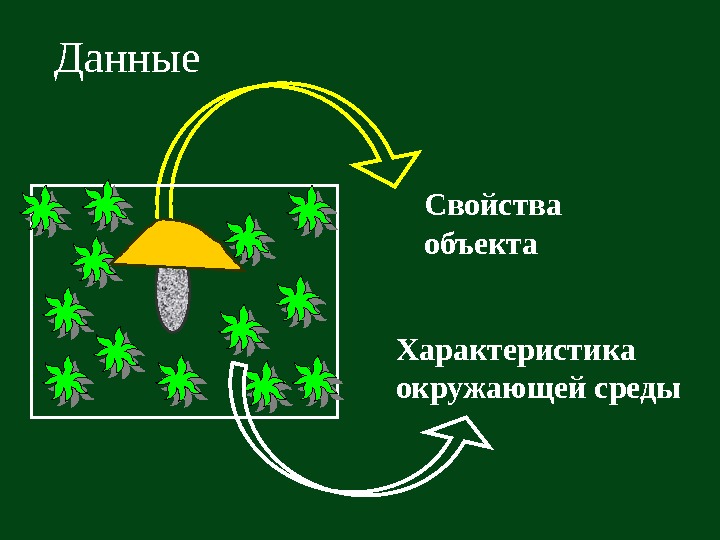
 Данные Свойства объекта Характеристика окружающей среды
Данные Свойства объекта Характеристика окружающей среды
 Количественные данные Дискретные Непрерывные Число плодовых тел, шт Сухой вес мицелия, мг Размер спор, мкм Число КОЕ в 1 г почвы, шт Концентрация спор в суспензии, шт/мл Температура, 0 С р. Н
Количественные данные Дискретные Непрерывные Число плодовых тел, шт Сухой вес мицелия, мг Размер спор, мкм Число КОЕ в 1 г почвы, шт Концентрация спор в суспензии, шт/мл Температура, 0 С р. Н
 Порядковые данные Размерная категория валежа; Степень разложения древесины; Влажность почвы (сухая-свежая-влажноватая-влажная-сырая); Развитие болезни.
Порядковые данные Размерная категория валежа; Степень разложения древесины; Влажность почвы (сухая-свежая-влажноватая-влажная-сырая); Развитие болезни.
 Порядковые данные Баллы развития болезни 0 Растение здоровое. 1 Слабое поражение органа или растения. 2 Поражение среднее, сильно пораженные органы не встречаются. 3 Поражение среднее, некоторые органы или растения поражены в сильной степени. 4 Сильное поражение органов или растений, их гибель.
Порядковые данные Баллы развития болезни 0 Растение здоровое. 1 Слабое поражение органа или растения. 2 Поражение среднее, сильно пораженные органы не встречаются. 3 Поражение среднее, некоторые органы или растения поражены в сильной степени. 4 Сильное поражение органов или растений, их гибель.
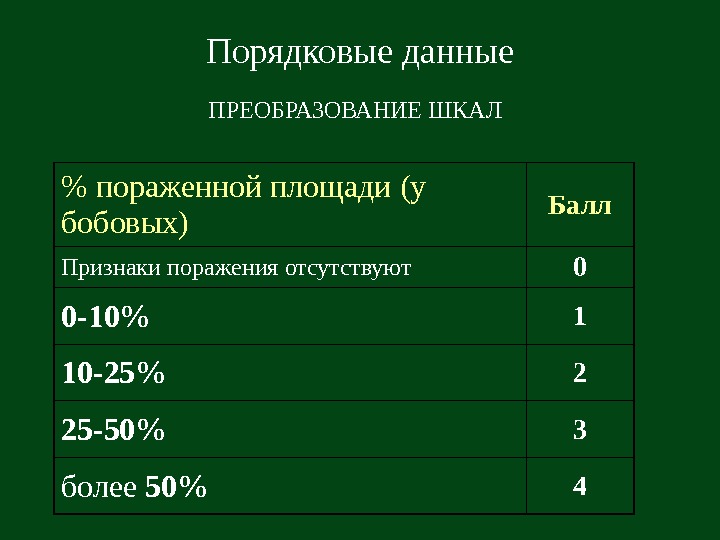
 Порядковые данные ПРЕОБРАЗОВАНИЕ ШКАЛ % пораженной площади (у бобовых) Балл Признаки поражения отсутствуют 0 0 -10% 1 10 -25% 2 25 -50% 3 более 50%
Порядковые данные ПРЕОБРАЗОВАНИЕ ШКАЛ % пораженной площади (у бобовых) Балл Признаки поражения отсутствуют 0 0 -10% 1 10 -25% 2 25 -50% 3 более 50%
 Порядковые данные Количественные данные всегда можно перевести в порядковые. Часть информации при этом потеряется.
Порядковые данные Количественные данные всегда можно перевести в порядковые. Часть информации при этом потеряется.
 Качественные данные Видовые списки Acremonium kiliense Grütz Acremonium strictum W. Gams Apiospora montagnei Sacc. Aspergillus fumigatus Fresen. Aspergillus wentii Wehmer Cladosporium herbarum (Pers. ) Link Clonostachys rosea (Preuss) Mussat Coniothyrium fuckeli Sacc. Fusarium sambucinum Fuckel Geomyces pannorum (Link) Sigler et J. W. Carmich. Humicola grisea Traaen Mucor hiemalis Wehmer Penicillium janczewskii K. M. Zalessky Trichoderma hamatum (Bonord. ) Bainier
Качественные данные Видовые списки Acremonium kiliense Grütz Acremonium strictum W. Gams Apiospora montagnei Sacc. Aspergillus fumigatus Fresen. Aspergillus wentii Wehmer Cladosporium herbarum (Pers. ) Link Clonostachys rosea (Preuss) Mussat Coniothyrium fuckeli Sacc. Fusarium sambucinum Fuckel Geomyces pannorum (Link) Sigler et J. W. Carmich. Humicola grisea Traaen Mucor hiemalis Wehmer Penicillium janczewskii K. M. Zalessky Trichoderma hamatum (Bonord. ) Bainier
 Качественные данные Список видов может относиться к различным элементам опробования: территория; совокупность однородных объектов; отдельный образец (воды, почвы и т. п. )
Качественные данные Список видов может относиться к различным элементам опробования: территория; совокупность однородных объектов; отдельный образец (воды, почвы и т. п. )
 Качественные данные Субстрат/организм-хозяин Лишайники Почва, основание стволов деревьев, замшелые субстраты, кора деревьев (различных пород), камни (различных пород), антропогенные субстраты. Трутовые грибы Лиственное или хвойное дерево; живое дерево или отмершая древесина. Фитопатоген ные грибы Вид растения-хозяина
Качественные данные Субстрат/организм-хозяин Лишайники Почва, основание стволов деревьев, замшелые субстраты, кора деревьев (различных пород), камни (различных пород), антропогенные субстраты. Трутовые грибы Лиственное или хвойное дерево; живое дерево или отмершая древесина. Фитопатоген ные грибы Вид растения-хозяина
 Качественные данные Сыроежки (шляпка) Охристая, охристо-буроватая, фиолетово-лиловая, лиловатая, синеватая, синяя, сине-лиловая, черно-лиловая, черно-оливковая, бордово-красная, розовато-пурпрная и т. д. Трутовые грибы (ткань) Белая, желтоватая, буро-глинистая, оранжево-рыжая, рыже-ржавая, красновато-бурая, винно-розовая, коричневатая, цвета какао и т. д. Цветовые шкалы
Качественные данные Сыроежки (шляпка) Охристая, охристо-буроватая, фиолетово-лиловая, лиловатая, синеватая, синяя, сине-лиловая, черно-лиловая, черно-оливковая, бордово-красная, розовато-пурпрная и т. д. Трутовые грибы (ткань) Белая, желтоватая, буро-глинистая, оранжево-рыжая, рыже-ржавая, красновато-бурая, винно-розовая, коричневатая, цвета какао и т. д. Цветовые шкалы
 Качественные данные Агариковые грибы Запах приятный или неприятный, запах чеснока, запах муки, запах карболки и т. д. ; вкус горький, едкий, жгуче-перечный, сладковатый, кисловато-вяжущий и т. д. Запах и вкус
Качественные данные Агариковые грибы Запах приятный или неприятный, запах чеснока, запах муки, запах карболки и т. д. ; вкус горький, едкий, жгуче-перечный, сладковатый, кисловато-вяжущий и т. д. Запах и вкус
 Качественные данные Текстовая характеристика исследуемых объектов на основе предварительных анализов. Плазмодиокарпы сидячие или на тонких ножках, свисающие, простые или ветвящиеся, уплощенные или вальковатые, образующие объемную сеть, желтые или оливковые. Перидий однослойный, пленчатый, светло-желтый, инкрустирован маленькими скоплениями желтой или охряной извести. Ножка нитевидная, является непосредственным продолжением гипоталлуса, желтая. Капиллиций эластичный, состоит из бесцветных трубочек, иногда образующих в местах ветвления маленькие желтые узелки. Споры в массе черные. Erionema aureum Penzig. Стр. 196. Новожилов Ю. К. Класс Миксомицеты, 1993.
Качественные данные Текстовая характеристика исследуемых объектов на основе предварительных анализов. Плазмодиокарпы сидячие или на тонких ножках, свисающие, простые или ветвящиеся, уплощенные или вальковатые, образующие объемную сеть, желтые или оливковые. Перидий однослойный, пленчатый, светло-желтый, инкрустирован маленькими скоплениями желтой или охряной извести. Ножка нитевидная, является непосредственным продолжением гипоталлуса, желтая. Капиллиций эластичный, состоит из бесцветных трубочек, иногда образующих в местах ветвления маленькие желтые узелки. Споры в массе черные. Erionema aureum Penzig. Стр. 196. Новожилов Ю. К. Класс Миксомицеты, 1993.
 Качественные данные Текстовая характеристика исследуемых объектов на основе предварительных анализов. Грибы по группам съедобности Выделение групп 1 Самые вкусные и ценные виды, дающие лучшую грибную продукцию. Белый гриб 2 Виды хорошие и довольно ценные, но уже значительно уступающие предыдущим. Березовик обыкновенный 3 Виды по вкусу и ценности характеризуемые – «так себе» . Валуй 4 Сравнительно плохие грибы. Строчок
Качественные данные Текстовая характеристика исследуемых объектов на основе предварительных анализов. Грибы по группам съедобности Выделение групп 1 Самые вкусные и ценные виды, дающие лучшую грибную продукцию. Белый гриб 2 Виды хорошие и довольно ценные, но уже значительно уступающие предыдущим. Березовик обыкновенный 3 Виды по вкусу и ценности характеризуемые – «так себе» . Валуй 4 Сравнительно плохие грибы. Строчок
 Качественные данные Альтернативные данные Вид на данной территории присутствует – вид на данной территории отсутствует Растение больное – растение здоровое “ +” “–”
Качественные данные Альтернативные данные Вид на данной территории присутствует – вид на данной территории отсутствует Растение больное – растение здоровое “ +” “–”
 Качественные данные Альтернативные данные + 1 – 0 Формальное преобразование качественной альтернативной шкалы в количественную служит для проведения ряда вычислений. Но данные сохраняют качественный характер!
Качественные данные Альтернативные данные + 1 – 0 Формальное преобразование качественной альтернативной шкалы в количественную служит для проведения ряда вычислений. Но данные сохраняют качественный характер!
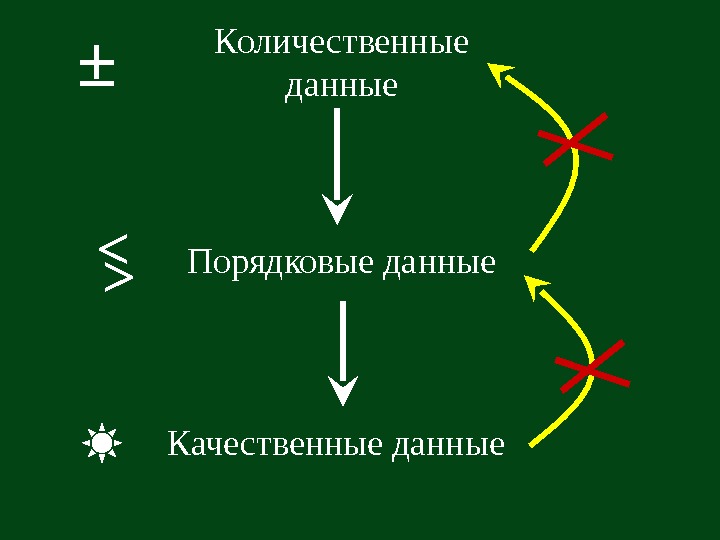
 Количественные данные Порядковые данные Качественные данные±
Количественные данные Порядковые данные Качественные данные±
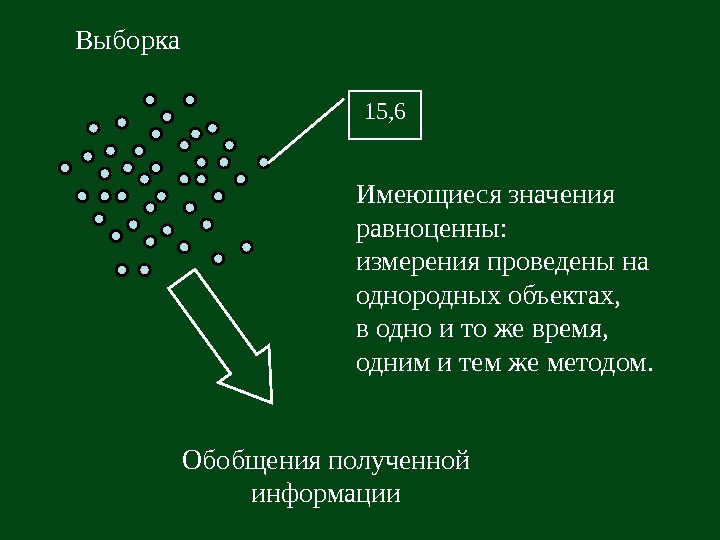
 15, 6 Выборка Имеющиеся значения равноценны: измерения проведены на однородных объектах, в одно и то же время, одним и тем же методом. Обобщения полученной информации
15, 6 Выборка Имеющиеся значения равноценны: измерения проведены на однородных объектах, в одно и то же время, одним и тем же методом. Обобщения полученной информации
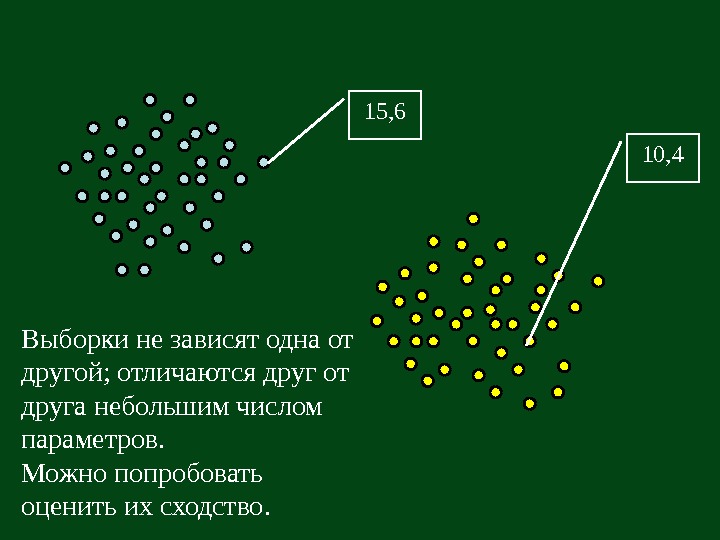
 15, 6 10, 4 Выборки не зависят одна от другой; отличаются друг от друга небольшим числом параметров. Можно попробовать оценить их сходство.
15, 6 10, 4 Выборки не зависят одна от другой; отличаются друг от друга небольшим числом параметров. Можно попробовать оценить их сходство.
 Попарно связанные данные
Попарно связанные данные
 Попарно связанные данные Пример: Масса заготовленных плодовых тел съедобных грибов с разных областей – по годам.
Попарно связанные данные Пример: Масса заготовленных плодовых тел съедобных грибов с разных областей – по годам.
 Попарно связанные данные
Попарно связанные данные
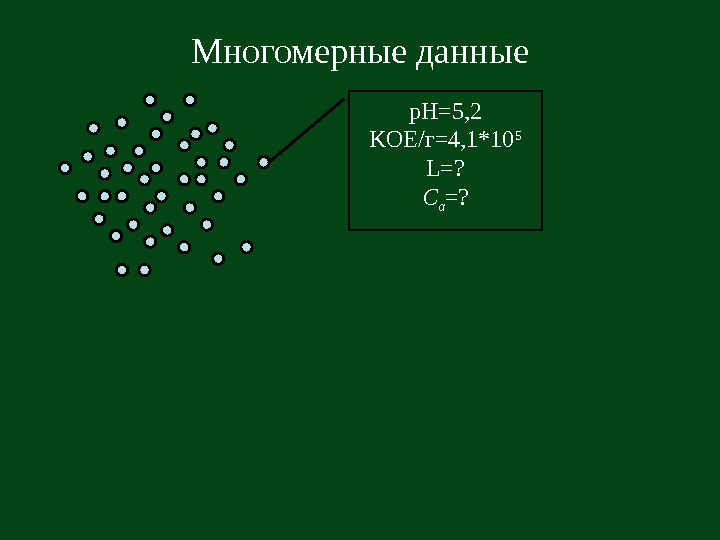
 p. H=5, 2 KOE/ г = 4, 1*10 5 L=? C α =? Многомерные данные
p. H=5, 2 KOE/ г = 4, 1*10 5 L=? C α =? Многомерные данные
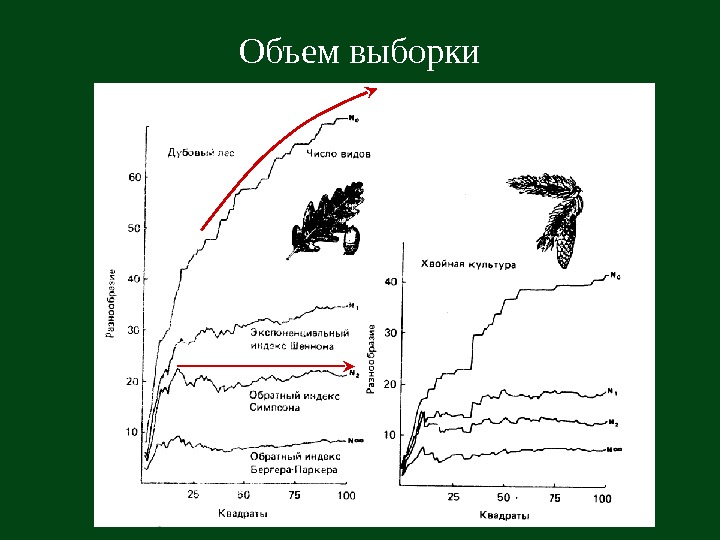
 Объем выборки На практике большинство исследователей поступают прагматически и собирают столько материала, сколько позволяют им время или деньги, или же пока интуиция не подсказывает им, что данных для адекватного описания разнообразия достаточно. Э. Мэгарран, 1992. Экологическое разнообразие и его измерение.
Объем выборки На практике большинство исследователей поступают прагматически и собирают столько материала, сколько позволяют им время или деньги, или же пока интуиция не подсказывает им, что данных для адекватного описания разнообразия достаточно. Э. Мэгарран, 1992. Экологическое разнообразие и его измерение.
 Объем выборки
Объем выборки
 С какой повторностью работать? Можно работать с любой повторностью. Выбор повторности зависит от целей исследования и обобщений, которые вы надеетесь сделать.
С какой повторностью работать? Можно работать с любой повторностью. Выбор повторности зависит от целей исследования и обобщений, которые вы надеетесь сделать.
 Измерение диаметра одной и той же колонии в разное время даст информацию о росте данной конкретной колонии (клона). (Скорее всего, повтор этого опыта с тем же клоном покажет несколько иные результаты…) Измерение диаметра колоний нескольких клонов одного штамма даст информацию о росте данного штамма. Использование нескольких штаммов , возможно, позволит сказать что-то о виде в целом.
Измерение диаметра одной и той же колонии в разное время даст информацию о росте данной конкретной колонии (клона). (Скорее всего, повтор этого опыта с тем же клоном покажет несколько иные результаты…) Измерение диаметра колоний нескольких клонов одного штамма даст информацию о росте данного штамма. Использование нескольких штаммов , возможно, позволит сказать что-то о виде в целом.
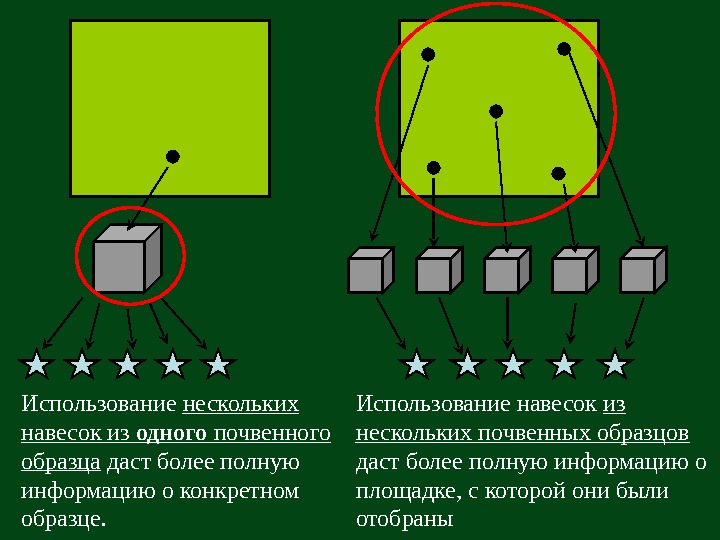
 Использование нескольких навесок из одного почвенного образца даст более полную информацию о конкретном образце. Использование навесок из нескольких почвенных образцов даст более полную информацию о площадке, с которой они были отобраны
Использование нескольких навесок из одного почвенного образца даст более полную информацию о конкретном образце. Использование навесок из нескольких почвенных образцов даст более полную информацию о площадке, с которой они были отобраны
 Повторность 1. Повтор во времени – временн á я повторность. Служит для компенсации случайных изменений условий , происходящих во времени. Необходимо проводить в один и тот же сезон (сезонные изменения – неслучайны!). 2. Повтор во пространстве – пространственная повторность (закладка нескольких площадок, взятие нескольких почвенных образцов и т. п. ). Служит для компенсации пространственной неоднородности. 3. Повтор по объектам (использование нескольких штаммов и т. п. ). Служит для компенсации фенотипической изменчивости различных организмов.
Повторность 1. Повтор во времени – временн á я повторность. Служит для компенсации случайных изменений условий , происходящих во времени. Необходимо проводить в один и тот же сезон (сезонные изменения – неслучайны!). 2. Повтор во пространстве – пространственная повторность (закладка нескольких площадок, взятие нескольких почвенных образцов и т. п. ). Служит для компенсации пространственной неоднородности. 3. Повтор по объектам (использование нескольких штаммов и т. п. ). Служит для компенсации фенотипической изменчивости различных организмов.
 Некоторые схемы отбора проб
Некоторые схемы отбора проб
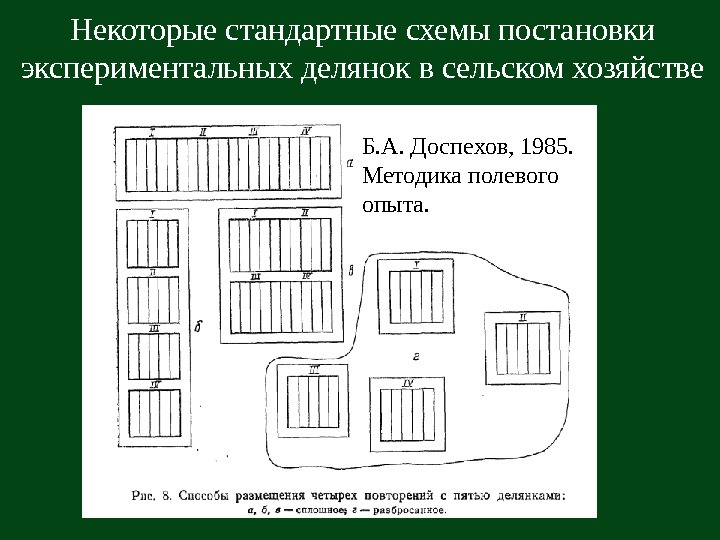
 Некоторые стандартные схемы постановки экспериментальных делянок в сельском хозяйстве Б. А. Доспехов, 1985. Методика полевого опыта.
Некоторые стандартные схемы постановки экспериментальных делянок в сельском хозяйстве Б. А. Доспехов, 1985. Методика полевого опыта.
 Точность измерения 1. Точность прибора обычно составляет полделения шкалы (например, для обычной линейки, точность измерения – 0, 5 мм). Измерение не может быть проведено с точностью превышающей точность измерительного прибора! 2. При большом разбросе значений нет смысла проводить измерение с высокой точностью.
Точность измерения 1. Точность прибора обычно составляет полделения шкалы (например, для обычной линейки, точность измерения – 0, 5 мм). Измерение не может быть проведено с точностью превышающей точность измерительного прибора! 2. При большом разбросе значений нет смысла проводить измерение с высокой точностью.
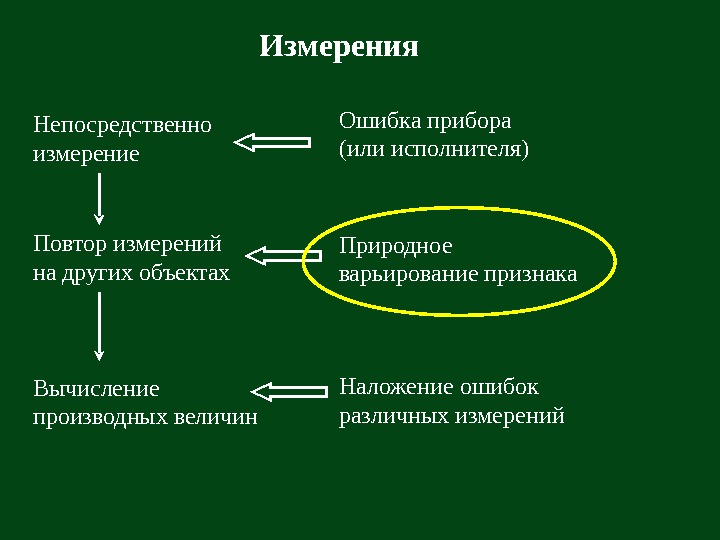
 Непосредственно измерение Измерения Ошибка прибора (или исполнителя) Повтор измерений на других объектах Природное варьирование признака Вычисление производных величин Наложение ошибок различных измерений
Непосредственно измерение Измерения Ошибка прибора (или исполнителя) Повтор измерений на других объектах Природное варьирование признака Вычисление производных величин Наложение ошибок различных измерений
 Бессмысленно проводить измерения, если погрешность прибора существенно превышает природное варьирование признака!
Бессмысленно проводить измерения, если погрешность прибора существенно превышает природное варьирование признака!
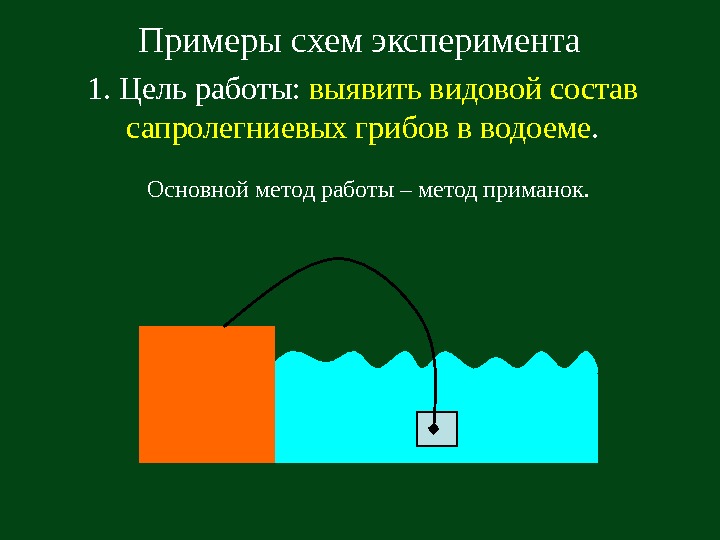
 Примеры схем эксперимента 1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме. Основной метод работы – метод приманок.
Примеры схем эксперимента 1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме. Основной метод работы – метод приманок.
 Примеры схем эксперимента 1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме. Что необходимо учесть? 1) Можно ставить приманки непосредственно в водоеме или брать пробы воды и работать с ними в лаборатории. 2) Водоем имеет площадь и глубину. 3) Возможно, существует сезонная динамика развития сапролегниевых грибов. 4) Разные виды имеют разные оптимумы температур. 5) Существуют различные типы приманок.
Примеры схем эксперимента 1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме. Что необходимо учесть? 1) Можно ставить приманки непосредственно в водоеме или брать пробы воды и работать с ними в лаборатории. 2) Водоем имеет площадь и глубину. 3) Возможно, существует сезонная динамика развития сапролегниевых грибов. 4) Разные виды имеют разные оптимумы температур. 5) Существуют различные типы приманок.
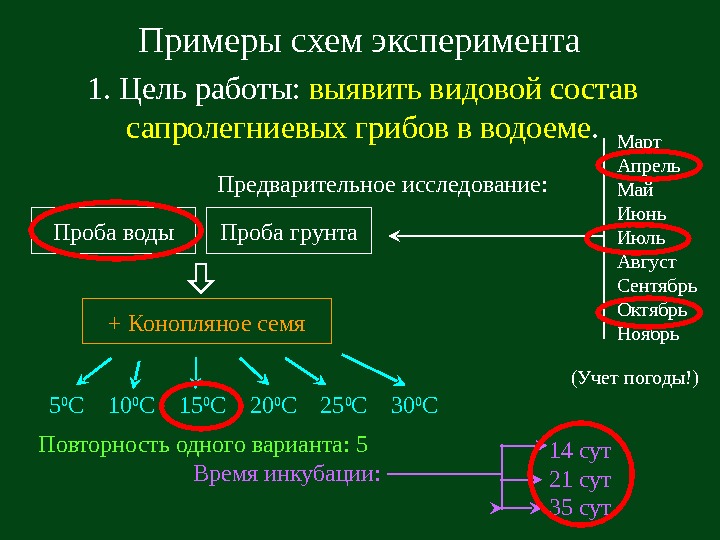
 Примеры схем эксперимента 1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме. Предварительное исследование: Проба воды Проба грунта Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь+ Конопляное семя 5 0 С 10 0 С 15 0 С 20 0 С 25 0 С 30 0 С Повторность одного варианта: 5 Время инкубации: 14 сут 21 сут 35 сут (Учет погоды!)
Примеры схем эксперимента 1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме. Предварительное исследование: Проба воды Проба грунта Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь+ Конопляное семя 5 0 С 10 0 С 15 0 С 20 0 С 25 0 С 30 0 С Повторность одного варианта: 5 Время инкубации: 14 сут 21 сут 35 сут (Учет погоды!)
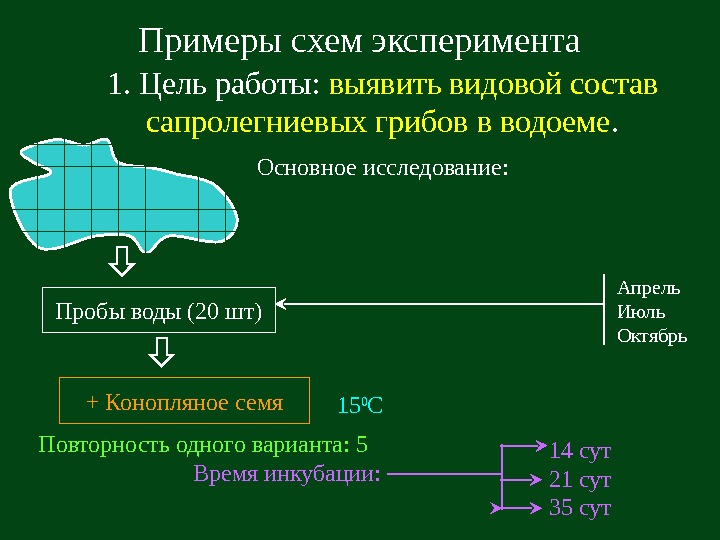
 Примеры схем эксперимента Основное исследование: Пробы воды (20 шт) Апрель Июль Октябрь + Конопляное семя 15 0 С Повторность одного варианта: 5 Время инкубации: 14 сут 21 сут 35 сут1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме.
Примеры схем эксперимента Основное исследование: Пробы воды (20 шт) Апрель Июль Октябрь + Конопляное семя 15 0 С Повторность одного варианта: 5 Время инкубации: 14 сут 21 сут 35 сут1. Цель работы: выявить видовой состав сапролегниевых грибов в водоеме.
 Примеры схем эксперимента 2. Цель работы: проверить, влияет ли температура воды на развитие сапролегниевых грибов в водоеме; и если влияет – то как? Что необходимо учесть? 1) Можно работать только методом приманок непосредственно в водоеме. 2) Водоем имеет площадь. 3) Температура воды в течение суток принимает разные значения. 4) Вероятно, влияние оказывает как текущая температура воды, так и температурный режим в течение предшествующих дней. 5) Понятие «развития грибов» может включать как видовое богатство, так и интенсивность обрастания приманок.
Примеры схем эксперимента 2. Цель работы: проверить, влияет ли температура воды на развитие сапролегниевых грибов в водоеме; и если влияет – то как? Что необходимо учесть? 1) Можно работать только методом приманок непосредственно в водоеме. 2) Водоем имеет площадь. 3) Температура воды в течение суток принимает разные значения. 4) Вероятно, влияние оказывает как текущая температура воды, так и температурный режим в течение предшествующих дней. 5) Понятие «развития грибов» может включать как видовое богатство, так и интенсивность обрастания приманок.
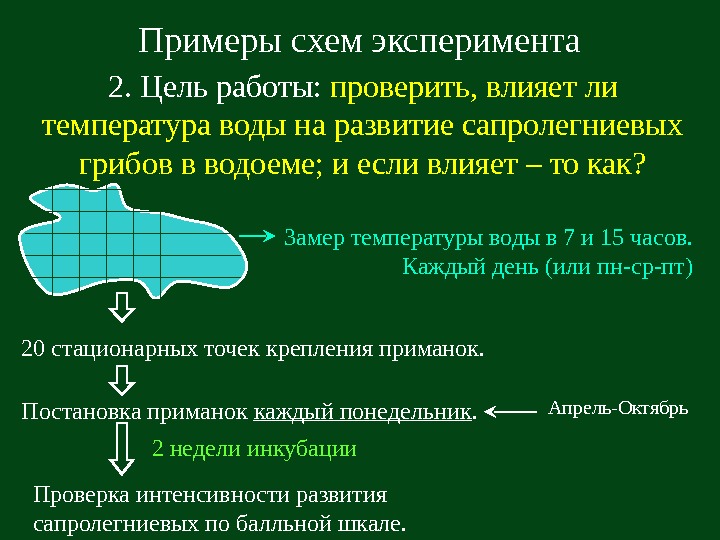
 Примеры схем эксперимента 2. Цель работы: проверить, влияет ли температура воды на развитие сапролегниевых грибов в водоеме; и если влияет – то как? Апрель-Октябрь20 стационарных точек крепления приманок. Постановка приманок каждый понедельник. Проверка интенсивности развития сапролегниевых по балльной шкале. 2 недели инкубации Замер температуры воды в 7 и 15 часов. Каждый день (или пн-ср-пт)
Примеры схем эксперимента 2. Цель работы: проверить, влияет ли температура воды на развитие сапролегниевых грибов в водоеме; и если влияет – то как? Апрель-Октябрь20 стационарных точек крепления приманок. Постановка приманок каждый понедельник. Проверка интенсивности развития сапролегниевых по балльной шкале. 2 недели инкубации Замер температуры воды в 7 и 15 часов. Каждый день (или пн-ср-пт)
 Запись результатов в журнал
Запись результатов в журнал
 Оформление данных в электронном виде Excel
Оформление данных в электронном виде Excel
 Microsoft Excel удобен для хранения данных; проведения вычислений (в т. ч. статистических); построения графиков.
Microsoft Excel удобен для хранения данных; проведения вычислений (в т. ч. статистических); построения графиков.
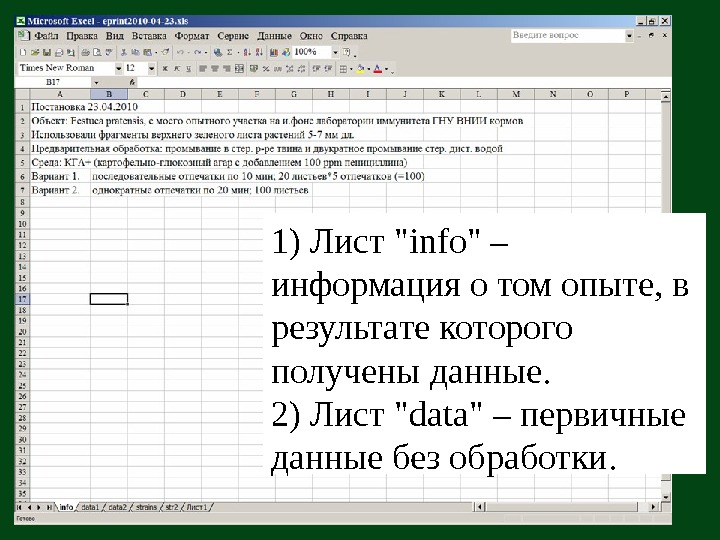
 1) Лист «info» – информация о том опыте, в результате которого получены данные. 2) Лист «data» – первичные данные без обработки.
1) Лист «info» – информация о том опыте, в результате которого получены данные. 2) Лист «data» – первичные данные без обработки.

 2. Таксономический анализ. Анализ видового состава 1. Видовое богатство – число видов. ВИД Sfmnbg’kj bhsfgnm Sdnjhm fdsh Sgnj hgsnn Sdmgm nbfgn Nhngfdnh gdfnmhgm Nbdfgnhn nhdnh Sdnbgfn bdsgag Sgfhgh mjymk Mnthm tkjej jerjdgh oi; lkfj Gh, lkjhkmj tmhj, f Wbfdgbhr bgnh Wbfvghb njhm Jkji. l. f begrnhj Shgyrjj mjm, k, Mnhb v 3 werf Dfbhfkj k, l, kyo; l; ’ kilkt ОТДЕЛ Число видов Chlorophyta 54 Rhodophyta 1 Ochrophyta 127 Cyanophyta 23 Dynophyta
2. Таксономический анализ. Анализ видового состава 1. Видовое богатство – число видов. ВИД Sfmnbg’kj bhsfgnm Sdnjhm fdsh Sgnj hgsnn Sdmgm nbfgn Nhngfdnh gdfnmhgm Nbdfgnhn nhdnh Sdnbgfn bdsgag Sgfhgh mjymk Mnthm tkjej jerjdgh oi; lkfj Gh, lkjhkmj tmhj, f Wbfdgbhr bgnh Wbfvghb njhm Jkji. l. f begrnhj Shgyrjj mjm, k, Mnhb v 3 werf Dfbhfkj k, l, kyo; l; ’ kilkt ОТДЕЛ Число видов Chlorophyta 54 Rhodophyta 1 Ochrophyta 127 Cyanophyta 23 Dynophyta
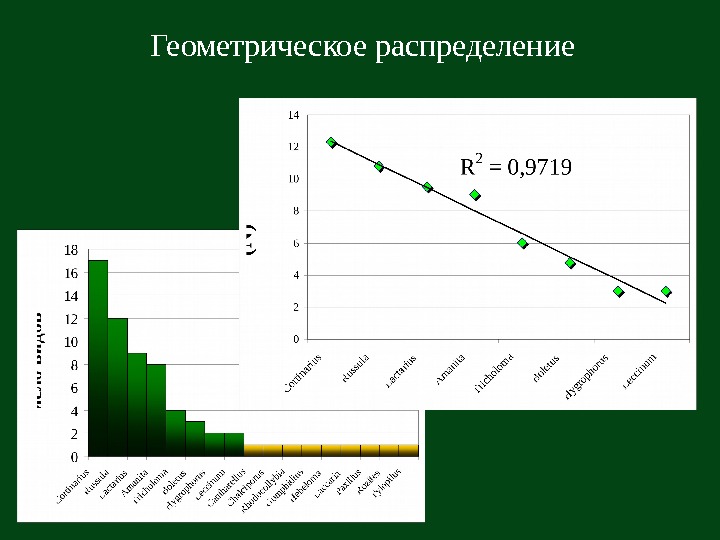
 Таксономическую структуру можно рассматривать как распределение, где значением величины является таксон, а ее частотой – богатство этого таксона. Сравнение распределений – критерий χ 2.
Таксономическую структуру можно рассматривать как распределение, где значением величины является таксон, а ее частотой – богатство этого таксона. Сравнение распределений – критерий χ 2.
 Геометрическое распределение
Геометрическое распределение
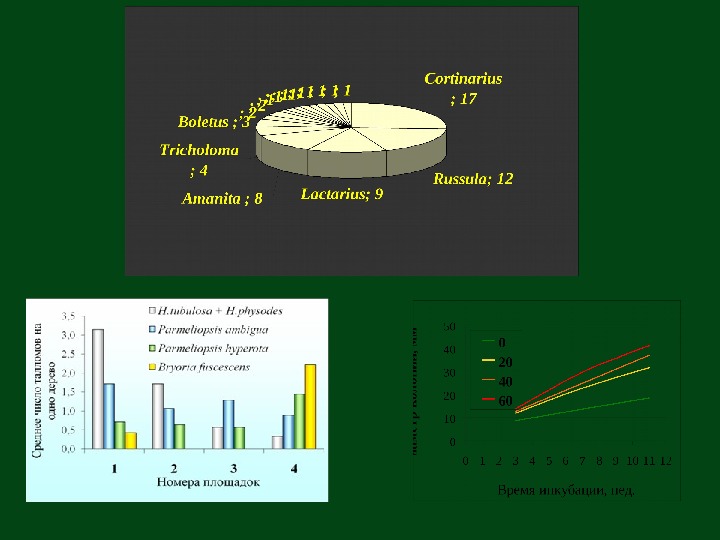
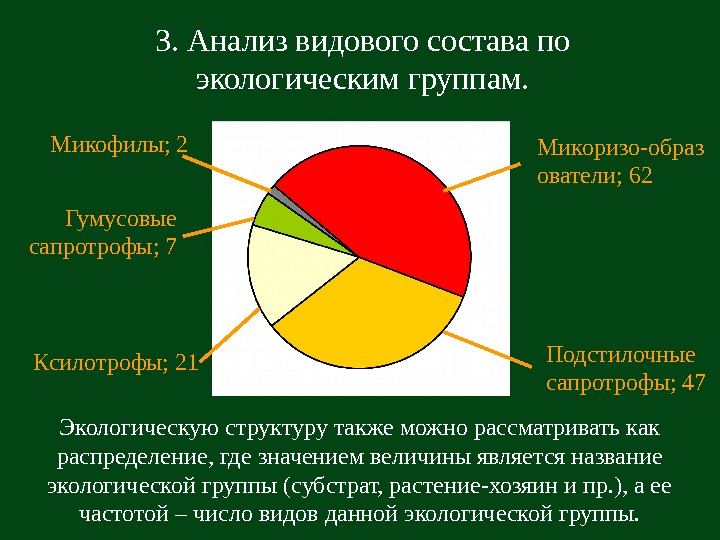
 3. Анализ видового состава по экологическим группам. Экологическую структуру также можно рассматривать как распределение, где значением величины является название экологической группы (субстрат, растение-хозяин и пр. ), а ее частотой – число видов данной экологической группы. Микоризо-образ ователи; 62 Подстилочные сапротрофы; 47 Ксилотрофы; 21 Гумусовые сапротрофы; 7 Микофилы;
3. Анализ видового состава по экологическим группам. Экологическую структуру также можно рассматривать как распределение, где значением величины является название экологической группы (субстрат, растение-хозяин и пр. ), а ее частотой – число видов данной экологической группы. Микоризо-образ ователи; 62 Подстилочные сапротрофы; 47 Ксилотрофы; 21 Гумусовые сапротрофы; 7 Микофилы;
 A cremonium rutilum 67 Acremonium sp. sect. Nectrioidea 58 Verticillium luteoalbum 54 Heleococcum alkalinum 46 Acremonium strictum 42 Papulaspora sp. 38 Acremonium charticola 29 Acremonium alcalophilum 17 Scopulariopsis brevicaulis 17 Cladosporium sphaerospermum 13 Verticillium chlamydosporium 8 Что могут означать цифры? 4. Анализ встречаемости видов.
A cremonium rutilum 67 Acremonium sp. sect. Nectrioidea 58 Verticillium luteoalbum 54 Heleococcum alkalinum 46 Acremonium strictum 42 Papulaspora sp. 38 Acremonium charticola 29 Acremonium alcalophilum 17 Scopulariopsis brevicaulis 17 Cladosporium sphaerospermum 13 Verticillium chlamydosporium 8 Что могут означать цифры? 4. Анализ встречаемости видов.
 A cremonium rutilum 67 Acremonium sp. sect. Nectrioidea 58 Verticillium luteoalbum 54 Heleococcum alkalinum 46 Acremonium strictum 42 Papulaspora sp. 38 Acremonium charticola 29 Acremonium alcalophilum 17 Scopulariopsis brevicaulis 17 Cladosporium sphaerospermum 13 Verticillium chlamydosporium 8 Alternaria alternata Bipolaris cynodontis Epicoccum purpurascens Fusarium acuminatum F usarium avenaceum. F usarium graminearum F usarium poae F usarium sambucinum Phoma pomorum значение частота значение I. II.
A cremonium rutilum 67 Acremonium sp. sect. Nectrioidea 58 Verticillium luteoalbum 54 Heleococcum alkalinum 46 Acremonium strictum 42 Papulaspora sp. 38 Acremonium charticola 29 Acremonium alcalophilum 17 Scopulariopsis brevicaulis 17 Cladosporium sphaerospermum 13 Verticillium chlamydosporium 8 Alternaria alternata Bipolaris cynodontis Epicoccum purpurascens Fusarium acuminatum F usarium avenaceum. F usarium graminearum F usarium poae F usarium sambucinum Phoma pomorum значение частота значение I. II.
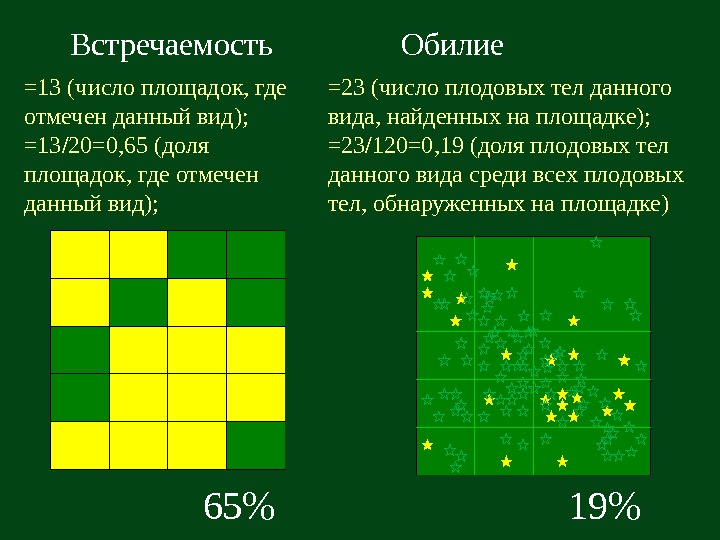
 Встречаемость Обилие =13 (число площадок, где отмечен данный вид); =13 / 20=0, 65 (доля площадок, где отмечен данный вид); =23 (число плодовых тел данного вида, найденных на площадке); =23 / 120=0, 19 (доля плодовых тел данного вида среди всех плодовых тел, обнаруженных на площадке) 65% 19%
Встречаемость Обилие =13 (число площадок, где отмечен данный вид); =13 / 20=0, 65 (доля площадок, где отмечен данный вид); =23 (число плодовых тел данного вида, найденных на площадке); =23 / 120=0, 19 (доля плодовых тел данного вида среди всех плодовых тел, обнаруженных на площадке) 65% 19%
 Пусть a i – относительная встречаемость i — того вида, а b i – его относительное обилие. a i = k i / KЧисло площадок, где отмечен вид i 0< k i < K Общее число площадок b i = n i / N 0< n i < N ; Σ n i = NЧисло плодовых тел вида i Общее число плодовых тел 0 < Σ a i ≤ i Σ b i =
Пусть a i – относительная встречаемость i — того вида, а b i – его относительное обилие. a i = k i / KЧисло площадок, где отмечен вид i 0< k i < K Общее число площадок b i = n i / N 0< n i < N ; Σ n i = NЧисло плодовых тел вида i Общее число плодовых тел 0 < Σ a i ≤ i Σ b i =
 Единицы учета Особь (клетка одноклеточных водорослей) КОЕ – колониеобразующая единица. Плодовое тело Организм-хозяин
Единицы учета Особь (клетка одноклеточных водорослей) КОЕ – колониеобразующая единица. Плодовое тело Организм-хозяин
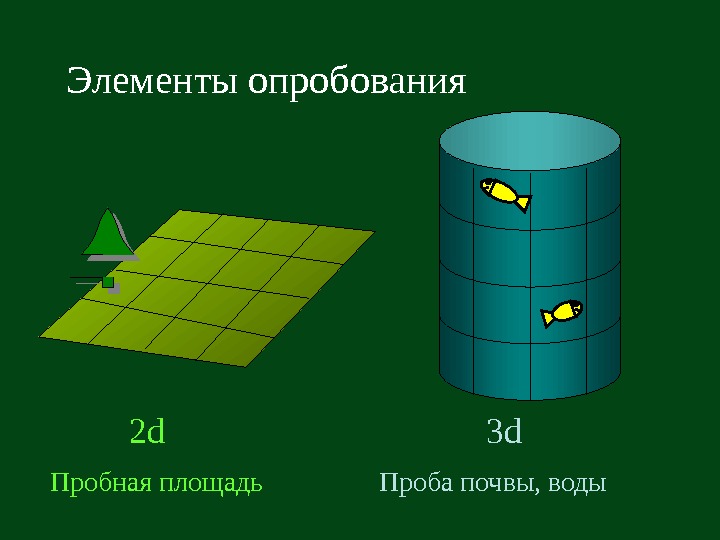
 Элементы опробования Пробная площадь 2 d Проба почвы, воды 3 d
Элементы опробования Пробная площадь 2 d Проба почвы, воды 3 d
 x i n i Acremonium alcalophilum 17 Acremonium charticola 29 A cremonium rutilum 67 Acremonium strictum 42 Cladosporium sphaerospermum 13 Heleococcum alkalinum 46 Scopulariopsis brevicaulis 17 Verticillium chlamydosporium 8 Verticillium luteoalbum 54 x i n i A cremonium rutilum 67 Verticillium luteoalbum 54 Heleococcum alkalinum 46 Acremonium strictum 42 Acremonium charticola 29 Acremonium alcalophilum 17 Scopulariopsis brevicaulis 17 Cladosporium sphaerospermum 13 Verticillium chlamydosporium 8 Обработка данных. Ранжирование
x i n i Acremonium alcalophilum 17 Acremonium charticola 29 A cremonium rutilum 67 Acremonium strictum 42 Cladosporium sphaerospermum 13 Heleococcum alkalinum 46 Scopulariopsis brevicaulis 17 Verticillium chlamydosporium 8 Verticillium luteoalbum 54 x i n i A cremonium rutilum 67 Verticillium luteoalbum 54 Heleococcum alkalinum 46 Acremonium strictum 42 Acremonium charticola 29 Acremonium alcalophilum 17 Scopulariopsis brevicaulis 17 Cladosporium sphaerospermum 13 Verticillium chlamydosporium 8 Обработка данных. Ранжирование
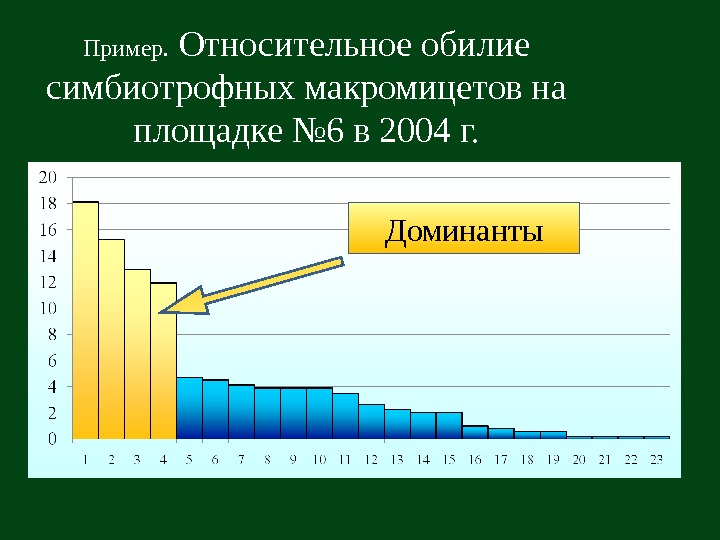
 Пример. Относительное обилие симбиотрофных макромицетов на площадке № 6 в 2004 г. Доминанты
Пример. Относительное обилие симбиотрофных макромицетов на площадке № 6 в 2004 г. Доминанты
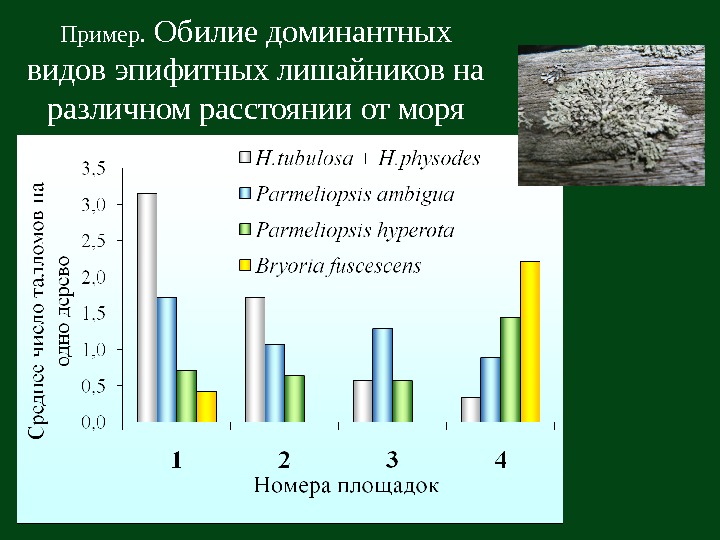
 Пример. Обилие доминантных видов эпифитных лишайников на различном расстоянии от моря
Пример. Обилие доминантных видов эпифитных лишайников на различном расстоянии от моря
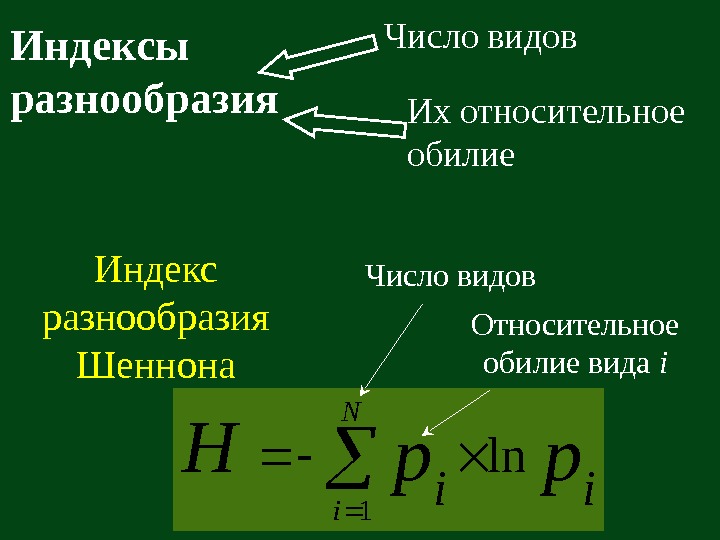
 Индексы разнообразия Индекс разнообразия Шеннонаpp. H ii N i ln 1 Относительное обилие вида i. Число видов Их относительное обилие
Индексы разнообразия Индекс разнообразия Шеннонаpp. H ii N i ln 1 Относительное обилие вида i. Число видов Их относительное обилие
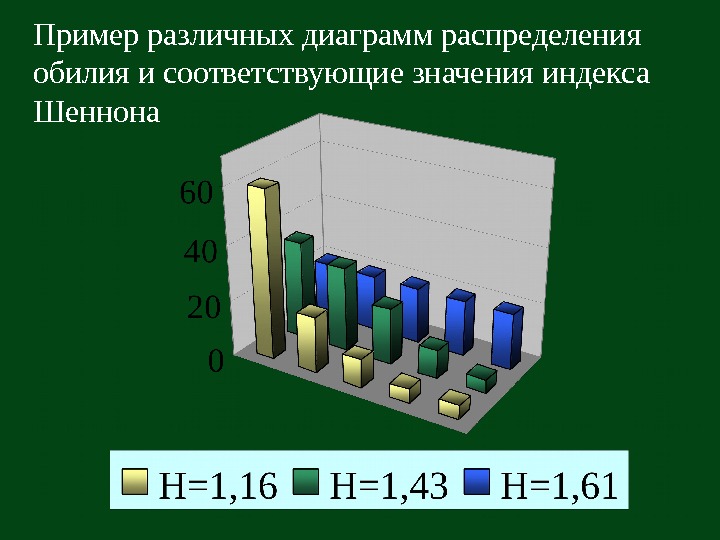
 Пример различных диаграмм распределения обилия и соответствующие значения индекса Шеннона
Пример различных диаграмм распределения обилия и соответствующие значения индекса Шеннона
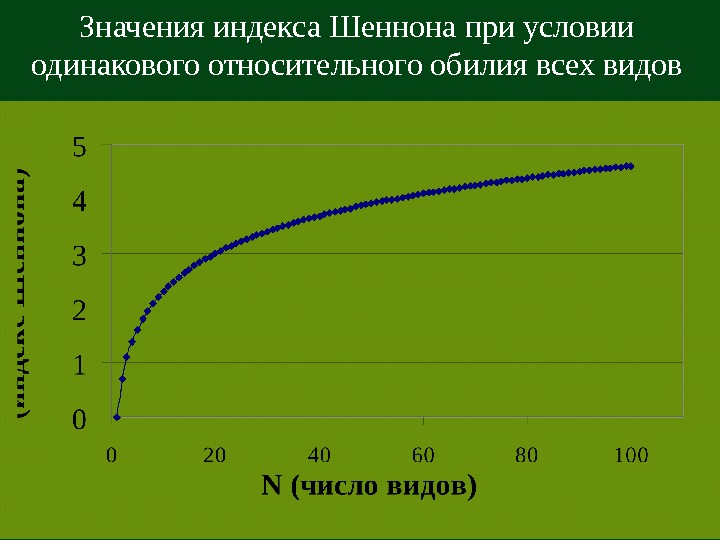
 Значения индекса Шеннона при условии одинакового относительного обилия всех видов
Значения индекса Шеннона при условии одинакового относительного обилия всех видов
 Индекс разнообразия Шеннона Н обычно принимает значения в интервале 1, 5 -3, 5 ; крайне редко он превышает величину 4, 5 Проверка гипотезы о равенстве двух индексов Шеннона с помощью t — критерия: Э. Мэгарран, 1992. Экологическое разнообразие и его измерение. С. 41 -42; 143 -146. Н предполагает, что «особи» отобраны случайно (1) из неопределенно большой совокупности (2) , причем обнаружены все виды (3).
Индекс разнообразия Шеннона Н обычно принимает значения в интервале 1, 5 -3, 5 ; крайне редко он превышает величину 4, 5 Проверка гипотезы о равенстве двух индексов Шеннона с помощью t — критерия: Э. Мэгарран, 1992. Экологическое разнообразие и его измерение. С. 41 -42; 143 -146. Н предполагает, что «особи» отобраны случайно (1) из неопределенно большой совокупности (2) , причем обнаружены все виды (3).
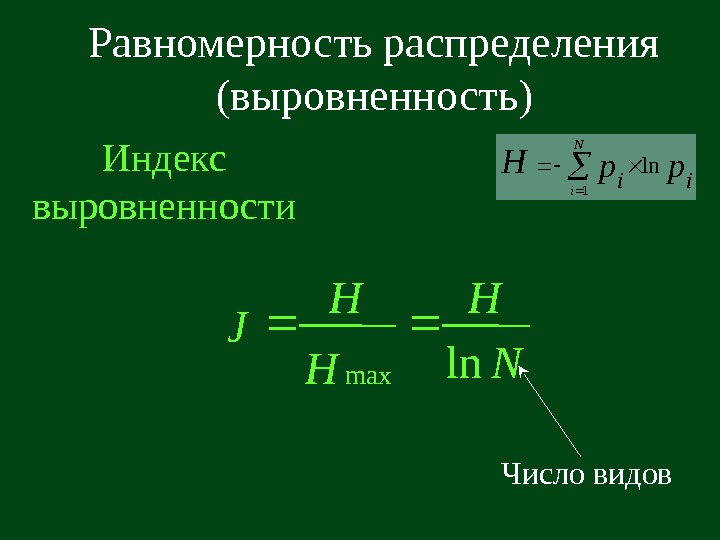
 Равномерность распределения (выровненность) Индекс выровненности pp. H ii. N i ln 1 Число видов. NH H H J ln max
Равномерность распределения (выровненность) Индекс выровненности pp. H ii. N i ln 1 Число видов. NH H H J ln max
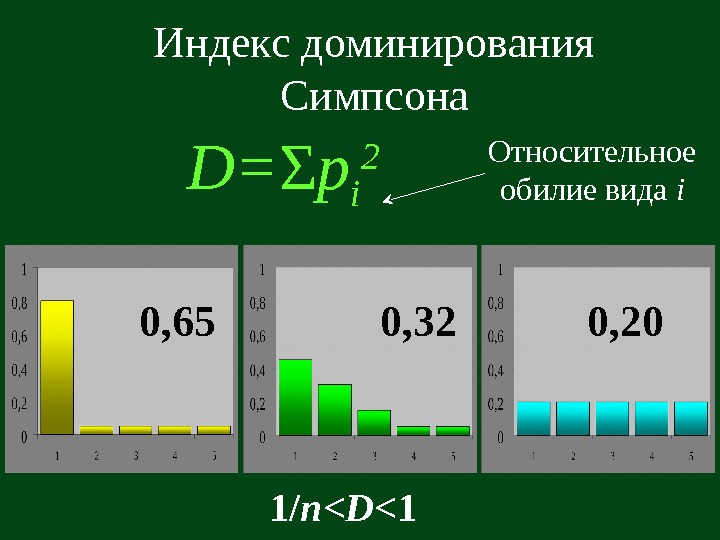
 Индекс доминирования Симпсона D= Σ p i 2 Относительное обилие вида i 0, 65 0, 32 0, 20 1/ n < D <
Индекс доминирования Симпсона D= Σ p i 2 Относительное обилие вида i 0, 65 0, 32 0, 20 1/ n < D <
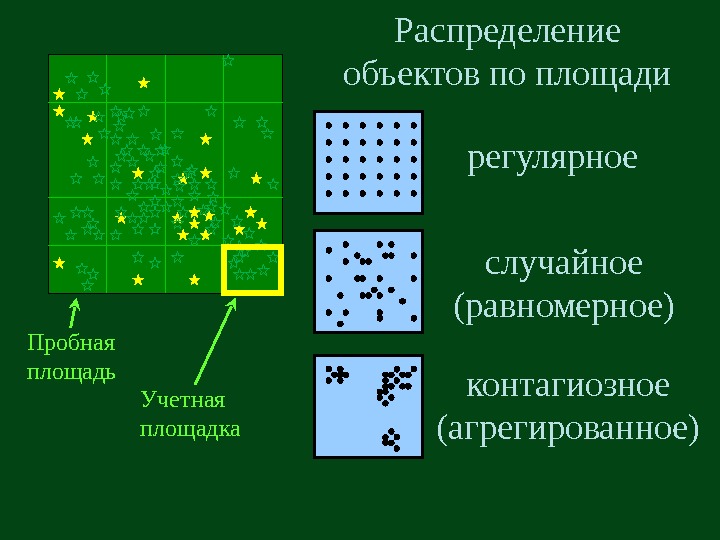
 Распределение объектов по площади регулярное случайное (равномерное) контагиозное (агрегированное)Пробная площадь Учетная площадка
Распределение объектов по площади регулярное случайное (равномерное) контагиозное (агрегированное)Пробная площадь Учетная площадка
 Ложноконтагиозное распределение
Ложноконтагиозное распределение
 Ложноконтагиозное распределение Мо. Мо рере Суш а
Ложноконтагиозное распределение Мо. Мо рере Суш а
 Индекс Морисита I M = M Σ n i ( n i – 1) N ( N -1)i =1 MЧисло площадок Число особей вида на i- той площадке Общее число особей вида на всех площадках; N = Σ n i I M 1 – контагиозное размещение; I M = M – резко контагиозное размещение , все особи на одной площадке.
Индекс Морисита I M = M Σ n i ( n i – 1) N ( N -1)i =1 MЧисло площадок Число особей вида на i- той площадке Общее число особей вида на всех площадках; N = Σ n i I M 1 – контагиозное размещение; I M = M – резко контагиозное размещение , все особи на одной площадке.
 I M = M Σ n i ( n i – 1) N ( N -1) 1 1 0 0 3 0 1 0 0 0 2 1 0 1 6 3 1 1 1 0 I M = 22*2120*(3*2+2*1+6*5+3*2) = =20*44/(22*21)=1, 9 I M >1 – контагиозное распределение плодовых тел.
I M = M Σ n i ( n i – 1) N ( N -1) 1 1 0 0 3 0 1 0 0 0 2 1 0 1 6 3 1 1 1 0 I M = 22*2120*(3*2+2*1+6*5+3*2) = =20*44/(22*21)=1, 9 I M >1 – контагиозное распределение плодовых тел.
 Коэффициенты сходства 1. 0 < K <1. 2. K =1, если площадки совпадают по видовому составу. 3. Значение коэффициента не зависит от того, сравнивают ли первую площадку со второй, или вторую с первой. 4. K = 0 , если площадки не совпадают ни по одному виду.
Коэффициенты сходства 1. 0 < K <1. 2. K =1, если площадки совпадают по видовому составу. 3. Значение коэффициента не зависит от того, сравнивают ли первую площадку со второй, или вторую с первой. 4. K = 0 , если площадки не совпадают ни по одному виду.
 K j =c/(a+b-c)Коэффициент Жаккара число общих видов число видов на первой площадке число видов на второй площадке Jaccard,
K j =c/(a+b-c)Коэффициент Жаккара число общих видов число видов на первой площадке число видов на второй площадке Jaccard,
 № 1 № 2 Alternaria alternata (Fr. ) Keissler + + Bipolaris cynodontis (Marig. ) Shoem. — + Epicoccum purpurascens Ehrenb. ex Schlecht. + + Fusarium acuminatum Ell. et Kellern + — F usarium avenaceum (Fr. ) Sacc. — + F usarium graminearum Schwabe + — F usarium poae (Peck) Wollenw. + — F usarium sambucinum Fuckel + + Phoma pomorum Thum. + -Пример. Эпифиты злаков 7 5 K j =3/(7+5 -3)=3/9 =33% K j =c/(a+b-c)
№ 1 № 2 Alternaria alternata (Fr. ) Keissler + + Bipolaris cynodontis (Marig. ) Shoem. — + Epicoccum purpurascens Ehrenb. ex Schlecht. + + Fusarium acuminatum Ell. et Kellern + — F usarium avenaceum (Fr. ) Sacc. — + F usarium graminearum Schwabe + — F usarium poae (Peck) Wollenw. + — F usarium sambucinum Fuckel + + Phoma pomorum Thum. + -Пример. Эпифиты злаков 7 5 K j =3/(7+5 -3)=3/9 =33% K j =c/(a+b-c)
 K s =2 c/(a+b)Коэффициент Съеренсена число общих видов число видов на первой площадке число видов на второй площадке Sørensen,
K s =2 c/(a+b)Коэффициент Съеренсена число общих видов число видов на первой площадке число видов на второй площадке Sørensen,
 № 1 № 2 Alternaria alternata (Fr. ) Keissler + + Bipolaris cynodontis (Marig. ) Shoem. — + Epicoccum purpurascens Ehrenb. ex Schlecht. + + Fusarium acuminatum Ell. et Kellern + — F usarium avenaceum (Fr. ) Sacc. — + F usarium graminearum Schwabe + — F usarium poae (Peck) Wollenw. + — F usarium sambucinum Fuckel + + Phoma pomorum Thum. + -Пример. Эпифиты злаков 7 5 K S =2 3/(7+5)=6/12 =50% K s =2 c/(a+b)
№ 1 № 2 Alternaria alternata (Fr. ) Keissler + + Bipolaris cynodontis (Marig. ) Shoem. — + Epicoccum purpurascens Ehrenb. ex Schlecht. + + Fusarium acuminatum Ell. et Kellern + — F usarium avenaceum (Fr. ) Sacc. — + F usarium graminearum Schwabe + — F usarium poae (Peck) Wollenw. + — F usarium sambucinum Fuckel + + Phoma pomorum Thum. + -Пример. Эпифиты злаков 7 5 K S =2 3/(7+5)=6/12 =50% K s =2 c/(a+b)
 Пример. Микромицеты содовых солончаков Кулундинской степи Выделено на щелочной агар (р. Н 10, 0) 18 видов Выделено на другие среды 21 вид Число видов, выделяющихся в обоих случаях 8 видов K s =2 8 /( 18 + 21 ) =16/39 41%
Пример. Микромицеты содовых солончаков Кулундинской степи Выделено на щелочной агар (р. Н 10, 0) 18 видов Выделено на другие среды 21 вид Число видов, выделяющихся в обоих случаях 8 видов K s =2 8 /( 18 + 21 ) =16/39 41%
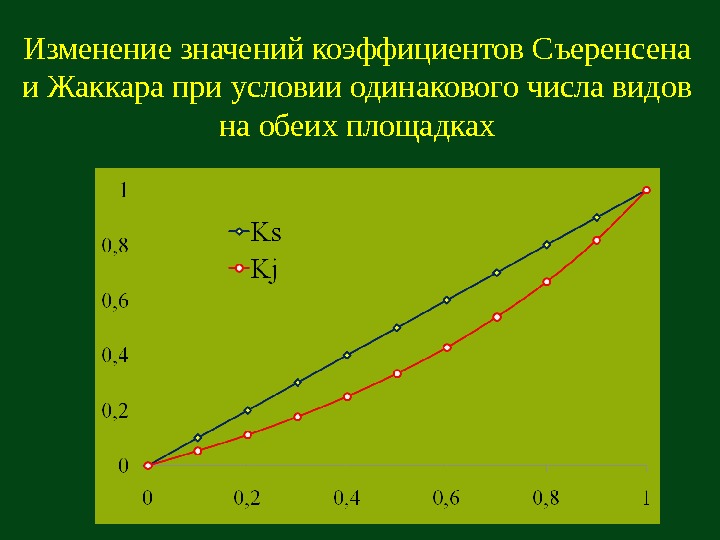
 Изменение значений коэффициентов Съеренсена и Жаккара при условии одинакового числа видов на обеих площадках
Изменение значений коэффициентов Съеренсена и Жаккара при условии одинакового числа видов на обеих площадках
 K ’ s =Коэффициент Съеренсена — Ч екановского количественные значения вида i на площадке B 2 Σ min (A i , B i ) i = 1 k Σ A i + i = 1 k Σ B i i = 1 k количественные значения вида i на площадке A K s =2 c/(a+b)
K ’ s =Коэффициент Съеренсена — Ч екановского количественные значения вида i на площадке B 2 Σ min (A i , B i ) i = 1 k Σ A i + i = 1 k Σ B i i = 1 k количественные значения вида i на площадке A K s =2 c/(a+b)
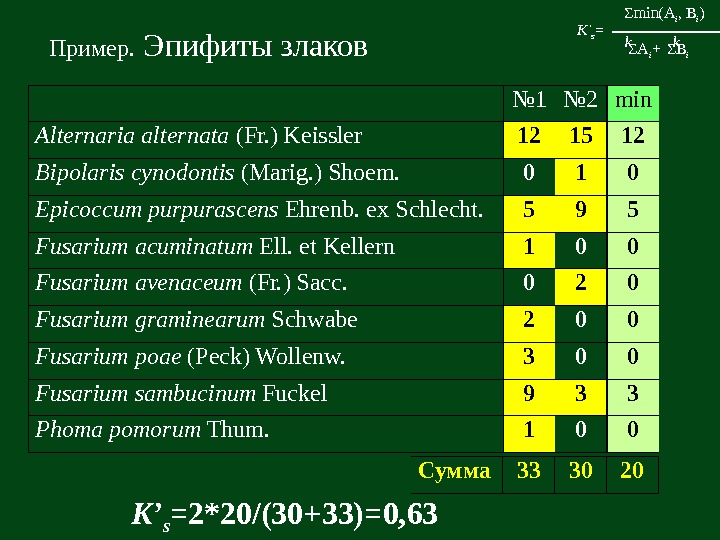
 № 1 № 2 Alternaria alternata (Fr. ) Keissler 12 15 Bipolaris cynodontis (Marig. ) Shoem. 0 1 Epicoccum purpurascens Ehrenb. ex Schlecht. 5 9 Fusarium acuminatum Ell. et Kellern 1 0 F usarium avenaceum (Fr. ) Sacc. 0 2 F usarium graminearum Schwabe 2 0 F usarium poae (Peck) Wollenw. 3 0 F usarium sambucinum Fuckel 9 3 Phoma pomorum Thum. 1 0 Пример. Эпифиты злаков Сумма 33 30 20 min 12 0 5 0 0 3 0 K’ s = 2* 20/(30+33)=0, 63 K ’ s = Σ min(A i , B i )k Σ A i +k Σ B ik
№ 1 № 2 Alternaria alternata (Fr. ) Keissler 12 15 Bipolaris cynodontis (Marig. ) Shoem. 0 1 Epicoccum purpurascens Ehrenb. ex Schlecht. 5 9 Fusarium acuminatum Ell. et Kellern 1 0 F usarium avenaceum (Fr. ) Sacc. 0 2 F usarium graminearum Schwabe 2 0 F usarium poae (Peck) Wollenw. 3 0 F usarium sambucinum Fuckel 9 3 Phoma pomorum Thum. 1 0 Пример. Эпифиты злаков Сумма 33 30 20 min 12 0 5 0 0 3 0 K’ s = 2* 20/(30+33)=0, 63 K ’ s = Σ min(A i , B i )k Σ A i +k Σ B ik
 Коэффициент Морисита K M = 2 Σ n 1 i n 2 i ( λ 1 + λ 2 ) N 1 N 2 λ 1 = Σ n 1 i ( n 1 i -1) N 1 ( N 1 -1) N 1 = Σ n 1 ii= 1 k Morisita, 1959 Обилие i- того вида в первом и во втором сообществах Суммарное обилие видов в первом и во втором сообществах
Коэффициент Морисита K M = 2 Σ n 1 i n 2 i ( λ 1 + λ 2 ) N 1 N 2 λ 1 = Σ n 1 i ( n 1 i -1) N 1 ( N 1 -1) N 1 = Σ n 1 ii= 1 k Morisita, 1959 Обилие i- того вида в первом и во втором сообществах Суммарное обилие видов в первом и во втором сообществах
 № 1 № 2 Alternaria alternata 12 15 Bipolaris cynodontis 0 1 Epicoccum purpurascens 5 9 Fusarium acuminatum 1 0 F usarium avenaceum 0 2 F usarium graminearum 2 0 F usarium poae 3 0 F usarium sambucinum 9 3 Phoma pomorum 1 0 Пример. Эпифиты злаков Сумма 33 30 K M = 2* (12*15+5*9+9*3)/((0, 33+0, 22)*30*33)=0, 92 λ 1 = (12*11+5*4+2*1+ +3*2+9*8)/(33*32)= =0, 22 λ 2 = (15*14+9*8+2*1+ +3*2)/(30*29)= =0,
№ 1 № 2 Alternaria alternata 12 15 Bipolaris cynodontis 0 1 Epicoccum purpurascens 5 9 Fusarium acuminatum 1 0 F usarium avenaceum 0 2 F usarium graminearum 2 0 F usarium poae 3 0 F usarium sambucinum 9 3 Phoma pomorum 1 0 Пример. Эпифиты злаков Сумма 33 30 K M = 2* (12*15+5*9+9*3)/((0, 33+0, 22)*30*33)=0, 92 λ 1 = (12*11+5*4+2*1+ +3*2+9*8)/(33*32)= =0, 22 λ 2 = (15*14+9*8+2*1+ +3*2)/(30*29)= =0,
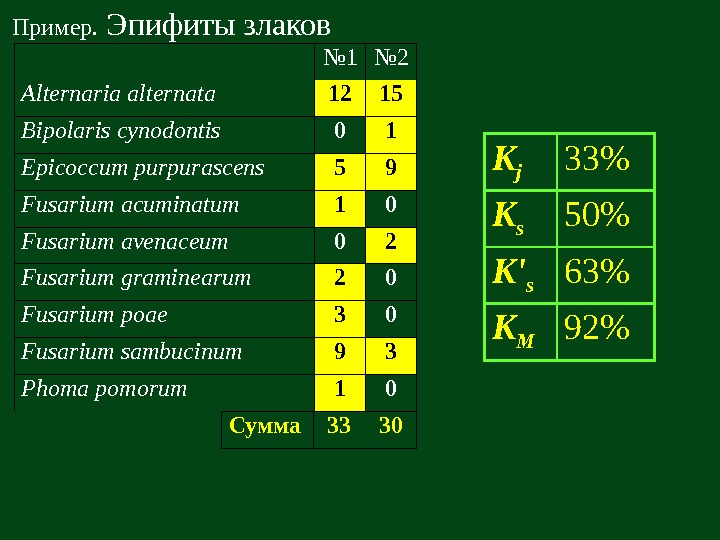
 № 1 № 2 Alternaria alternata 12 15 Bipolaris cynodontis 0 1 Epicoccum purpurascens 5 9 Fusarium acuminatum 1 0 F usarium avenaceum 0 2 F usarium graminearum 2 0 F usarium poae 3 0 F usarium sambucinum 9 3 Phoma pomorum 1 0 Пример. Эпифиты злаков Сумма 33 30 K j 33% K s 50% K’ s 63% K M 92%
№ 1 № 2 Alternaria alternata 12 15 Bipolaris cynodontis 0 1 Epicoccum purpurascens 5 9 Fusarium acuminatum 1 0 F usarium avenaceum 0 2 F usarium graminearum 2 0 F usarium poae 3 0 F usarium sambucinum 9 3 Phoma pomorum 1 0 Пример. Эпифиты злаков Сумма 33 30 K j 33% K s 50% K’ s 63% K M 92%
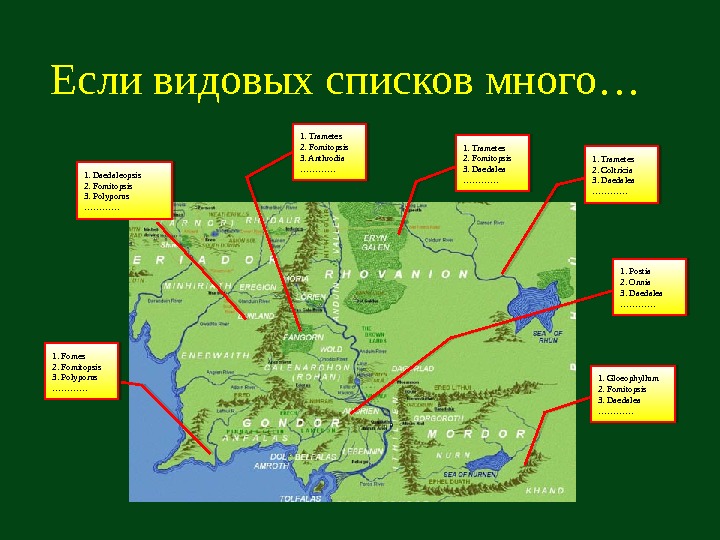
 Если видовых списков много… 1. Gloeophyllum 2. Fomitopsis 3. Daedalea ………… 1. Postia 2. Onnia 3. Daedalea ………… 1. Trametes 2. Coltricia 3. Daedalea ………… 1. Trametes 2. Fomitopsis 3. Anthrodia ………… 1. Daedaleopsis 2. Fomitopsis 3. Polyporus ………… 1. Fomes 2. Fomitopsis 3. Polyporus …………
Если видовых списков много… 1. Gloeophyllum 2. Fomitopsis 3. Daedalea ………… 1. Postia 2. Onnia 3. Daedalea ………… 1. Trametes 2. Coltricia 3. Daedalea ………… 1. Trametes 2. Fomitopsis 3. Anthrodia ………… 1. Daedaleopsis 2. Fomitopsis 3. Polyporus ………… 1. Fomes 2. Fomitopsis 3. Polyporus …………
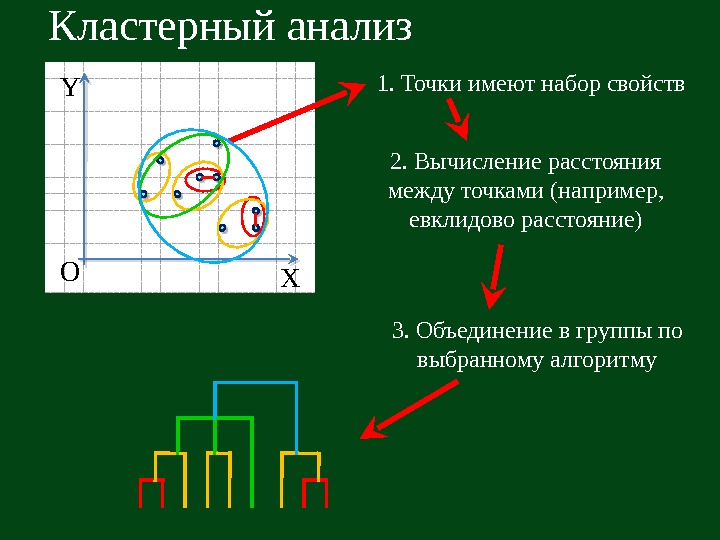
 Кластерный анализ Y XO 1. Точки имеют набор свойств 2. Вычисление расстояния между точками (например, евклидово расстояние) 3. Объединение в группы по выбранному алгоритму
Кластерный анализ Y XO 1. Точки имеют набор свойств 2. Вычисление расстояния между точками (например, евклидово расстояние) 3. Объединение в группы по выбранному алгоритму
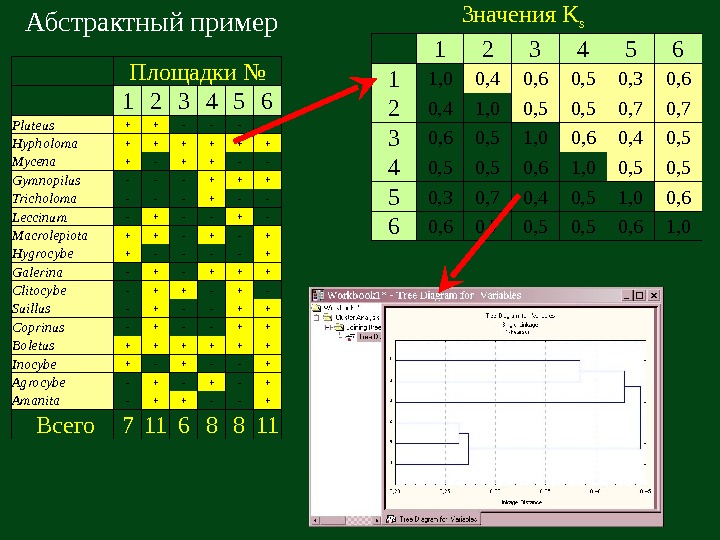
 Абстрактный пример Площадки № 1 2 3 4 5 6 Pluteus + + — — Hypholoma + + + Mycena + — + + — — Gymnopilus — — — + + + Tricholoma — — — + — — Leccinum — + — Macrolepiota + + — + Hygrocybe + — — + Galerina — + + + Clitocybe — + + — Suillus — + — — + + Coprinus — + — — + + Boletus + + + Inocybe + — — + Agrocybe — + — + Amanita — + + — — + Всего 7 11 6 8 8 11 1 2 3 4 5 6 1 1, 0 0, 4 0, 6 0, 5 0, 3 0, 6 2 0, 4 1, 0 0, 5 0, 7 3 0, 6 0, 5 1, 0 0, 6 0, 4 0, 5 0, 6 1, 0 0, 5 5 0, 3 0, 7 0, 4 0, 5 1, 0 0, 6 6 0, 7 0, 5 0, 6 1, 0 Значения K s
Абстрактный пример Площадки № 1 2 3 4 5 6 Pluteus + + — — Hypholoma + + + Mycena + — + + — — Gymnopilus — — — + + + Tricholoma — — — + — — Leccinum — + — Macrolepiota + + — + Hygrocybe + — — + Galerina — + + + Clitocybe — + + — Suillus — + — — + + Coprinus — + — — + + Boletus + + + Inocybe + — — + Agrocybe — + — + Amanita — + + — — + Всего 7 11 6 8 8 11 1 2 3 4 5 6 1 1, 0 0, 4 0, 6 0, 5 0, 3 0, 6 2 0, 4 1, 0 0, 5 0, 7 3 0, 6 0, 5 1, 0 0, 6 0, 4 0, 5 0, 6 1, 0 0, 5 5 0, 3 0, 7 0, 4 0, 5 1, 0 0, 6 6 0, 7 0, 5 0, 6 1, 0 Значения K s
 Коэффициенты сходства Собственно коэффициенты сходства тем или иным образом выражают отношение числа совпадающих признаков к общему числу. Кроме коэффициентов сходства существуют т. н. меры расстояния , определяющие различия в многомерном пространстве признаков и вероятностные меры , оценивающие вероятность того, что объекты будут различны. Меры расстояния (Для независимых признаков) Мера расстояния Евклида или Евклидово расстояние (Для зависимых признаков) Мера расстояния Махаланобиса
Коэффициенты сходства Собственно коэффициенты сходства тем или иным образом выражают отношение числа совпадающих признаков к общему числу. Кроме коэффициентов сходства существуют т. н. меры расстояния , определяющие различия в многомерном пространстве признаков и вероятностные меры , оценивающие вероятность того, что объекты будут различны. Меры расстояния (Для независимых признаков) Мера расстояния Евклида или Евклидово расстояние (Для зависимых признаков) Мера расстояния Махаланобиса
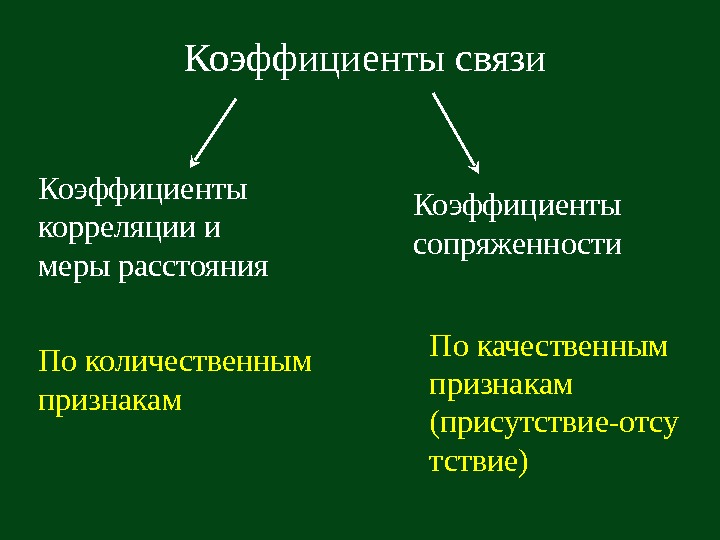
 Коэффициенты связи По количественным признакам. Коэффициенты корреляции и меры расстояния По качественным признакам (присутствие-отсу тствие)Коэффициенты сопряженности
Коэффициенты связи По количественным признакам. Коэффициенты корреляции и меры расстояния По качественным признакам (присутствие-отсу тствие)Коэффициенты сопряженности
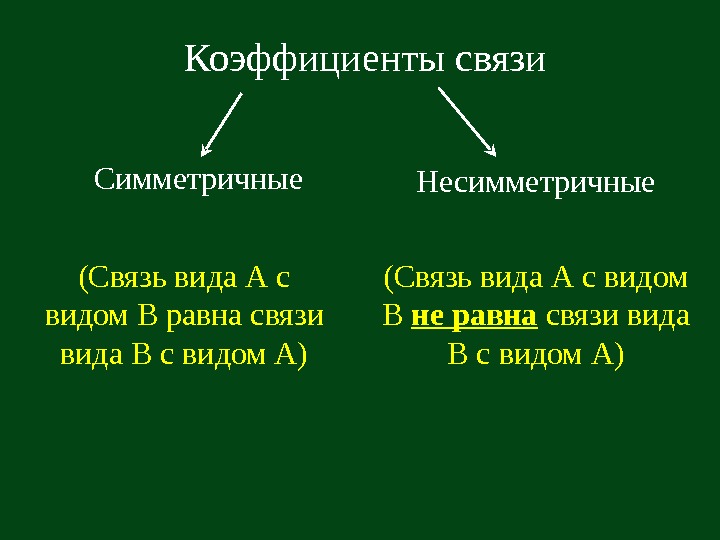
 Симметричные (Связь вида А с видом В равна связи вида В с видом А) Несимметричные. Коэффициенты связи (Связь вида А с видом В не равна связи вида В с видом А)
Симметричные (Связь вида А с видом В равна связи вида В с видом А) Несимметричные. Коэффициенты связи (Связь вида А с видом В не равна связи вида В с видом А)
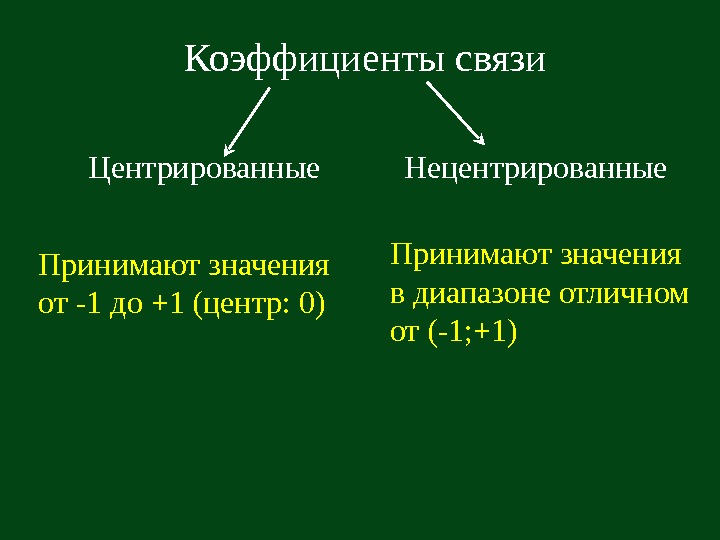
 Центрированные Принимают значения от -1 до +1 (центр: 0) Нецентрированные Принимают значения в диапазоне отличном от (-1; +1)Коэффициенты связи
Центрированные Принимают значения от -1 до +1 (центр: 0) Нецентрированные Принимают значения в диапазоне отличном от (-1; +1)Коэффициенты связи
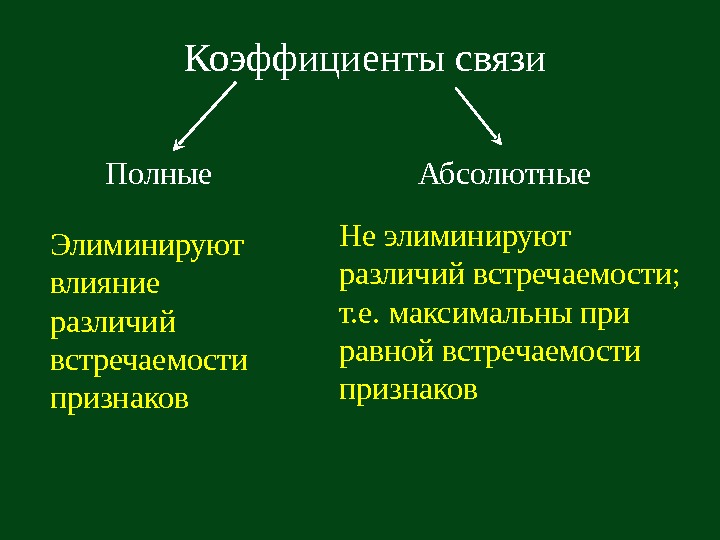
 Полные Элиминируют влияние различий встречаемости признаков Абсолютные Не элиминируют различий встречаемости; т. е. максимальны при равной встречаемости признаков. Коэффициенты связи
Полные Элиминируют влияние различий встречаемости признаков Абсолютные Не элиминируют различий встречаемости; т. е. максимальны при равной встречаемости признаков. Коэффициенты связи
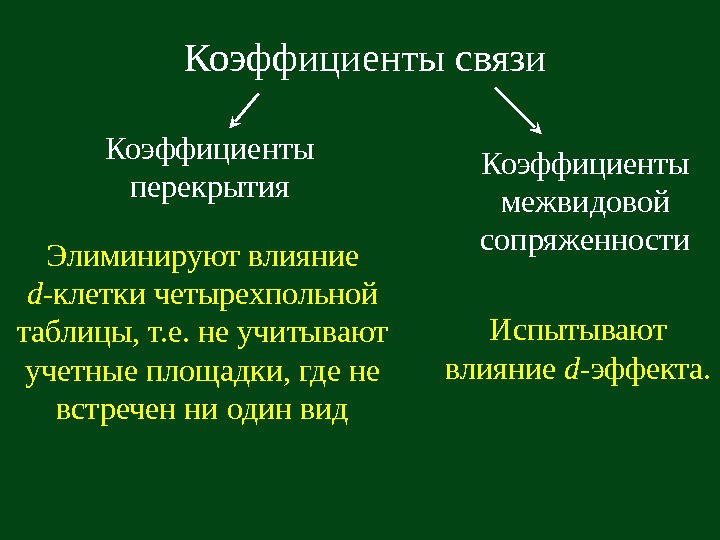
 Коэффициенты перекрытия Элиминируют влияние d- клетки четырехпольной таблицы, т. е. не учитывают учетные площадки, где не встречен ни один вид Коэффициенты межвидовой сопряженности Испытывают влияние d- эффекта. Коэффициенты связи
Коэффициенты перекрытия Элиминируют влияние d- клетки четырехпольной таблицы, т. е. не учитывают учетные площадки, где не встречен ни один вид Коэффициенты межвидовой сопряженности Испытывают влияние d- эффекта. Коэффициенты связи
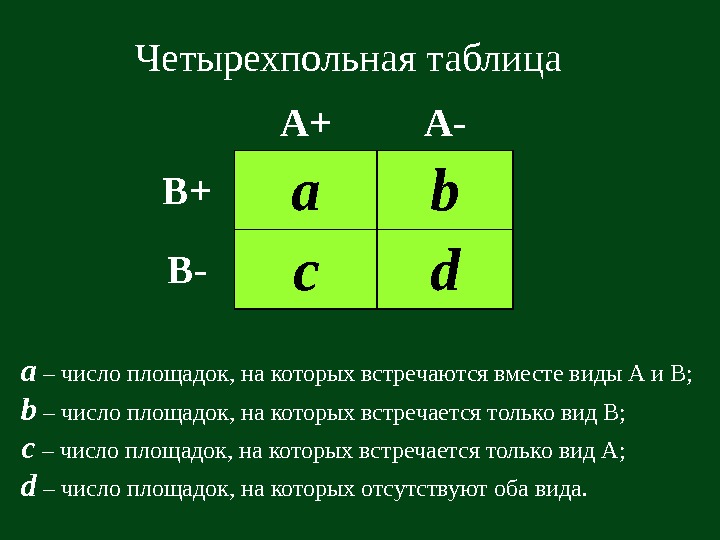
 А + А — В + a b В — c d a – число площадок, на которых встречаются вместе виды А и В; b – число площадок, на которых встречается только вид В; с – число площадок, на которых встречается только вид А; d – число площадок, на которых отсутствуют оба вида. Четырехпольная таблица
А + А — В + a b В — c d a – число площадок, на которых встречаются вместе виды А и В; b – число площадок, на которых встречается только вид В; с – число площадок, на которых встречается только вид А; d – число площадок, на которых отсутствуют оба вида. Четырехпольная таблица
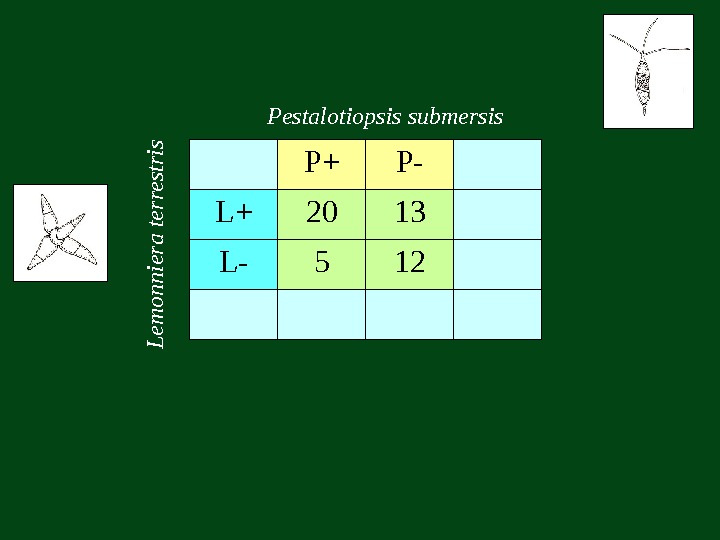
 P + P- L + 20 13 L- 5 12 Pestalotiopsis submersis. L e m o n n ie ra te rre stris
P + P- L + 20 13 L- 5 12 Pestalotiopsis submersis. L e m o n n ie ra te rre stris
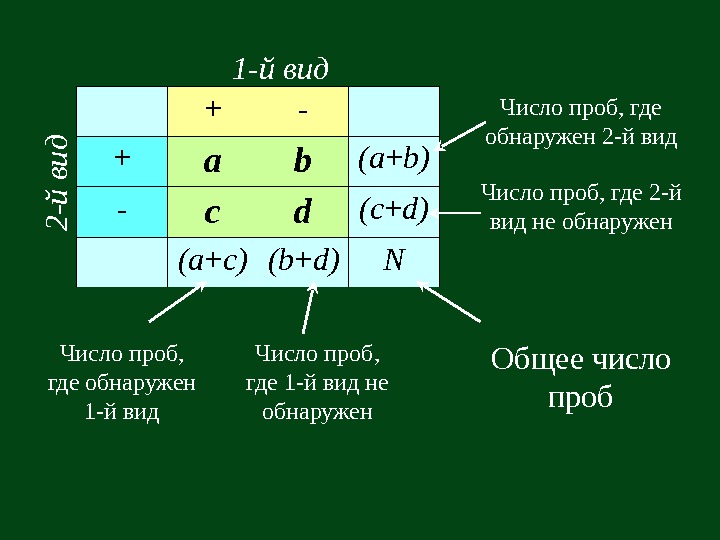
 + — + a b (a + b) — c d (c + d) (a + c) (b + d) N 1 — й вид 2 — й в и д Число проб, где обнаружен 2 -й вид Число проб, где 2 -й вид не обнаружен Число проб, где обнаружен 1 -й вид Число проб, где 1 -й вид не обнаружен Общее число проб
+ — + a b (a + b) — c d (c + d) (a + c) (b + d) N 1 — й вид 2 — й в и д Число проб, где обнаружен 2 -й вид Число проб, где 2 -й вид не обнаружен Число проб, где обнаружен 1 -й вид Число проб, где 1 -й вид не обнаружен Общее число проб
 1 — й вид 2 — й в и д Если предположить, что встречаемость обоих видов независима, то (a+b) N a’ (a+c)= a’ = (a+b)(a+c) / N+ — + a (a’) b (b’) (a+b) — c (c’) d (d’) (c+d) (a+c) (b+d) N
1 — й вид 2 — й в и д Если предположить, что встречаемость обоих видов независима, то (a+b) N a’ (a+c)= a’ = (a+b)(a+c) / N+ — + a (a’) b (b’) (a+b) — c (c’) d (d’) (c+d) (a+c) (b+d) N
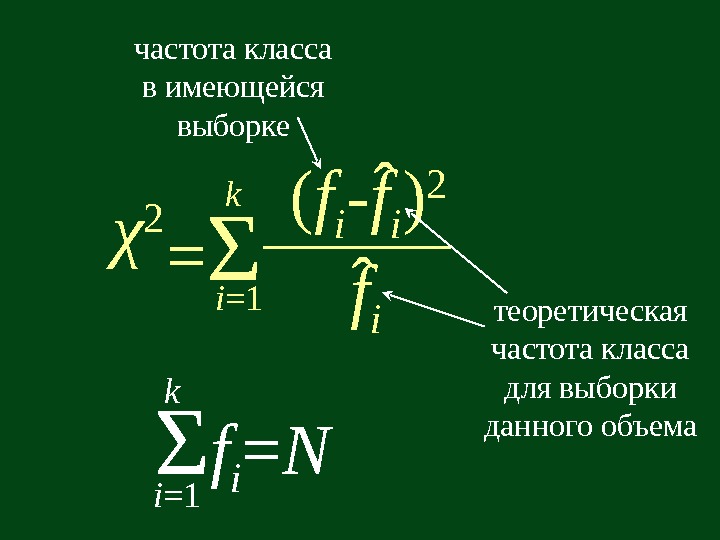
 χ 2 = Σ ( f i — f i ) 2 f iˆ ˆ теоретическая частота класса для выборки данного объемачастота класса в имеющейся выборке i =1 k Σ f i = N i =1 k
χ 2 = Σ ( f i — f i ) 2 f iˆ ˆ теоретическая частота класса для выборки данного объемачастота класса в имеющейся выборке i =1 k Σ f i = N i =1 k
 Н 0 : Выборка сделана из генеральной совокупности, распределение которой совпадает с теоретическим. Н 1 : Выборка сделана из генеральной совокупности, распределение которой не совпадает с теоретическим. χ 2 α ; ν α – уровень значимости; ν – число степеней свободы. χ 2 ≥ χ 2 α ; ν => Отвергаем H 0 χ 2 Не отвергаем H
Н 0 : Выборка сделана из генеральной совокупности, распределение которой совпадает с теоретическим. Н 1 : Выборка сделана из генеральной совокупности, распределение которой не совпадает с теоретическим. χ 2 α ; ν α – уровень значимости; ν – число степеней свободы. χ 2 ≥ χ 2 α ; ν => Отвергаем H 0 χ 2 Не отвергаем H
 Критерий χ 2 работает при теоретической частоте классов ≥
Критерий χ 2 работает при теоретической частоте классов ≥
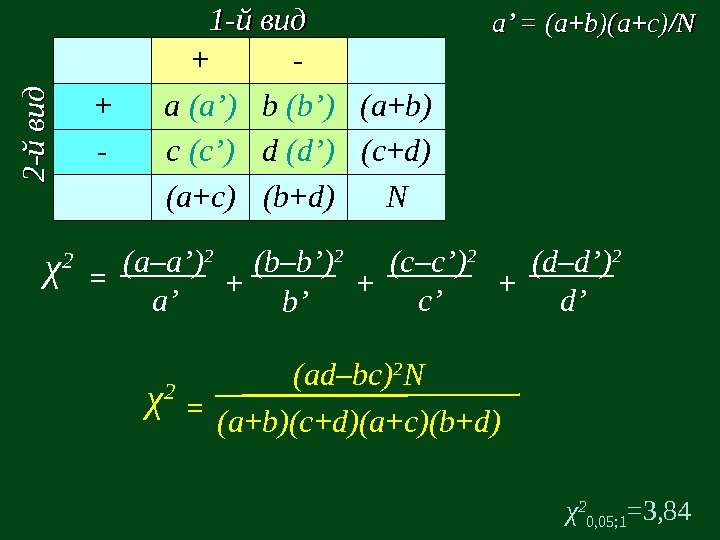 + — + a (a’) b (b’) (a + b) — c (c’) d (d’) (c + d) (a + c) (b + d) N 1 -1 — й вид 22 —й в и д a’ = (a ++ b)(a ++ c)c) // NN = (a–a’) 2 a’ (b–b’) 2 b’ (c–c’) 2 c’ (d–d’) 2 d’χ 2 +++ (ad–bc) 2 N (a + b)(c + d)(a + c)(b + d)=χ 2 0 , 05 ; 1 =3,
+ — + a (a’) b (b’) (a + b) — c (c’) d (d’) (c + d) (a + c) (b + d) N 1 -1 — й вид 22 —й в и д a’ = (a ++ b)(a ++ c)c) // NN = (a–a’) 2 a’ (b–b’) 2 b’ (c–c’) 2 c’ (d–d’) 2 d’χ 2 +++ (ad–bc) 2 N (a + b)(c + d)(a + c)(b + d)=χ 2 0 , 05 ; 1 =3,
 P + P- L + 20 13 L- 5 12 Pestalotiopsis submersis. L e m o n n ie ra te rre stris 33 17 5025 25 50 (ad–bc) 2 N (a + b)(c + d)(a + c)(b + d)=χ 2 ( 20 12 – 13 5 ) 2 50 33 17 25 25=χ 2 + — + a b (a + b) — c d (c + d) (a + c) (b + d) N = 4, 37 χ 2 0 , 05 ; 1 =3, 84 => отвергаем гипотезу о независимости встречаемости видов > 3,
P + P- L + 20 13 L- 5 12 Pestalotiopsis submersis. L e m o n n ie ra te rre stris 33 17 5025 25 50 (ad–bc) 2 N (a + b)(c + d)(a + c)(b + d)=χ 2 ( 20 12 – 13 5 ) 2 50 33 17 25 25=χ 2 + — + a b (a + b) — c d (c + d) (a + c) (b + d) N = 4, 37 χ 2 0 , 05 ; 1 =3, 84 => отвергаем гипотезу о независимости встречаемости видов > 3,
 P + P- L + 20 13 L- 5 12 Pestalotiopsis submersis. L e m o n n ie ra te rre stris 33 17 5025 25 50 + — + a b (a + b) — c d (c + d) (a + c) (b + d) N χ 2 0 , 05 ; 1 = 3, 84 χχ 22 K K == NN = 30% χ 2 = 4, 37 N = 50 adad –– bcbc (a(a ++ b)(c ++ d)(a ++ c)(b ++ d)d)==KK (ad – bc) 2 N (a + b)(c + d)(a + c)(b + d)=χ
P + P- L + 20 13 L- 5 12 Pestalotiopsis submersis. L e m o n n ie ra te rre stris 33 17 5025 25 50 + — + a b (a + b) — c d (c + d) (a + c) (b + d) N χ 2 0 , 05 ; 1 = 3, 84 χχ 22 K K == NN = 30% χ 2 = 4, 37 N = 50 adad –– bcbc (a(a ++ b)(c ++ d)(a ++ c)(b ++ d)d)==KK (ad – bc) 2 N (a + b)(c + d)(a + c)(b + d)=χ
 ad – bc (a + b)(c + d)(a + c)(b + d)=Kцентрированный, симметричный, абсолютный индекс межвидовой сопряженности Коэффициент сопряженности (редуцированный коэффициент корреляции); А + А — В + a b В — c d Плохо работает при сильно различной встречаемости видов.
ad – bc (a + b)(c + d)(a + c)(b + d)=Kцентрированный, симметричный, абсолютный индекс межвидовой сопряженности Коэффициент сопряженности (редуцированный коэффициент корреляции); А + А — В + a b В — c d Плохо работает при сильно различной встречаемости видов.
 Коэффициент Л. Коула – центрированный, несимметричный, полный индекс межвидовой сопряженности А + А — В + a b В — c d ad>bc ad d C= ad — bc ( a + b )( a + c ) C= ad — bc ( c + d )( b + d ) А + А — В + a b В — c db ≤c
Коэффициент Л. Коула – центрированный, несимметричный, полный индекс межвидовой сопряженности А + А — В + a b В — c d ad>bc ad d C= ad — bc ( a + b )( a + c ) C= ad — bc ( c + d )( b + d ) А + А — В + a b В — c db ≤c
 Коэффициент Л. Коула Вероятность встретить вид А: Р ( А +)=( a + c )/ N A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) N И вероятность встретить вид В: Р ( B +)=( a + b )/ N Если встречаемость этих двух видов независима, то вероятность обнаружить на учетной площадке оба этих вида: Р ( A +, B +)= [ ( a + c )/ N ] *[ ( a + b )/ N ] Тогда число учетных площадок, где обнаружены оба вида, будет равно: N* Р ( A +, B +)= N *[ ( a + c )/ N ] *[ ( a + b )/ N ]= ( a + c ) ( a + b ) N Но в действительности число учетных площадок, где обнаружены оба вида, равно a.
Коэффициент Л. Коула Вероятность встретить вид А: Р ( А +)=( a + c )/ N A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) N И вероятность встретить вид В: Р ( B +)=( a + b )/ N Если встречаемость этих двух видов независима, то вероятность обнаружить на учетной площадке оба этих вида: Р ( A +, B +)= [ ( a + c )/ N ] *[ ( a + b )/ N ] Тогда число учетных площадок, где обнаружены оба вида, будет равно: N* Р ( A +, B +)= N *[ ( a + c )/ N ] *[ ( a + b )/ N ]= ( a + c ) ( a + b ) N Но в действительности число учетных площадок, где обнаружены оба вида, равно a.
 Коэффициент Л. Коула A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) NОтклонение реального числа площадок, где обнаружены оба вида одновременно, от теоретического числа будет равно: a- = ( a + c ) ( a + b ) N a(a+b+c+d)- ( a + c ) ( a + b ) N a 2 +ab+ acac +ad-a 2 -ab-ac-bc N= ad-bc N= Если ( a+b )<( a + c ) , то максимально возможное число учетных площадок, где обнаружены оба вида, будет равно ( a+b ) и максимально возможное отклонение реального числа площадок, где обнаружены оба вида одновременно, от теоретического числа будет равно: ( a+b ) — ( a + c ) ( a + b ) N = ( a + b )( a+b+ cc +d-a-c ) N ( a + b )( b + d ) N=
Коэффициент Л. Коула A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) NОтклонение реального числа площадок, где обнаружены оба вида одновременно, от теоретического числа будет равно: a- = ( a + c ) ( a + b ) N a(a+b+c+d)- ( a + c ) ( a + b ) N a 2 +ab+ acac +ad-a 2 -ab-ac-bc N= ad-bc N= Если ( a+b )<( a + c ) , то максимально возможное число учетных площадок, где обнаружены оба вида, будет равно ( a+b ) и максимально возможное отклонение реального числа площадок, где обнаружены оба вида одновременно, от теоретического числа будет равно: ( a+b ) — ( a + c ) ( a + b ) N = ( a + b )( a+b+ cc +d-a-c ) N ( a + b )( b + d ) N=
 Коэффициент Л. Коула A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) N ( ad > bc; b <c) C= ad — bc ( a + b )( b + d )Реальное отклонение числа возможных встреч от теоретического Максимально возможное отклонение числа возможных встреч от теоретического = = ( ad-bc) / N [ ( a+b )( b + d )]/ N = Используют при низком β -разнообразии
Коэффициент Л. Коула A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) N ( ad > bc; b <c) C= ad — bc ( a + b )( b + d )Реальное отклонение числа возможных встреч от теоретического Максимально возможное отклонение числа возможных встреч от теоретического = = ( ad-bc) / N [ ( a+b )( b + d )]/ N = Используют при низком β -разнообразии
 ТКД – Коэффициент Л. Дайса трансформированный ( центрированный, несимметричный, полный индекс перекрытия ) χ 2 =( a + min ( b, c ))*TK Д 2 ТКД = a – min ( b, c ) a + min ( b, c ) Используют при высоком β -разнообразии A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) N
ТКД – Коэффициент Л. Дайса трансформированный ( центрированный, несимметричный, полный индекс перекрытия ) χ 2 =( a + min ( b, c ))*TK Д 2 ТКД = a – min ( b, c ) a + min ( b, c ) Используют при высоком β -разнообразии A+ A- B+ a b (a + b) B- c d (c + d) (a + c) (b + d) N
 + — + a b (a + b) — c d (c + d) (a + c) (b + d) N + — + 9 0 — 0 0), min( ))()()(( cba ТКД dbcadcba bcad K Все рассмотренные выше коэффициенты связи покажут 100%-ную связь.
+ — + a b (a + b) — c d (c + d) (a + c) (b + d) N + — + 9 0 — 0 0), min( ))()()(( cba ТКД dbcadcba bcad K Все рассмотренные выше коэффициенты связи покажут 100%-ную связь.
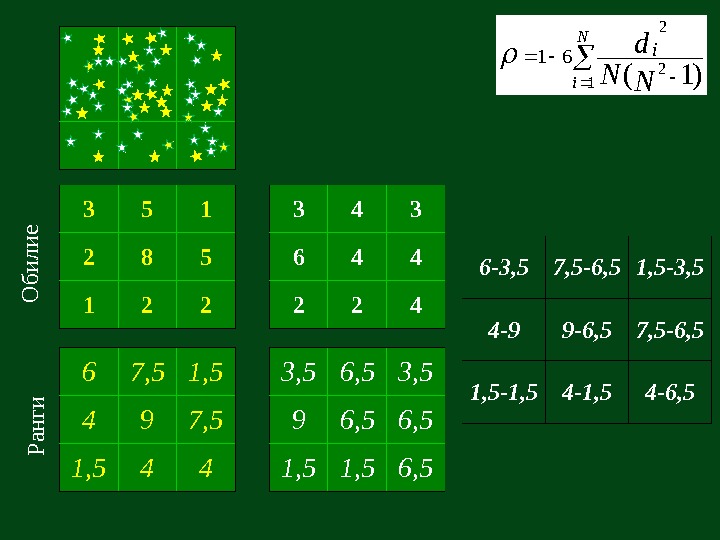
 Коэффициент Ч. Спирмена (коэффициент ранговой корреляции) – симметричный и центрированный коэффициент связи. ρ = 1 – 6 Σ d i 2 N ( N 2 -1)i = 1 N Разность рангов признаков сравниваемых видов на i — той площадке (признаком может служить как встречаемость, так и обилие вида) Общее число площадок
Коэффициент Ч. Спирмена (коэффициент ранговой корреляции) – симметричный и центрированный коэффициент связи. ρ = 1 – 6 Σ d i 2 N ( N 2 -1)i = 1 N Разность рангов признаков сравниваемых видов на i — той площадке (признаком может служить как встречаемость, так и обилие вида) Общее число площадок
 3 5 1 2 8 5 1 2 2 6 7, 5 1, 5 4 9 7, 5 1, 5 4 4 3 6 4 4 2 2 4 3, 5 6, 5 3, 5 9 6, 5 1, 5 6, 5 6 -3, 5 7, 5 -6, 5 1, 5 -3, 5 4 -9 9 -6, 5 7, 5 -6, 5 1, 5 -1, 5 4 -6, 5 О б и л и е Р а н ги N i NN d i 1 2 2 )1(
3 5 1 2 8 5 1 2 2 6 7, 5 1, 5 4 9 7, 5 1, 5 4 4 3 6 4 4 2 2 4 3, 5 6, 5 3, 5 9 6, 5 1, 5 6, 5 6 -3, 5 7, 5 -6, 5 1, 5 -3, 5 4 -9 9 -6, 5 7, 5 -6, 5 1, 5 -1, 5 4 -6, 5 О б и л и е Р а н ги N i NN d i 1 2 2 )1(
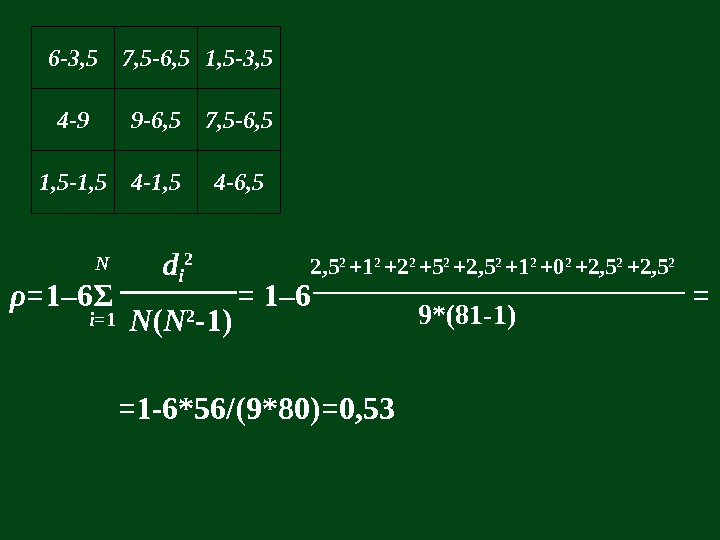 6 -3, 5 7, 5 -6, 5 1, 5 -3, 5 4 -9 9 -6, 5 7, 5 -6, 5 1, 5 -1, 5 4 -6, 5 ρ = 1– 6 Σ d i 2 N ( N 2 -1)i = 1 N = 1– 6 2, 5 2 +1 2 +2 2 +5 2 +2, 5 2 +1 2 +0 2 +2, 5 2 9*(81 -1) = = 1 -6*56/(9*80)=0,
6 -3, 5 7, 5 -6, 5 1, 5 -3, 5 4 -9 9 -6, 5 7, 5 -6, 5 1, 5 -1, 5 4 -6, 5 ρ = 1– 6 Σ d i 2 N ( N 2 -1)i = 1 N = 1– 6 2, 5 2 +1 2 +2 2 +5 2 +2, 5 2 +1 2 +0 2 +2, 5 2 9*(81 -1) = = 1 -6*56/(9*80)=0,


